基于前推回代法的含分布式電源配電網潮流計算

趙昱森

西安石油大學電子工程學院（陜西 西安 710065）

0 引言

在配電網中引入分布式電源（DG）后，配電網由單一電源轉變為多種電源系統，會對配電網的網損、電壓分布和電能質量產生影響。分析配電網在DG 接入后產生的影響，重要手段就是對含DG 的配電網進行潮流分析[1]。

文章在分析了各種DG 的并網特征后，介紹了DG 并網之后的簡化模型，將這些DG 等效為PI、PV、PQ 與PQ（V）節點。在使用前推回代法計算潮流時，由于計算方法的缺陷，對PV 節點的計算會失效。針對此種狀況，文章采用無功修正方程對節點進行無功修正[2]。

1 常見DG 在潮流計算中的模型

一般常見的含DG 的配電系統有分布式光伏發電、分布式風力發電以及燃料電池和微型燃氣輪機發電等[3]。在分布式光伏發電中，在使用電流逆變器時一般將其等效為PI 節點；在使用電壓逆變器時通常將其等效為PV節點。在分布式風力發電中，感應異步電機有恒速、恒頻的特性，可以看作具有電壓靜特性的PQ（V）節點，雙饋式電機一般則等效為PQ 節點。燃料電池通常在系統中等效為PV 節點；微型燃氣輪機則根據對勵磁控制方式的不同分為兩種，當控制勵磁方式為電壓控制時可以看作為PV 節點；當控制方式為功率因數時等效為PQ節點[4-10]。

2 改進的前推回代法潮流計算

2.1 PV 節點的無功修正計算

對于PV 節點的處理，文章采取對PV 節點進行無功功率修正的方法，取無功功率初值為：

式中：Qmax為無功功率的上限；Qmin為無功功率的下限。

設U0為PV 節點的額定電壓，則節點電壓的差值△U=U0-U。可得不同迭代次數的無功功率：

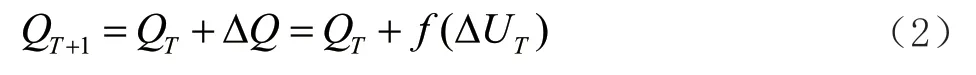
式中：T 為迭代次數；△Q 為無功功率的修正值。

當配電網絡的末端有n 個PV 節點時，設PV 節點處的節點阻抗矩陣為Z，有Z=R+jX ；設矩陣 ΔI˙為n 個PV節點電流變化量, 則PV 節點的電壓差值可以表示為：

由復功率的公式可以得到：

配電網中節點電壓的標幺值約等于1，所以可以得到：

將公式（5）代入公式（3）中，得到：

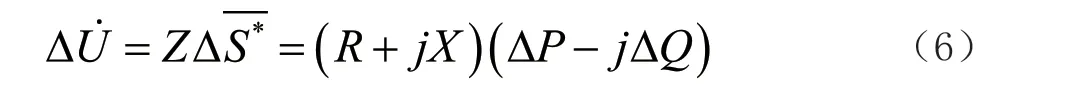
可以近似看成：

當節點類型為PV 節點時，△P=0，所以可以得到無功差值為：

2.2 PI 節點的無功修正計算

PI 節點通常為使用電流逆變器的分布式光伏發電和使用電流逆變器的微型燃氣輪機。修正節點的無功功率由注入電流值、有功功率及上一次迭代電壓值得出，如下：

式中：P 為節點注入的有功；fk以及ek為節點電壓在第k 次迭代的實部以及虛部；I 為注入電流值；QT+1為分布式電源在第k+1 次迭代的無功功率值。

2.3 PQ（V）節點的無功修正計算

感應異步電機具有恒速、恒頻的特性，因此可以看作具有電壓靜特性的PQ（V）節點。設各個符號意義表示如下：U 為發電機端電壓，kV；Is為定子電流，A；Ir為轉子電流，A；Im為勵磁電流，A；s 為轉差率；Re為機械負載等效電阻，Ω；Xσ為漏磁抗，Ω；Xm為勵磁電抗，Ω；R 為轉子電阻，Ω。可以推導功率因數角正切公式以及感應電機輸出電磁功率公式，分別為：

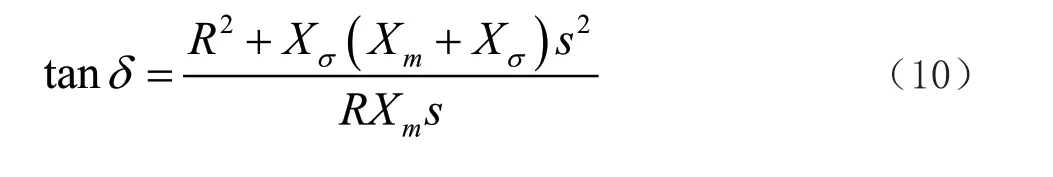
由此可以得出轉差率s 公式為：

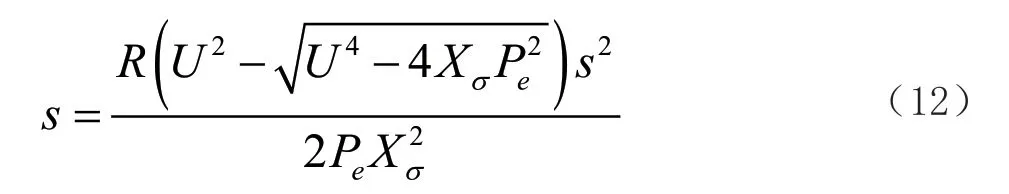
可以看出，PQ（V）節點的節點電壓會影響無功功率，節點發出的有功功率是定值，則該類型節點的無功修正方程表示為：

3 改進的前推回代法的步驟

（1）輸入配電網原始參數，確定配電網中DG 的位置以及節點類型。

（2）用參數計算網絡等值電抗矩陣。

（3）初始化各個節點的電壓初值、無功功率初值，PV 型節點的無功功率初值設為上下限的中間值，PQ（V）、PI 型節點的無功初值用上述公式計算。

（4）前推功率。從配電網絡的最后開始，對每條支路，用注入功率與阻抗數據推算各支路的電流與功率損耗，推算至根節點時停止。

（5）回代電壓。從根節點開始，以根節點的電壓與支路功率計算各個支路的節點電壓值，到線路末端停止。

（6）對PV 型節點的電壓進行收斂性判斷，判定條件如下：

式中：εpv為收斂精度；為該次計算得到的電壓幅值；Uschi為給定的初始節點電壓。若滿足條件進行第7 步，若不滿足則進行第8 步。

（7）判斷所有非PV 節點的電壓是否收斂，判斷條件為該次計算得出的電壓幅值上一次迭代得出的電壓幅值之差，取絕對值看是否滿足收斂精度。若不滿足收斂精度則進入第9 步，滿足條件進入最后一步。

（8）對PV 型節點的無功判斷是否越界，若無功沒有越界，則可以通過公式計算出無功修正功率，修正節點的無功功率。若無功越界，則將PV 節點轉化為PQ 節點。轉化之后，轉回第4 步。

（9）用潮流計算得到的該次節點電壓替換各個節點的電壓初值，轉回第4 步。

（10）計算結束，輸出結果。

4 算例驗證

為了測試上文所述的可行性，文章選取了IEEE33節點作為測試環境，如圖1 所示。該配電系統共有33個節點，系統的收斂精準度ε 為10-6，系統的基準電壓UB=12.66 kV，系統的基準功率SB為10 MVA。算例中所使用的四種DGS 的參數如表1 所示。

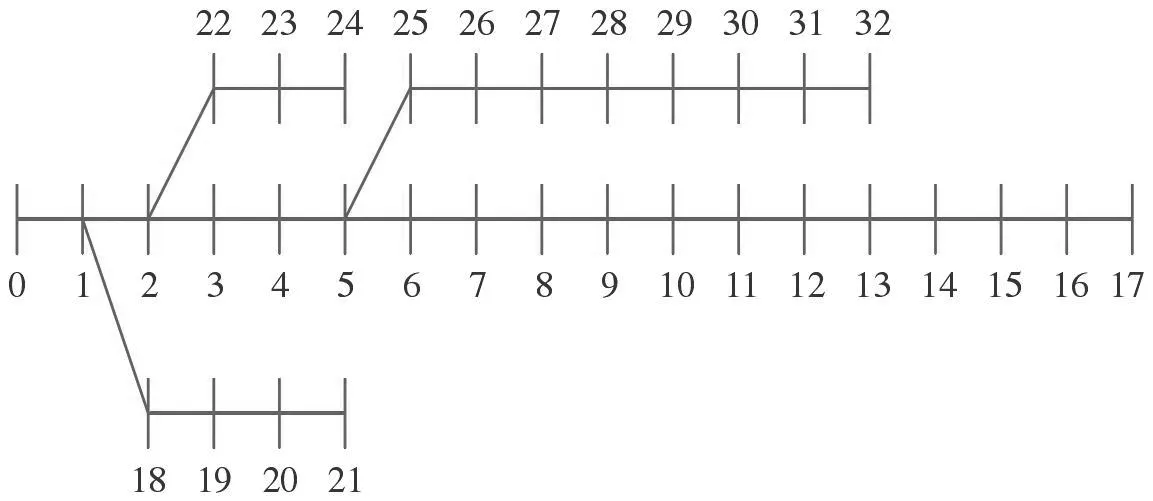
圖1 IEEE33 配電系統網絡拓撲結構

表1 四種DGS 的參數表

4.1 對算法正確性的驗證

為了驗證算法的正確性，實行對比實驗。

實驗1：在圖1 的配電系統中不接入DG，線路中均為PQ 節點，除根節點外。

實驗2：在節點號18、22、25、33 位置接入PQ 型DG。

實驗3 ～5：接入DG 的位置與實驗2 相同，接入DG類型分別為PI 型、PV 型、PQ（V）型DG。

用文章的算法分別計算以上方案，得到的電壓幅值曲線如圖2 所示。

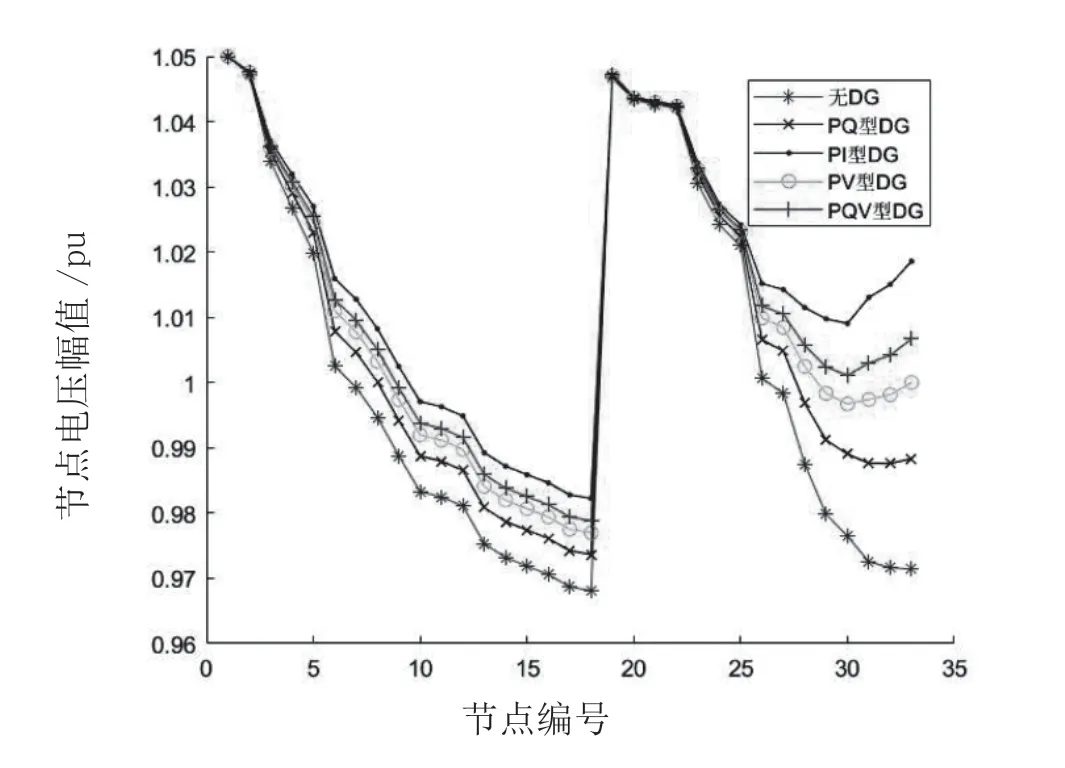
圖2 五種情況的電壓幅值曲線

由圖2 可知，五種情況計算得到的電壓幅值大體一致，證明文章算法適用于含DG 的配電系統潮流計算。

4.2 不同位置DG 對系統的影響

在同一系統中，分析DG 在不同位置時對潮流計算的影響。為了方便對比，對每種DG 類型設計了三種不同的位置情況。各種DG 接入位置以及迭代次數如表2所示。

從表2 可以看出，在潮流計算中DG 并網的位置對不同的節點類型影響也不同。對除PV 節點以外的節點而言，迭代計算的次數相差不大，幾乎相同。但是對PV 型節點而言，隨著PV 節點的增多，計算的迭代次數也隨之增大。因為隨著PV 節點的增多，需要不斷地進行無功修正計算，導致潮流計算的計算量較大。

5 結論

文章使用前推回代法分析研究了配電網在含有DG的情況下的潮流計算，對常見的幾種DG 進行了簡要分析，并且建立了相關數學模型。在IEEE33 節點配電系統中實行了算例仿真，經過分析得知：DG 的數量以及接入配電系統的位置會影響計算速度；文章運用該方法進行無功修正，在處理PV 節點時，較容易得出結果。

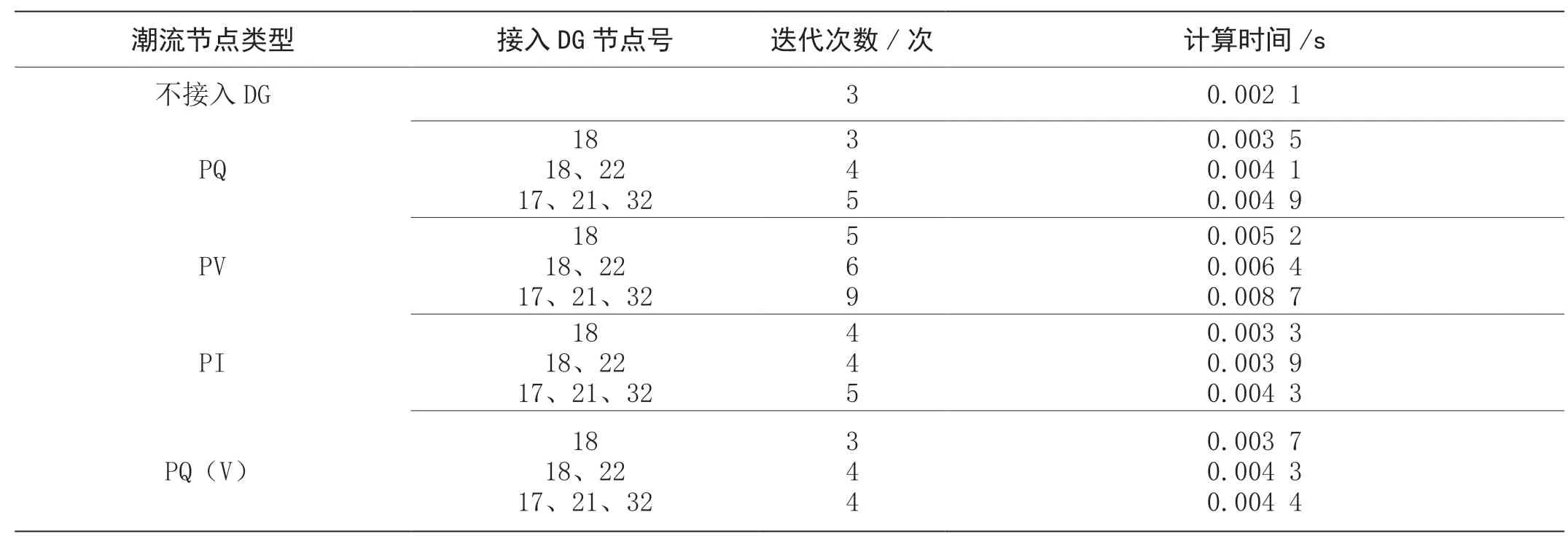
表2 各種DG 接入位置以及迭代次數