基于質量預測的飛機裝配動態調度問題研究

陸志強 朱宏偉 廖怡娜

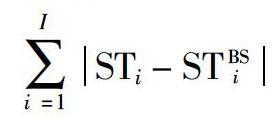
摘? ?要：為提高飛機裝配調度計劃應對裝配質量不合格的能力，首先以兩階段近似動態決策為框架，研究裝配質量與相關因素的映射關系和不確定性因素在不同決策周期的表現形式，并以最小化基于場景的項目工期期望值為目標函數建立整數規劃模型;然后基于構建的飛機裝配質量預測模型，設計了多層循環迭代搜索算法，算法第一層基于任務列表的編碼方式優化任務執行順序，第二層通過裝配人員分配列表優化人員配置，第三層根據人員配置結果求解目標函數. 數值實驗結果顯示在工件質量預測值與實際值不一致的情況下，多層循環迭代搜索算法在任務開始時間偏差能夠保持在2以下，表明該算法能夠適應不確定性因素的變化，滿足構建飛機裝配動態調度計劃的需求.

關鍵詞：飛機裝配;動態調度;人員配置;質量預測;多層循環迭代搜索算法

中圖分類號：F273? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Dynamic Scheduling Problem of Aircraft

Assembly Based on Quality Prediction

LU Zhiqiang?，ZHU Hongwei，LIAO Yina

（School of Mechanical and Energy Engineering，Tongji University，Shanghai 201804，China）

Abstract：To improve the ability of aircraft assembly schedule to deal with unqualified assembly quality，the mapping between assembly quality and quality-related factors and the expression of uncertainty in different decision-making cycles are studied，and the integer programming model is established with the objective function of the scenario-based project expected value. Moreover，based on the trained prediction model of aircraft assembly quality，a multi-layer cyclic iterative search algorithm is designed. The first layer optimizes the execution order of activity based on the activity list coding; The second layer optimizes the personnel allocation through the assembler allocation list; The third layer solves the objective function according to the result of personnel allocation. The numerical results show that the multi-layer cyclic iterative search algorithm can keep the deviation of activity start time below 2 when the predicted workpiece quality is inconsistent with the actual value，which indicates that it is adaptable to the changes of uncertainty factors and can meet the requirements of constructing dynamic schedules for aircraft assembly.

Key word：aircraft assembly;dynamic scheduling;personnel allocation;quality prediction;multi-layer iterative search algorithm

對飛機等大型設備裝配制造企業而言，建立合理的裝配調度計劃是有效提高裝配效率的途徑之一[1]. 許多因素影響著調度計劃的制定，包括各類資源供給限制、任務間的時序約束以及裝配過程中出現的各種不確定性因素等. 目前，已有學者對飛機裝配調度及相關衍生問題開展研究. 對于確定性問題，Lu[2]和朱宏偉[3]等認為飛機裝配過程主要涉及資源約束和任務順序關系兩類確定性約束，因此可以將飛機裝配調度問題抽象為資源受限項目調度問題（resource constrained project scheduling problem，RCPSP）及其擴展問題，并且可以通過構建啟發式或元啟發式算法[4-5]對問題進行有效求解. 在不確定性問題方面，現有研究主要涉及資源和任務相關的不確定性因素，包括物料到達不確定、任務工期不確定以及裝配質量缺陷等[6-8]. 其中，廖怡娜等[9]考慮任務因質量缺陷而導致的返工對計劃變動性的影響，以最小化項目工期與任務開始時間變動性為目標構建問題模型. 處理不確定性問題的方法主要包含反應式調度和前攝調度兩類，其中前攝調度通過添加時間或資源緩沖來提升前攝調度計劃的魯棒性，以預防不確定性事件導致的計劃中斷[10].

實際上，各質量相關因素對裝配或加工質量的影響以質量偏差傳遞過程的形式體現，而兩者的映射關系可以通過質量預測模型來建立. 賈峰等[11]采用復雜網絡建模理論構建葉片加工誤差傳遞網絡，以說明誤差在加工特征和工況要素間的傳遞過程. 王秋明等[12]通過灰色理論和反向傳播神經網絡實現各工序的質量預測. 鞠萍華等[13]提出一種基于GRA和AHP的廣義回歸神經網絡零件失效概率預測方法.

飛機裝配周期長，與資源、任務相關的不確定性因素隨著裝配進程的推進不斷變化，因此實際管理上更適合采用周期性的決策框架構建調度計劃，其中包括滾動時域法. Lee等[14]以滾動時域為框架解決短期調度問題. 張潔等[15]針對工時不確定的混合流水車間動態調度問題，提出基于交貨期偏差容忍度的滾動時域框架.

綜觀現有研究發現，現有調度方法往往在不確定性事件發生后進行被動處理且僅利用決策初期的信息，從而忽略了主動改善的優勢，同時也無法有效應對裝配過程中不確定因素不斷改變的情況.現有文獻雖然已經對質量偏差傳遞機理和預測方法進行了詳細的分析，但實際上，裝配人員的技能水平在很大程度上影響著飛機裝配的可靠性與穩定性，是產生質量缺陷的重要原因之一[16]，因此現有研究與真實的飛機裝配質量傳遞過程仍存在偏差. 滾動時域法則僅利用各決策點上的確定性信息，沒有充分考慮到不確定性因素對計劃構建的影響，而韓笑樂等[17]提出基于兩階段近似的動態決策框架能夠充分利用未來不確定性場景來輔助評價當前決策優劣，提升調度計劃應對未來不確定性因素的能力.

針對上述不足，本文分析了包括裝配人員技能水平在內的質量因素對任務裝配質量影響情況，建立飛機裝配質量映射關系和預測模型;以此為基礎，結合兩階段近似的動態決策框架，研究包括工件質量在內的不確定性因素對當前決策周期飛機裝配調度計劃構建的影響形式，建立基于不確定性場景的混合整數規劃模型;最后，針對問題多階段的特性，以禁忌搜索為框架構建多層循環迭代搜索算法進行求解.

1? ?問題描述及數學模型

1.1? ?問題描述

飛機裝配涉及的零部件多種多樣、數量龐大且工藝復雜，裝配任務的完工質量是否能夠達到規定標準除了與當前任務的待裝配零部件質量、前序任務的完工質量有關以外，裝配人員的技能水平也是影響質量的重要因素之一[13]，因此，在本文的研究中，將裝配人員技能水平l作為影響任務質量的主要因素之一，使其與待裝配零部件質量Qpart、前序任務完工質量Qpre一同決定各飛機裝配任務的完工質量，并以此為基礎對裝配項目進行調度.

由于飛機裝配周期較長，因此在實際的裝配項目中，裝配中心往往需要對供應鏈上的一系列因素，包括倉庫的存儲能力及費用、訂貨費用和訂貨次數等進行綜合考量，制定合理的零部件采購計劃，使得待裝配零部件按照一定時間從供應商處分批次運送至裝配中心進行加工制造，因此裝配項目中各任務的待裝配零部件質量狀況通常無法在項目開始前全部知曉，而是隨著裝配項目的推進逐漸明確、又基于前文可知，待裝配零部件質量Qpart是影響各裝配任務完工質量的主要因素之一，因而裝配項目中各任務的實際裝配質量將隨著待裝配零部件質量的已知進而確定.

韓笑樂等[17]基于船舶調度背景提出的集裝箱進出口碼頭泊位-堆場協同分配的動態決策問題與本文研究問題具有諸多共性：首先從目標來說，兩者均是在特定背景下試圖得到較優的調度結果;其次，兩者均具備進行周期劃分的條件，前者假設每一周期內部分船舶的確切到港時間可提前已知，后者則基于實際情況假設各裝配任務的待裝配零部件分批次到達，零部件到達后其質量情況才能夠已知;然后在調度因素方面，前者需要對碼頭和堆場資源進行協同決策，后者則需要對裝配任務的開始時間、包括裝配人員在內的可更新資源進行聯合分配;最后，后續不確定性場景均對兩者的調度計劃產生影響，對前者則影響整體調度計劃中的船舶在港總時間，對后者則影響整體調度計劃的項目工期. 基于上述共性，參考韓笑樂等[17]提出的兩階段近似的動態決策框架，對本文研究問題進行抽象.

綜合上述分析，本文在兩階段近似動態決策框架的基礎上，將任務質量引入調度決策中，考慮后續不確定性場景對整體調度計劃的影響，得到滾動時域框架下基于任務質量預測的飛機裝配動態調度問題，該問題具體描述如下.

裝配項目J中包含n個裝配任務i∈J和m種資源k∈K;任務的工期為d，與任務的完工質量有關，將在后文中詳述;單位時間內消耗各類資源量為r，每種資源任意時刻供給上限記為R;各任務之間存在時序關系，任務一旦開始就不允許中斷. 將整個裝配過程分成多個階段進行決策，同時裝配任務可以根據其零部件質量狀況Qpart在決策時間點處是否已知進行區分. 對于在決策時間點處零部件質量未知的任務，其零部件質量狀況存在多種不同情況，可表示為多個不確定性場景. 如圖1所示，在飛機裝配動態決策問題中，在任一決策點對任務進行調度時可分為兩個階段，第一階段是對當前決策階段中的各個任務進行安排，為固定性決策;第二階段是對后續決策階段的各個任務進行安排，為調整決策. 由于后續決策階段中存在多個不確定性場景，因此調整決策為臨時的，僅用于輔助評估第一階段的固定性決策. 固定決策階段和調整決策階段分別針對不同的任務進行調度，在任一決策時間點，可將各任務分為A、B、C 3類，對于不同類別的任務，將其歸于上述不同的決策階段. 各類任務分類信息及其與不同決策階段之間的關系如下：

1）已開始任務（A類任務）. 對于該類任務，已知的確定參數包括：任務執行時間dA、裝配人員需求rA、工件質量情況Qpart，A、任務開始時間xA和裝配人員分配情況yA. 該類任務無不確定參數，無需決策，僅需按照事先制定的計劃完成剩余任務即可.

2）可在當前決策周期內開始執行的任務（B類任務）. 已知的確定參數包括：裝配人員需求情況rB和工件質量情況Qpart，B. 可根據是否延遲到當前周期后執行而分為B0類和B1類任務. 對于B0類任務需進行第一階段的固定性決策，包括為其分配具體的任務開始時間xB0和裝配人員分配情況yB0，并通過裝配質量映射關系間接確定其任務執行時間工期dB0. 對于B1類任務，由于其保留在下一周期再次決策的機會，因此進行第二階段的調整性決策，具體決策過程與C類任務相似.

3）在當前決策周期k后開始執行的任務（C類任務）. 已知的確定參數為裝配人員需求情況rC，不確定參數為各場景下的工件質量情況Qpart，C

m? ? ? ? ?. 此時需要進行第二階段各場景下的調整決策，包括與場景相關的任務開始時間xC

m和裝配人員分配情況yC

m. 調整決策在決策點k+1處仍有進一步調整的機會.

如前文所述，任意裝配任務i的完工質量由3個因素決定，分別為裝配人員技能水平l、待裝配零部件質量Qpart以及前序相關任務完工質量Qpre. 其中，由于任務間的時序約束以及傳遞耦合效應，使得當前裝配任務i的裝配質量受到前序相關任務的完工質量Qpre的影響，同時質量情況也通過任務時序網絡進行傳遞，任務完工質量傳遞關系如圖2所示. 為了提升算法搜索效率，對研究問題進行了簡化，對于裝配人員技能水平因素，當前裝配任務i所配備的裝配人員集合中具備最高技能水平的裝配人員對任務質量起主要作用，并將所配備的最高技能水平記為lmax . 另外，在實際情況下，由于飛機裝配質量的傳遞過程具有高度非線性，任務完工質量和影響質量狀況的因素之間的具體關系通常不存在顯式表達，在本文中，將通過SVR機器學習模型結合上述3種影響因素對各任務完工質量進行預測，因此，任意任務的完工質量與3種影響因素之間的映射關系表示為Q = f（lmax，Qpart，Qpre）.

裝配任務的質量情況是本文研究問題中影響調度計劃的不確定性因素，其對調度計劃的影響在于裝配質量的不合格會引起任務工期d的變化，具體而言，若裝配任務完工質量合格，則其實際工期僅為提前已知的正常執行工期，即d = dflxed;若裝配任務完工質量不合格，為了保證其后續任務的質量，需要對當前質量不合格的裝配任務進行返工，表現為在原本正常執行工期的基礎上添加一段返工工期drework，此時，當前任務的實際工期為d = dflxed + drework. 又基于上述任務完工質量Q是由所配備的裝配人員具有的最高技能水平lmax、待裝配零部件質量狀況Qpart和前序相關任務完工質量Qpre 3因素決定的，故任務實際工期d與這3種質量影響因素之間的關系可表示為d = F（lmax，Qpart，Qpre）.

1.2? ?數學模型

參數：

Cm：場景[ω] 中的裝配項目工期;

i∈I = {1，…，I }：裝配人員集合;

r∈R = {1，…，R}：資源集合，其中裝配人員集合為資源集合的子集，即M?R;

k∈K = {1，…，K}：資源種類集合;

l∈L = {1，…，L}：裝配人員水平集合;

t∈T = {1，…，T}：離散化的時間段集合;

[ω] ∈Ω = {1，…，Ω}：場景集合;

Pi：任務i的緊前任務集合;

di：場景[ω] 中任務i的實際裝配時間;

IA，IB，IC：3類任務的子集合;

Qpart

i? ? ：任務i待安裝零部件質量;

Qpre

i? ? ：影響任務i質量的前道任務質量.

決策變量：

xit，ω：場景[ω] 中，若任務i在t時刻開始則取1，否則取0;

yim，ω：場景[ω] 中，若把裝配人員m分配給任務i則取1，否則取0;

ui：若任務i∈IB且任務被延遲至周期k之后開始執行則取1，否則=0.

模型：

其中目標函數（1）為最小化決策點時各場景下的項目工期期望值;約束（2）確保任一任務的開始時間不早于其前序任務的結束時間;約束（3）為資源約束;約束（4）代表任務開始后不允許中斷;約束（5）限制任意裝配人員在某時刻最多操作一個任務;由于飛機裝配傳遞過程的高度非線性導致裝配質量和影響其的3個因素之間的具體關系未知，因此通過約束（6）（7）表示裝配質量、任務實際工期與人員水平、工件質量及緊前任務質量間的映射關系，裝配任務的完工質量將通過預測模型實現;約束（8）～（14） 確保各類別任務在不同場景下決策的一致性;（15）～（17）代表了決策變量的取值范圍.

2? ?算法描述

為適用飛機裝配動態決策問題存在多階段決策的情況，本文依據問題模型特點和決策邏輯，提出多層循環迭代搜索算法. 算法主要思路為：結合裝配任務歷史質量數據，以裝配質量相關參數為輸入、裝配質量為輸出，構建飛機裝配質量預測模型. 以飛機裝配質量預測模型為基礎，構建多層循環迭代搜索算法. 算法第一層基于任務列表的編碼方式，以禁忌搜索算法為框架優化任務執行順序;第二層通過設計裝配人員分配列表的編碼方式完成第一階段固定性決策;第三層仍采用任務列表編碼方式搜索第二階段調整性決策，并通過計算各場景下的項目工期均值來評價整體決策的優劣性. 具體步驟在2.1節和2.2節中詳細闡述.

2.1? ?飛機裝配質量預測模型

如第1節中所描述，飛機裝配質量受到包括裝配人員分配情況、工件質量等多方面因素綜合的影響，因此需要構建有效的預測模型來準確描述裝配質量傳遞效應. 考慮到飛機質量傳遞過程具有高度的非線性[18]以及支持向量回歸（SVR）在非線性預測領域的適用性[19]，本文采用支持向量回歸（SVR）構建飛機裝配質量預測模型.

基于前文分析，任務質量狀況由該任務所配備裝配人員具備的最高技能水平lmax、待裝配零部件質量情況Qpart以及前序相關任務質量狀況Qpre決定，因此將該3種質量影響因素作為質量預測模型的輸入，當前任務完工質量狀況作為質量模型的輸出構建質量預測模型樣本，進而建立用于裝配任務完工質量預測的SVR支持向量回歸模型. 質量預測模型樣本構成具體為：對于任意任務i，記樣本為Si = {（Xim，Yim）}（其中m = 1，…，M為編號索引）. 其中Xim = {lmax，Qpre

i? ? ，Qpart

i? ? ?}為輸入向量，lmax表示任務i所分配裝配人員的最高水平，Qpart

i? ? ?= {dpart

i? ? ?，spart

i? ? ?，opart

i? ? ?} 表示裝配任務所需工件的公稱要求、公差和實際誤差，Qpre

i? ? = {Δxj1，Δyj1，Δzj1，…，Δxjn，Δyjn，Δzjn}表示對當前任務具有最大影響的緊前任務j在檢測點1 ～ n上測量所得相對于名義坐標的偏差;Yim = {Δxi1，Δyi1，Δzi1，…，Δxin，Δyin，Δzin}為輸出向量，表示實際情況下任務i以Xim為質量傳遞輸入時在檢測點1 ～ n上測量所得相對于名義坐標的偏差.

SVR的基本原理為根據給定的訓練數據集在高維特征空間中尋求一個最優超平面，使得所有樣本點離超平面的總方差不大于預先給定的誤差. 此外，為適用飛機裝配質量為多個輸出值的情況，本文引入多輸出回歸，將原來的多輸入多輸出樣本集合（Xim，Yim）拆分為3n個多輸入單輸出的子樣本集合（Xim，Δxi1），（Xim，Δyi1），…，（Xim，Δzin），通過SVR模型對這些子樣本集合的學習，分別得到各單一輸出對應輸入特征向量的3n個超平面. 最后通過測試樣本對訓練所得SVR模型進行預測準確性的檢測. 飛機裝配質量預測模型訓練及預測過程可由圖3表示.

2.2? ?多層循環迭代搜索算法

不同于以往飛機調度問題決策過程，以下兩類特點使得本問題的決策難度顯著提升：不同裝配人員之間的水平分級使得本問題在保留以往飛機調度問題中所涉及的時間決策的基礎上，進一步耦合了資源決策需求;于此同時，相較于單場景模型，基于場景的混合整數規劃模型進一步擴大了各決策時間點上的決策規模. 因此，本文采用多層循環迭代搜索算法在各決策時間點上構建裝配計劃. 其中，鑒于禁忌搜索算法在鄰域搜索及求解效率的優勢，多層循環迭代搜索算法各層均采用禁忌搜索算法作為算法框架. 具體而言，算法第一層（TS1）借鑒陸志強等[20]所采用的任務列表編碼方式對任務執行順序展開搜索;算法第二層（TS2）采用裝配人員分配編碼方式構建人員分配搜索模塊，搜索可能的人員配置情形，并在此基礎上通過串行調度算法區分B0、B1和C類任務;算法第三層（TS3）基于TS2任務區分的基礎上，在各場景下搜索較優調度計劃，計算調度計劃的評價指標. 多層循環迭代搜索算法框架如圖4所示.

計算各場景的評價目標均值作為

L2′評價目標值輸出][串行調度解碼，選擇最小工期

作為場景θ評價目標值][獲得L1′評價目標值][選擇具有最優評價目標值的L1*∈N（Lk）][基于任務列表編碼禁忌搜索算法（TS1）][初始化優先級列表L1][基于人員分配編碼禁忌搜索算法（TS2）][是][否][生成鄰域N（L1）][選擇L′

2.2.1? ?TS1：基于任務列表編碼禁忌搜索算法

任務列表編碼用于算法第一層TS1中的任務執行順序決策. 任務列表編碼包括A類任務和B、C類任務兩類任務集合，圖5（a）給出編碼的示例. 其中，每一編碼位的數字代表任務編號，編碼過程要求：1）虛擬開始任務和虛擬結束任務分別放入最開始的碼位和最后的碼位;2）后一碼位中的任務與前一碼位中的任務不能為直接或間接緊前關系;3）由于A類船無需決策，因此A類船置于列表中最高的優先級位置;4）B、C類任務具有等效的優先程度，因此在任務列表中混編. 初始任務列表由隨機規則產生.

TS1中禁忌搜索算法的鄰域通過選取編碼中兩個B、C類任務并對其進行單項互換操作來實現，其主要過程包括：從當前任務列表的B、C類任務中隨機選取兩個不存在直接或間接緊前關系的任務，對兩任務在列表中的位置進行互換. 圖5（b）給出單項互換操作的示例. TS1每一階段的禁忌對象為通過TS2和TS3解碼后評價指標最優的任務列表所對應的單項互換操作. 設置禁忌搜索算法的最大循環次數為iter1，禁忌次數在上限tabumax

1? ? ?和下限tabumin

1? ? ?間隨機生成.

2.2.2? ?TS2：基于人員分配編碼禁忌搜索算法

不同的人員分配方案不僅會影響任務執行時間，同時也會間接的影響B0、B1和C類任務的劃分情況. 因此，本文設計人員分配編碼用于人員分配方案的決策. 初始人員分配編碼通過最高人員水平（highest quality level，HQL）規則生成. 采用HQL規則時，待安排任務會被分配剩余裝配人員集合中裝配水平最高的人員. 人員分配編碼過程為：從待調整的任務集合中隨機選取待調整任務組合 （i，j），其中必須保證任務i、 j之間不存在緊前關系且兩任務的開始和結束時間滿足STi < STj < FTi或STj < STi < FTj（如圖6（a）所示）.

鄰域生成通過對待調整任務組合（i，j）間的裝配人員交換操作實現，其中考慮到潛在的人員交換操作有很多，因此本文僅考慮任務組合（i，j）的最高水平裝配人員M *交換操作，即R′

i. TS2每一階段的禁忌對象為通過TS3解碼后最優評價指標所對應的人員交換操作. 設置禁忌搜索算法的最大循環次數為iter2，禁忌次數在上限tabumax

2? ? ?和下限tabumin

2? ? ?間隨機生成.

2.2.3? ?TS3：基于任務列表編碼評價目標生成算法

評價目標的生成算法同樣采用任務列表為編碼方式，使用HQL規則生成人員分配方案. 在由TS1所構建的任務列表和TS2所構建的人員分配列表生成最終評價目標時，基于任務列表編碼評價目標生成算法首先對在各場景ω下由B1和C類船構成的部分列表進行單項互換操作，然后采用基于HQL規則的串行調度算法求解該場景下的較優項目工期，最后通過求解所有場景下的項目工期期望來獲得評價目標.

TS3中單項互換操作與TS1中類似，各場景ω下的禁忌對象為上一步移動的互換操作. 設置禁忌搜索算法的最大循環次數為iter3，禁忌次數在上限tabumax

3? ? ?和下限tabumin

3? ? ?間隨機生成.

3? ?數值實驗

3.1? ?測試環境

為驗證所提決策框架的有效性，以某型號支線客機前機身、后機身和機身尾軸裝配工位的部分裝配流程和歷史裝配數據構建實驗算例. 上述裝配流程所包含裝配任務數量分別為21、32和42項，所構建算例分別記為C21、C32和C42. 裝配過程所涉及裝配人員的技能水平可劃分為高級、中級和初級3種. 上述質量預測模型和各對比算法均通過python3.7編程實現，數值實驗在Internet Core i7處理器，3.4 GHz主頻，16 G內存的計算平臺上進行.

3.2? ?飛機裝配質量預測模型效果驗證

從上述C21、C32和C42 3類算例中選取裝配任務的歷史裝配質量信息構建預測模型訓練樣本和測試樣本，并通過交叉驗證法對比裝配質量預測值與實際值間的偏差，以驗證飛機裝配質量預測模型的準確性. 模型訓練過程為每一道任務（除去虛擬任務）生成M = 1 000組訓練樣本Si = {（Xim，Yim）|?i∈I，m =1，2，…，M }，并按照圖2中的步驟訓練SVR模型. 選取5折為交叉驗證法折數. 此外，為進一步說明SVR預測的適應性，將SVR與BP神經網絡[21]預測準確率進行對比.

預測準確率均值如表1所示. 在所有算例中，SVR在任意技能水平所對應裝配質量預測準確率經交叉驗證后可以達到95%以上，遠優于BP神經網絡的預測準確率. 可以看出，本文所構建的飛機裝配質量預測模型能夠比較準確地根據質量輸入信息對任務裝配質量進行預測.

3.3? ?多層循環迭代搜索算法效果驗證

為了驗證周期性決策框架的適用性以及多層循環迭代搜索算法（記為TSM）的有效性，本文采用預設的質量分布參數構建實際工件質量場景，并提出另外3種調度計劃生成算法作為對照，對比各調度計劃生成算法所建調度計劃應對隨機擾動的能力. 設多層循環迭代搜索算法的決策周期跨度p = 10. 其他3種調度計劃生成算法均采用非動態決策框架，即在決策初期為所有任務構建模板調度計劃，且在實際裝配過程中不進行更改. 各算法具體構建方式如下.

CPLEX-RANDOM：首先在不考慮任務返工的情況下通過CPLEX軟件求解各算例，在保留CPLEX軟件所得最優模板計劃的任務執行順序的基礎上，為裝配任務隨機安排裝配人員，并通過飛機裝配質量預測模型重新確定任務執行時間.

CPLEX-TS：在CPLEX-RANDOM基礎上，通過增加基于人員分配編碼禁忌搜索算法（TS2）優化人員配置.

TSD：雙層循環迭代算法，其中上層采用基于任務列表編碼禁忌搜索算法（TS1），下層在基于人員分配編碼禁忌搜索算法（TS2）的基礎上進行改編，即通過串行調度算法構建模板調度計劃.

本文為C21、C32、C42 3個算例各生成c = 5組實驗，每組實驗隨機擾動次數設為50次. 在構建工件質量場景時，每組實驗中任務i的工件質量服從正態分布N（ETAsi，σsi|?s，?i）. 在評價模板調度計劃應對隨機擾動的能力時，本文采用右移算法（Right Shift）修復隨機擾動對模板計劃產生的影響. 右移算法作為常見的修復規則，其在保留原有任務執行順序的同時將受影響任務的開始時間依次順延. 采用右移算法時采取的評價指標包含項目實際工期和任務開始時間偏差. 其中，任務開始時間偏差表示為所有任務實際開始時間STi與模板計劃開始時間ST BS

i的偏差絕對值之和：

STi - ST BS

i

3.3.1? ?實驗1：工件質量預測值與實際值一致的情況

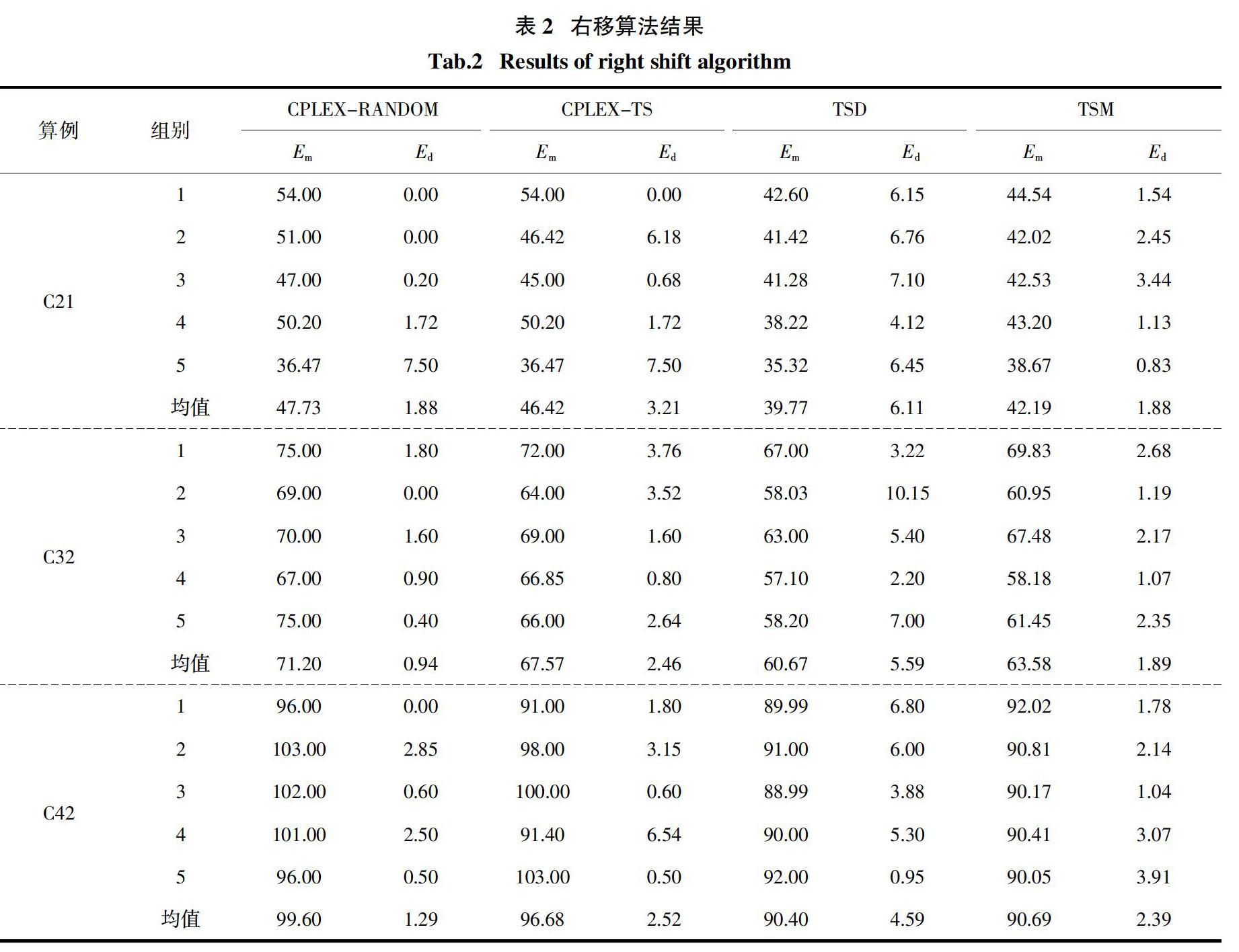
在該實驗中，考慮工件質量的預測值與實際值一致的情況，即決策初期預估的工件質量分布在項目執行過程中不發生改變. 各算法在隨機環境下右移算法所得結果如表2所示. 其中Em表示右移算法所得項目實際工期;Ed表示右移算法所得任務開始時間偏差.

由表2可以看出，在項目實際工期方面，TSD經右移算法所得平均實際執行工期依次優于CPLEX-TS和CPLEX-RANDOM，其原因包含兩方面：首先，基于人員分配編碼禁忌搜索算法（TS2）能夠實現人員分配的優化，從而減少任務因人員分配不合理而導致返工的情況發生;其次，通過基于任務列表編碼禁忌搜索算法（TS1）對任務執行順序實現優化，從而進一步降低任務延期對實際項目工期的影響. 此外，多層循環迭代搜索算法所得平均實際執行工期優于CPLEX-TS而較劣于TSD，其主要原因在于TSD為單次決策，即在決策點為所有任務構建的鄰域，其搜索范圍要大于多層循環迭代搜索算法.

在偏差方面，多層循環迭代搜索算法求得的計劃能夠取得最優或較優的任務開始時間偏差值. 在多數情況下，CPLEX-RANDOM雖然能夠取得最優任務開始時間偏差值，但這一結果是CPLEX-RANDOM犧牲項目工期評價指標而為任務設置大量時間緩沖所致. 多層循環迭代搜索算法所得平均最優計劃偏差值雖劣于CPLEX-RANDOM，但該算法能兼顧模板調度計劃在項目實際工期和任務開始時間偏差的綜合表現. 在3種規模算例下，多層循環迭代搜索算法所得項目實際工期和任務開始時間偏差均優于CPLEX-TS.

3.3.2? ?實驗2：工件質量預測值與實際值不一致的

情況

在該實驗中，考慮工件質量的預測值與實際值不一致的情況，即在項目執行過程中工件質量分布 N2（ETAsi，σsi）與決策初期預估的工件質量分布N1（ETAsi，σsi）不同. 在此情形下各算法所得結果如表3所示.

由表3可以看出，在工件質量的預測值與實際值不一致的情況下，各算法所得項目實際工期和任務開始時間偏差與實驗1中具有相同的規律：TSD能夠取得最優的平均項目實際工期，多層循環迭代搜索算法次之，而CPLEX-RANDOM所得平均項目實際工期最劣;在任務開始時間偏差方面，多層循環迭代搜索算法依舊能夠取得較優的表現，而TSD所得平均任務開始時間偏差最劣. 然而，比較表2和表3，能夠發現各算法雖然在項目實際工期方面變化不大（均值保持在1以內），但不同算法在任務開始時間偏差方面的變化情況不同，因此需要進一步分析.

圖7給出各算法分別在工件質量預測值與實際值一致與不一致情況下，任務開始時間偏差的變化情況（即表2和表3中Em和Ed的差值）. 能夠發現，在所有規模算例下，CPLEX-RANDOM、CPLEX-TS和多層循環迭代搜索算法在任務開始時間偏差變化均較小，能夠保持在2以下，而TSD的任務開始時間偏差變化在C21和C32算例中均為最大，且3個算例中均超多層循環迭代搜索算法. 上述情況的主要原因在于：CPLEX-RANDOM和CPLEX-TS在構建模板計劃時為任務設置大量時間緩沖，因此其模板計劃魯棒性較大，但也導致平均項目工期增大;TSD以工件質量的預測值構建模板計劃，因此在工件質量的實際值與預測值不一致的情況下，其任務開始時間偏差的變化較大;多層循環迭代搜索算法利用兩階段近似動態決策框架的優勢，在每一決策周期保留了調整模板計劃的機會，且基于場景的決策目標也使得計劃的調整以不確定性信息的變化情況為依據.

4? ?結? ?論

1）本文以飛機裝配質量映射關系和預測模型為基礎，研究包括工件質量在內的不確定性因素對飛機裝配調度計劃構建的影響形式，建立飛機裝配過程的兩階段近似動態調度模型. 其中動態調度模型以基于不確定性場景的項目工期期望為優化目標.

2）針對該問題耦合了時間決策與資源決策，且

因涉及不確定性場景而導致搜索規模增大的情況，提出了多階段循環迭代搜索算法. 算法第一層對任務列表進行搜索，以獲得較優的任務執行順序;算法第二層基于人員分配編碼對人員分配方案進行搜索，實現人員配置的優化;算法第三層通過搜索剩余任務所組成的任務列表，確保評價指標的有效性.

3）數值實驗結果表明多階段循環迭代搜索算法在不確定性環境中具有良好的求解性能，同時能夠有效應對不確定性因素在飛機裝配過程中的變化，驗證了該算法的有效性和可行性.

4）未來可以進一步研究設備狀態、設備維護計劃與飛機動態調度計劃的相互影響情況.

參考文獻

[1]? ? BROWNING T，YASSINE A. Resource-constrained multi-project scheduling：priority rule performance revisited[J]. International Journal of Production Economics，2010，126（2）：212—228.

[2]? ? LU Z，REN Y，WANG L，et al. A resource investment problem based on project splitting with time windows for aircraft moving assembly line[J]. Computers & Industrial Engineering，2019，135（1）：568—581.

[3]? ? 朱宏偉，陸志強. 考慮資源轉移時間的項目可拆分資源受限多項目調度問題[J]. 計算機集成制造系統，2019，25（3）：586—597.

ZHU H W，LU Z Q. Modeling and improved algorithm for resource constrained multi- project scheduling problem based on project splitting with resource transfer time[J]. Computer Integrated Manufacturing Systems，2019，25（3）：586—597. （In Chinese）

[4]? ? ZAMANI R. A competitive magnet-based genetic algorithm for solving the resource-constrained project scheduling problem[J]. European Journal of Operational Research，2013，229（2）：552—559.

[5]? ? CHEN R. Particle swarm optimization with justification and designed mechanisms for resource- constrained project scheduling problem[J]. Expert Systems with Applications，2011，38（6）：7102—7111.

[6]? ? 盧輝，王紅衛，李鋒，等. 考慮供應不確定性與需求非平穩性的項目調度與材料供應集成優化[J]. 系統工程理論與實踐，2019，39（3）：647—658.

LU H，WANG H W，LI F，et al. Integrated scheduling and material supply planning under nonstationary stochastic demand and random supply yield[J]. Systems Engineering-Theory & Practice，2019，39（3）：647—658. （In Chinese）

[7]? ? GUTJAHR W. Bi-objective multi-mode project scheduling under risk aversion[J]. European Journal of Operational Research，2015，246（2）：421—434.

[8]? ?MAGHSOUDLOU H，AFSHAR-NADJAFI B，NIAKI S. Multi-skilled project scheduling with level-dependent rework risk;three multi-objective mechanisms based on cuckoo search[J]. Applied Soft Computing，2017，54（1）：46—61.

[9]? ? 廖怡娜，陸志強. 考慮作業返工的資源受限項目調度問題[J]. 計算機集成制造系統，2019，25（11）：2762—2774.

LIAO Y N，LU Z Q. Resource-constrained project scheduling problem with reworking[J]. Computer Integrated Manufacturing Systems，2019，25（11）：2762—2774. （In Chinese）

[10]? 崔南方，趙雁，胡雪君. 魯棒性項目調度中緩沖設置方法[J]. 控制與決策，2014，29（2）：368—372.

CUI N F，ZHAO Y，HU X J. Buffer management in robust project scheduling[J]. Control and Decision，2014，29（2）：368—372. （In Chinese）

[11]? 賈峰，江平宇，劉道玉，等. 葉片批量加工過程的誤差傳遞控制方法[J]. 計算機集成制造系統，2012，18（1）：76—86.

JIA F，JIANG P Y，LIU D Y，et al. Error propagation control method for multistage batches machining processed of blades[J]. Computer Integrated Manufacturing Systems，2012，18（1）：76—86. （In Chinese）

[12]? 王秋明，劉科成，高慧穎. 基于灰色理論與BP神經網絡的工序質量預測研究[J]. 北京理工大學學報，2011，31（2）：249—252.

WANG Q M，LIU K C，GAO H Y. Research of procedure quality forecast based on the grey theory and BP neural networks[J]. Transactions of Beijing Institute of Technology，2011，31（2）：249—252. （In Chinese）

[13]? 鞠萍華，柯磊，冉琰，等. 基于GRA和AHP的GRNN神經網絡零件失效概率預測方法[J].湖南大學學報（自然科學版），2019，46（4）：34—40.

JU P H ，KE L，RAN Y，et al.? Failure probability prediction method on parts of generalized regression neural network based on GRA and AHP[J]. Journal of Hunan University（Natural Sciences），2019，46（4）：34—40. （In Chinese）

[14]? LEE D，FUKASAWA R，RICARDEZ-SANDOVAL L. Bi-objective short-term scheduling in a rolling horizon framework：a priori approaches with alternative operational objectives[J]. Computers & Operations Research，2019，111（1）：141—154.

[15]? 張潔，秦威，宋代立. 考慮工時不確定的混合流水車間滾動調度方法[J]. 機械工程學報，2015，51（11）：99—108.

ZHANG J，QIN W，SONG D L. Rescheduling algorithm based on rolling horizon procedure for a dynamic hybrid flow shop with uncertain processing time[J]. Journal of Mechanical Engineering，2015，51（11）：99—108. （In Chinese）

[16]? DI PASQUALE V，MIRANDA S，NEUMANN W P，et al. Human reliability in manual assembly systems：A systematic literature review [J]. IFAC PapersOnLine，2018，51（11）：675—680.

[17]? 韓笑樂，鞠留紅，錢麗娜，等. 集裝箱進出口碼頭泊位-堆場協同分配的動態決策[J]. 上海交通大學學報，2019，53（1）：69—76.

HAN X L，JU L H，QIAN L N，et al. Dynamic decision making for the integrated allocation of berth and yard resources at import/export container terminals[J]. Journal of Shanghai Jiaotong University，2019，53（1）：69—76. （In Chinese）

[18]? 唐文斌. 飛機非線性裝配偏差分析與容差協同分配方法研究[D]. 西安：西北工業大學機電學院，2015：1—135.

TANG W B. Non-linear assembly deviation analysis and tolerance co-allocation for aircraft[D]. Xian：School of Mechanical Engineering，Northwestern Polytechnical University，2015：1—135. （In Chinese）

[19]? RUI J，ZHANG H，ZHANG D，et al. Total organic carbon content prediction based on support-vector-regression machine with particle swarm optimization [J]. Journal of Petroleum Science and Engineering，2019，180（1）：699—706.

[20]? 陸志強，楊超. 基于項目網絡拆分決策的多項目協同調度問題建模[J]. 上海交通大學學報，2017，51（2）：193—201.

LU Z Q，YANG C. Modeling of resource constrained multi-project scheduling problem based on project splitting[J]. Journal of Shanghai Jiaotong University，2017，51（2）：193—201. （In Chinese）

[21]? 隋惠惠. 基于BP神經網絡的短期電力負荷預測的研究[D]. 黑龍江：哈爾濱工業大學電氣工程與自動化學院，2015：1—57.

SUI H H. Research on short-term electric load forecasting based on BP neural network[D]. Heilongjiang：School of Electrical Engineering and Automation，Harbin Institute of Technology，2015：1—57. （In Chinese）