基于PSCAD的110 kV輸電線路故障測距研究

許嘯天，田 斐

（南陽理工學院 智能制造學院，河南 南陽 473004）

0 引 言

在電子化、科技化高度發達的新時代，電能成為生活中不可或缺的一部分。與此同時，傳統的電力維修和線路監測已經不能滿足當下各地區用戶的用電需求，也不符合當今中國發展新形勢下的發展要求。所以，為了保證電網持續高效運行且緊跟時代發展步伐[1]，本文利用PSCAD軟件建立了110 kV輸電線路故障測距模型。仿真結果表明：雙端測距法在對線路故障進行定位時更加快速、精確。

1 基于PSCAD的110 kV輸電線路故障測距設計

1.1 總體設計

電源電壓為110 kV，輸電線路全長300 km，本次仿真的故障點在距左側輸電線路的100 km處，設置發生的故障為單相接地短路（a相），b相和c相正常。整個仿真運行時間為0.5 s，故障發生時間為0.15 s，故障持續時間為0.05 s，之后系統恢復正常運行。仿真運行的步長設置為1 μs，行波信號的采樣頻率設置為1 MHz。PSCAD故障仿真主模型如圖1所示。

圖1中，最上方為主體電路，輸電線路TLine選用Bergeron模型。本文所采用的信號傳遞方式為無線傳遞，通過使用Radio Links元件實現數據信號的傳遞功能，將其與右下角子系統內部的信號接收連接在一起實現主電路與子系統間信號的無線傳遞。

右下方為電壓、電流封裝的子模塊系統，主要作用為：第一，對線路產生的信號進行解耦處理，即通過在其內部搭建的凱倫貝爾變換公式來進行相模變換；第二，使得主體電路有條有理。子系統內部搭建圖如圖2所示。

在圖2中，子系統內部最上方對接收到的信號進行分解，即分解成所需要的a、b、c三相電氣量。這里為了敘述簡便，只列出其中一張內部封裝搭建結構圖，即左電流子系統，其他類似。

1.2 單端測距

單端測距是指僅利用一側電壓電流的波形進行定位，即通過初始反射波在故障點F與P端多次反射過程來實現定位[2]。線路全長為L，P端為線路左端，Q端為右端，各自都裝上電壓、電流互感器。故障F點發生在距離P端x處。其中，由于波的反射效果，測量出兩次反射時間t1、t2，但由于經過幾次反射之后波形的變化更加微小，不方便分析，所以只選取最開始測量的兩次反射時間作故障測距分析。計算故障距離公式如（1）所示。

1.3 雙端測距

雙端測距以故障所形成的初始行波抵達線路兩端的時間差來得到故障點的具體位置[3]，原理模型如圖3所示。

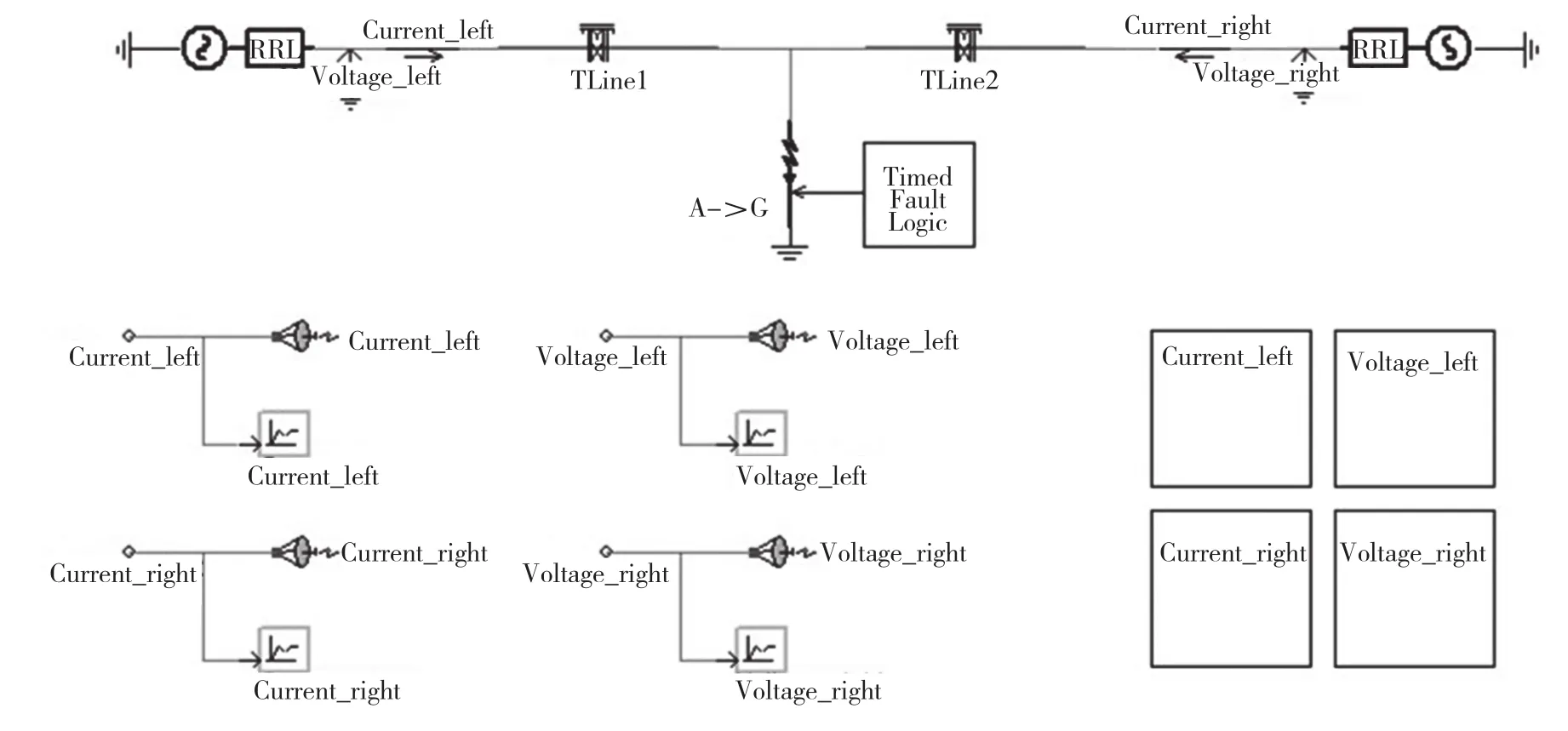
圖1 PSCAD故障仿真圖

圖2 子系統內部搭建圖

圖3 雙端測距原理圖

其中反射波和折射波分別經過時間t1、t2到達線路P、Q端，波速為v，則故障距離x的計算按照式（2）和式（3）進行。

將式（2）、式（3）綜合，得到最終故障距離x，如式（4）所示。

1.4 相模變換

輸電線路三相電氣量之間具有耦合關系，這將對故障測距仿真結果的準確性產生干擾[4]。所以，為了消除三相導線之間相互耦合問題的影響，運用凱倫貝爾變換矩陣具有相互獨立的方程式這一特點，對其進行解耦，即相模變換。

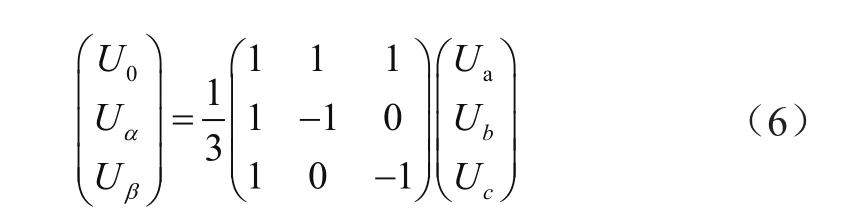
式中，三種變量I0、Iα、Iβ分別由相電流I0、Ib、Ic通過獨立方程得到的0模、α模和β模分量；U0、Uα、Uβ分別由相電壓U0、Ub、Uc通過獨立方程得到的0模、α模和β模分量。

實際經驗表明，0模分量易受到線路電容和電感的影響，并且隨著頻率的升高衰減嚴重，會造成其波速的不穩定。但是，線模分量大體上在導體中運動，波速相對比較穩定。所以，將選取線模行波信號作為小波分析的依據。由于行波波速并不是固定不變的，在不同的輸電線路中，其值也會出現一定的變化，本文以線路TLine的Bergeron模型參數得出波速大小。

1.5 小波分析

小波變換對目標信號實行局部化分析，具有優異的故障檢測靈敏性。在小波變換中，將運用到其中一個功能，即采樣。本文選用離散小波變換元件（Discrete Wavelet Transform）中的高頻分量[5]，高頻分量在信號發生突變時刻會顯示出尖峰，而平緩變化時其值近似為零。運用高頻信號來分析信號的突變點，并在波形圖中描出故障信號突變的時間點，進而為計算故障距離提供數據依據。

2 結果分析

經過相模變換后的故障信號需要進一步進行小波變換處理，并放大其信號突變位置，以便于能清晰地標出電流、電壓信號突變點，即電流、電壓模極大值，從而得出最終所需要的結論。此處選用左右電壓的α模，高頻信號分量D。小波變換圖如圖4所示。

圖4 小波變換圖

其中，分別將左端電壓波形圖中第一、二次發生信號突變，即模極大值記錄下來，分別為150.347 ms、151.041 ms，并將其帶入式（1），得出單端故障測距的結果為101.5056 km。

同時，將對應的右端電壓波形圖中第一次發生信號突變即模極大值記錄下來，為150.6905 ms，并將其帶入式（4），得出雙端故障測距的結果為99.7 km。

與左側100 km處故障設置點對比，可得采用單端測量誤差為1.505 6 km，而采用雙端測量誤差僅為0.3 km。所以，在實際生活中更加傾向于采用雙端故障測距法來檢測線路，以滿足實際需要。