基于貝葉斯信息更新的無人機目標搜索策略研究

李 悅，周長銀

(山東科技大學 數學與系統科學學院,山東 青島 266590)

軍事和災害救助中，目標搜索是目前無人機應用中的一個重要方面。相對于人工搜索，無人機搜索目標受困于對目標信息的掌握程度和無人機搜索策略，需要更好的決策算法。

針對目標搜索問題的研究，Koopman[1]早在第二次世界大戰期間就提出了基本的目標搜索理論，基于目標靜止、均勻分布以及在搜索區域內勻速連續搜尋的假設，提出了發現概率模型。在Koopman的假設下，Frost[2]通過設計“掃地”實驗對發現概率和掃海寬度等作了詳盡闡釋；Koester等[3]提出基于搜尋區域大小、掃海寬度和搜索努力程度的發現概率計算方法。為了突破均勻分布假設的限制，Brown[4]考慮了在離散空間中對移動目標進行搜索的最佳策略問題。周濤[5]對海上搜尋中發現概率的預測值進行研究,但沒有提出針對掃海寬度等因素的更好策略。在海上搜索中，影響發現概率的核心因素是掃海寬度。吳翔等[6]就這一因素進行重點探討，并提出了掃海寬度的修正模型和指數探測函數的修正模型。王博研[7]將影響發現概率的因素結合起來考慮，提出了計算初始搜尋區域中搜尋成功率的方法。上述文獻提出的模型和方法，在研究無人機目標搜索問題時值得借鑒和參考，但所給搜索過程都是確定性的，不能利用搜索過程獲取的新信息實時地更改搜索策略。

2011年，Stone等[8]利用貝葉斯方法提出搜尋失事飛機的數學模型，找到了墜落近兩年的法航447。2015年，Lu等[9]利用貝葉斯推理給出了最優搜救模型。Lu[10]著重研究了墜毀飛機的定位方法，確定救援區域和搜索策略。

在關于無人機目標搜索的研究中，多無人機協同搜索問題得到研究人員的更多關注[11-12]。協同搜索假設目標所在區域服從均勻分布。該假設在目標位于搜索區域的分布信息未知的情況下是合理的，但若目標所處位置有明顯的分布特征，則需要其他假設。

本研究借助貝葉斯信息更新方法，研究利用無人機進行目標搜索策略問題，提出目標搜索的動態策略和相應算法，并在正態分布假設下進行數值模擬，驗證所給方法的適用性。

1 基于貝葉斯更新的發現概率模型

發現概率是指目標100%位于某一個區域時，無人機發現該目標的概率。發現概率的大小與無人機搜索區域面積有關，也與無人機搜索設備掃視面積有關。假設無人機采取平行搜索，執行搜索任務時的掃視寬度為ω，搜索設備單位時間的掃視距離不變，并假設每個搜索階段的搜索面積相同。

為便于計算發現概率和確定最優搜索區域，采用離散化方法，把目標所在區域Ω分割為N個邊長為ω的正方形區域R1,R2,…，RN。假設目標位置的初始信息集合記為D0，根據D0可以給出目標位于Rk的先驗概率為P(BRk|D0)[13]，k=1,2,…,N,其中BRk表示目標位于區域Rk這一事件。

記R(t)是第t階段的任務搜索區域，假設R(t)是由R1,R2,…，RN中m×n個相連的小正方形R1(t),R2(t),…，Rm×n(t)組成，此時，無人機實際搜索區域面積為mnω2，且

R(t)={R1(t),R2(t),…，Rm×n(t)}?{R1,R2,…,RN}。

AR(t)表示無人機在區域R(t)內搜索時發現目標這一事件，則目標被發現的概率為

(1)

其中P(ARi(t)|BRi(t),Dt-1)表示目標位于Ri(t)時發現目標的概率[14]，表示為

(2)

其中zi(t)表示在R(t)內每一小區域Ri(t)上的掃視距離。則由(1)式，有

(3)

當搜索進行到t階段時，可以通過多種方法確定最優搜索區域[15-16]。本研究以發現概率確定最優搜索區域，發現概率根據式(1)算出。原則上，選取發現概率P(AR(t)|Dt-1)最大的區域R(t)作為搜索區域。

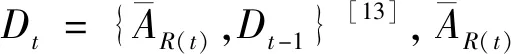
(4)

t+1階段的目標搜索區域R(t+1)由m×n個相連的小正方形R1(t+1),R2(t+1),…,Rm×n(t+1)組成，可表示為：

R(t+1)={R1(t+1),R2(t+1),…,Rm×n(t+1)}?{R1,R2,…,RN}，

則t+1階段目標位于區域Ri(t+1)(i=1,2,…,m×n)上的先驗概率P(BRi(t+1)|Dt)可由(4)式給出，進而由(3)式，可計算t+1階段目標被發現的概率P(AR(t+1)|Dt)。

以上搜索區域的確定過程可以重復進行下去，直到目標被發現為止。若經過s個階段才發現搜索目標，則“前s個階段搜尋發現目標”的累計發現概率定義為：

(5)

2 最優搜索策略

單位時間搜索設備內掃視距離v0稱為掃視速度。假設無人機在一次搜索任務中的最大停留時間為T。最優搜索策略是在給定條件下發現概率最大的策略，記為Z(t)={Z1(t),Z2(t),…,Zmn(t)}。

最優搜索策略可由如下規劃給出：

(6)

這里要求v0T≥mnω，即無人機的掃視面積v0Tω不小于實際搜索面積mnω2，在實際應用中是合理的。

結合以上分析，給出基于貝葉斯更新的最優搜索算法如下：

Step 1:給出初始先驗分布P(BRk|D0)；初始值v0,T,n,m；t=1；

Step 2:根據(6)式求解t階段的最優搜索策略(Z*(t),R*(t))；

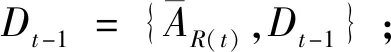
Step 4:利用(4)式，更新先驗分布P(BRi(t+1)|Dt)，計算發現概率P(AR(t+1)|Dt)；

Step 5:令t=t+1，返回Step 2。

需要注意，如果在下一階段搜索前，有額外信息獲得，例如獲得目標位置的新線索，這時需要對信息集Dt-1的更新進行干預，加入額外信息。同時，搜索區域目標位置的先驗分布也可能發生變化，相應地，須對先驗分布P(BRi(t)|Dt-1)重新調整，具體調整方法在下節數值實驗中給出。

3 數值模擬

在目標搜索的研究中，通常把目標最有可能的位置坐標稱為基點，基點可能不止一個。設M是基點個數，fk(x,y)是目標位于第k個基點所在區域內的概率分布，假設fk(x,y)為二維正態分布。

3.1 無貝葉斯干預下的模擬實驗

目標位于區域Rk內的初始概率計算公式：

(7)

假設在Ω內有5個基點A、B、C、D、E，以這5個基點將Ω劃分為5個區域，每個區域又劃分為3×3個等面積的小區域。5個區域的概率分布以及概率信息如表1所示。

表1 概率分布與概率Tab.1 Probability distribution and probability

根據(7)式計算每個區域在該區域概率分布下的概率，然后挑選出概率最大的三個區域作為任務區域。接著將任務區域的概率進行歸一化，公式如下：

(8)

其中n為選擇出的任務區域ΩR的個數。

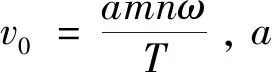
為了避免實驗的偶然性，取a∈[1,2]，間隔為0.2進行實驗。對最優搜索策略模型進行求解可得每個階段的發現概率如表2(表中用P1代替P(BR1|D0)，P2代替P(BR2|D0)，P3代替P(BR3|D0))。

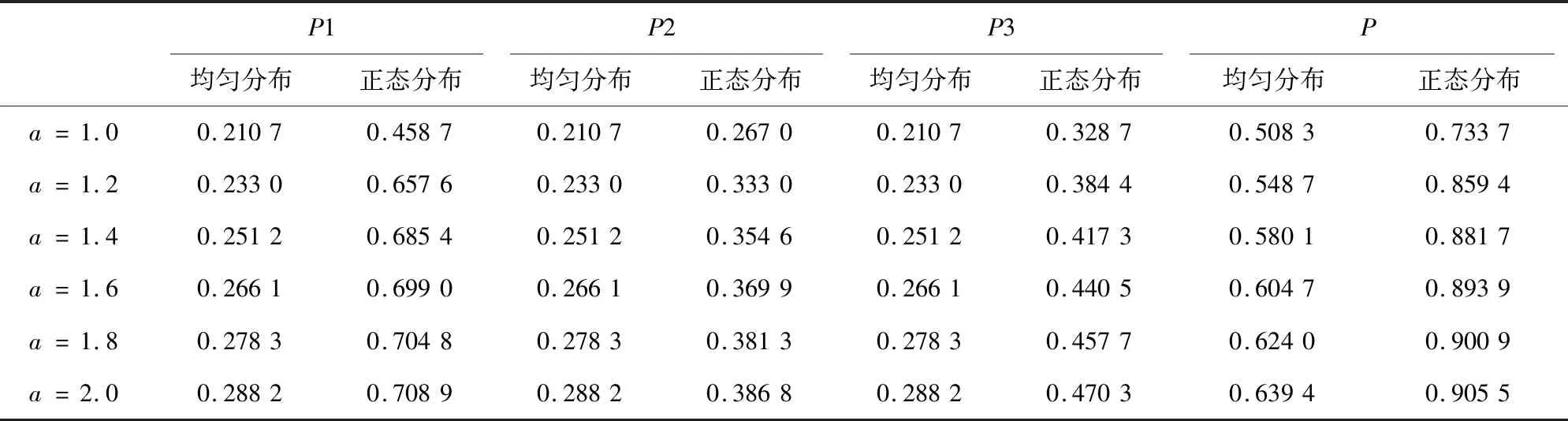
表2 無貝葉斯干預的發現概率Tab.2 Probability of discovery without Bayesian intervention

從表2中可以看到，選取正態分布比均勻分布得到的累積發現概率更大。這是由于均勻分布在目標所處搜索區域的概率分布是相同的，但是正態分布在目標所處搜索區域的概率分布在正態分布的峰值處最大，因此累計概率更大。在正態分布與均勻分布下，每階段發現概率的變化分別如圖1和圖2所示。

從圖1和圖2中可以看出，不論是正態分布還是均勻分布，每個階段的發現概率都隨著a的增大而逐漸增大。說明掃視面積系數a對發現概率有一定影響，但是根據圖1和圖2中直線之間的距離來看，發現概率的增大與a的增大不是線性關系。

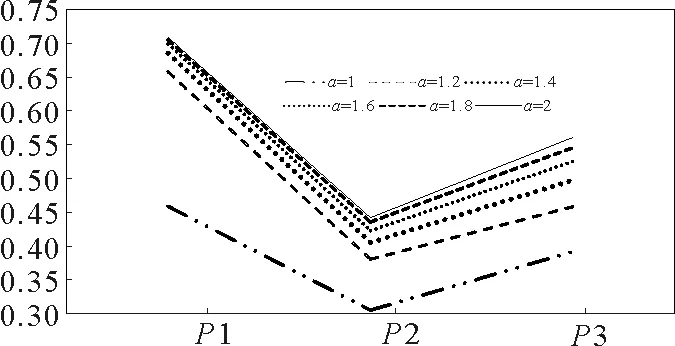
圖1 正態分布下每階段發現概率Fig.1 Probability of discovery at each stage under normal distribution

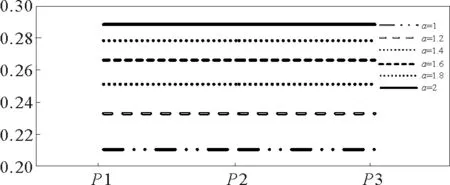
圖2 均勻分布下每階段發現概率Fig.2 Probability of discovery at each stage under uniform distribution

3.2 有貝葉斯干預下的模擬實驗

在3.1節實驗中加入貝葉斯干預，即在完成第一階段搜索之后，加入一個新的信息NF(-6,13;8,8;0)，pF=0.52>pA，則更新F區域為第二階段搜索區域，A區域為第三階段搜索區域，此時每個階段的發現概率如表3。

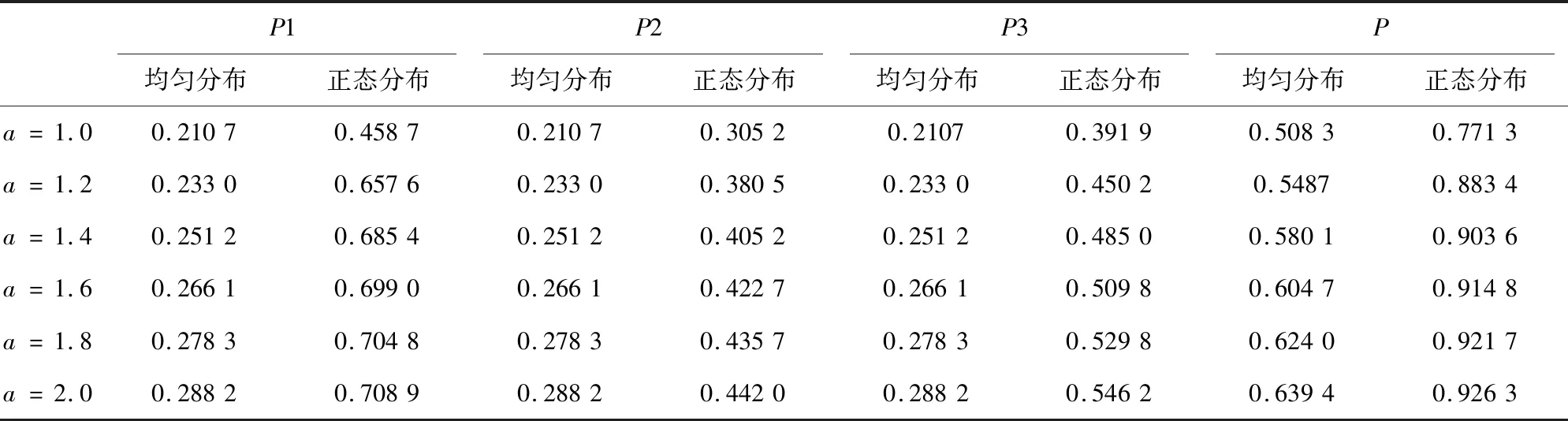
表3 貝葉斯干預下發現概率Tab.3 Probability of discovery under Bayesian intervention

從表2和表3中可以看出，加入貝葉斯干預后，第一階段的發現概率是相同的，說明貝葉斯干預對干預前一階段的發現概率沒有影響；而第二階段與第三階段的發現概率均有增加，這是由于加入貝葉斯干預后，概率分布重新調整，干預后新加入的區域比原區域目標存在的概率大，因此發現概率也增大，累計發現概率也會增大。圖3給出了有貝葉斯干預和無貝葉斯干預情況下的累計發現概率對比。

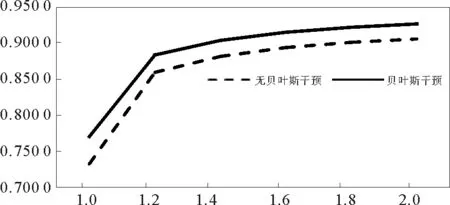
圖3 有無貝葉斯干預下累計概率對比Fig.3 Comparisons of cumulative probability with and without Bayesian intervention

從圖3中能夠明顯看出在加入貝葉斯干預后累計發現概率增大，尤其是a=1到a=1.2時，增長趨勢明顯。這是由于加入貝葉斯干預后，概率進行重新分配，第二階段與第三階段所占概率比相較之前較高，因此發現概率增大，累計發現概率也會增大。

4 結論

在已有文獻中，大都假設目標位于搜索區域位置的分布為均勻分布，但通常情況下，由于預先獲取了目標所在區域的分布以及該區域的地理特點信息，容易推斷目標在某一些基點上的分布概率可能大一些，在其他位置則可能小一些。因此，在已掌握這些信息的情況下，均勻分布的假設就顯得不盡合理。本研究首先確定目標的初始先驗分布，然后計算每個目標在相同區域內的初始概率，選擇合理的任務區域后，將任務區域概率歸一化，最終得到目標在搜索區域上的概率分布，最后給出最優搜索策略。基于貝葉斯更新思想，利用貝葉斯公式獲取目標信息的后驗分布，進而由所給目標搜索策略模型做出決策，保證了搜索信息在不同階段的動態傳遞性。同時，由于使用貝葉斯干預，在貝葉斯更新過程中能夠采用目標新信息，使得所做決策更具實時性和合理性。

所給模型也有一定局限性。首先，在對海上搜索目標制定搜索策略時，由于目標隨洋流漂流移動，會帶來較大誤差。解決這個問題，可以通過對正態分布密度函數進行改進，加大基點在洋流方向上概率分布的拖尾來實現。其次，沒有考慮多無人機協作的搜索策略問題，搜索成本、無人機最大工作時間等因素也是需要進一步考慮的問題。