不同噴射條件下閃蒸噴霧液滴尺寸特性數值分析

柯炳正， 高璞珍， 王博， 李茹， 盧川， 田瑞峰

(1.哈爾濱工程大學 核安全與仿真技術國防重點學科實驗在室，黑龍江 哈爾濱 150001；2.中國核動力研究設計院 核反應堆系統設計技術重點實驗室，四川 成都 610213)

閃蒸噴霧行為存在于很多工業領域中，如當核電站發生一回路冷卻劑喪失事故(loss of coolant accident, LOCA)時，大量高溫高壓冷卻劑從承壓管路的破口處以閃蒸噴霧的形式快速向外界噴出，造成安全殼內壓力溫度急劇升高，安全殼的完整性受到嚴重威脅[1]。閃蒸噴霧屬于非平衡熱力學過程，其相變情況十分復雜，很多學者對閃蒸噴霧現象進行了數值模擬研究。Marsh等[2]使用6方程模型模擬噴嘴閃蒸流動，考慮了由成核和相變引起的相間質量、動量以及能量的傳遞。Janet等[3]通過使用CFX 14.5中的5方程模型研究了閃蒸噴嘴流中各種成核模型的性能。Mimouni等[4]使用NEPTUNE CFD中的6方程模型模擬了閃蒸空化流動，通過使用確定的傳熱系數確保蒸汽溫度接近飽和溫度。季璨[5]利用離散相的DPM模型和用戶自定義函數對閃蒸罐內的外部閃蒸噴霧現象進行研究。聶永廣等[6]結合混合物模型與用戶自定義函數，計算出瀝青噴霧造粒噴嘴中的戊烷閃蒸情況。在閃蒸噴霧的研究領域中，文獻[6-11]對燃料在內燃機中的閃蒸噴霧以及對真空中制冷劑閃蒸關注較多，而在液態水閃蒸噴霧的研究領域中，雖然有學者進行了一定的研究[5]，但對于閃蒸噴霧液滴的外部尺寸特性研究偏少。本文利用計算流體力學軟件FLUENT對不同噴射條件下閃蒸噴霧過程進行計算模擬研究，對閃蒸噴霧過程中液滴尺寸的變化特性進行分析，得到不同初始壓力，噴口直徑和噴射距離時，閃蒸噴霧液滴尺寸的變化規律。

1 閃蒸噴霧數值方法及驗證

1.1 閃蒸噴霧數值方法介紹

在本文建立了一個150×150×1 200的計算區域并劃分結構化網格，如圖1所示。為了使計算更準確，對計算區域進行了網格無關性驗證。在計算區域內計算了不同網格數量下，流動空氣在200 mm處的截面平均流速，空氣的入口流速設為1 m/s。其計算結果如圖2所示。

圖1 計算區域網格圖Fig.1 Grid of calculation domain

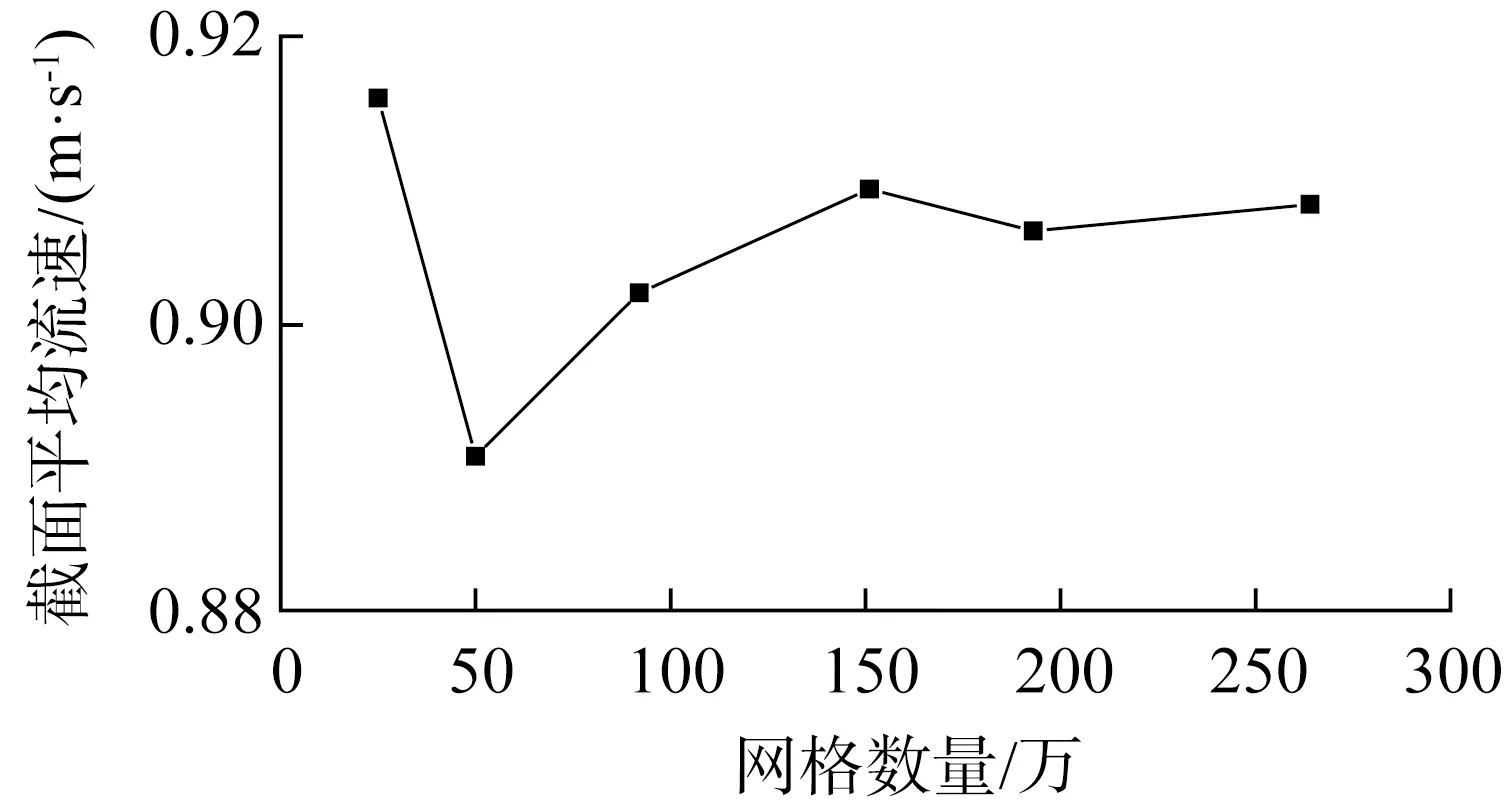
圖2 網格無關性驗證結果Fig.2 Grid independence verification results

從驗證結果中可以看出，當網格數量達到150萬以上時，網格數量對計算結果的影響很小。本研究中計算區域的整體網格數量為165萬。

研究利用離散相模型中的過熱噴射器模型模擬閃蒸噴射，連續相入口和出口條件均為壓力邊界，離散相邊界條件為逃逸邊界條件。初始噴射環境溫度設置為23 ℃，初始環境壓力為大氣壓，初始水蒸氣濕度設置為0.5%。離散相考慮了液滴顆粒受到加熱冷卻及相變的影響，同時考慮了壓力變化導致的飽和溫度變化的影響，液滴曳力的模型為動力阻力模型，液滴二次破碎模型采用了開爾文亥姆霍茲-瑞利泰勒破碎(Kelvin-Helmholtz and Rayleigh-Taylor hybrid wave, KHRT)模型[12]。液滴溫度設為初始計算壓力下的飽和溫度，液滴尺寸分布為Rosin-Rammler分布。壓力速度耦合算法、梯度插值分別采用壓力耦合半隱式算法以及基于節點的格林高斯插值方法，其他插值采用二階迎風格式。

1.2 液滴特性研究

本研究中的液滴尺寸特性以在計算域不同截面處計算得到的索特平均直徑(Sauter mean diameter, SMD)進行分析。索特平均直徑d32是一種描述噴霧液滴尺寸的參數，在流體力學領域中，該參數被廣泛應用于顆粒粒徑分布的研究中[13]。其定義是與所研究的顆粒群的總體積與總表面積之比相同的一群同等大小的顆粒群中，單個顆粒的直徑大小。 索特平均直徑d32為：

(1)

式中：dv和ds分別代表體積定義的直徑與表面積定義的顆粒直徑；Vp為液滴總體積；Ap為液滴總表面積。

在閃蒸噴射的研究中，選擇合適的噴霧液滴破裂模型是成功模擬噴霧過程，得到合理的液滴尺寸分布結果的關鍵。本文閃蒸噴霧過程屬于高速條件下的射流噴霧過程，在高速條件下，射流液滴的破裂是空氣動力、表面張力和液滴黏滯力相互作用的結果。這些力的相互作用可以以韋伯數We和奧內佐格數Oh來表示。

韋伯數We以及奧內佐格數Oh的分別為：

(2)

(3)

式中：ρ為液滴密度；u為特征流速；d為特征長度；σ為表面張力；μ為動力粘度。

從式(2)、(3)中可以看出，韋伯數We表示的是空氣動力與表面張力的關系，奧內佐格數Oh則表示液滴黏滯力和表面張力的關系。在閃蒸噴射中，由于射流流體速度快，射流的韋伯數We很大，射流破裂形式主要為霧化形式[14]。

目前在射流噴霧霧化模型的研究中，比較常用的有泰勒類比破碎(Taylor analogy breakup, TAB)模型[15]和KHRT模型[12]。

1.2.1 泰勒類比破碎模型

TAB模型將液滴的行為與振蕩彈簧質量系統相結合，將液體受到的表面張力、液體阻力、液體黏性力分別與振蕩彈簧質量系統中彈簧回復力、外力以及彈簧阻尼力進行類比。液滴在氣動力的作用下產生形變，當形變達到臨界時，液滴發生破裂產生子液滴。液滴形變為：

(4)

式中：y表示液滴發生形變的無量綱量；ρl和ρg是離散相和連續相密度；u是液滴的相對速度，r是未產生形變的液滴半徑；σ是液滴表面張力；μl是液滴粘度；CF、CK和Cd為無量綱常數。

當y≤1時，液滴不斷振蕩變形；當y>1時，液滴發生破裂，產生子液滴。子液滴的速度為：

(5)

式中CV為常數。

1.2.2 開爾文亥姆霍茲-瑞利泰勒破碎模型

KHRT模型將開爾文-亥姆霍茲(Kelvin-Helmholtz)不穩定波理論與瑞利泰勒(Rayleigh-Taylor)不穩定波理論相結合，共同預測射流中液滴的破碎情況。該模型將射流破碎分為一次破碎和二次破碎這2個過程，一次破碎過程中，將射流整體當作是直徑與噴口直徑相當的大液滴，利用KH不穩定波理論對該液滴的破裂進行模擬計算。

破裂產生的子液滴半徑為：

rc=B0ΛKH

(6)

式中ΛKH是對應于具有最大生長速率的KH波的波長；B0是等于0.61的常數。

在二次破碎過程中，模型將RT模型與KH模型結合使用來預測液滴的破碎。

RT模型中增長最快的波的頻率與波數為：

(7)

(8)

式中：gt是行進方向上的加速度；ρl和ρg分別為液相和氣相的密度。

由RT模型計算得到的新的子液滴的半徑為：

(9)

式中CRT為常數，CRT=1。

在KHRT模型中引入了液體核心破碎長度的概念，當液滴破裂發生在液體核心破碎長度內，破裂只考慮KH模型的影響。當破裂發生在液體核心破碎長度外，液滴的破裂則考慮KH模型RT模型的共同作用。

TAB模型雖然在噴霧雷諾數較低時計算結果較為理想，而當雷諾數較大時，計算結果偏差較大。而KHRT模型在雷諾數較大的噴霧情況中計算結果較為理想[16]。在本次研究中，由于液體的溫度和壓力高于大氣壓，當液體噴放至大氣環境中時，液體與環境的相對流動速度大，雷諾數很大。因此TAB模型并不適用，最終本研究的液滴破碎模型選擇的是KHRT模型。

1.3 數值計算方法驗證

為了驗證本研究中采用的數值計算方法是否合理，利用文獻[17]中測量得到的液滴索特平均直徑的實驗數據和數值計算的結果進行了對比分析。

圖3展示了噴嘴直徑d為0.75 mm和1mm時，液滴的索特平均直徑隨噴霧距離變化的實驗數據與計算結果對比情況。

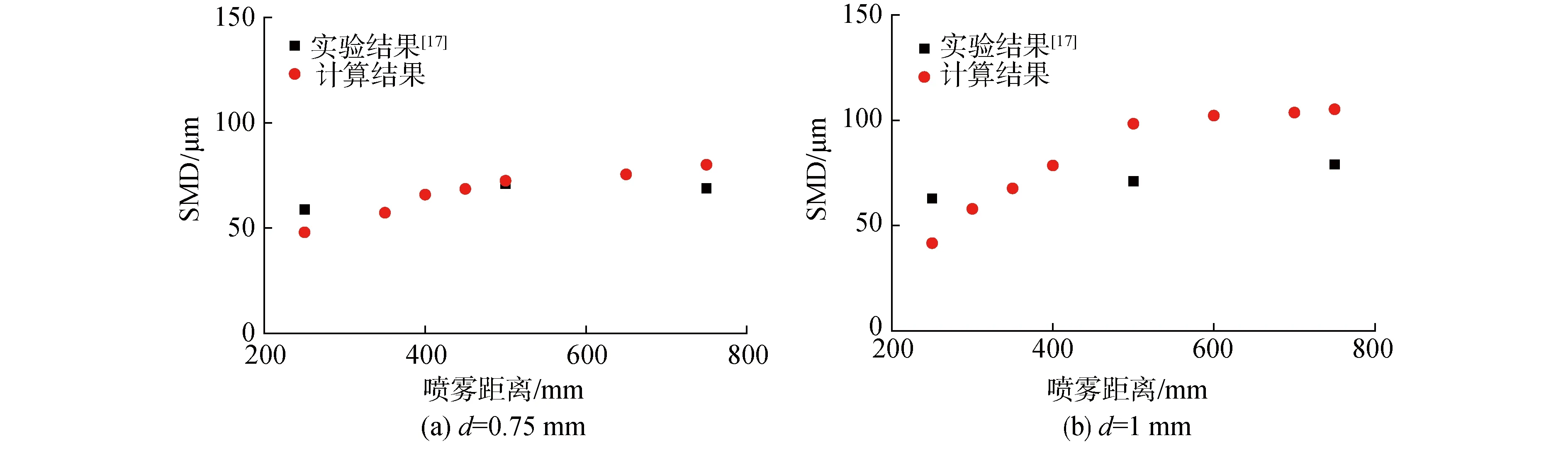
圖3 實驗與計算結果對比Fig.3 Comparison of experiment and calculation results

通過對實驗與計算結果的分析可知，在250 mm到750 mm的噴霧距離的范圍內，在2種工況下計算結果與實驗數據在數值上存在一定偏差，在d為0.75 mm的條件時計算結果與實驗結果的最大偏差為13.98%；d為1 mm時計算結果與實驗數據的最大偏差為24.90%。

雖然計算結果與實驗數據依然有一定數值上的差距，但是2者之間偏差在合理區間之內，因此在本次研究中利用該數值計算方法是合理的。

2 數值計算結果與分析

本文研究了噴霧初始壓強范圍在0.2～2.0 MPa的計算工況下，液滴索特平均直徑變化規律；噴霧噴口直徑范圍在2～4 mm的計算工況下，液滴索特平均直徑的變化規律；噴霧距離范圍200～1 000 mm的計算工況下，液滴索特平均直徑的變化規律。

2.1 不同噴霧初始壓力的影響

圖4為噴霧噴口直徑為1 mm，噴霧初始壓強在0.2～2.0 MPa，噴霧溫度為120 ℃～212 ℃，環境壓強為0.1 MPa時，噴霧距離分別為200、400、600、800和1 000 mm時，液滴SMD的變化規律。

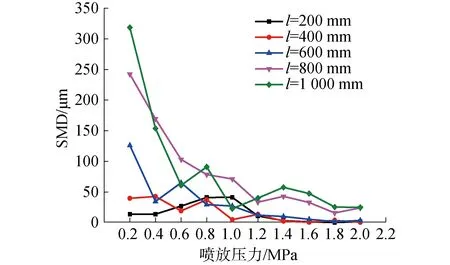
圖4 不同初始壓力的SMD結果Fig.4 SMD results of different initial pressures

隨著初始噴霧壓力的提高，噴霧液滴的索特平均直徑不斷降低。當噴霧距離為600、800和1 000 mm時，在初始噴霧壓力1.0 MPa之前，噴霧液滴的SMD下降較快，當初始噴霧壓強在1.0～2.0 MPa時，索特平均直徑的變化趨勢趨于平緩。而當噴霧距離為200～400 mm時，索特平均直徑在0.2～2.0 MPa的壓強區間內一直呈現平緩的下降趨勢。在過熱噴放過程中，噴放流體與環境中的氣體存在較大的速度差，環境氣體對噴放流體存在氣動力的作用。在該氣動力的作用下，噴放流體產生流動不穩定性，破裂的不同尺寸的子液滴。同時由于液相流體的溫度高于在環境下的飽和溫度，噴放流體以及子液滴中產生了大量的汽化核心，部分液體發生閃蒸相變，成為蒸汽。隨著閃蒸相變的不斷發生，液相流體尺寸逐漸減小。而在閃蒸相變和外部氣動力的共同影響下，噴放流體以及子液滴繼續發生破碎，產生了更加細小的液滴。

當噴霧初始壓力提高時，噴口處兩相流體質量流量升高，汽化核心數量提高，使得更多的液滴發生閃蒸相變。同時大量閃蒸相變產生的蒸汽和液滴混合，使得射流更加劇烈，液滴的韋伯數增大，氣動力對液滴破裂的影響增大，射流中的液滴發生破裂的幾率更大，液滴的平均粒徑隨著噴霧初始壓力的提高不斷減小。當壓力持續增大時，在噴口附近兩相流以臨界流的形式流出，由于在臨界流中，流體以臨界流速流動，所以當壓力繼續增大時，流體的流量不變，外部氣動力對射流的影響不變，因此只有液滴的自身參數對破裂產生影響，液滴的平均粒徑減小的趨勢趨于平穩。

2.2 不同噴霧噴口直徑的影響

圖5展示了噴霧壓強1 MPa，噴霧溫度為179 ℃，噴霧噴口直徑在2.0～4.0 mm，環境壓強為0.1 MPa的范圍時，噴霧距離分別為400、500、600、700、800和900 mm時，液滴索特平均直徑的變化規律。

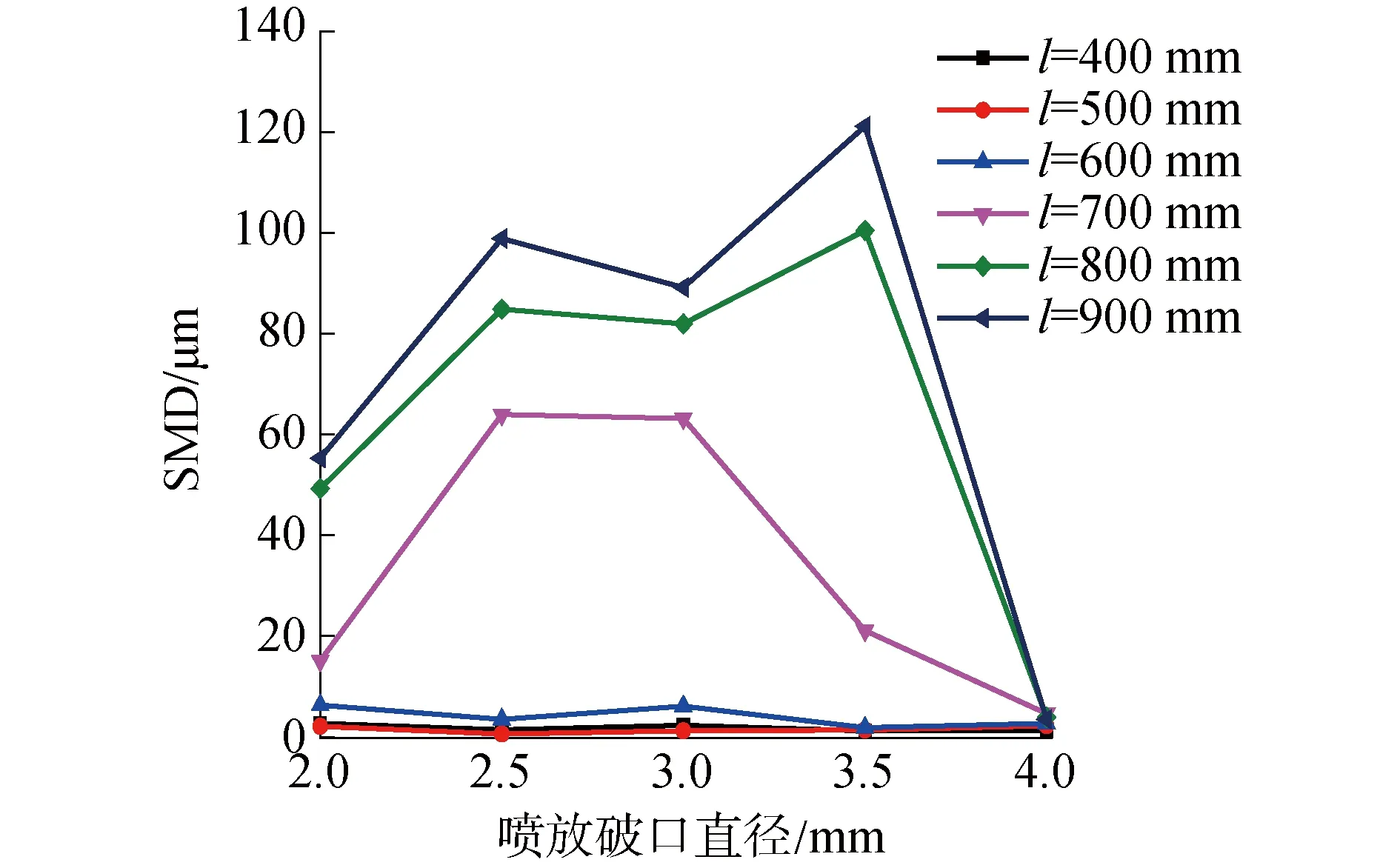
圖5 不同噴口直徑的SMD結果Fig.5 SMD results of different injector diameters

當噴口直徑增大時，噴霧液滴的索特平均直徑呈現一種先增大后降低的趨勢。而且當噴霧距離越大時，變化趨勢越明顯，噴霧液滴索特平均直徑越大。當噴霧距離為400 mm和500 mm時，液滴索特平均直徑基本無變化。由于噴霧壓強為1 MPa，在噴口處的流動屬于兩相臨界流。噴口直徑的增大導致噴射面積增大，射流流體的整體流量增大。整體流量的增大導致流體的相對體積增大，射流內部與環境的換熱發生惡化，射流中汽化核心密度相對減少，閃蒸汽化的影響減弱，使得SMD有增大的趨勢。但是由于射流處于臨界流動狀態，流體仍以臨界流速流動，隨著噴口直徑的增大，流體的韋伯數增大，氣動力對液滴破裂的影響提高，由氣動力作用產生的液滴破裂增多，從而導致液滴的SMD變小。在噴射直徑增大的初期過程中，射流流體的流量增大，此時閃蒸汽化對液滴尺寸變化的影響起到了主要作用，使得液滴SMD相對增大。而當噴射直徑持續增大時，射流流體的韋伯數持續增大，此時氣動力對液滴尺寸變化的影響增大，成為主要的影響因素，導致大量液滴破裂，SMD隨之減小。

2.3 不同噴霧距離的影響

圖6(a)展示了噴霧噴口直徑為1 mm，噴霧溫度為飽和溫度，噴霧距離為200～1 000 mm，環境壓強為0.1 MPa的范圍時，噴霧初始壓強分別為0.4、0.8、1.2、1.6和2.0 MPa時，液滴SMD的變化規律。

圖6(b)展示了噴霧初始壓力為1 MPa，噴霧溫度為179 ℃，噴霧距離在200 mm至1 000 mm的范圍時，噴霧噴口直徑分別為2、2.5、3、3.5和4 mm時，液滴SMD的變化規律。

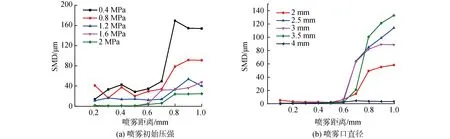
圖6 不同噴霧距離的SMD結果Fig.6 SMD results of different injector downstream distances

隨著噴霧距離的增加，噴霧液滴的SMD不斷增大，在600 mm之前，SMD變化趨勢較為平緩，而且液滴SMD較小，在60 μm以下。當噴霧距離達到600 mm時，液滴SMD的增加趨勢明顯，達到了100～200 μm。在噴霧距離為600 mm之前，噴口噴放的兩相流體大部分處于過熱狀態，當射流噴放至環境中時，在噴放流體及子液滴中發生閃蒸現象，產生大量的蒸汽，使得液滴的尺寸處于較小的范圍。同時由于射流流速較快，韋伯數較大，氣動力對液滴破裂的影響也很大，在兩者的共同作用下，流體內的液滴SMD在較小的數值區間內變化。當噴霧距離達到600～800 mm時，射流整體的壓力和溫度大幅下降，閃蒸相變對液滴尺寸變化的影響減少，同時射流流速降低，液滴的韋伯數減小，氣動力對液滴破裂的影響也減小。由于冷凝作用，在之前相變產生的部分蒸汽冷凝成液滴聚集在一起，從而導致液滴SMD不斷增大，且變化趨勢明顯。

3 結論

1)初始噴霧壓力越高，噴射流體受到的氣動力和閃蒸相變的影響越大，液滴的索特平均直徑越小；當初始噴霧壓力增大至一定程度后，氣動力對流體的影響不再變化，液滴直徑減小趨勢變緩。

2)隨著噴霧噴口直徑的增大，閃蒸汽化的影響減弱，但氣動力對液滴破裂的影響提高，噴霧液滴的索特平均直徑先增大后降低。且當噴霧距離越大時，變增大趨勢越明顯。

3)當噴霧距離增加時，閃蒸相變作用和氣動力的影響減小，噴霧液滴的索特平均直徑整體變化趨勢呈現先平穩波動后劇烈上升的情況。