光路偏振串擾誤差對閉環光纖陀螺精度影響

宋昱寰， 管練武， 高延濱， 胡文彬

(1.航空工業第一飛機設計研究院，陜西 西安 710089; 2.哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001)

由于光纖陀螺具有精度高、可靠性好等優點，相比于傳統機械轉子陀螺儀，其具有無轉動部件、結構簡單、成本低、便于批量生產等特性[1-2]。在軍事和民用范圍具有廣泛的應用價值以及應用前景。光纖陀螺的硬件部分由光路和電路2部分組成。光路部分的光纖環作為敏感光纖陀螺角速率輸出的重要元件，當環境溫度發生變化時，光纖環的性能會受到影響[3]，為降低溫度變化導致的非互易性，一般采用對稱繞法[4]。除此之外，在繞制光纖環時由于工藝原因還會在光路中引入應力雙折射點，產生非互易性誤差，導致光纖陀螺精度不能達到預期要求。文獻[5]中建立光纖陀螺光路數學模型時，默認光纖環中僅存在一個偏振串擾點，故建立模型與實際光纖環有區別，與實際得到的相位誤差不符。文獻[6]在建立光纖陀螺光路的數學模型時未考慮不同溫度情況下光路中器件的變化，與工程應用中的實際環境不符，不具有一般性。

本文充分考慮光路中的熔接點、光學器件參數，通過相干矩陣表示輸入光信號特性、瓊斯矩陣表示光學器件的傳輸特性以及熔接點。利用麥克爾遜干涉儀檢測光纖環中偏振串擾點位置和強度。完善光纖陀螺光路模型，使之適用于工程環境下。為驗證模型的準確性，本文通過理論仿真分析和實驗結果分析溫度對光纖陀螺靜態零偏的影響，證實本文提出的方法能夠作為光纖環質量評估手段。

1 光路部件及光纖陀螺光路建模

光纖陀螺誤差源有2大部分：1)由于光路中各器件尾纖相接時，存在對軸誤差角度，導致光信號傳輸至熔接點處時將發生偏振串擾現象；2)由于在繞環時工藝水平的限制以及操作不當引入的偏振串擾點。除此之外當溫度環境發生變化時，這些偏振串擾點的位置和強度也隨之變化。

對光纖陀螺光路中的光學器件進行建模[7]，系統分析偏振串擾誤差對光纖陀螺輸出精度的影響。設定光波向光纖環傳播的方向為順時針，反之為逆時針，不考慮電路系統對光路的影響。光纖陀螺光路部分包括SLD寬帶光源、光纖耦合器、光纖環、Y波導和PIN-FET探測器。根據光傳播的途徑對光學器件建模。文獻[8]可以得到與光源偏振相關的光源相干矩陣模型；文獻[9]可以得到光纖耦合器的瓊斯矩陣；文獻[10]可以得到與Y波導中起偏器的消光比ε相關的光纖偏振器瓊斯矩陣模型以及加±π/2的相位調制時相位調制器的瓊斯矩陣模型。

在目前相關的文獻中，建立光纖環瓊斯矩陣時，一般假設光纖環中僅存在一個串擾點[11]，但在實際情況中光纖環內存在大量隨機分布的偏振串擾點，且當環境溫度變化時串擾點的位置和強度均發生變化。因此以往文獻在通過光路模型分析光纖環靜態零偏時與實際情況有所偏差。

本文通過麥克爾遜干涉儀測量光纖環中存在N個串擾點，并得到這些串擾點的位置和強度信息[12]。根據串擾點的位置信息，將2個串擾點之間的光纖長度等效為2個熔接點之間的尾纖長度；根據串擾點的強度信息等效為角度，將串擾點轉化為熔接點。根據上述信息最終建立與溫度相關的光纖環瓊斯矩陣表達式：

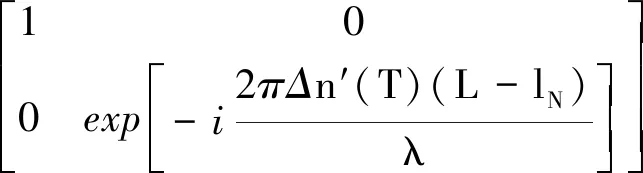
(1)

(2)

式中:TCoil_CW和TCoil_CCW表示光信號在光纖環中順時針和逆時針傳播時的瓊斯矩陣；Δn′(T)=-5.72×10-7T(t)；結合圖1所示，li表示第i個串擾點在光纖環中的位置，其中li+1-li=Li；ln表示光纖環中最后一個偏振串擾點到光纖尾端的位置；L表示光纖環長度；θi表示光纖環中第i個串擾點強度等效的對軸誤差角度。式(1)和(2)中矩陣模型中各元素的值能夠通過實驗設備得到。

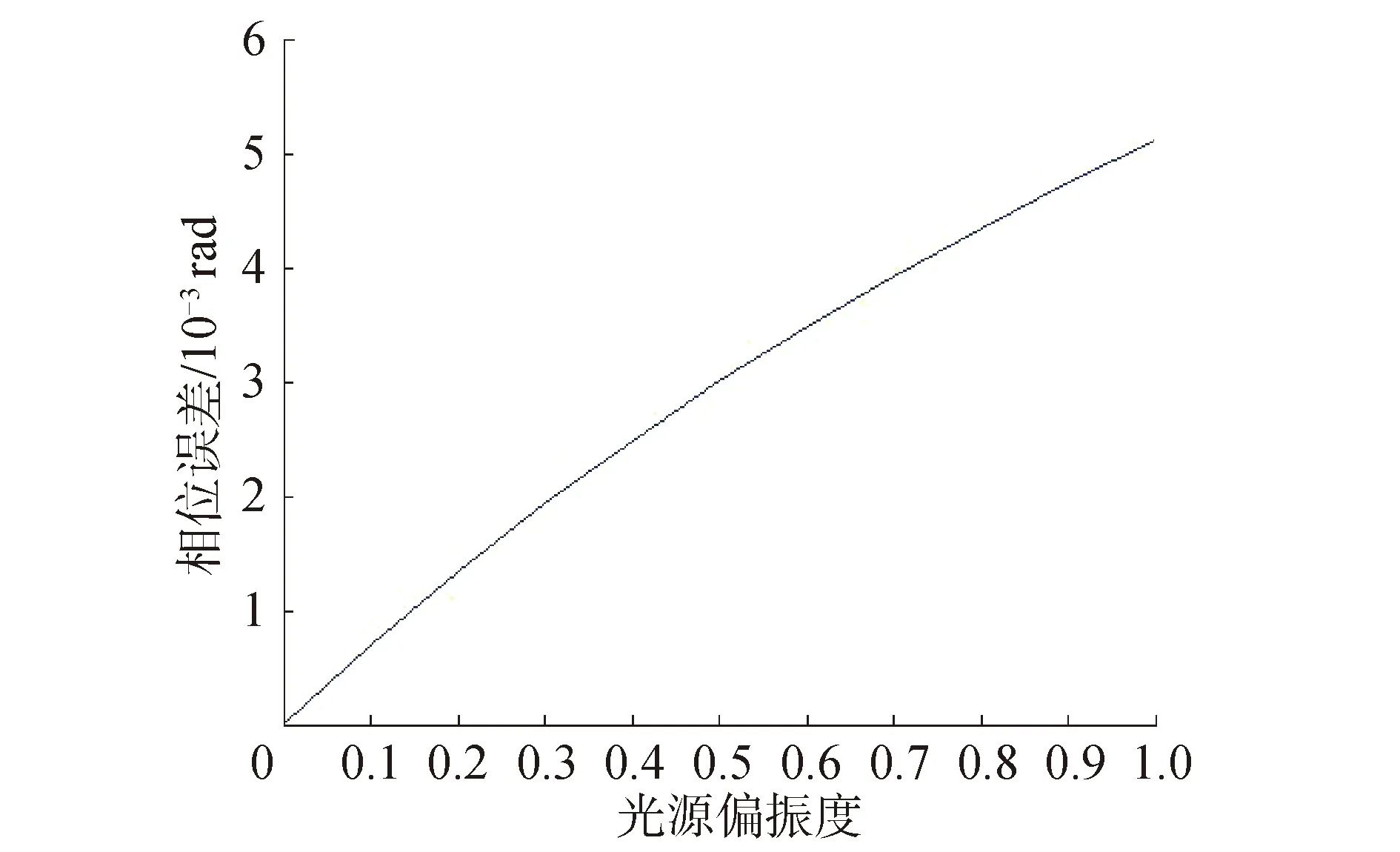
圖1 光源偏振度與偏振串擾相位誤差的關系Fig.1 Changes in the degree of polarization at the FOG output of the phase shift error

由干涉儀的工作原理可知在最大干涉條紋包絡2側對稱位置各出現一個由兩波列產生的干涉條紋，由此計算出偏振光的耦合強度為：

(3)

式中：Icm為干涉次峰包絡的幅值；Im為干涉主峰包絡的幅值。

且當麥克爾遜干涉儀補償引入的相位誤差后，對應的干涉包絡，耦合強度分別為：

(4)

式中β表示起偏角度。當β=0時，干涉峰只剩下h1項，由式(4)可知，耦合光的強度是由對軸角度θ決定的，因此能夠通過串擾強度得到光纖環內串擾點的對軸角度θ。

根據光纖陀螺光路原理圖中光信號傳輸路徑以及上述光路中串聯的各光學器件的瓊斯矩陣，建立光信號在光路中順向和逆向傳播時的瓊斯矩陣分別為：

(5)

(6)

式中：φs表示Sagnac相移，光源和PIN-FET探測器之間的傳輸矩陣為：

G=GCW+GCCW=

(7)

則陀螺輸出光信號的相干矩陣為：

J=GJsourceGH

(8)

探測器檢測到光強為：

IOUT=Tr[JOUT]

(9)

若通過方波調制，即設置相位調制器施加±π/2相位。當光信號傳播至相位調制器時，調制相位滿足：

φm(t)-φm(t-τ)=±π/2

(10)

系統光路輸出光強表示為：

Iout=I0+Nsinφs+Mcosφs=I0+IPsin(φs+φe)

(11)

式中：I0表示輸出光強的常數項;Ip表示偏振串擾導致的光強變化;φe表示由偏振串擾導致的相位誤差，根據式(11)偏振相位誤差可以表示為：

(12)

2 各光學器件偏振串擾仿真及分析

本文以建立的光路模型為依據，結合式(11)和(12)，分析各光學器件的性能對偏振相位誤差的影響。

2.1 光源偏振度P與偏振相位誤差

若不考慮部分損耗和耦合，設光纖耦合器分光比為1∶1，偏振器消光比ε=0.025，光源假定為線偏振光，橢圓方位角ψ=0.1 rad。光源偏振度P與偏振串擾相位誤差φe的關系如圖1所示。

根據圖2仿真結果，當光源偏振度P=0時，對應相位誤差φe=0，且相位誤差φe與光源偏振度P呈近似正比的關系。為減小由于光源偏振度導致的相位誤差可以考慮選用非偏振光源。

圖2 消光比ε與輸出光強Iout的關系Fig.2 The relations between polarization extinction ratio and output light intensity

2.2 消光比與干涉光強

當不考慮光纖陀螺光路中耦合且假設各器件尾纖熔接點無失準角。由于實際情況下Y波導中集成偏振器的消光比ε不可能為零。假設φs表示不同轉速下輸出的Sagnac相移，當φs=π/6，π/3，π/2時，根據光路模型，消光比ε與干涉光強Iout在不同φs時的仿真曲線如圖2所示。

如圖2所示，在同一的轉速下，消光比ε增大，輸出光強Iout也增大且在ε逐漸增大的過程中Iout的增長速度變快。不同轉速下，消光比ε與輸出光強Iout變化規律大體相同。

2.3 光纖環內偏振串擾點等效

通過麥克爾遜干涉儀測量出光纖環中偏振串擾信息，當建立不同溫度下光纖陀螺光路模型時，可以將光纖環中的偏振串擾點等效為纖與纖之間的熔接點，通過已知的偏振串擾強度計算兩段光纖偏振面旋轉角度即對軸角度θ，再根據偏振面旋轉角度對偏振相位誤差的影響進行分析，最終得到偏振相位誤差與偏振串擾強度之間的關系。

通常情況下β=0，故式(3)中串擾強度主要由h1項組成，則h1項串擾強度和對軸角度α之間的關系如圖3所示。

圖3 偏振串擾強度和對軸角度之間的關系Fig.3 The relationship between coupling intensity and alignment angle

根據建立的光路模型和偏振相位誤差表達式(12)，推導出光纖環中偏振串擾強度等效的對軸角度θ與光纖陀螺偏振相位誤差的關系如圖4所示。

圖4 偏振面旋轉角與相位誤差的關系Fig.4 Output error in FOG with the variation of the polarization plane rotation

圖4中的曲線表明，陀螺輸出相位誤差隨偏振串擾強度等效的對軸角度θ的變化，呈近似正比關系，當對軸角度θ=0時相位誤差也為0，綜上光纖環中的偏振串擾強度越小，陀螺輸出偏振相位誤差越小。

3 溫度實驗結果及分析

取實驗室繞制的2個光纖環設置編號為#1和#2，進行高低溫實驗。參考GJB2 426 A-2004[13]，得到在不同溫度時光纖陀螺光路中由于偏振串擾相位誤差而引起的陀螺零偏：

(13)

3.1 偏振串擾測試系統及流程

將待測光纖環放置在溫箱內，設置溫度為-40 ℃～60 ℃勻速升溫，每隔20 ℃，待溫箱溫度穩定后，通過麥克爾遜干涉儀測試并記錄待測光纖環中偏振串擾點位置和強度。表1和表2為統計光纖環1#和2#在不同溫度情況下偏振串擾強度的均值、最大值以及串擾強度大于-40 dB的個數。

表1 不同溫度點下光纖環1#的偏振串擾

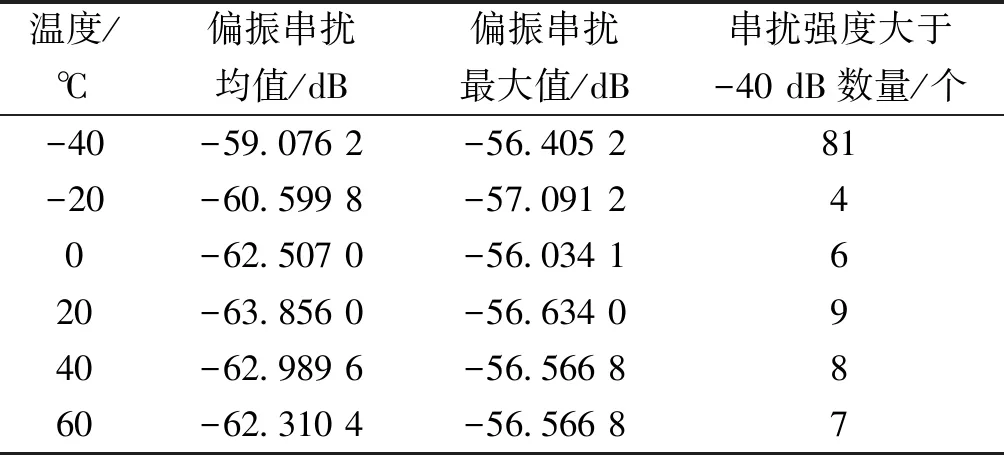
表2 不同溫度點下光纖環2#的偏振串擾

對比表1和表2統計的測試結果，在不同溫度點下光纖環1#和光纖環2#偏振串擾強度的均值和最大值均出現規律性變化，在溫度范圍端點光纖環中出現高串擾點的數目偏高，尤其在低溫-40 ℃時，偏振串擾強度大于-40 dB的個數明顯高于其他溫度。出現該現象是由于，光纖環內部固膠在高溫或低溫情況下發生不可預測的體積變化，導致纖與纖之間出現擠壓，光纖受到應力作用產生高串擾點。

除光纖環外，建立的光纖陀螺光路模型中各光學器件的瓊斯矩陣中的元素，根據實驗室用光纖陀螺的參數進行設置，光源偏振度P=1；輸入光強度為1，Y波導中消光系數ε=0.025，消光比為35 dB；各器件間的尾纖為1 m；光源的波長為1 550 nm；設置光纖環偏振串擾測試溫度為-40，-20，0，20，40，60，將測得的偏振串擾強度和位置的數據，代入光纖環瓊斯矩陣中進行計算。

最終，根據模型得到光纖環1#和2#在不同溫度點下的靜態零偏預估值如表3所示，可以認為光纖環2#在全溫下的性能優于1#。

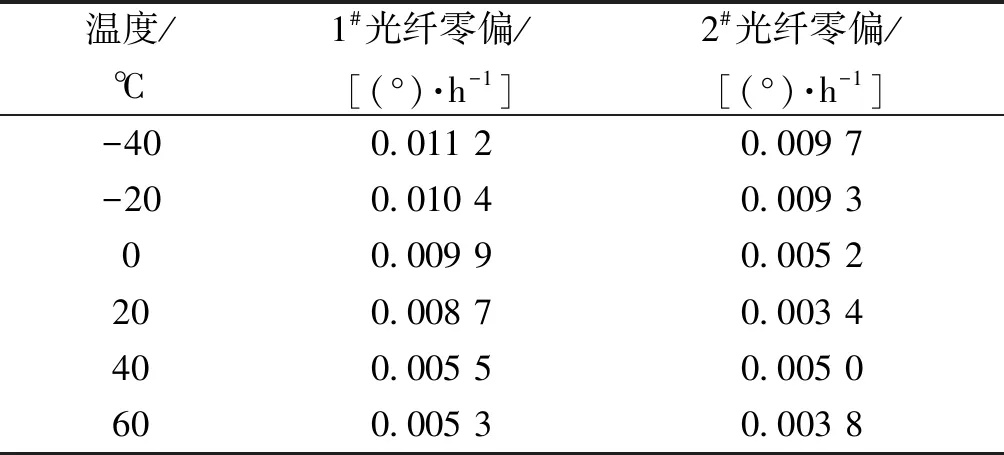
表3 全溫下光纖環1#和2#靜態零偏預估值

3.2 光纖陀螺靜態溫度實驗

3.2.1 溫度對陀螺性能的影響

為了驗證溫度對陀螺性能的影響，將光纖環1#和2#接入光纖陀螺系統。采集常溫(20 ℃)狀態下時陀螺的靜態輸出值，通過式(13)計算光纖環1#和2#的靜態零偏。

表4 光纖環1#和2#的靜態零偏

設置溫箱溫度變化范圍-40 ℃～60 ℃～-40 ℃，變化速率為20 ℃/h。圖6表示溫度勻速變化的情況下陀螺輸出數據隨溫度變化的曲線，通過實驗證明隨著溫度的變化陀螺輸出呈趨勢性變化。

對比表4陀螺靜態零偏，在變溫情況下2個光纖環的靜態零偏明顯高于常溫情況下。通過溫度實驗證明在建立光纖環瓊斯矩陣模型時，引入溫度變化量是正確且必要的。

圖5 陀螺變溫下靜態輸出曲線Fig.5 The relationship between FOG output and temperature variation

3.2.2 全溫度下光纖陀螺靜態輸出采集

設置起始溫度為-40 ℃，每升溫20 ℃待溫箱溫度穩定后，采集該溫度下2 h的光纖陀螺靜態輸出數據，直至升溫到60 ℃。根據獲得的陀螺輸出數據計算出光纖環1#和2#接入的陀螺系統的靜態零偏，如表5所示。

表5 全溫下光纖環1#和2#零偏穩定性實測值

對比表3和表5的數據，光纖環1#和2#預估靜態零偏值和實驗測試靜態零偏值，說明根據建立的光路模型能夠得到與實驗測試靜態零偏較為一致的數據。因此認為根據建立的光路模型得到的預估結果能夠大致反映光纖環接入系統后的實際測試結果，證明了模型具有合理性。根據光纖陀螺溫度實驗得到的數據，光纖環中偏振串擾的均值低，高串擾點少，由此光纖環組成的光纖陀螺靜態性能好，反之靜態性能差。考慮到在光纖陀螺系統中，由于偏振串擾導致的相位誤差僅僅是導致零偏的一部分，預估值小于實測值是合理的。

4 結論

1)光纖陀螺靜態性能在溫度范圍的端點會有所降低；通過光路模型解得的預估值與通過溫度實驗得到的測量值，結果具有線性關系。本文中提到的光纖環瓊斯矩陣模型不僅僅適用于光纖陀螺用光纖環，其他領域用光纖環同樣適用。

2)由于光纖環測量技術的限制，局限于在固定溫度下測量光纖環，因此本文僅針對固定溫度點下光纖陀螺零偏進行分析。缺少光纖陀螺在溫度變化時，由于偏振串擾點位置和強度的變化對陀螺精度的影響分析。

3)建立的光路模型具有準確性和適用性，在實際工程中可以作為一種預先篩選光纖環的手段，用以提高光纖陀螺精度。

4)實驗結論該模型具有準確性和通用性能夠成為評估和優化光纖陀螺靜態性能的理論依據。而要改進光纖環性能，則需選擇保偏光纖、改進繞環技術等方向努力。