訓練深層抽象思維，培養核心數學能力

甘肅 張建文

數學抽象是數學核心素養的重要組成部分，是考查學生數學能力的主要指標.數學抽象是指通過對數量關系和空間形式的抽象，得到數學研究對象的素養.數學抽象的主要表現為:獲得數學概念和規則，提出數學命題和模型，形成數學方法與思想，認識數學結構與體系.

1.數學抽象按照抽象的深度可以分為淺層次抽象和深層次抽象

淺層次抽象是深層次抽象的基礎，只有經歷了淺層次抽象才可以形成深層次抽象，深層次抽象是淺層次抽象發展的必然結果.

1.1淺層次抽象

在具體的實際情境中借助于若干具體的數學原型與實例，通過歸納類比的推理模式得到相關的數學概念或命題.淺層次數學抽象大多在新授課中進行，多在概念教學或命題教學中得到體現.

1.2深層次抽象

規則意識凸顯，結構意圖明了，主要在具體的數學情境中，通過對數學概念和命題的比較分析，得到結構更簡單、表達式更簡潔、應用更廣泛的結論.深層次抽象主要體現在規則和結構這兩個方面，即幾何作圖方面的規則性和操作性以及代數表達方面的簡潔性和結構性.

2.數學抽象是可以通過系統訓練得到發展與提高的，數學抽象思維的訓練具有以下三重境界

2.1由特殊到一般的歸納式訓練

這是數學抽象的正面訓練模式，是最常見、最普遍的訓練方法，也是形成淺層次數學抽象能力的主要渠道.歸納式訓練分為完全歸納和不完全歸納兩種，主要是以不完全歸納為主.通過分析大量實例，從數量與數量關系、圖形與圖形關系以及事物的實際背景中得到一般性的結論.教師主要創設一定的教學情境，引導學生探究討論，最終師生達成共識得到結論.

2.2由一般到特殊的演繹式訓練

這是數學抽象的反饋訓練模式，即利用正面得到的結論去識別或分析具體數學對象.因為通過歸納式得到的一般性的結論具有一定的抽象性，自己建立起來的抽象思維是否正確、思維過程是否科學、結論是否牢固還有待檢驗，所以進行演繹式訓練是對歸納式訓練的有效補充和強化.

2.3透過現象看本質的拔高式訓練

拔高式訓練主要是對規則和結構的升級訓練，是對數學對象的高層次認識，是提高學生創新能力的充分條件.數學抽象結論升華為一定的生活哲理，訓練過程融入自己的情感與感受，是發展學生學習興趣和強化學習動力的主要方式.

2.3.1規則訓練:主要體現在幾何作圖上，目標是從抽象表達式中讀懂對應圖形的結構特點或操作方法，不同的抽象表達式當中蘊藏著不同的圖形操作步驟和方法.根據抽象表達式確定圖形的所有可能情形以及不同的變換方法之間的優劣.

2.3.2結構訓練:主要體現在代數表達式上，通過比較研究抽象表達式結構上的相似性與差異性，求解或構造新的表達式來解決實際問題.如函數解答中的構造函數問題就是最具代表性的結構訓練，這需要學生具備扎實的基礎知識，能對問題有高屋建瓴的把握.

規則性與結構性是深度抽象的兩個重要方面，兩者相輔相成、相互轉化，共同促進學生抽象思維能力的發展.

3.抽象表達式是訓練學生高級思維的主要載體，下面通過對曲線對稱性的研究，在規則和結構方面蘊含的特點進行簡要分類說明.

3.1曲線關于點的對稱

這里的曲線可以是函數圖象，也可以是一般曲線，如橢圓、雙曲線及拋物線等.

曲線f(x,y)=0關于定點M(a,b)的對稱曲線方程為f(2a-x,2b-y)=0.

特別地，曲線f(x,y)=0關于原點O(0,0)的對稱曲線方程為f(-x,-y)=0.

函數y=f(x)關于定點M(a,b)的對稱函數為y=2b-f(2a-x).函數y=f(x)關于原點O(0,0)的對稱函數為y=-f(-x).

3.2曲線關于線的對稱

曲線關于直線的對稱結果仍然是曲線，根據已知曲線和對稱直線(對稱軸)就可以求出新曲線的方程.

3.2.1曲線f(x,y)=0關于x軸的對稱曲線方程為f(x,-y)=0；

3.2.2曲線f(x,y)=0關于y軸的對稱曲線方程為f(-x,y)=0；

3.2.3曲線f(x,y)=0關于直線y=x的對稱曲線方程為f(y,x)=0；

3.2.4曲線f(x,y)=0關于直線y=-x的對稱曲線方程為f(-y,-x)=0；

3.2.5曲線f(x,y)=0關于直線x=a的對稱曲線方程為f(2a-x,y)=0；

3.2.6曲線f(x,y)=0關于直線y=b的對稱曲線方程為f(x,2b-y)=0.

由此可以抽象得到一般的曲線C關于直線對稱的求解方法，即已知曲線C:f(x,y)=0,直線l:ax+by+c=0,下面可求曲線C關于直線l的對稱曲線.

設P(x0,y0)為曲線C上的點，即f(x0,y0)=0.P關于直線l的對稱點為Q(x,y),則有

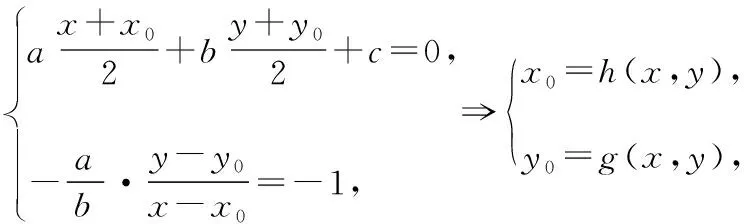
特別地,函數y=f(x)關于定直線x=a的對稱函數為y=f(2a-x).函數y=f(x)關于y軸的對稱函數為y=f(-x).

3.3函數圖象自身的對稱性

函數圖象具有某種對稱性是函數自身的性質，而且是只有某一類特殊函數圖象才具有的性質，比如奇函數與偶函數.而曲線關于點或線的對稱是一種圖象變換方式，這兩者是有顯著區別的.下面對函數y=f(x)的對稱性進行簡單論述.

3.3.1若函數y=f(x)滿足:f(x)+f(2a-x)=2b,則y=f(x)關于點M(a,b)對稱.

特別地,當函數y=f(x)滿足：f(x)+f(-x)=0時,則y=f(x)圖象關于原點對稱,即y=f(x)是奇函數.

3.3.2若函數y=f(x)滿足:f(x)=f(2a-x),則y=f(x)關于直線x=a對稱.

特別地,當函數y=f(x)滿足:f(x)=f(-x)時,則y=f(x)圖象關于y軸對稱,即y=f(x)是偶函數.

3.3.3抽象函數中的奇偶性:

若函數y=f(x+a)為奇函數，即f(x+a)+f(-x+a)=0,則y=f(x)關于M(a,0)對稱.

若函數y=f(x+a)為偶函數，即f(x+a)=f(-x+a),則y=f(x)關于直線x=a對稱.

3.4函數的奇偶性+周期性?對稱性

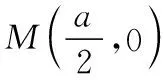
證明:由于y=f(x)為奇函數,所以f(x)=-f(-x).且f(x)=f(x+a)，

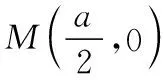
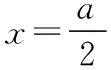
3.5函數的奇偶性+對稱性?周期性

3.5.1若函數y=f(x)為奇函數,且關于點M(a,0)對稱,則y=f(x)為周期函數,且周期T=2|a|(證明如下).

證明:由于y=f(x)為奇函數,所以f(x)=-f(-x).又由于函數關于點M(a,0)對稱,所以有f(2a+x)+f(-x)=0,因此可得f(2a+x)-f(x)=0,即f(2a+x)=f(x).故y=f(x)為周期函數,且周期T=2|a|.

3.5.2若函數y=f(x)為奇函數,且關于直線x=a對稱,則y=f(x)為周期函數,且周期T=4|a|(證明方法類似3.5.1,證明過程略).

3.5.3若函數y=f(x)為偶函數,且關于點M(a,0)(其中a>0)對稱,則y=f(x)為周期函數,且周期T=4|a|(證明方法類似3.5.1,證明過程略).

3.5.4若函數y=f(x)為偶函數,且關于直線x=a對稱,則y=f(x)為周期函數,且周期T=2|a|(證明方法類似3.5.1,證明過程略).

4.訓練學生高級抽象思維的另一種主要手段是進行構造法訓練.通過對抽象函數表達式結構的分析理解,構造恰到好處的新函數解決問題.

4.1根據任意函數構造對稱函數

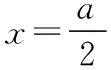
證明:由于F(x)=f(x)+f(a-x)，所以F(a-x)=f(a-x)+f(x)

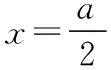
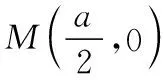
4.2根據任意函數構造分段對稱函數

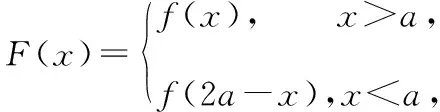
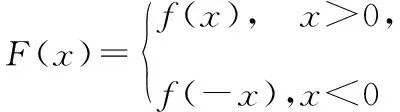
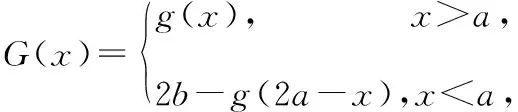
4.3根據導數具體形式構造函數

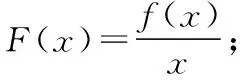
4.3.2已知y=f(x)滿足:xf′(x)+f(x)<0，則可構造F(x)=xf(x).

構造法的應用在不同的實例當中有不同的表現形式，具體問題具體分析，不可一概而論.

5.典例賞析

5.1關于線的對稱應用

【例1】(2015·全國卷Ⅰ·文12)設函數y=f(x)的圖象與y=2x+a的圖象關于直線y=-x對稱，且f(-2)+f(-4)=1,則a=

( )

A.-1 B.1

C.2 D.4

【分析】此題明顯屬于曲線關于直線對稱類問題,已知曲線C1:y=2x+a,曲線C1關于直線y=-x的對稱曲線是C2:-x=2-y+a，即y=-log2(-x)+a,可得f(x)=-log2(-x)+a，

代入式子f(-2)+f(-4)=1，可得a=2.

( )

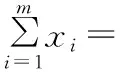
A.0 B.m

C.2mD.4m

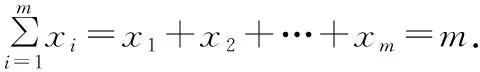
【小結】例1需要求出對稱曲線的方程，是兩條曲線關于直線的對稱問題，例2則要從抽象表達式中讀出曲線的對稱軸，是函數圖象自身具有對稱性.此兩例堪稱是關于直線對稱的典范，其中包含的解答思路與方法具有很強的擴展性和普遍性.

5.2關于點的對稱應用

( )

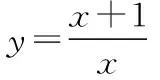
A.0 B.mC.2mD.4mm

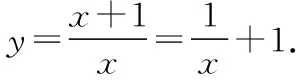
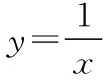
【小結】此例是關于點對稱模型的經典應用,和例2非常類似,都屬于函數本身具有的對稱性質.

5.3對稱性與奇偶性的結合

【例4】(2018·全國卷Ⅱ·文12)已知f(x)是定義域為(-∞,+∞)的奇函數，滿足f(1-x)=f(1+x).若f(1)=2，則f(1)+f(2)+f(3)+…+f(50)=

( )

A.-50 B.0

C.2 D.50

【分析】因為y=f(x)為奇函數,且圖象關于直線x=1對稱,所以f(x)的周期T=4.又由于f(0)=0,f(1)=2,f(2)=f(1+1)=0,f(3)=f(-1)=-f(1)=-2,f(4)=0,

所以f(1)+f(2)+f(3)+…+f(50)=12(f(1)+f(2)+f(3)+f(4))+f(1)+f(2)=2.

【小結】此題的解答關鍵在于根據已知條件得到f(x)的周期T=4,之后的求值計算就會迎刃而解,所以在理解與計算過程中要抓主抓重.

5.4構造對稱函數

【例5】(2017·全國卷Ⅰ·文9)已知函數f(x)=lnx+ln(2-x)，則

( )

A.f(x)在(0,2)單調遞增

B.f(x)在(0,2)單調遞減

C.f(x)的圖象關于直線x=1對稱

D.f(x)的圖象關于點(1,0)對稱

【分析】根據任意函數構造對稱函數的方式可得，f(x)的圖象關于直線x=1對稱.

5.5導數中的構造法

【例6】(2015·全國卷Ⅱ·理12)設函數f′(x)是奇函數f(x)(x∈R)的導函數,f(-1)=0,當x>0時,xf′(x)-f(x)<0,則使得f(x)>0成立的x的取值范圍是

( )

A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)

C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)

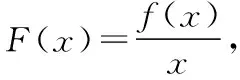
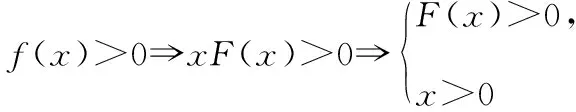
【小結】抽象函數的構造源于對式子的精準理解和獨到把握,更需要提升深層抽象能力，從相似元素中找差異，從不同元素中找共性.

6.總結與展望

以上是筆者對數學抽象素養的一個側面進行的論述，論述主要是以抽象函數的對稱性為研究對象展開的，對抽象函數的對稱性進行了多層次多角度的簡單論述，希望對培養學生的抽象思維能有所幫助.在新課改的大潮流下，深入理解學生、理解教學都需要我們從全新的視角思考問題,做到因材施教、順勢而為,運用各種方式提高教與學的效率.