深度學習理念下數學教學錯題錯解歸類例析

湖北 周 威

數學是一門思維嚴謹的學科.然而，在高中數學解題教學或模擬考試中，由于缺乏思維嚴謹性導致一些錯題或錯解出現，對解題教學和學生學習造成了一定的負面影響.本文所說的錯題是指有邏輯錯誤的題,錯解也是指在解題過程中由于邏輯不嚴謹、不合情理導致的錯誤解答.正所謂“失敗乃成功之母”，錯題與錯解也有其教育價值及教育功能.對錯題與錯解的歸類例析，是提升學生邏輯推理核心素養的有效途徑，也是深度學習的表現.黎加厚教授曾經指出，深度學習意味著理解和批判，意味著聯系和構建，意味著遷移與應用.本文基于深度學習的特點歸類例析筆者最近教學研究中遇到的一部分典型錯題與錯解，與讀者交流.

1. 充分、必要、充要條件混淆導致錯題與錯解

【例1】已知f(x)為R上的偶函數，滿足f(x+1)=-f(x),且當x∈[0,1]時，f(x)=3x-1，則函數g(x)=f(x)-log2|x|的零點個數是( )

A.2 B.4 C.6 D.8

似乎正確的解析：由題意知f(x+2)=-f(x+1)=f(x),所以f(x)的周期為2，又由于x∈[0,1]時，f(x)=3x-1，且f(x)為R上的偶函數，利用數形結合可畫出y=f(x)與y=log2|x|的函數圖象，觀察可得其交點個數為6個，故選C.

點評：整個解題過程條件應用到位，運用了化歸與轉化、數形結合思想，似乎十分合理，但是，仔細斟酌就會發現，若取x=0,根據題設條件f(x+1)=-f(x)得f(1)=-f(0)，代入條件“當x∈[0,1]時，f(x)=3x-1”，于是會得到“0=2”的矛盾結果！因此，這是一道錯題！因為解題過程中起作用的是“函數f(x)的周期為2”，但條件“f(x+1)=-f(x)”是“f(x+2)=f(x)”的充分不必要條件，也就是說這兩個條件并不等價！

【例2】已知函數f(x)=lnx+ax的圖象存在與直線2x-y=0平行的切線，則實數a的取值范圍是________.

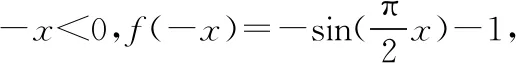
2. 恒成立與最值問題混淆導致錯題

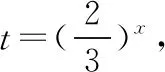
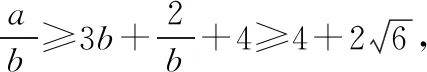
3.不等式放縮不嚴謹導致錯題

A.(1,+∞) B. (e,+∞)

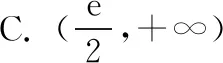
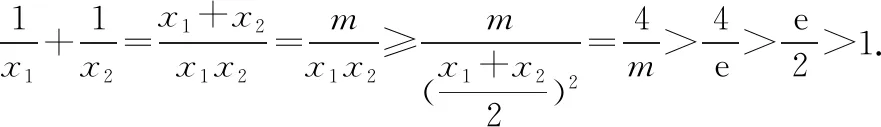
4.沒有把握數學本質的答案巧合導致錯解

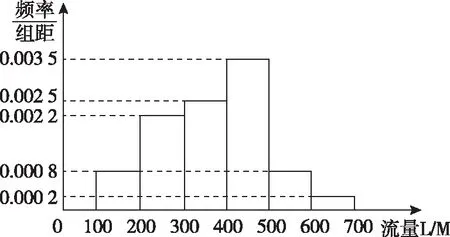
【例6】某學校為鼓勵家校互動,與某手機通訊商合作,為教師辦理流量套餐,為了解該校教師手機流量使用情況,通過抽樣,得到100位教師近2年每人手機月平均使用流量L(單位：M)的數據，其頻率分布直方圖如下.若將每位教師的手機月平均使用流量分布視為其手機月使用流量，并將頻率視為概率，回答以下問題.

(1)從該校教師中隨機抽取3人，求這3人中至多有1人月平均使用流量不超過300M的概率；

(2)現該通訊商推出三款流量套餐，詳情如下：

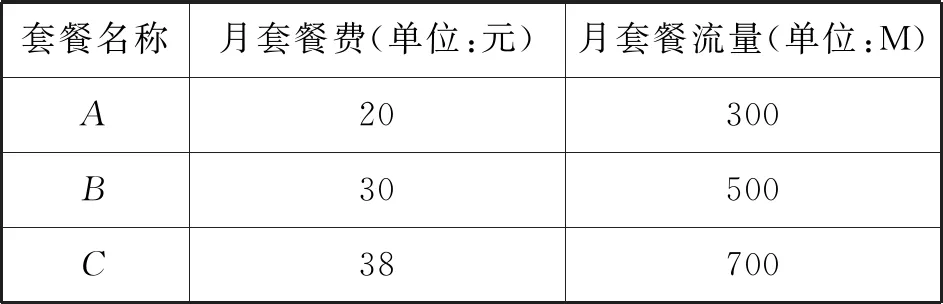
套餐名稱月套餐費(單位:元)月套餐流量(單位:M)A20300B30500C38700

這三款套餐都有如下附加條款：套餐費月初一次性收取，手機使用一旦超出套餐流量，系統就自動幫用戶充值200M流量，資費20元；如果又超出充值流量，系統就再次自動幫用戶充值200M流量，資費20元/次，依此類推，如果當月流量有剩余，系統將自動清零，無法轉入次月使用.

學校欲訂購其中一款流量套餐，為教師支付月套餐費，并承擔系統自動充值的流量資費的75%，其余部分由教師個人承擔，問學校訂購哪一款套餐最經濟實惠?說明理由.

錯解：(2)由頻率分布直方圖可知每位教師手機月平均使用流量為x=150×0.08+250×0.22+350×0.25+450×0.35+550×0.08+650×0.02=369(M).

也就是說,該校每位教師手機月平均使用流量為369M,以下分三種情況：

①當學校訂購A套餐時,該校為每位教師承擔的月費用為20+20×75%=35元；

②當學校訂購B套餐時，該校為每位教師承擔的月費用為30元；

③當學校訂購C套餐時,該校為每位教師承擔的月費用為38元.

因為30<35<38,所以學校訂購B套餐最經濟實惠.

點評:此題正確答案是訂購B套餐最經濟實惠.之所以錯解就是沒有抓住問題的本質“數學期望”.事實上，上述“錯解”其實已經沒有在概率統計范疇中考慮問題了，因為學校為每位教師選擇套餐類型，這是個隨機事件，而上述錯解的解答過程，卻把選擇每一類套餐的事件當成必然事件.所以正確解法應當計算出“每類套餐支付費用”的分布列，求出數學期望，根據數學期望值來選擇方案.另外當修改相關數據且套餐只有兩類時，按上述“錯解”的思路也無法算出哪種方案最經濟實惠.

5. 結語