關注數學本質,落實核心素養的培養
——由2020年北京高考數學解析幾何問題引發的思考
北京 王長友
解析幾何綜合問題是高中數學教學的重點,同時是學生學習的難點,更是高考考查的重要載體,本文對學生在2020年北京高考數學解析幾何大題中的完成情況、未完成原因等事實基礎上進行教學思考,希望通過對學生存在的問題進行分析,從而改進教師的日常教學,建立 “追根溯源,關注數學本質”的教學基石.
一、典型問題再現
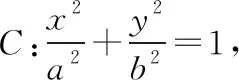
(Ⅰ)求橢圓C的方程;


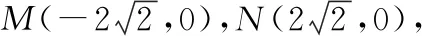
(2)當直線l的斜率不為0時,設直線l的方程為y=k(x+4),易知斜率k存在;設M(x1,y1),N(x2,y2),P(-4,yP),Q(-4,yQ).

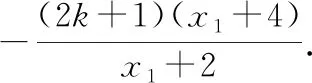

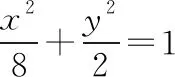
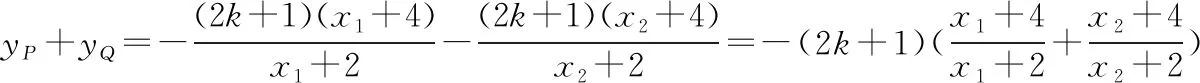


方法二:同方法一的前半部分,即
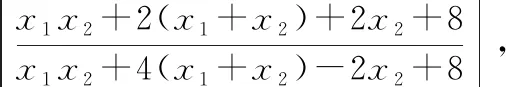
方法三:將原問題轉化為“過點A作兩條直線AM,AN與橢圓交于M,N兩點,且滿足B,M,N三點共線”.
設直線AM的方程為y+1=m(x+2),直線AN的方程為y+1=n(x+2),易知m,n存在且m≠0,n≠0,m≠n.設M(x1,y1),N(x2,y2),P(-4,yP),Q(-4,yQ).
令x=-4,則yP=-2m-1,yQ=-2n-1,
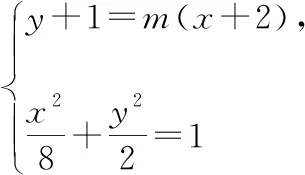


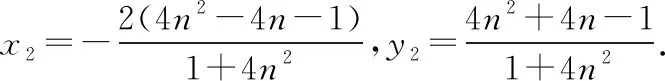



化簡并整理得m2-n2+m-n=0即(m-n)(m+n+
1)=0因為m≠n,所以m+n=-1,
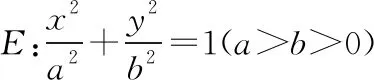
(Ⅰ)求橢圓E的方程;
(Ⅱ)是否存在常數λ,當直線l變動時,總有k1=λk2成立?若存在,求出λ的值;若不存在,說明理由.

方法一:由(Ⅰ)知,A(-2,0),B(2,0),當直線l的斜率不存在時,即直線l的方程為x=1.
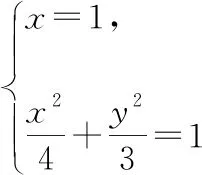

當直線l的斜率存在時,設直線l的方程為y=k(x-1),
C(x1,y1),D(x2,y2).

方法二:設C(x1,y1),D(x2,y2),直線lAC:y=k1(x+2),直線lBD:y=k2(x-2),易知k1,k2存在且都不等于0.

12) = 0,
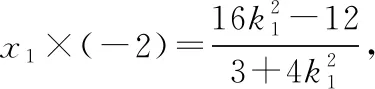


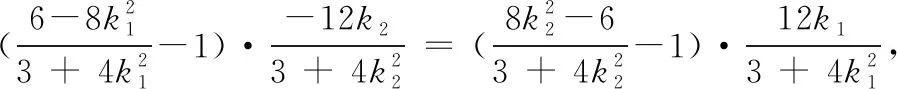

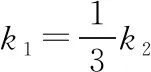

方法三:①當直線l的斜率不存在時,直線l的方程為x=1.
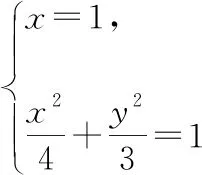
②當直線l的斜率存在時,設直線l的方程為y=k(x-1),顯然k≠0,C(x1,y1),D(x2,y2).

方法四:①當直線l的斜率不存在時,同方法三;
②當直線l的斜率存在時,設直線l的方程為y=k(x-1),顯然k≠0,C(x1,y1),D(x2,y2).

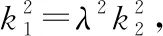

整理得 4(1-λ2)-2(1+λ2)(x1+x2)+(1-λ2)x1x2=0,

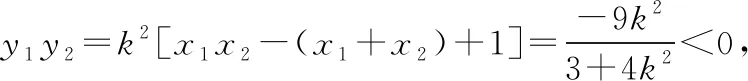

通過對比就會發現,兩個問題研究的方法基本如出一轍,而例2是作者在教學中重點講解的問題,但是在高考中部分學生還是未能很好地順利完成,引人思考.
二、學生困難與剖析
通過調研部分未能整體完成此題的學生,發現基本困難如下:


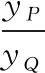

【困難4】學生在實際運算中只求得yP=
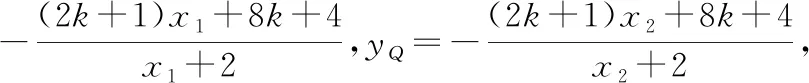
【困難5】對于方法三學生的問題有:未想到上述方法三中的轉化研究對象,想到轉化但是擔心直線與橢圓方程聯立時運算量大不敢實施,或部分實施后未能明確運算方向為研究m,n的關系,在實施過程中出現運算錯誤造成無法完成等.
進一步對學生困難進行挖掘、分析,可以發現學生困難的本質,一方面學生未能用數形結合思想、運動變化觀點、特殊與一般的關系,主動探究解決問題的思路;另一方面學生對解析幾何中運算的方向、策略,運算的方法與經驗等不理解,缺少理性思考與感悟.因此,可以得出的基本結論為:很多學生的解析幾何學習是“習慣在高度模仿水平”,未能理解解析幾何學習的本質.
三、教學思考
分析高考真題與學情,結合教育部關于高考的主要任務為:立德樹人“一堂課”、服務選才“一把尺”、引導教學“一面旗”的要求,教師的日常教學需要進行深刻反思,在教學中抓住數學本質、落實學科素養的培養.
(一)解析幾何教學的本質與學業要求
教師要明確新課標指出的解析幾何是“研究對象是幾何圖形,研究方法主要是代數方法”的教學本質,認真研讀新課標關于解析幾何的學業要求,即“根據具體問題情境的特點,建立平面直角坐標系;根據幾何問題和圖形的特點,用代數語言把幾何問題轉化為代數問題;根據對幾何問題(圖形)的分析,探索解決問題的思路;運用代數方法得到結論”.
(二)思考
按照課標要求,對比學生在上述解答問題中出現的困難,就清晰地指明了教師在教學中的改進方向.
1.教師要重視基礎知識、基本技能、基本思想與方法、基本學習經驗的生成過程
在教學過程中,教師要敢于給學生思維的時間與空間,充分體現學生探究、困惑、優化、解惑的過程,只有充實過程,才能感悟深刻.教師在教學中應該引導學生充分理解:解析幾何綜合問題是在運動變化過程中研究變化規律(確定性質、特殊規律等),因此抓住研究對象間的聯系合理轉化為代數關系是核心,有效進行運算、解決問題是落腳點,教師要科學、有層次的設計問題,進而引導學生逐步建立良好的研究解析幾何問題的思維過程,即

簡而言之,分為三個過程,即學生認識與體會、理解與正確操作、掌握與感悟本質.
2.教師要系統規劃與細化解析幾何運算素養提升的途徑
解析幾何研究的運算對象較多,教學中需要引導學生從幾何、代數等基本關系入手,尋找連接點,合理設計與選擇運算方法, “算什么、怎么算”是解析幾何運算素養落地的核心.解析幾何的運算分為兩方面,一方面是常規程序化運算(如直線與曲線方程聯立、共線、垂直、平行等位置關系的求解等),另一方面為結合問題情境自主設計運算.程序化運算是基礎,要指導學生落實細節并養成良好的運算習慣(如例1運算過程中隨時化簡的習慣等);自主設計是目標,要充分理解運算的本質是邏輯推理分析,要讓學生學會定性與定量的結合,關注定性分析明方向、關注定量運算求準確;要有時刻進行化繁為簡的意識;要有效進行整體代換,重視運算結構;大膽實施估算與精算的有機結合等.
3.教師要引導學生主動思考與激發學生的創造性
回顧例1中的北京高考試題和例2的模擬題,進一步分析會發現問題的共性為:與橢圓有關的兩條直線的斜率具備特殊關系(如和是定值、差是定值、積是定值、商是定值)時橢圓具有的一些性質.
教師要有意識的設計問題刺激學生.進一步思考就會發現問題表面上是在研究圖形的幾何性質,深層次是數學的邏輯關系使然,是引導學生學會嘗試“用數學的眼光觀察世界、用數學的思維思考世界、用數學的語言表達世界”的數學教育價值,同時學生也能體會到數學的邏輯美、奇異美.只要教師在教學中引領學生主動思考,就會激發學生的創造性.


