借助思維導圖促進高考數學復習

盛琪

摘要：高中數學概念以及相關公式較多，高考復習教學中，應采取一定的策略，不斷提高學生的復習效率，幫助學生在構建系統知識網絡的同時，深化對所學知識的理解，爭取在高考中取得理想的成績。思維導圖能直觀展示高中數學相關知識，給學生留下深刻印象，獲得事半功倍的復習效果。因此高考數學復習教學中，應注重思維導圖的應用，促進學生復習體驗與復習效率的雙重提升。

關鍵詞：高考數學 ?思維導圖 ?復習

思維導圖是一種圖像式的思考輔助工具，可使學習者清晰地看到學習的重點，幫助其厘清知識點之間的內在關聯，使其在頭腦中形成清晰的印象，大大降低復習的枯燥感，獲得預期的復習效果。高考數學復習中，應認識到思維導圖的重要作用，積極采取有效策略，將思維導圖應用于數學復習。

一、借助思維導圖，構建知識網絡

高考數學復習中，使用思維導圖讓所學的數學知識串聯起來，構建系統的知識網絡，幫助學生夯實所學，是高考數學復習的重點。為獲得預期的復習效果，應認真落實以下內容：一方面，課堂上先由學生自主回顧所學的數學基礎知識，把握學習的重點與難點，尤其要引導學生及時回歸課本，清楚數學知識的來龍去脈，明確知識點之間的內在聯系;另一方面，教師要與學生一起圍繞某一重點知識，邊與學生積極互動邊繪制相關的思維導圖，使學生感受思維導圖的繪制過程，在頭腦中形成清晰的印象，將所學的知識點串聯成網，為靈活應用打好基礎。

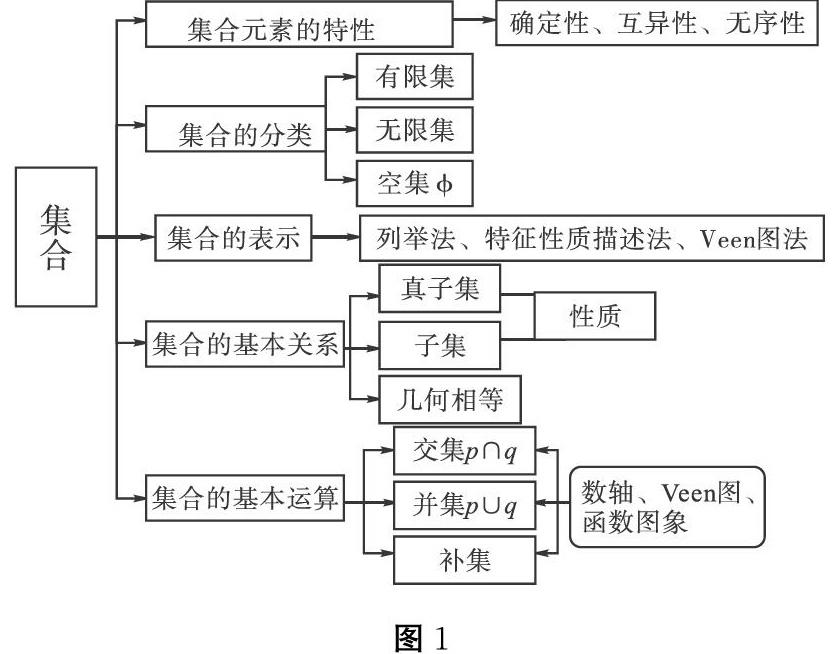
高考數學中有關集合知識的考查較為簡單。復習教學中可借助思維導圖將集合相關知識串聯起來，幫助學生構建系統的知識網絡。繪制思維導圖時可將“集合”作為關鍵詞，而后分別列出集合元素的特性、集合的分類、集合的表示、集合的基本關系與基本運算，再分別繪制其下層包含的知識，將整個集合知識以網絡的形式呈現給學生，如圖1所示。

另外，復習中基于圖1所示的思維導圖，可要求學生沿著各分支，積極回想相關的細節，進一步完善集合知識架構，如針對空集，不僅要明白空集的定義，認識到空集為任何非空集合的真子集，而且還要想到一些結論，如，含有n個元素的集合有2n個子集，2n-1個真子集，以快速地解答相關習題。實踐表明，借助思維導圖構建知識網絡，給學生帶來視覺上的沖擊，能很好地激發學生的復習積極性，提高學生的復習效率，使學生切實掌握基礎知識。

二、借助思維導圖，牢記相關公式

高中數學有很多重要的公式，如對數函數的運算公式、正弦余弦定理、立體幾何中相關參數的向量計算公式等。這些公式是解答數學問題的重要依據，其重要性不言而喻。高考數學復習中應注重運用思維導圖，使學生準確記憶相關公式以及相關公式的變形，能夠做到以不變應萬變。一方面，以某一章節為復習單位，先列出思維導圖的關鍵詞，而后要求學生根據關鍵詞進行充分的聯想，逐一默寫出相關的計算公式。同時，要求同桌之間相互檢查，看默寫的公式是否正確，及時糾正出現的錯誤。另一方面，教師要對繪制的思維導圖進行整理，對相關細節進行優化，而后打印出來，分發給學生，要求學生結合自身實際，加以有針對性的復習，保證相關公式記憶的正確性。

例如立體幾何知識復習中，教師于給出“空間角”“空間距離”等關鍵詞，要求學生回想運用向量知識求解相關參數的公式，在課堂上要求學生默寫，而后進行整理，優化后，繪制如圖2所示的思維導圖，幫助學生更好地記憶。

從圖2的思維導圖中可以清晰地看到可運用向量求解異面直線所成的角、直線與平面所成的角、兩面角以及對應的計算公式。另外，使用向量還可以求解空間距離。復習中除要求學生按照思維導圖認真記憶相關的計算公式外，還應引導學生回顧所學，清楚上述公式中各參數表述的含義，并嘗試著對圖中的公式進行推導，能夠結合具體的問題，應用對應的公式進行計算，避免張冠李戴，以不斷提高學生空間立體幾何問題的解題效率。

三、借助思維導圖，傳授解題思路

高考數學復習中，除運用思維導圖幫助學生夯實基礎知識外，還可運用思維導圖總結與傳授相關的解題思路，使學生遇到類似題型時能夠迅速解答。一方面，教師應認真分析近年來的高考試題，對常考的題型加以匯總，在課堂上與學生一起分析，使其掌握各題型的命題規律，給學生的復習提供指引，提高其復習的針對性。另一方面，教師應引導學生圍繞高考中的常見題型以及解題思路繪制思維導圖，使其繪制的思維導圖不僅能明確地列出各題型的考查知識點，還能列出對應的解題思路、破題技巧等，幫助學生在解答類似問題時少走彎路。

促使學生熟練掌握相關題型的解題思路是高考數學復習工作的重點。教師在復習教學中應圍繞重點知識，借助思維導圖，傳授與歸納相關的解題思路。例如，數列是高中數學的重點知識，求解數列的通項公式以及前n項和是高考的常考題型，復習時可應用思維導圖向學生展示不同題型的解題思路。如針對an+1-an=f（n）遞推類型的習題，可使用逐差累加法求解通項公式。針對an+1=pan+q遞推類型的習題，求解通項公式時可構造等比數列an+qp-1。

高考數學復習中，借助思維導圖向學生展示相關的解題思路，可使學生掌握相關習題的解題技巧，避免走進解題誤區，迅速找到解題思路，促進學生學習能力的提升。

四、借助思維導圖，拓展復習內容

高考數學復習中為更好地提高學生的分析能力以及解題能力，教師應引導學生借助思維導圖積極拓展復習內容，促使學生在扎實掌握所學知識的同時，能進一步拓寬視野，更好地運用數學知識解答各類數學問題。一方面，教師在復習中應要求學生不滿足于已學知識，圍繞所學知識對相關知識點進行深挖，推導相關結論，掌握相關結論的應用注意事項。另一方面，教師引導學生應用思維導圖將拓展的內容加以整理，幫助學生更好地記憶。同時為使學生更好地掌握拓展內容，還可圍繞思維導圖設計相關的習題，要求學生在復習中思考、作答，使學生在解答習題中深化認識與理解。

在進行橢圓知識復習時，要求學生不僅掌握橢圓的定義、標準方程，而且還應借助思維導圖對相關內容進行拓展。如在思維導圖中為學生展示下面的拓展結論：對于標準方程為x2a2+y2b2=1的橢圓，其內部存在一點M（x0，y0），則被M所平分的中點弦的方程為x0xa2+y0yb2=x20a2+y20b2。顯然在思維導圖中通過展示一些常用的結論，能很好地拓展學生的知識面，提高學生的解題效率。

實踐表明，復習中借助思維導圖對橢圓中的內容進行拓展，不僅加深了學生對橢圓知識的認識與理解，提高了復習效率，而且運用拓展的知識更加有助于學生解答相關習題，更好地提升其解題水平。

五、總結

思維導圖是當前在教育領域應用較為廣泛的工具，在提高學習以及復習效率上效果顯著，因此高考數學復習中應提高思維導圖應用意識，認真總結以往授課經驗，尋找高效的策略。復習中教師應充分運用思維導圖構建知識網絡、傳授解題思路、拓展復習內容，促進高考數學復習工作水平的提升，促使學生考上理想的大學。

參考文獻：

[1]蔣鳳.淺談思維導圖在高中數學教學中的應用[J].才智，2019（31）：212.

[2]崔海東.思維導圖在高中數學教學中的應用探究[J].中學數學教學參考，2019（27）：71-72.

[3]張理科.思維導圖在數學教學中的應用[J].中學數學教學參考，2019（24）：68-69.

[4]李鵬翔.“思維導圖”在高中數學教學中的應用[J].數學教學通訊，2019（12）：56-57.

[5]林勇軍.思維導圖在高中數學教學中的應用[J].數學學習與研究，2018（14）：16-17.