基于遺傳算法的函數級別軟件錯誤定位

黃晴雁，牟永敏，崔展齊，張志華

1.北京信息科技大學 計算機學院，北京100101

2.北京信息科技大學 網絡文化與數字傳播北京市重點實驗室，北京100101

1 引言

軟件調試在軟件開發中扮演了極其重要的角色，而快速準確地找到程序中的錯誤是軟件調試的關鍵[1]。手工調試方法耗時耗力且效率低下，為了能夠高效準確地定位軟件錯誤的位置，研究人員提出了很多行之有效的自動化軟件錯誤定位方法。自動化軟件錯誤定位方法分為靜態分析和動態分析兩類。靜態分析方法[2-3]不需運行程序，通過分析程序的源代碼和結構等信息定位到具體的錯誤源；動態分析方法[4]通過運行程序分析測試用例的執行軌跡以及運行結果來輔助定位錯誤位置。

動態分析是自動化軟件錯誤定位研究的重點，大致可以分為基于程序頻譜、基于依賴關系、基于數據挖掘以及基于程序切片的錯誤定位等方法[3-6]。其中，基于程序頻譜的錯誤定位是目前主流的研究思路[7]，通過執行大量測試用例得到程序實體覆蓋信息和執行結果，使用統計學方法計算實體的可疑值，對具有單一錯誤的程序表現出良好的定位效果。Jones 等[8]提出了Tarantula 可疑度計算公式，認為被更多的失敗測試用例執行到的實體，其含有錯誤的可能性要高于其他實體。隨后，Abreu等[4]根據聚類分析提出了Jaccard 公式，受分子生物學啟發提出了Ochiai可疑度計算公式，提高了錯誤定位的效果。Wong等[9]在Kulczynski系數的基礎上提出了DStar方法，實證研究中發現該方法的定位效果要優于其他方法。

近年來，基于搜索的軟件工程（Search Based Software Engineering，SBSE）逐漸被應用于軟件錯誤定位和錯誤自動修復領域[10-12]。SBSE 將傳統軟件工程問題建模為組合優化問題，利用元啟發式搜索技術搜索求解。基于此，張蓓等[13]提出了一種基于增強遺傳BP神經網絡的軟件錯誤定位方法，在效率和精確度上均有進步。王贊等[14]提出了一種基于遺傳算法的多缺陷定位方法，對多缺陷定位問題進行建模，有效減少了人工交互。

目前，大多數的錯誤定位方法針對語句級別，很少基于函數粒度進行研究。語句級別的定位是一種細粒度的定位方法，可以將錯誤定位到某一條語句。然而在實際軟件開發過程中，軟件錯誤的發生大多是由于某個函數內部的邏輯或語句順序出現錯誤造成的。在粗粒度的函數級別上進行錯誤檢測定位比細粒度的語句級別更為合理有效。同時，在程序較為復雜，并且存在多個錯誤位置時，基于搜索的軟件工程能夠提供良好的定位結果。而遺傳算法作為主流的搜索算法，具有很強的通用性、魯棒性和全局搜索能力。因此，本文提出一種基于遺傳算法的函數級別軟件錯誤定位框架FGAFL，通過執行測試用例得到函數級別的程序頻譜，借助基于搜索的軟件工程思想進行建模，結合函數間的調用信息，利用遺傳算法搜索求解。

2 相關概念與技術

2.1 軟件錯誤定位

基于程序頻譜的錯誤定位就是根據程序運行的頻譜信息來統計程序中各個實體的可疑值并進行排序，越可疑的實體含有錯誤的可能性越大[15]。接下來對相關概念依次給出定義，并在之后的內容中采用本節定義的符號概念。

定義1 測試用例集：T={t1,t2,…,tm}表示待測程序的m 個測試用例集合。其中ti表示第i 個測試用例。根據運行結果將T 分為失敗測試用例集TF和成功測試用例集TP。

定義2 待測程序實體集：E={e1,e2,…,en}表示待測程序中包含n 個函數。其中ei表示程序中第i 個函數。

定義3 覆蓋矩陣：M=(Mij)表示測試用例集T 和程序實體集E 之間的覆蓋關系。 M 是一個由0和1構成的m×n 階矩陣。當Mij=1 時，表示測試用例i 覆蓋了函數j，當Mij=0 時，表示測試用例i 未覆蓋函數j。MF=(Mij)是失敗測試用例覆蓋矩陣，包含失敗測試用例集TF的覆蓋信息；MP=(Mij)是成功測試用例覆蓋矩陣，包含成功測試用例集TP的覆蓋信息。

定義4 測試用例結果向量：R={r1,r2,…,rm}表示測試用例集中m 個測試用例的測試結果。其中ri表示第i 個測試用例的執行結果，ri的取值為0或1，當ri=1時，表示第i 個測試用例執行失敗，當ri=0 時，表示第i個測試用例執行成功。

2.2 函數調用路徑

在錯誤定位分析的過程中，文獻[16]提出了軟件錯誤關聯的思想，即失效相關性。在此基礎上，本文認為各個函數之間具有直接或間接的關聯關系，一個有錯誤的函數往往會影響到與之關聯的函數，對找到真正的錯誤根源會造成一定的干擾。為了解決這一問題，本文在函數調用路徑（Function Call Path，FCP）的基礎上進行錯誤定位，在一定程度上減少函數間的關聯對錯誤定位造成的干擾。

以函數為基本單位，把程序的一次執行軌跡描述為一條函數調用路徑，實際上是程序中基于函數調用并且結合數據流、控制流的一種函數執行路徑的靜態描述集合[17]。下面給出函數調用路徑的相關定義。

定義5 函數調用路徑：W 是基于函數調用的一條完整的程序執行路徑，表示為Wi={vi0,vi1,…,vim}，路徑中的相鄰節點表示函數之間的調用或順序執行關系。

整個程序的函數調用路徑的合集組成函數調用路徑圖，與函數調用圖不同的是函數調用路徑圖展示了函數之間的調用與順序執行的關系，而函數調用圖僅分析了函數之間的調用關系，忽略了控制流、數據流等信息。函數調用圖與函數調用路徑圖的對比如圖1所示。

圖1中的源程序包括四個函數：main、f1、f2、f3。其中main函數調用了f1、f2、f3三個函數。圖（a）中函數調用圖沒有考慮調用這些函數時的控制流信息，不能正確反映函數可能的執行路徑，而圖（b）中函數調用圖可以更為準確地反映出該程序中存在的函數執行路徑，路徑1(main →f1→f2→end)和路徑2(main →f1→f3→end)。

2.3 遺傳算法

遺傳算法（Genetic Algorithm，GA）是一類仿生型優化算法，由Holland[18]于20 世紀70 年代提出。該算法模擬生物界“優勝劣汰”的進化過程，是目前主流的啟發式搜索算法之一。基于遺傳算法的技術已經被用于解決函數優化、機器學習、人工智能等領域的問題。

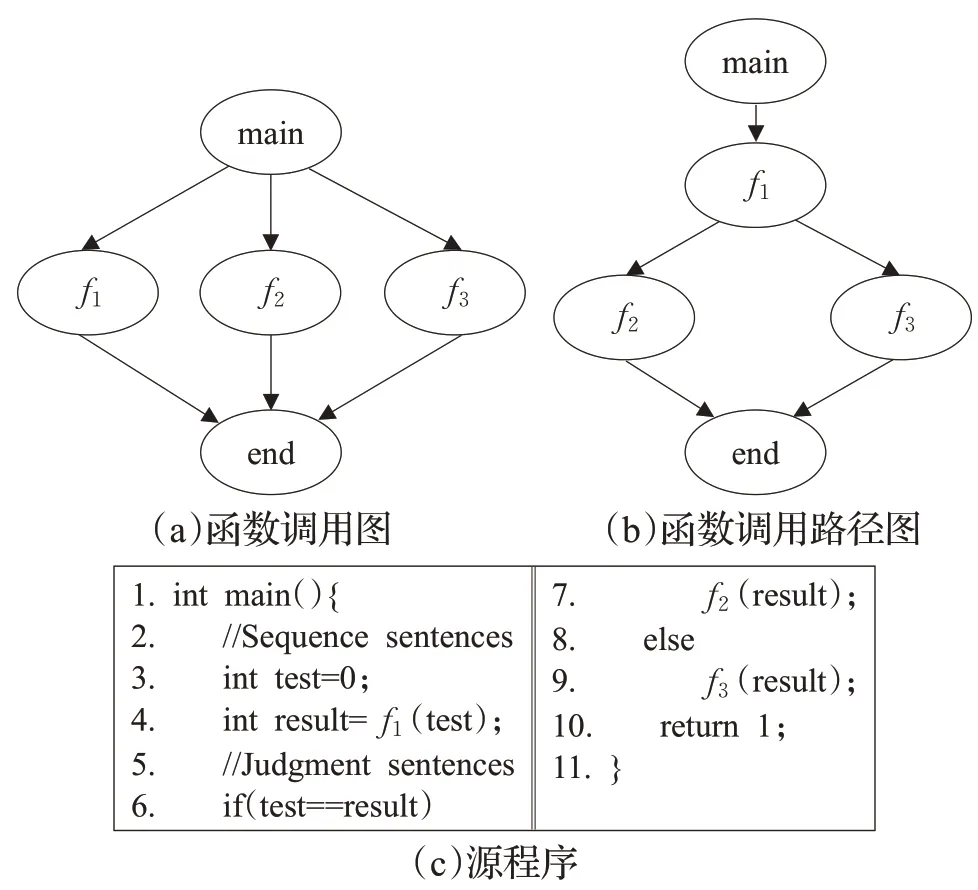
圖1 函數調用圖與函數調用路徑圖對比

遺傳算法的核心部分包括：（1）確定種群染色體編碼；（2）生成初始種群；（3）構建適應度函數以及評估個體適應度；（4）利用遺傳操作算子實現進化。其中，常用的編碼方法有二進制編碼、實數編碼和符號編碼等，遺傳操作算子包括選擇算子（select operator）、交叉算子（crossover operator）以及變異算子（mutation operator）[19-20]。

在預處理階段，遺傳算法根據實際問題的參數進行編碼，組成染色體；其次，初始化一定規模的種群，由多個個體組成；然后，算法通過適應度函數衡量每個個體的優劣，采取選擇、交叉、變異等遺傳操作算子對種群進行演化搜索，直到滿足終止條件；最后，輸出得到的最優解。遺傳算法的執行過程如圖2所示。

3 錯誤定位方法FGAFL

3.1 方法框架

圖2 遺傳算法執行過程

本文針對多錯誤定位問題提出FGAFL 框架，將軟件錯誤定位的研究粒度提升到函數級別，同時提出新的適應度函數，將基于函數調用路徑得到的函數之間的關聯度作為適應度函數的懲罰因子。FGAFL框架的主要研究內容包括三部分：一是對待測程序以及測試用例進行預處理；二是利用遺傳算法搜索尋找最優候選種群；三是根據得到的最優解確定有錯誤的函數。

在預處理階段，運行測試用例得到每個測試用例對函數的覆蓋信息和運行結果，構建覆蓋矩陣和結果向量，同時分析靜態待測程序的函數調用路徑，量化函數之間的關聯關系；在遺傳算法搜索階段，采用二進制編碼方式對問題進行參數編碼，構建初始種群，使用選擇、交叉和變異三種算子對種群進行操作，不斷進行迭代演化，直到終止條件被滿足，得到最優候選種群；在錯誤定位階段，統計并分析得到的最優候選種群，對應到程序中具體的函數，得到最終的函數可疑度排序。

圖3為FGAFL框架的整體流程。

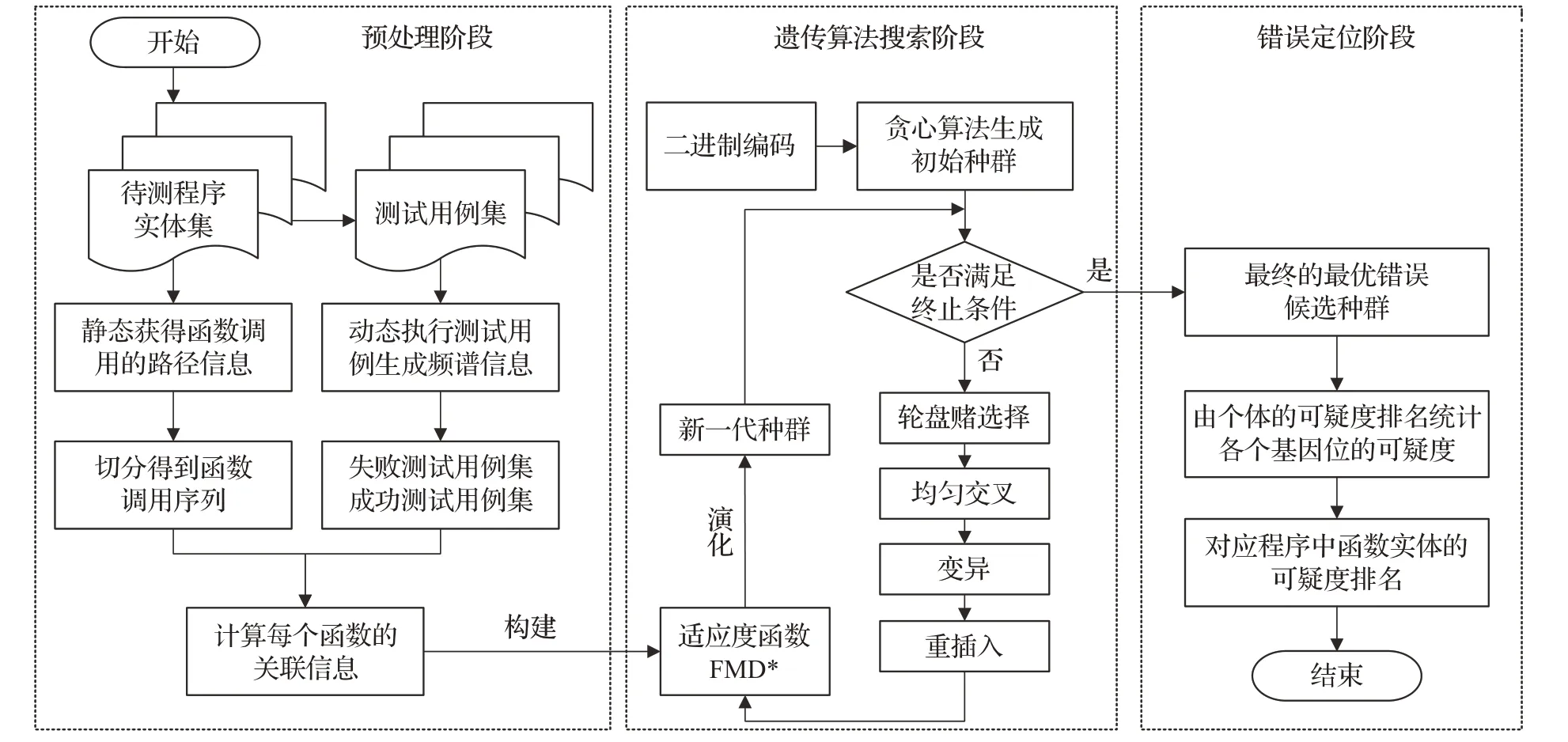
圖3 整體流程圖

3.2 預處理過程

3.2.1 染色體編碼方式

本文采用二進制編碼方式，將個體C 表示為一個二進制向量C={c1,c2,…,cn}。其中n 為被測程序中可執行函數的個數，ci表示第i 個函數是否存在錯誤。若ci=0，則該被測程序中第i 個函數被認為不存在錯誤；若ci=1，則該被測程序中第i 個函數被認為存在錯誤。

例如，有個體C={0,1,0,0,0,0,1,0,0,0}，表示被測程序中有10個可執行函數，其中第2個函數和第7個函數被認為存在錯誤，其余函數不存在錯誤。

3.2.2 函數關聯度計算

計算函數之間的關聯度有以下兩個步驟：首先，分析程序中的數據流和控制流的邏輯關系，得到函數調用路徑圖；其次，結合函數調用路徑圖和覆蓋矩陣、結果向量，分析并量化各函數間的關聯關系。

本文選擇Gini 指數作為量化函數調用序列中目標函數與運行結果之間聯系的指標。一般來說，Gini指數用于衡量數據的不純度或者不確定性，Gini 指數越大，表示數據集的純度越小。舉例說明(f1調用函數f2、f3)，如表1所示。

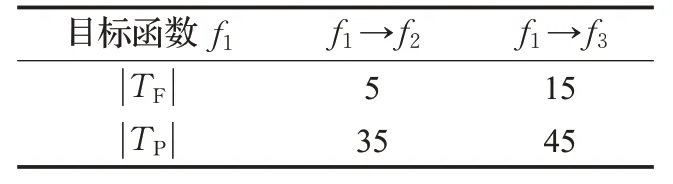
表1 函數調用的關聯關系示例

表1中，第二行第二列表示覆蓋該調用序列f1→f2的失敗測試用例的個數為5，第三行第二列表示覆蓋該序列的成功測試用例的個數為35。計算Gini指數如下：

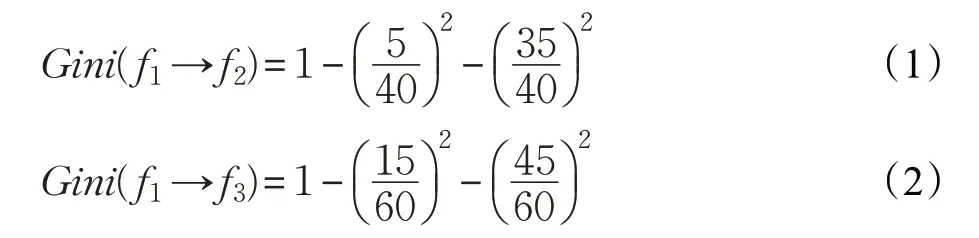
定義函數f1基于函數調用的關聯關系量化后的特征值為relation(f1)，可以得到：

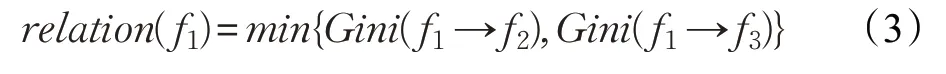
3.2.3 適應度函數

在基于程序頻譜的軟件錯誤定位中，Tarantula、Ochiai以及DStar等可疑度公式主要針對程序中含有一個錯誤的情況。文獻[21]在Ochiai 公式的基礎上，提出了Multi-Ochiai公式作為遺傳算法中的適應度函數。本文在此基礎上提出FMD*可疑度公式，表示為：

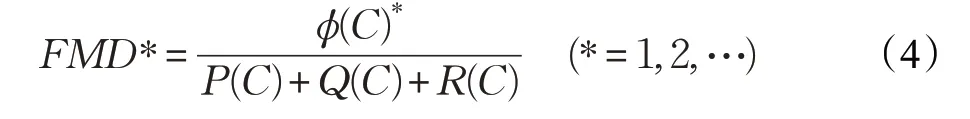
φ(C)是個體C 解釋失敗測試用例的能力，即若一個失敗測試用例經過了個體C 中被認為有錯的函數，則說該個體可以解釋這一失敗測試用例。個體C 能解釋的失敗測試用例越多，則該個體越可疑。φ(C)可以表示為[14]：

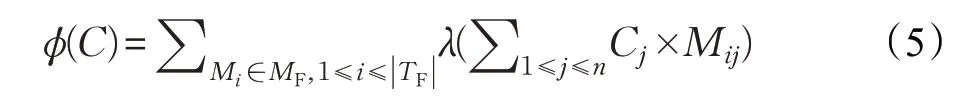
在該公式中，函數λ(x)為示性函數：

類似于φ(C)，P(C)表示的是個體C 解釋成功測試用例的能力。若某個函數被越多的成功測試用例運行覆蓋，則該函數有錯的可能性越小，即個體C 的可疑度與該個體能解釋的成功測試用例的數量成反比。P(C)可以表示為：

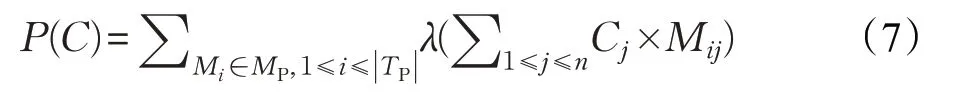
Q(C)表示個體C 中被認為有錯的函數未被失敗測試用例覆蓋的情況。如果一個函數沒有被失敗測試用例運行覆蓋，那么該函數有錯的可能性較低。Q(C)表示為：

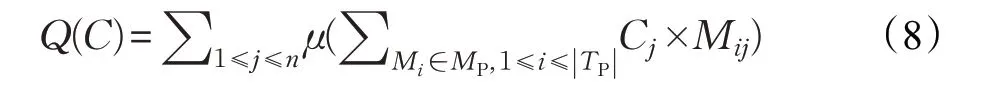
其中，μ(x)為另一個示性函數：

該函數的含義為個體C 中被認為有錯的個體只要未被所有的失敗測試用例運行覆蓋，就將μ(x)的值置為1。

影響因子R(C)表示了函數之間的調用關系，即為上一節中得到的對函數調用之間的關聯關系的量化。R(C)表示為：

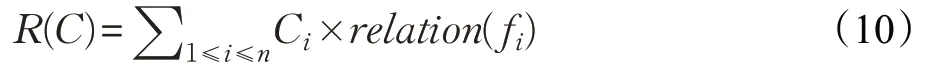
該公式表示對個體C 中被認為有錯的函數計算函數調用關聯關系的特征值，并求和。

3.3 遺傳算法獲得最優種群

3.3.1 初始化種群

高質量和多樣性的初始種群能夠提高遺傳算法的收斂速度以及最終結果的質量，本文結合貪心算法Additional-Greedy（AG）[22]生成初始種群。生成初始種群P 的算法流程如下所示。

該方法的輸入包括失敗測試用例覆蓋矩陣MF以及種群的規模NP。對于有n 個函數的程序首先生成n個個體，同時每個個體只有一個函數被認為有錯，且被認為有錯的函數位置不相同（即生成n 階單位矩陣），如圖4所示：

圖4 生成n 個個體

利用失敗測試用例覆蓋矩陣MF以及圖4 中生成的n 個個體，計算每個個體C 解釋失敗測試用例的能力。如果φ(C)=| TF|，說明個體C 可以解釋所有的失敗測試用例。如果φ(C)＜| TF|，則需要對個體C 表示的函數錯誤分布情況進行修正。利用AG 算法修改個體C的錯誤分布情況，將C 中一個或多個為0的基因位變為1，增加個體中被認為有錯的函數個數，使修正后的個體能夠解釋所有失敗測試用例。對個體進行修正時，需要滿足以下幾個條件：（1）優先選擇能夠盡可能多地解釋失敗測試用例的函數，將其位置變為1；（2）盡可能地選擇還未被認為有錯的函數進行修改；（3）保證修改的函數個數盡可能地少。具體算法過程是：對于一個不能解釋全部測試用例的個體C 來說，選擇能夠解釋最多失敗測試用例的函數fx加入到個體C 中；將fx對應的位置置為1 后，若個體C 能夠解釋所有失敗測試用例，則過程結束，若不能，則需要再選擇其他解釋失敗測試用例能力強的函數加入個體C ，直到該個體能夠解釋所有的失敗測試用例。

獲得一個有n 個個體的種群后，需要對種群的規模進行調整。若n ＜NP，則隨機復制NP-n 個個體補充到初始種群中，使種群的規模達到預定的NP；若n ＞NP，則選擇適應度值較高的NP個個體組成初始種群。

該初始種群生成算法只需挨個檢查圖4 中的n 個個體，判斷解釋失敗測試用例的能力即可。該算法在最壞情況下是n 個個體均不能解釋全部失敗測試用例，需要對所有個體進行修正，時間復雜度為T(n)=O(n2)；最好情況是均可以解釋全部失敗測試用例，不需要對其修正，時間復雜度為T(n)=O(n)。因此，該初始種群生成算法的時間復雜度為T(n)=O(n2)。

通過AG過程構建初始種群：一是保證初始種群中的每個個體C 都能夠解釋所有失敗測試，具有較高的適應度；二是使個體C 中被認為有錯的函數的數量盡可能少；三是使不同個體之間有不同的錯誤分布情況，保證初始種群的多樣性。

3.3.2 遺傳算子

得到初始種群之后，需要利用遺傳操作算子迭代優化，產生優質的個體組成新種群，主要包括選擇、交叉和變異三種遺傳算子。

（1）選擇算子

選擇算子（Selection Operator）模擬了自然界的自然選擇。適應度高的個體能夠以較大的概率被選擇，直接遺傳到下一代或者進行后續的交叉、變異操作。

本文將輪盤賭選擇策略作為選擇算子，基本思想是個體被選擇的概率與其適應度函數的值成正比。假設種群大小為n，個體i 的適應度為Fi，則i 被選中遺傳到下一代種群的概率為：

1771年10月間，葉卡德琳娜二世頒布了“關于廢除土爾扈特汗國的命令，同時取消了‘汗’和汗國總督的稱號”。(參見《卡爾梅克蘇維埃社會主義自治共和國史綱》)由于這項命令的實施，建立于伏爾加河流域一個半世紀的土爾扈特汗國已不復存在；

（2）交叉算子

交叉算子（Crossover Operator）通過交換兩個個體部分位置的信息，組合出新的個體遺傳到下一代種群。本文采用均勻交叉（Uniform Crossover）策略，使兩個父代個體的每對等位基因點都能夠以一定的概率Pcro進行交換。

舉例說明，選擇兩個個體被作為父代個體進行交叉：

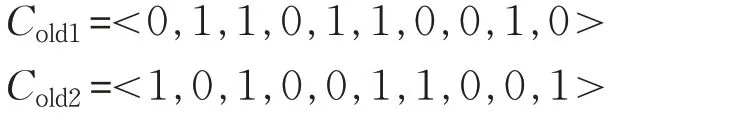
隨機生成一組屏蔽字Mask，與個體長度等長。對于其中的每一位mi，若mi=1，則父代個體對應的基因位進行交換，遺傳到子代個體；若mi=0，則子代個體分別繼承對應的父代個體的基因值。以如下屏蔽字為例：

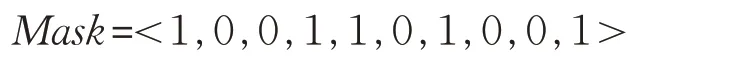
最后，經過均勻交叉后得到子代的兩個個體為：

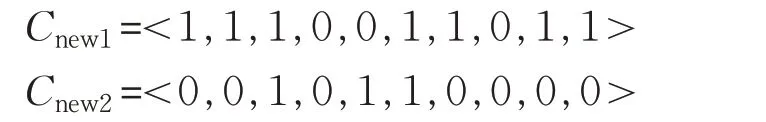
（3）變異算子

變異算子（Mutation Operator）是產生新個體的輔助方法，是指將個體中某些編碼位上的基因值，用該編碼位置的其他等位基因來替換。一般來說，變異概率Pmut的建議取值范圍為0.000 1～0.5。

針對本文的問題，選擇較低的變異概率Pmut進行變異。同時，為了避免個體中的基因從0無限制地變異為1，設置參數para 控制個體中1的數量。當個體中錯誤的數量超過para 時，個體中的基因不再從0變異為1，使得個體不再通過變異產生更多的錯誤位置。

3.3.3 重插入與終止條件

在本方法中，設置迭代次數Ngen作為終止條件。在得到初始種群之后，迭代進行遺傳算子運算以及重插入操作，直到循環的次數達到Ngen，迭代得到最終的最優候選種群，進行下一步確定軟件錯誤位置的操作。

3.4 確定錯誤位置

經過一系列遺傳操作算子的計算操作得到最優候選種群之后，需要將得到的錯誤分布種群轉換為對應的函數可疑度的排名。若個體的適應度值較高，說明該個體代表的程序錯誤分布較為可疑。首先，比較最優候選錯誤種群中每個個體的可疑度，按從高到低的順序進行排列。然后，根據得到的有序排列的種群，統計所對應的函數的可疑度情況。適應度值排名越靠前的個體中，同一位置的函數被認為含有錯誤的次數越多，則該函數實際有錯誤的可能性就越大。以如下最優候選錯誤分布種群為例：

上述種群中按個體的適應度由高到低、從上往下排列，排序越靠前的個體中被認為有錯的函數的可疑度越大。在第一個個體中編號為2、6、9的函數被認為有錯，同時參考種群中其他個體的分布情況，若分布情況相同，則隨機排序。該例中，編號為6的函數在前3個個體中均被認為有錯，該函數的可疑度最高，其次為編號為2的函數。因此，通過該種群最終得到的函數可疑度排序為＜e6,e2,e9,e1,e4,e3,e7,e5,e10,e8＞。

4 實驗評測

為證明FGAFL 方法的有效性，分別針對單錯誤和多錯誤情況設計實驗。

4.1 實驗數據與評測指標

4.1.1 實驗數據

本文選取來自SIR（http：//sir.unl.edu/portal/index.php）網站的測試程序Siemens Suite作為實驗數據。Siemens Suite被視為評估錯誤定位技術有效性的典型數據[23]，包含7個C語言程序，代碼行數最多有565行，可執行代碼行數最多有203行，屬于小規模程序，分別是printtokens、printtokens2、replace、schedule、schedule2、tcas、totinfo。該測試套件中的每個程序都包含一個正確版本和多個錯誤版本，且大多數的錯誤版本中只有一個錯誤，因此選擇在printtokens、replace、schedule 和tcas 程序中植入多個錯誤，用于多錯誤定位效果的驗證。本文實驗評測程序的主要信息如表2所示。

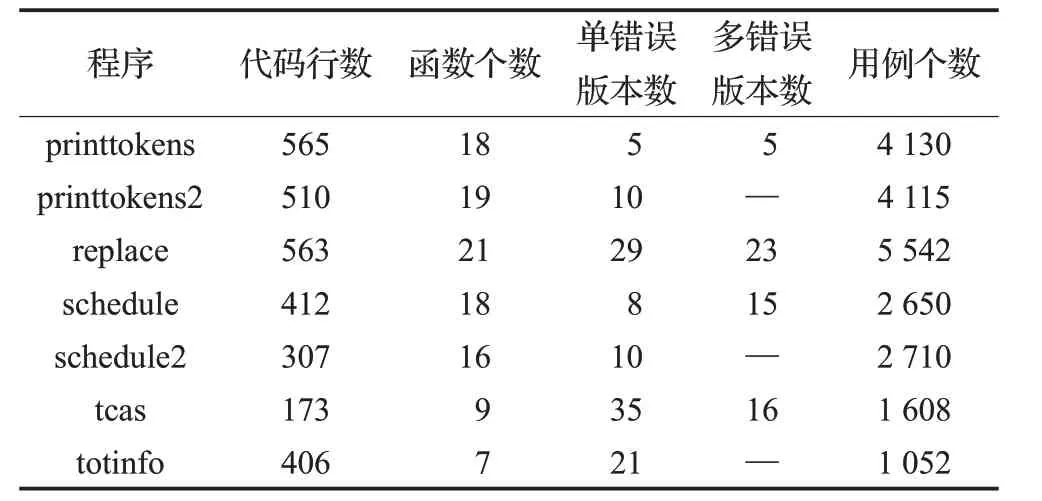
表2 Siemens Suite程序的主要信息

4.1.2 評測指標

本文在Abreu 等人[4]提出的評測標準的基礎上將EXAM 作為評測指標，定義為發現程序中所有錯誤時需檢查的代碼行數占總程序中代碼行數的百分比，具體公式為：

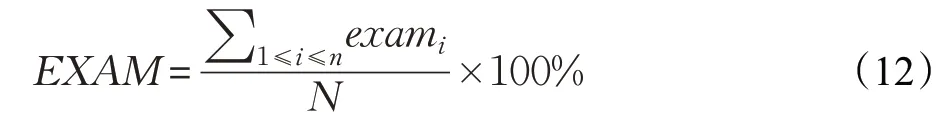
其中，exami表示檢測到第i 個錯誤需要檢查的代碼行數，n 表示程序中錯誤總個數，N 表示程序中總代碼行數。該評測指標適用于單錯誤定位和多錯誤定位，當EXAM用于評價單錯誤定位問題時，可以表示為EXAM=exam/N×100%，即為發現程序中錯誤需要檢查的代碼行數占總代碼行數的百分比。

4.2 實驗內容與結果

本文實驗內容主要分為兩方面：一是驗證在適應度函數FMD*的指數（*）不同取值的情況下，FGAFL 方法的定位效果；二是將FGAFL方法與經典方法進行對比。

4.2.1 不同指數（＊）的影響

在本節中，針對適應度函數FMD*不同的指數（*）進行實驗，*的取值范圍為1～30，增量為1，實驗結果如圖5所示。

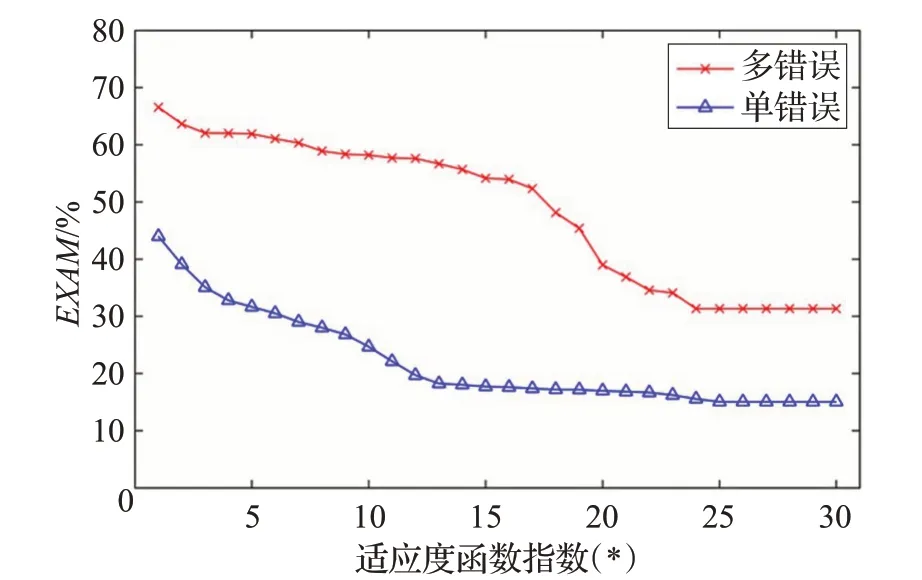
圖5 FGAFL在不同指數（*）數值下的錯誤定位效果

從圖5 中可以觀察到，隨著指數（*）值逐漸增大，EXAM 值逐漸減小并最終趨于穩定，即找到程序中的錯誤需檢查的代碼量隨著指數（*）的增大而減少。同時，在單錯誤定位情況下的EXAM 比多錯誤定位情況下更早地趨于穩定。由此可以認為，前期指數（*）增大對單錯誤定位效果影響較大，可以較快地提高定位效果，而對于多錯誤定位則需要指數（*）增大到一定程度才會較為明顯地提高定位效果。多錯誤定位與單錯誤定位不同的是，一般程序中的多個錯誤會跨越多條語句或多個函數，需依次檢查排名較為靠前的函數，在確定第一個錯誤的位置后仍需檢查后面的函數，直到發現所有的錯誤為止。而這些被檢查的函數中可能沒有錯誤但依然被較多的失敗測試用例經過或較少的失敗測試用例未經過，因此需要賦予φ(C)更多的權值才能較為明顯地提高定位準確性。

4.2.2 與其他方法的對比實驗

針對單錯誤和多錯誤程序進行實驗，選取經典的錯誤定位方法Ochiai、Tarantula 和DStar2 進行對比。這三種方法均是通過構造可疑度公式，分析程序運行時的覆蓋情況和運行結果，得到程序中每一個實體有錯誤的可能性（即可疑度）。

實驗設置適應度函數FMD*的指數（*）為2 和10，表示為FMD2、FMD10。實驗結果如圖6所示。

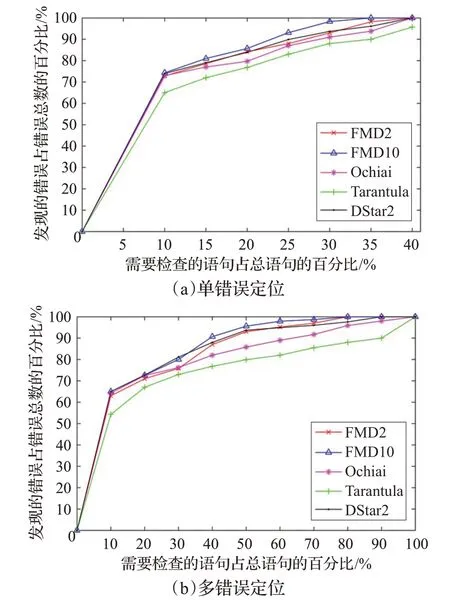
圖6 對比實驗結果

從圖6中可以看出，無論是單錯誤定位還是多錯誤定位，FGAFL（圖中表示為FMD2、FMD10）、Ochiai 和DStar2 方法均明顯優于Tarantula。圖6（a）是針對單錯誤定位得到的實驗結果，FGAFL 的整體定位趨勢與其他方法類似，且在檢查程序中的語句為30%時，FMD10能檢查出的錯誤數更接近于100%，FMD2 的定位效果要略差于FMD10。針對多錯誤定位得到的實驗結果為圖6（b），可以看出FGAFL、DStar2 方法要明顯優于Ochiai 和Tarantula 方法，FMD2 與DStar2 的定位效果類似，但是FMD2要早于DStar2檢查到全部錯誤。從檢查的語句為40%開始，FMD10 的定位效果都要優于其他方法。

另外，統計了FGAFL 方法與Ochiai、Tarantula 和DStar2方法在各程序版本上的平均執行時間，經多次實驗取得平均值。這四種方法均需要執行測試用例收集程序頻譜信息，因此只需關注錯誤定位部分的執行效率，如表3所示。其中Ochiai、Tarantula和DStar2方法只需計算程序中各個語句的可疑度即可，執行時間較短，然而這三種方法在多錯誤定位中效果不佳，且理論上應多次運行逐個定位。雖然執行時間短，但需要花費較多的人工時間去確定錯誤的位置。本文提出的FGAFL方法需要通過遺傳算法迭代尋優，但是需要檢查的代碼量比較少，提高了人工檢查錯誤的效率。

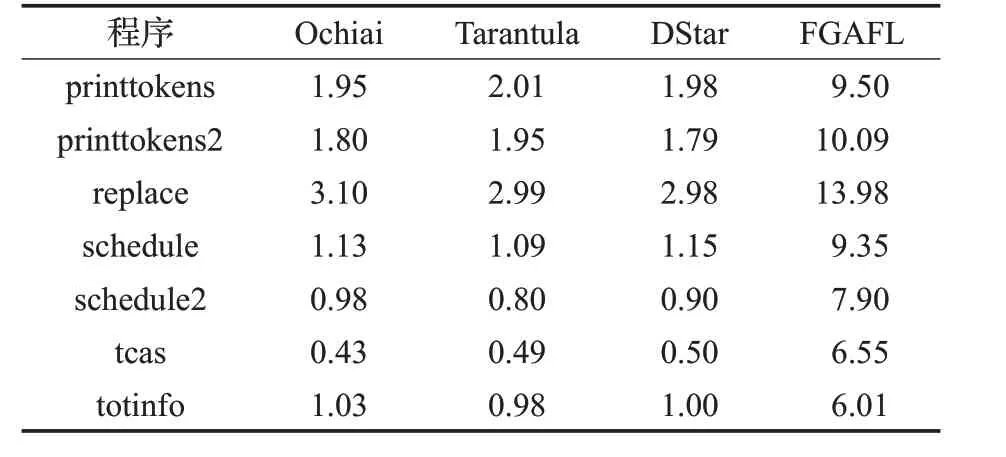
表3 執行時間比較 s

5 結束語

本文基于函數調用路徑的知識，在遺傳算法的基礎上提出了一種函數級別的軟件錯誤定位方法，主要包括以下研究內容：

（1）將軟件錯誤定位問題轉化為一類組合優化問題，利用改進的遺傳算法搜索求解，結合錯誤定位的特點對生成初始種群的方法進行優化。

（2）結合函數調用路徑技術，在已有的適應度函數上進行改進，提出新的適應度函數FMD*，保證在搜索尋優過程中可以有效地衡量個體優劣。

（3）將函數作為錯誤定位的研究粒度，可以有效地縮短個體的長度，降低搜索空間的規模，提高搜索效率。

（4）選取Siemens Suite 作為實驗數據，設計評測指標并進行實驗，同時選擇經典的錯誤定位方法進行定位效果的對比。實驗結果表明，本文提出的方法FGAFL具有可行性和有效性，且有較高的精度和效率。

除此之外，在本文方法的基礎上仍有一些值得關注的問題需要進行后續的研究：

（1）嘗試將本文方法應用到更大型的程序中進行實驗，包括Linux 系統下運行的程序以及不同語言的程序。

（2）為了進一步提高本文方法的性能，嘗試將遺傳算法與其他搜索算法結合，或者選擇不同的搜索算法進行實驗。

（3）進一步考慮將函數粒度的研究與語句粒度相結合，做到先定位到函數后定位到語句，對函數中的語句進行可疑度排序，進一步提高定位錯誤的效率。