“五步問題學講方式”讓課堂翩翩起舞
——以“向量的數(shù)量積”為例

引言：“五步問題”就是問題預設、問題檢測、問題生成與探究、問題鞏固、問題預留；預設就是讓學生會用數(shù)學眼光去觀察世界，感悟知識的來源；檢測、生成、探究就是讓學生會用數(shù)學思維思考世界，領會知識的思維；鞏固、預留就是讓學生會用數(shù)學語言表達世界，真正做到知識“學進去”，“講出來”。筆者以執(zhí)教蘇教版數(shù)學必修四“向量數(shù)量積”第一課時教學實錄為例，談談自己的做法與思考。

一、課堂實錄

1.問題預設

問題1 向量的加法、減法、數(shù)乘如何定義? 加法、減法滿足什么法則? 它們的運算結果是什么?

生(齊聲回答)：向量的加法滿足平行四邊形法則和三角形法則；減法滿足三角形法則；它們的運算結果是一個向量。

師：很好! 下面我們來看一張圖片。

生：好漂亮!

學生的興趣上來了，眉飛色舞和同學交流。

師：這是哪個學院的建筑?

生：搖頭。

師：英國劍橋大學——國王學院。

生1：(聲音洪亮)蘋果樹! 牛頓定律!

師：對! 這位同學很聰明! 我們可不可以向偉大科學家牛頓一樣他坐在蘋果樹下思考出牛頓定律；向量可不以可以像實數(shù)一樣進行“相乘”? 來看下問題2。

意圖 通過類比實數(shù)運算讓學生知道向量可以進行“相乘”，這就是用數(shù)學的眼光觀察世界。另一方面用名人故事的引入，激發(fā)學生的好奇心，增強課堂活躍氣氛，促進學好的數(shù)學動力和信心。

問題2 向量加法以物理中的“位移”為背景，對于向量相乘，可以用物理中的哪個作為背景模型?

生(有的小聲)：功。

師：對，我們一起來研究。

問題2.1 一個物體A在水平力F的作用下運動了位移S，力F做的功為多少?

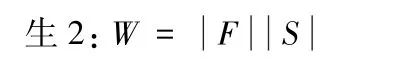
問題2.2 有一個豎直向上的力F1，但沒有提起物體，那么力F1做的功為多少? 為什么?

生3：做功為0，因為力F1在豎直方向沒有位移。

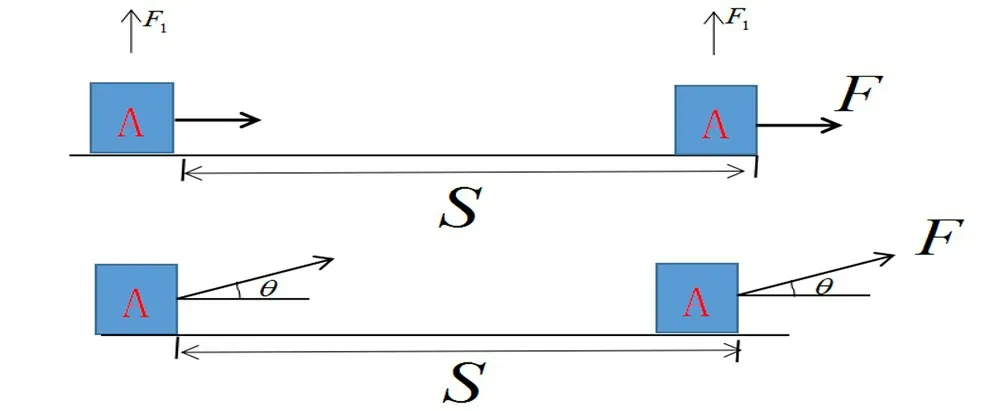
問題2.3 一個物體A在力F的作用下產(chǎn)生位移S，且F與S的夾角為θ，那么力F所做的功為多少?

師：分析到位，物理功底深厚。也就是說功與位移和位移方向上力的大小有關。

問題3 如何從向量的角度來理解功的運算?

師生合作：把力F和位移S看成兩個向量，力與位移得到功就是兩個向量的模與它們夾角的余弦值的乘積。不失一般性，用a→和b→表示兩個平面向量，抽象出來的運算該如何表示呢?

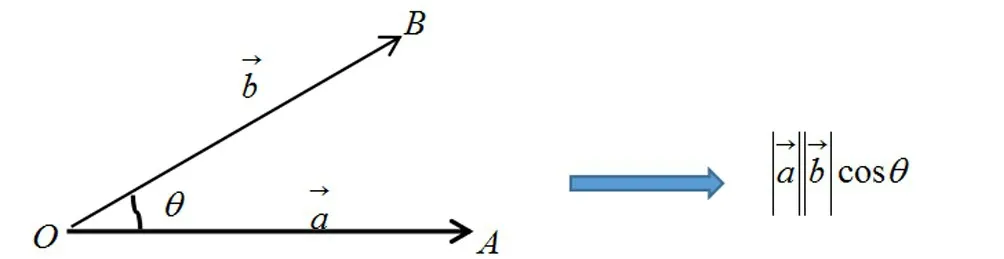
意圖 類比、建模、抽象是數(shù)學基本思想方法。在其指引下，類比力做功模型，抽象到向量的數(shù)量積，從而調(diào)動學生的已有知識向未知知識過度引領，體會到數(shù)量積的實際背景，經(jīng)歷概念形成的過程，領悟到數(shù)學概念的本質(zhì)。

問題3.1 能否由數(shù)量積的定義求出?

生5：由于零向量的方向任意與a→的夾角無法確定不能用公式求解，可以考慮在“功”的實際意義中無論位移還是力有一個為零其結果都為零，所以定義零向量與任意向量的數(shù)量積為零。

問題3.2 如圖兩個向量，它們的夾角怎么作? 夾角范圍為多少?

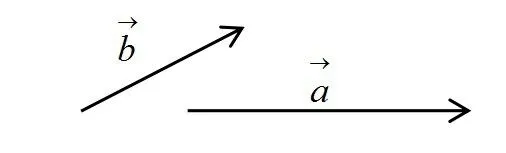
生：看課本，與同學交流總結如下。

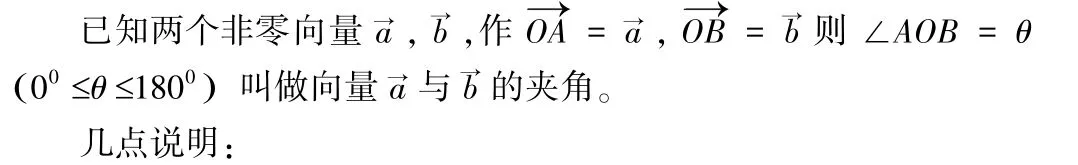
(1)兩個非零向量的夾角，應保證兩個向量共起點，否則平移使之共起點。

意圖 數(shù)學概念學習時必須把內(nèi)容中的關鍵語句理解透，因此教學時要精心設計問題，加強概念的剖析，讓學生在問題分析中學會發(fā)現(xiàn)、提問、解決能力，這就是“自學”。

2.問題檢測

(1)判斷下列說法是否正確。

師：掌聲響起! 不錯，對于向量的平行夾角應該為0°或180°。

意圖 通過兩道基礎題查看學生在課堂上學習的成效。成果的交流就是思維展示的過程，通過生生互助解決學習中問題，獲得成就感，這就是“互學”。

3.問題生成與探究

問題4 向量的數(shù)量積的結果與夾角之間的關系如何?

生10 和生11(合作完成)：從夾角的大小分析。

生12 和生13(合作完成)：從數(shù)量積的數(shù)值角度分析。

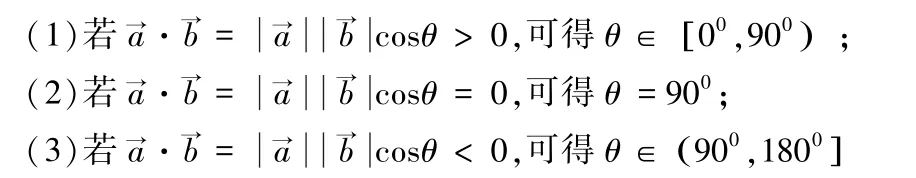
意圖 通過對問題適當?shù)纳桑鰪妼W生對數(shù)量積認知的深度和寬度；經(jīng)過小組合作交流、探究，強化對向量數(shù)量積的理解和掌握，這就是“問學”。

問題5 數(shù)的運算離不開運算律，結合課本去理解和掌握向量的數(shù)量積的運算率。

生：(小組合作、探究、驗證)得出如下結論：

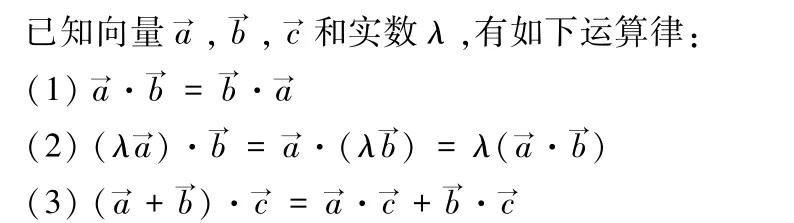
意圖 一方面類比實數(shù)運算律，猜想出數(shù)量積的運算律；另一方面結合已有的知識，通過合作交流證明猜想，培養(yǎng)學生邏輯推理能力。

4.問題鞏固

意圖 強化運算律的理解，培養(yǎng)解決問題的能力，深化和鞏固學習成果；能夠在課堂上正確表達解題思路，讓大家都明白，這就是“教學”。

5.問題預留

在邊長為2 的正六邊形ABCDEF中，

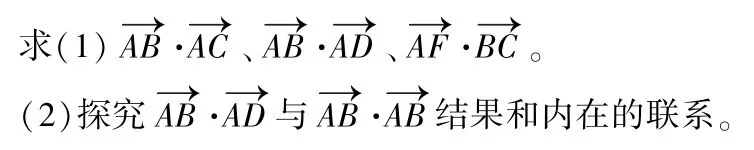
意圖 通過第一問的解題，加強學生對向量夾角的理解，進一步掌握數(shù)量積的定義；對第二問的探究在數(shù)量積定義下對數(shù)量積幾何意義的引入埋下伏筆，這就是“悟?qū)W”。

二、教學反思

課堂應該是以“真學習”為目的。首先，教師在課堂中不應該去追求“教學多樣技術”，而是保障每個學生的“學習權”，實現(xiàn)每個學生真正的學習與成長。其次在課堂教學活動中要積極引導學生以“問題”進行的“五學”行為，讓學生在問題引領下學會類比、歸納、數(shù)學建模、邏輯推理。最后應關注核心素養(yǎng)與知識的內(nèi)在聯(lián)系，以一定的數(shù)學文化和知識為依托，遵循數(shù)學知識的發(fā)展規(guī)律和學生認知規(guī)律，把知識來龍去脈充分展現(xiàn)在學生面前，激發(fā)學生想學習、學好習的動力，從而提高學習數(shù)學的能力，進一步提升學生的核心素養(yǎng)能力。