優化小學數學作業的設計原則探究

龔祖華

（重慶市開州區教師進修學校）

作業是數學教學中的一個重要環節，它不僅能檢測教學效果，還能對學生的學習起到導向的作用。長期以來，由于受應試教育等諸多因素的影響，學生的很多學習活動服從于教師，作業也是如此。對于“做什么”“怎么做”，很多學生沒有發言權，只能執行。這種現象嚴重阻礙了學生創新精神和實踐能力的培養。為了更好地落實新課程理念，有效提升學生的數學素養，我們需要堅持以下原則進行作業優化設計。

一、作業設計要有針對性

針對性是作業設計的首要原則。所謂針對性，就是作業的設計要從教學目標出發，要有的放矢，要緊扣教學內容，要突出重點、難點，也要涉及課后練習的題型，以確保學生對新知的充分理解。圍繞重點、難點設計作業，才能練到點子上，練出成效來。

如小數乘法的實質是整數乘法法則的延伸，為了讓學生盡快掌握如何確定積的小數點位置的方法，可設計如下作業：

小英的計算器壞了，顯示屏上顯示不出小數點，你能很快地幫她寫出下面各式的結果嗎？

已知：328×15=4920。

那么，3.28×15=（ ），328×1.5=（ ），0.328×15=（ ），32.8×1.5=（ ），3.28×0.15=（ ），0.328×0.15=（ ）。

這六道小數乘法題的計算方法是相同的，僅是積的小數點位置不同。他們都是先按照整數乘法“328×15”算出積，再根據小數乘法中因數與積的小數位數之間的關系，在積“4920”中確定小數點的位置。確定小數點的位置時，一定要數清兩個因數一共有幾位小數，再從積的右邊起數出幾位，點上小數點。本題既考查了學生對小數乘法計算方法的掌握情況，又讓學生感受了到小數乘法與整數乘法之間的內在聯系。

同樣，在學習“圓的認識”后，為了讓學生掌握圓的半徑與直徑之間的關系，可設計如下作業：

根據已知條件，你能看出哪些間接條件？（如圖1，單位：cm）

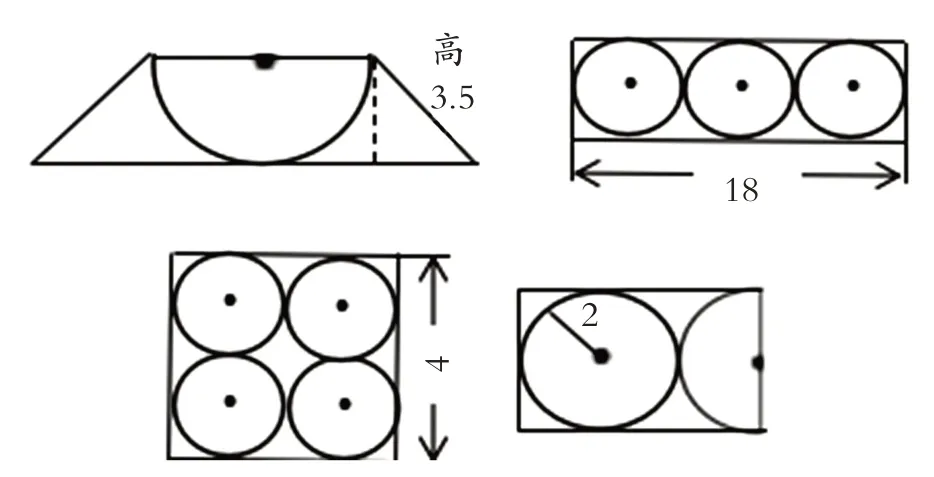
圖1

這四道題，都有進一步掌握和理解圓的直徑與半徑的目的，但又都不是在單一的環境中讓學生去識別和練習，而是把新學知識與舊知識混在了一起，把直徑、半徑放在了一個比較復雜的環境之中，這樣背景就不再那么簡單。訓練學生在排除干擾的同時提高尋找間接條件的能力，這既是為后續學習組合圖形打基礎，更是為培養學生的創造力打基礎。這四道題，已不易直接看出一些間接條件了，需要有“動感”，要靜中看動，才能找到所有的間接條件。學生做到這樣，創造意識已在其中萌發了。

二、作業設計要有趣味性

興趣是最好的老師。學生只有對作業產生濃厚的興趣，才會積極、主動、自覺地完成作業。為了激發學生對作業的興趣，一定要擺脫那種單調乏味的重復練習，要增加趣味性，調動學生學習的積極性，使之產生一種內在的需求感，從而自覺完成作業。

如學習“異分母分數加減法”后，可設計如下作業：

先計算，再想一想怎樣算比較塊？

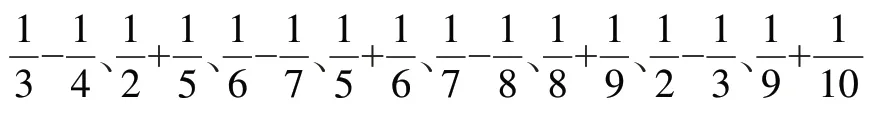
這組題中，分數分母都是互質數，分子都是1。8道題中有7 道是相鄰的兩個自然數，突出相鄰兩個自然數一定是互質數的規律。計算時，只需將分母相乘的積作分母，分母相加（減）的結果作分子，就可算出得數。這樣的作業，計算的數據不復雜，學生計算時感到有趣，同時通過計算能發現一些規律。這樣，能拓展學生的計算技能，進一步完善學生新的認知結構。

在學習“容積和容積單位”后，可設計如下作業：

回家后，挑選一個你最喜歡的土豆，測量出它的體積。

（1）你準備怎樣測量土豆的體積？請設計出操作步驟；

（2）需要準備哪些測量工具？

（3）你能想到幾種測量土豆的方法？

（4）在測量過程中你學到了什么？遇到了什么困難？用到了哪些數學知識？

然后，把測量過程、測量結果和你的感受等寫成一篇數學日記。可以請你的爸爸媽媽利用手機把你測量的過程拍成視頻傳到班級群或分享給其他同學，可以獨立完成，也可以小組合作完成。

這樣的作業，學生既有機會動手操作，又覺得好玩，完成的過程中也會樂此不疲。

三、作業設計要有層次性

《義務教育數學課程標準（2011年版）》指出：“數學課程應致力于實現義務教育階段的培養目標，要面向全體學生，適應學生個性發展的需要，使得人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展。”我們的學生來自于不同的家庭甚至是不同的地域，他們的學習方式、思維方式會有所不同，在學習上就也會表現出差異來。因此，我們設計作業時不能采取一刀切的方式，必須因人而異，因材施教，既關注潛能生和中等生，又要關注學優生。要滿足差異發展的要求，使學生學習的積極性得到保護，個性得到張揚，使不同學生的數學能力都能得到展示。

如學習“圓的面積”后，可設計如下一組題目，讓學生選擇適合的層次做一做（至少選擇一道題目）。

（1）★一個圓的半徑是4 厘米，它的面積是多少平方厘米？

（2）★★一個圓的周長是25.12 厘米，求它的面積。

（3）★★★在一個邊長是8 厘米的正方形內剪下一個最大的圓，求這個圓的面積。

這3 道題都是求圓的面積，但難度系數不一樣。第1 題主要考查學生的基礎知識、基本技能的掌握情況，一般水平的學生都能解決。第2 題沒有給出直接條件，所以難度系數比第1 題有所提升。解答第3 題需要空間想象能力，能想到“正方形內剪一個最大的圓，那么正方形的邊長就是圓的直徑”。因此，這道題要考查的數學知識點是正方形的特征、邊長與它里面最大圓的直徑的關系，以及直徑與半徑的關系。這不是單一地呈現知識，而是將知識融合后考查，培養學生及時捕捉有效數學信息的能力。這三道題的難度系數逐步加深，學生可以根據自己的能力與興趣至少選一道題解答。

設計分層作業之后，潛能生也會動筆，不至于交空白作業或干脆抄襲；中等生也能基本完成作業，達到教師的要求；而學優生更能發揮出他們的個性來，他們能提出一些具有挑戰性的問題。這樣，就能真正實現了“不同的人在數學上得到不同的發展”的教學目標。

四、作業設計要有開放性

《義務教育數學課程標準（2011 年版）》明確提出：“為了考查學生的創造能力，可以設計開放性問題”。在數學教學中，適當設計一些開放性的作業，能使學生有機會運用一系列思考策略進行實踐活動，以鞏固和實踐相關的知識和技能，發展數學思維能力，能使他們由模仿走向創新。有些題目的答案可以不是唯一的，可以留給學生更多的思考空間；有些題目可以不給全條件，由學生去補充；有些題目可以給一組條件和問題，由學生自己組合編題；有些題目可以有多種解法，讓學生比較哪種最簡便。

如學習“相遇問題”后，可設計這樣一道開放題：

一列貨車和一列客車同時從甲、乙兩地相向而行，貨車每小時行50 千米，客車每小時行60 千米，行了3小時后__________。甲、乙兩地相距多少千米？

要求學生補充條件后再解答。學生會發現，貨車和客車行駛3 小時后，運動結果會有三種情況：①行了3小時后相遇；②行了3小時后兩車還相距一段路程；③行了3 小時后兩車相遇后又相距一段路程。不同層次的學生也許會補充不同思維層次的條件。

在學習“長方體和正方體的表面積”后，可設計這樣一道開放題：

用12 個棱長1 厘米的小正方體拼成一個長3 厘米、寬與高都是2 厘米的大長方體（如圖2 所示），再從上層去掉一個小正方體，現在它的表面積是多少平方厘米？

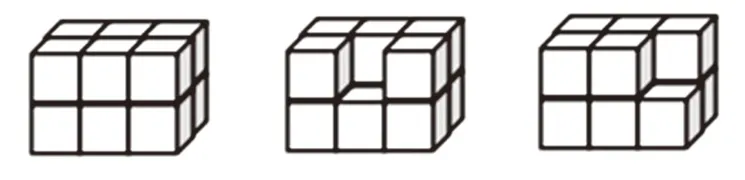
圖2

可以在棱的中間去掉1 個小正方體，表面積比原來增加了2 個小正方形的面積；如果去掉的是頂點上的一個小正方體，與原長方體相比表面積不會發生改變。

五、作業設計要有自主性

《義務教育數學課程標準（2011 年版）》明確提出：“有效的教學活動是學生學與教師教的統一，學生是學習的主體，教師是學習的組織者、引導者與合作者”。要使學生的個性得到張揚，創造能力得到釋放，使“學生是學習的主體”這一理念得到真正落實，教師就必須在“自主”作業上下功夫。讓學生根據自己的喜好和需要選擇作業形式、內容，他們就會對學習產生興趣，就會把作業當作一種享受，一種愉悅的體驗。

如學習“復式統計表”后，可以讓學生記錄自己在一個星期內每天上學途中所需要的時間，并從這些數據中發現有用的信息。這樣的活動有利于培養學生的數據分析意識：知道在現實生活中，有許多問題可以先調查數據，通過對數據的分析得到結論。如果把記錄時間精確到分，可能每天上學途中需要的時間是不一樣的，可以感悟數據的隨機性；更進一步，可以感悟到雖然數據是隨機的，但數據較多時具有某種穩定性，可以從中得到很多信息。此外，還可以讓學生調查本班同學爸爸、媽媽每天工作和做家務的時間，讓學生通過課外實踐活動，再次經歷一個完整的統計過程，增強統計意識和能力。結合統計表中數據的分析，還可以適時滲透感恩父母、熱愛勞動等教育，體現學科的育人價值。

另外，還可以讓學生自選或自編作業。自選作業，就是學生根據自己的實際情況，自己選擇課本上的習題或教師出的題目作為作業；自編作業，就是讓學生根據某節課的內容為教師設計試題，并寫出答案，再同桌或小組內交流。尤其是單元復習或期中期末復習階段，可以以小組合作的形式讓學生根據單元的知識點出一份他們心目中的測試卷，然后交換完成并批改。學生自己出題的過程就是一個積極思考的學習過程，也是自我提高的過程。因為要展現自己的水平，學生會絞盡腦汁地思考，在批改同學的作業時，也會特別認真。事實證明，學生對自己“創造”出的題目會更感興趣，練習也更投入、主動。教師要根據不同內容的特點，尋找一個最佳切入點，既讓學生自己編題，又注重激發其創造性。