一道中考題的賞析與建議
——2019年江蘇省蘇州市中考試題第18題賞析

一、原題呈現

如圖1-1，一塊含有45°角的直角三角板，外框的一條直角邊長為8cm，三角板的外框線和與其平行的內框線之間的距離均為，則圖中陰影部分的面積為_______cm(結果保留根號)。

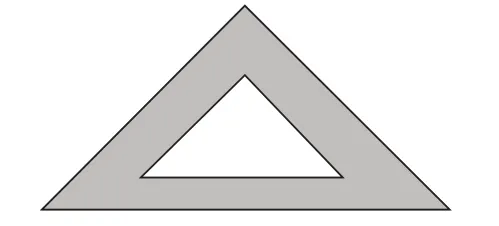
1-1

二、解法分析

這是一個非常簡單的題，其實際問題就是我們平常用的三角板中的一個，學生平時很少去關注，本題考查的知識點不多，給我們感覺題目很直接明了，很快能夠讓我們進入解題的狀態，但是卻讓我們無從下手。解決問題需要我們利用學過的知識點把實際問題轉換為數學問題，這是解決本題的難點。如何建立數學模型要從我們學過的簡單的知識點出發，解決問題的知識點不會發生改變。本題考查兩個簡單的圖形的綜合應用，1.平行線之間的距離；2.等腰直角三角形的性質。考查需要利用簡單的知識點建立數學模型，需要添加不同的輔助線把需要解決的問題凸現出來。

三、解法欣賞

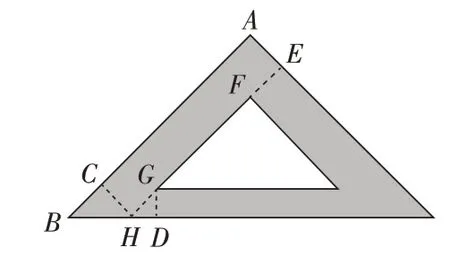
解法一：如圖3-1：過頂點A作AB垂直于大直角三角形底邊

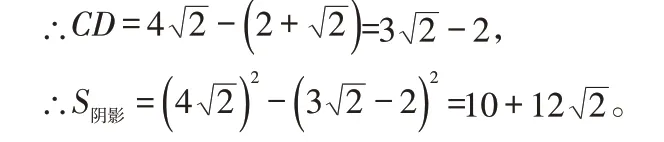
∵含有45°角的直角三角板，

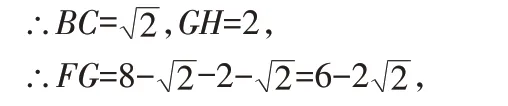
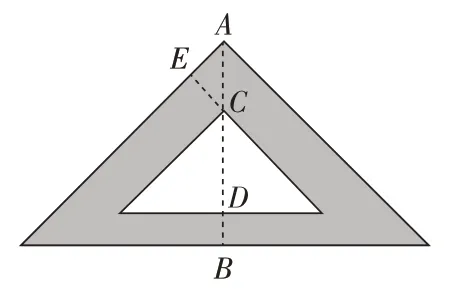
3-1

3-2

3-3

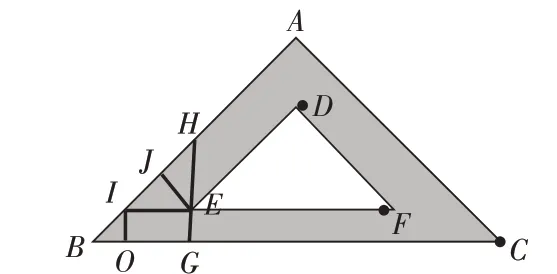
解法三：如圖3-3，AB=AC=8，,過E作GH⊥BC交AB于H點，延長FE交AB于I點，過E作EJ⊥AB于J點，則，

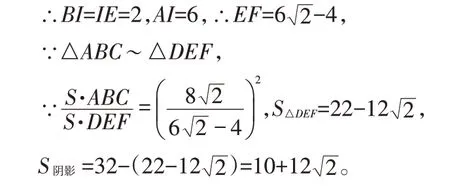
四、試題分析

1.來源于生活，存在于身邊

一把常用的三角板對于所有人來講都是平時常用的作圖工具，但是里面隱藏的數學問題確實很少有學生會去關注，中考題提示我們身邊數學問題無處不在，要關注身邊的數學小問題，嘗試把身邊的現象轉換成數學問題去解決。

2.數學題簡潔而不簡單

從題中我們發現，一個簡單的三角板給出邊長和內外框線之間的距離去解決陰影部分的面積，從題干的條件看沒有一大堆的條件，簡簡單單我們一目了然，能夠很快讀懂題目的條件和所求的問題，也很好地判斷45°角的直角三角板隱含的條件，但是要求解卻不是那么容易，應充分發揮對知識點的應用，建立數學模型等數學能力問題，體現小小的現實問題存在大大的數學世界。

3.方法多樣性，但緊抓知識點

一道中考題的方法沒有受到局限，可以從不同的角度去思考問題，多種方法入手去解決問題，解題的入口很寬，但是不論用什么方法我們發現知識點永遠不會改變，都需要緊扣知識點建立數學模型，對知識點得到充分的應用。

五、感想與建議

1.重視生活中的數學例子

數學來源于生活，在生活中有著大量的數學例子，這些例子應引起我們注意。感受數學中的知識點能夠幫助我們解決生活中的問題，在平時我們也要注意一些數學中的生活題，嘗試去尋找其中的數學知識點。

2.重視一題多解并歸納

一題多解能夠拓寬解題思維，能夠對題的理解更加深刻，但是在課堂中除去多種解法來分析問題的時候，還需要對解法進歸納，對知識點進行羅列，使問題的本質更加清晰化。

3.重視加強對試題的欣賞

學生不是解題的工具，也需要我們用美的眼光去欣賞試題，欣賞數學世界的美感。

4.重視基礎知識的應用

在解中考題中我們發現，僅掌握簡單的知識點很難解決問題，對知識點的死記硬背也解決不了問題，這就需要我們對知識點進行拓展，讓知識點活起來，讓知識點融入到現實問題中去幫我們建立數學橋梁，從而解決問題。