建模思想在中考數學復習中的應用實踐

現如今，建模的利用率越來越高，建模為初中教師的數學教學以及學生的學習帶來了很大的幫助，其不僅是一種解決問題的基本方法，更是學生解決問題時必不可少的根本思想。

一、方程(組)模型

簡單來講，這一模型是應用方程(組)模型，對生活中存在的數量關系進行分析。筆者意在通過一個例題，詳細描述建模思想在方程復習中的應用。

例1：現有一店鋪銷售一種合金，用A、B兩種金屬按一定的質量比混合成合金。已知A、B兩種金屬每千克的價格比是3∶4。實際制造時，A金屬少用了20%，B金屬多用了20%，結果合金的價格與原計劃的價格相同。原來兩種金屬的質量比是多少？

第一步：教師通過提問引導學生分析題意。師：“合金價格如何表示？”生：“A的單價×A的質量+B的單價×B的質量。”師：“要表示合金實際價格和原計劃的價格，我們需要知道什么？”生：“A、B的單價，A、B實際生產和原計劃的質量。”師：“你準備如何設數？”生：“A、B兩種金屬每千克的價格比是3∶4，設A金屬每千克的價格是3，則B金屬每千克的價格是4。”

第二步：學生自我嘗試，學生嘗試設數，發現結果兩邊不成立。師：“我們需要求兩種金屬的質量比，不知道比的情況下，設數就會出現題干中的等量關系不存在，為了避免這個問題，我們可以通過設未知數來避免這個問題，但是利用未知數解題必須先建立方程的模型。”

第三步：建立模型：A金屬的單價×A金屬的質量+B金屬的單價×B金屬的質量=A金屬的單價×A金屬的質量(1-20%)+B金屬的單價×B金屬的質量(1+20%)。

第四步：模型求解：設A金屬的單價為3，B金屬的單價為4；原計劃中A金屬的質量為x，B金屬的質量為y。根據題意得3x+4y=3×(1-20%)x+4×(1+20%)y，3x+4y=2.4x+4.8y，0.6x=0.8y，x∶y=0.8∶0.6=4∶3，答：原來兩種金屬的質量比是4∶3。需要注意的是，在選擇建模思想進行數學問題教學時，應保持難易適中的原則，并且將合理、創新、真實以及有效作為基礎，從學生實際出發，如此才能達到真正的效果。

二、不等式(組)模型

數量間的不等關系在日常生活中較為常見，筆者通過以下例題將建模思想在不等式組中的應用進行詳細說明。

例2：一工廠有50名員工，工廠想要添加幾條生產線，需要在這50 名員工中抽取，在抽取分工后，余下的員工要求每月人均增加40%的產值；而被抽取的員工每月人均產值需要變為以往的3倍，若余下的員工每月生產的總產值不低于分工前總產值，同時抽取的員工每月生產的總產值又不低于分工前每月生產總產值的一半，那么想要滿足這一情況，抽取人數需在什么范圍？

1.教師通過提問引導學生分析題意。師：“同學們，你們從題目中得到了哪些信息？”師：“剛才有好多同學都回答了自己找到的信息，我們也能看出此題涉及的量多，并且未知的量也較多，面對這么多未知數，我們首先應該怎么處理題目呢？”2.學生整理題目數據并建立數學模型。生：“我們需要將題目中的數據和信息進行整理。”經過整理我們可以得到：分工后，留在原生產線上工作的員工每月的總產值是：留在原生產線上的人數×分工前員工每月的人均產值×(1+40%)≥50人×分工前員工每月的人均產值，到新生產線上工作的員工每月的總產值是：新生產線上的人數×新生產線上員工每月的人均產值≥50人×分工前員工每月的人均產值。3.模型求解。設被抽調到新生產線上的有x人，分工前員工每月的人均產值為y元。

利用數學建模思想解決初中數學不等式問題，重在抽象概括、分析量之間的關系。這種解題思想能夠很好地培養學生應用數學解決實際問題的意識和提高學生分析問題的能力。

三、幾何模型

在日常生活中的諸多方面都能涉及到幾何，如圖形設計、結構設計、測量等，筆者將通過以下例題詳細描述如何利用建模思想構建幾何模型。

例3：如圖，在△ABC中，∠ABC=60°，AD、CE分別平分∠BAC、∠ACB，且相交于點O。求證：AC=AE+CD。

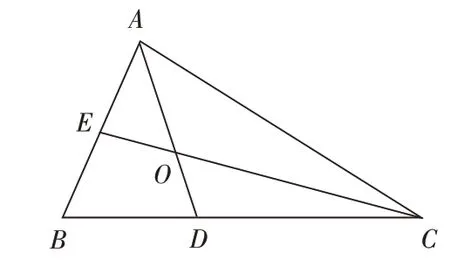
第一步：教師通過提問引導學生分析題意。師：“通過仔細審題，題中只是告訴我們一些與角有關的條件，那么我們應怎樣求線段的和呢？”師：“截長法即在較長線段上截取一段等于兩條較短線段中的一條，再證剩下的一段等于另一條較短線段；所謂補短，即把兩條短線段補成一條線段，再證這條線段與長線段相等。”師：“回憶了這種方法，那么對于這道題目，是采用截長還是補短呢？”

第二步：學生分組討論，提示學生可以參考思維導引。

第三步：建立模型。生1：“利用截長法來做，在AC上截取AF=AE，連接OF，證明CD=CF。”生2：“利用截長法來做，在AC上截取CD=CF，連接OF，證明AF=AE。”

第四步：總結建立構造全等模型的常用方法——添加輔助線。(1)在求線段的和差關系時，會采用“截長補短法”。(2)倍長中線：①已知三角形中線時，常延長加倍中線，構造全等三角形；②有以線段中點為端點的線段時，常延長加倍此線段，構造全等三角形。

倍長中線造“8”字形，出全等有平行。

(3)遇見角平分線經常做輔助線的方法。

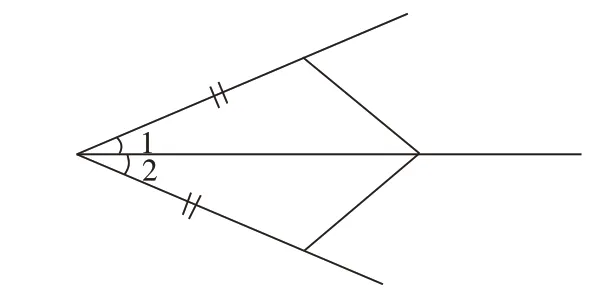
根據對稱的思想，構造全等三角形。

四、函數模型

通過函數能夠展現出事物間存在的關聯，其能夠很好地將現實存在的運動規律及數量關系體現出來。筆者通過以下例題將建模思想在二次函數中的應用進行詳細說明。

例4：藥店一瓶酒精(大瓶)的進價為40 元，經過藥店老板的調查，該酒精一周的銷售量y瓶與銷售單價x(x≥50)元/件，其存在以下關系：銷售單價x(元/瓶)為55、60、70、75；對應一周的銷售量y(瓶)為：450、400、300、250。

(1)T表示一周所得到的銷售利潤，列出T與x兩者間存在的關系式，同時確定銷售單價在哪一范圍內變化時，銷售單價增大銷售利潤也會隨之增大？

(2)武漢新冠肺炎事件得到億萬人民的關注，該藥店決定向武漢寄出商品一周所獲取到的銷售利潤，低于一萬元的酒精貸款下，計算出會有多少的捐款數額？

第一步：建立模型。(1)由銷售量×(售價-進價)=利潤，進而得到函數關系式，最終確定出銷售單價的合理范圍；(2)通過得知酒精貸款在一萬元以下，得出實際進貨量，最終通過計算出最大銷售額。

第二步：進行模型求解。首先，設y=kx+b，由題得：55k+b=450以及60k+b=400，解得：k=-10，b=1000；則y=-10x+1000；由題得S=(x-40)(-10x+1000)=-10(x-70)2+9000，因此可以得到：此函數圖形對稱軸為70，并且開口向下。這表示，當50≤x≤70時，銷售單價增大時，銷售利潤也會增大。其次，通過40(-10x+1000)≤10000 式子得出，在x≥75時，也就是x為75時，利潤為8750元，此時利潤最大。

總之，在初中數學教學環節中，教師應與實際問題相結合，逐漸引導學生通過二次函數知識組建數學模型，從而輕松愉快地解決數學問題。