“另類”求解四力的靜態、動態平衡問題

福建 郭 威

力的平衡作為高中重要的知識模塊，對整個高中學習的重要性不言而喻，本刊第5期發表了在教學實踐過程中摸索出的幾種“另類”求解三力的靜態、動態平衡問題的方法，旨在運用常規方法過程解決繁瑣問題，同樣四力的靜態、動態平衡問題常規解法是正交分解，但有時解決過程非常繁瑣，千篇一律地用正交分解求解四力問題，不僅約束了從物理學視角對客觀事物的本質屬性、內在規律及相互關系的認識方式，而且影響“提出創造性見解的能力與品質”學科素養的落實。為此，本文總結幾種“另類”求解四力的靜態、動態平衡問題的方法，從不同角度思考問題，細細品味卻也蘊含著精妙的物理思維與方法，出奇制勝，僅以此拋磚引玉。

一、四力矢量圖解法

一般情況下求解四力平衡動態問題，常規方法是采用正交分解，列兩式進行化簡求解，在教學實踐中發現該方法解題過程要根據三角函數關系判斷力的變化情況，這樣的解法由于物理量多，解題過程繁瑣，對數學的要求相對要高，常讓學生望而生畏。而作為定性分析四力動態平衡問題，如果采用矢量圖解法，可以非常直觀地看到各力的變化趨勢，從而快速解題。

圖1

( )

A.小球b的機械能守恒

B.懸線OE的拉力先增大后減小

C.懸線OC的拉力先增大后減小

D.小球b受到的庫侖力大小始終為3mg

圖2

【方法點撥】此法關鍵在于四個力構成矢量四邊形的順序，要保證所有力首尾順次連接構成力的矢量四邊形，根據題設要求選定變量與不變量進行動態分析。

【小試牛刀】(原創)如圖3，輕桿P端用光滑鉸鏈固定在豎直墻面上，O端用輕繩吊一重為G的重物，并用另一輕繩斜結在墻N處，在水平向右的拉力F緩緩拉起重物的過程中，繩結位置O不變，則

圖3

( )

A.細繩NO的拉力先變小后變大

B.細繩NO的拉力一直變大

C.細繩對輕桿PO的壓力一直變小

D.細繩對輕桿PO的壓力先變小后變大

【方法演練】對O點以下含重物作為整體為研究對象，受力分析如圖4所示，如果用常規的正交分解，需要設一些已知角并進行解方程組運算，非常麻煩，但四力動態平衡如果用四力矢量圖，解法如圖5，四力構成一個閉合矢量四邊形，就可以直接從這四邊形中動態變化看出BD選項正確。

圖4

圖5

二、摩擦角減力法

【應用示例2】一木箱靜止在水平地面上，木箱質量為m，用水平推力F使物體做勻速直線運動。保持力的大小不變，方向改為與水平方向成60°角斜向上拉木箱，也能使它做勻速直線運動。如圖6所示。則木箱與水平地面的動摩擦因數為

圖6

( )

圖7

【方法點撥】此類題型有一個重要特點就是物體受到的是滑動摩擦力或物體剛要滑動(最大靜摩擦力可近似為滑動摩擦力)，通過摩擦角進行減力，先把四力減為三力，然后運用圖解法即幾何法求解，解題時要明確摩擦角α是接觸面彈力與全反力的夾角，只要動摩擦因數不變，這個摩擦角α就不變。

圖8

( )

圖9

三、慣性力加力法

在非慣性系中，牛頓運動定律并不適用，而在教學實踐中，對于存在非慣性系的題型中，學生常常糾結為什么結論與自己的判斷差之千里，殊不知此時是因為選擇了非慣性系作為參考系。因此，為了思維上的方便，可以假想在這個非慣性系中，除了相互作用所引起的力之外還受到一種由于非慣性系而引起的力，當物體有加速度(可以是加速階段，也可以是減速階段)時，物體具有的慣性會使物體保持原有運動狀態的傾向，而此時若以該物體為參考系，并在該參考系上建立坐標系，看起來就仿佛有一股方向相反的力作用在該物體上,令該物體在坐標系內發生位移，因此稱之為慣性力。

【應用示例3】如圖10，升降機內有一固定斜面，斜面上放一物體，開始時升降機勻速上升，物體相對斜面勻速下滑，當升降機加速上升時

圖10

( )

A.物體與斜面間的摩擦力減小

B.物體與斜面間的正壓力增大

C.物體相對于斜面減速下滑

D.物體相對于斜面勻速下滑

【應用示范】開始時升降機做勻速運動，升降機是慣性系，牛頓運動定律是成立的，物體處于平衡狀態，當升降機加速上升時，物體有豎直向上的加速度，升降機是非慣性系，牛頓運動定律不再成立，因此我們假想物體m受到一個假想的力，即在物體上加一個與加速度的方向相反的慣性力ma，此時以升降機為參考系，那么物體相對于升降機就處于平衡狀態，物體仍勻速下滑，C選項錯誤D選項正確；物體與斜面間的正壓力增大，根據滑動摩擦力公式Ff=μFN可知接觸面間的正壓力增大，物體與斜面間的摩擦力增大A選項錯誤，B選項正確。

【方法點撥】在物體上附加一個力ma(方向與a相反)后而引入的假想力稱之為慣性力，以非慣性系為參考系，若物體相對于其相對靜止，那么該物體從加上一個慣性力后就處于平衡狀態，根據平衡條件規律求解即可。

【小試牛刀】(原創)如圖11，在一升降機內有A、B兩個質量分別為m、2m的物塊A和B、B和升降機地面之間分別用一勁度系數為k的輕質彈簧拴接在一起，彈簧保持豎直，系統處于靜止狀態。現將升降機以加速度g向上加速，A、B物塊相對升降機移動的位移之比為

圖11

( )

A.1∶3 B.1∶6 C.4∶3 D.7∶3

四、等效重力簡化法

等效重力簡化法的主要受力特點是研究對象受重力和另一個恒力，我們可以把這兩個力等效成一個力，這種方法稱之為“等效重力場”。教學實踐中發現學生常在電磁場里才會有這種等效意識，而等效思想是一種常見的科學思維方式，在四力的平衡中應用“等效重力場”進行簡化，之后就可以按照已學過的物理模型規律進行求解。

【應用示例4】如圖12，晾曬衣服的繩子兩端分別固定在兩根等高的豎直桿上，繩子的質量及繩與衣架掛鉤間的摩擦均忽略不計。原來衣服豎直靜止，一陣風吹來，衣服受到水平向右的恒力而發生滑動，并在新的位置保持靜止。則相比原來，在新的位置時

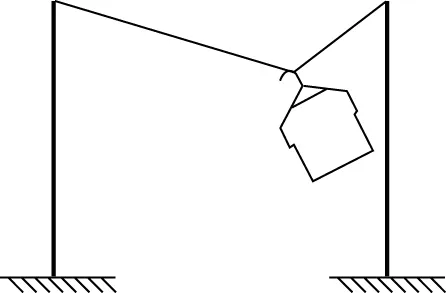
圖12

( )

A.掛鉤左右兩邊繩的拉力不再相等

B.繩的拉力一定不變

C.繩對掛鉤作用力變大

D.繩對掛鉤作用力不變

圖13

圖14

【方法點撥】本題解題關鍵要敏感地捕捉到題設重力與風力都是恒力這一特點，利用等效重力簡化后，與“晾衣服模型”情景一樣，解法異曲同工。本模型對建模能力有一定的要求，這也是新課改所要求的必備能力。

【小試牛刀】(原創)如圖15，粗糙的絕緣平板上放置一根質量m=1 kg、長L=0.5 m的方形金屬棒，其置于豎直向上的勻強磁場中，磁感強度的大小B=4 T，當金屬棒中通以垂直紙面向里I=5 A的電流后，金屬棒處于靜止狀態，現以平板的左端為支點，從右端緩慢抬高平板至平板與水平面夾角為45°過程中，金屬棒相對平板始終處于靜止狀態，則在運動過程中

圖15

( )

A.平板對金屬棒的支持力一直變小

B.平板對金屬棒的支持力一直變大

C.平板對金屬棒的摩擦力一直變小

D.平板對金屬棒的摩擦力先變小后變大

圖16