基于邊界有限元計算方法的多相場重力式大壩動力特性分析研究

張宏美

(浙江湖州宏盈建設工程有限公司，浙江 湖州 313100 )

1 概 述

水資源是人類生存發展的基礎，作為水資源的重要調控設施，水庫的穩定性是保障水資源高效利用的重要基礎[1-3]。水庫的重要組成部分即為大壩，水庫的安全運營與大壩安全穩定性息息相關。已有很多學者針對水庫大壩的靜力穩定性分析作過相當多的研究，極大提高了水庫大壩的建設與設計水平[4-6]。大壩作為重要水利樞紐工程，抗震能力是不可避免需要考慮的重要方面。不同于靜力分析，大壩動力響應是在多相條件下，包括壩基與流水狀態，既有固體場亦有流體場。國內外已有一些學者通過振動臺模型試驗等分析大壩動力反應特征[7-10]；當然在試驗條件不足情況下，上世紀已有一些學者通過解析方法，求解壩體地震反應特征[11-12]。上述兩種研究手段，一定程度上均需要消耗大量的人力物力成本，而數值分析作為高效求解手段，針對于動力反應分析具有較高的匹配性。因而，基于多相場的邊界有限元分析方法[13-15]，求解大壩動力反應特征，為準確評估大壩動力響應穩定性提供重要的理論參考。

2 二維邊界有限元理論

2.1 基本方程

在動力分析理論中，常常會引入邊界元分析理論，并結合有限元離散計算方法，提升求解速率與精確度，為解決工程解析問題提供重要手段。在二維邊界有限元理論中，重定義邊界比例，中心點已不是傳統的零點，其幾何示意圖見圖1。

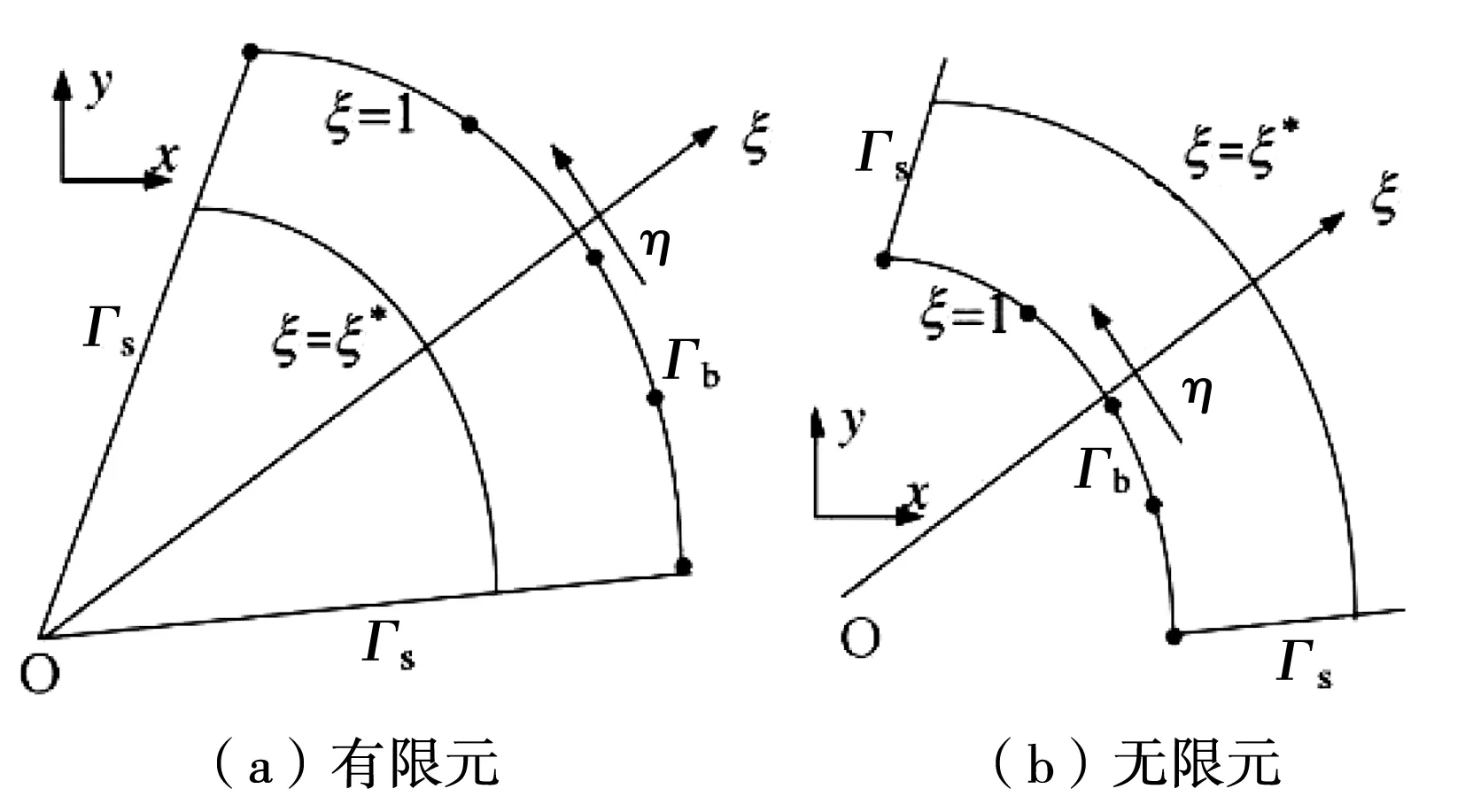
圖1 比例邊界坐標體系

在比例邊界坐標體系中，傳統直角坐標體系中坐標可表述為[16]：

(1)

根據斜率求導原則，可獲得偏微分方程為：

(2)

而邊界有限元坐標體系中，邊界點的坐標可表示為：

(3)

引入雅可比矩陣J，將上式以矩陣形式表述為：

(4)

上式即為邊界有限元中運動矩陣方程，根據上式可演變出靜力問題下的應力與變形解，彈性變形下的應力與變形方程如下：

(5)

(6)

而變形區域內幾何方程為：

(7)

式中：[L]為微分算子式，其代表式如下：

(8)

根據有限元插值理論可知，比例邊界坐標系中邊界與中心點距離可用徑向插值位移表述，其插值服從下式：

u(ξ,η)=u(ξ)N(η)

(9)

聯立上述應力應變以及幾何方程，可得坐標系中幾何統一方程為：

(10)

式中:B1、B2代表系數矩陣，其具體代表式如下：

(11)

物理運動方程可統一表述為：

(12)

2.2 動力控制方程

引入能量做功理論來表述動力運動特征，能量參數的泛函式如下：

(13)

根據材料虛功原理可知，能量泛函式左邊為0，即可得到：

(14)

各分項做功分別為：

(15)

經簡化后可得到：

(16)

式中：系數矩陣均為

(17)

針對二維狀態下的動力平衡方程中，引入慣性力來表述頻域，其控制方程為：

E0ξ2u(ξ),ξξ+(E0+(E1)T-E1)ξu(ξ),ξ-E2u(ξ)+ξ2ω2M0u(ξ)+F(ξ)=0

(18)

式中有：

(19)

動力控制方程的求解需要引入對偶變量q：

q(ξ)=E0ξu(ξ),ξ+(E1)Tu(ξ)

(20)

通過矩陣轉換以及特征值換算，獲得控制方程解為：

(21)

式中：c為常數矩陣。

由于本文分析的是多相場作用下動力反應特征，因而劃分單元網格時考慮多場單元體模型，其形函數可表述為：

(22)

根據形函數表述形式，獲得動力特征中應力應變轉換矩陣表達式為：

(23)

因而，可在上述基礎上，獲得比例邊界坐標體系中剛度矩陣K與質量矩陣M分別為：

(24)

3 工程概況

某水庫建設有混凝土重力壩，壩頂最高處達80 m，壩頂寬度為3.5 m，已修建有通行公路，上下游坡度均為0.75，水庫最大庫容可達1 200×104m3，承擔著需水灌溉及工農業生活用水，在枯水期作為空間上水資源調配的重要利器。大壩包括有液壓控制閘門，啟閉度以及高度均由電腦系統精確控制，輸送水資源量可精確到0.01 m3/s，閘門上下游分別設置有陡坎與消力池，減弱大水流對壩體沖蝕作用。壩體整體防滲性較高，通過在上游壩基覆蓋層以上部分設置有厚60 cm的防滲墻，壩身上安置有止水面板以及土工格柵，降低水流對壩體滲漏破壞性。水庫正常蓄水位設計為72.8 m，所有水位設計均按照大壩允許承受荷載計算。由于混凝土施工關乎著重力式大壩安全可靠性，因而采用BIM技術對大壩混凝土施工均進行過多次模擬，獲得混凝土最佳振搗次數為2次，減少由于混凝土裂縫帶來的壩體失穩與滲漏威脅。

根據地址鉆孔資料得知，地區內主要為河漫灘平原，地勢較為平坦，最高點為兩側的丘陵山坡，壩體兩翼巖體處于較穩定狀態，滑坡及坍塌等地質災害并不顯著，基巖層為白云質灰巖，在局部壩體區段處還含有夾礫巖，粒徑為15～60 mm，完整性較好，地表出露主要在右側坡體上。表面覆蓋土層包括人工填土、粉質壤土與砂土，其中粉質壤土夾有粉、黏粒，含水量達37%，部分鉆孔取樣顯示有結核，具有韌性表現，分布范圍基本涵蓋壩體所有區段，厚度約為2.2～6.9 m；人工填土主要為種植土，較薄，最厚處僅為2.5 m，夾有細砂結構，析水性較強，即滲透系數較低，分布并不均勻，密實性相差較大，部分地段密實度較高；砂土與卵石相交織，其中取樣表明卵石含量約占該深度取樣總重的51.0%～88.4%，砂土屬全新統，分析表明卵石可能是由于水流搬運作用，從上游補充水源河流沖擊搬運至該處，并持續沉積。根據進一步調查發現，由于區域內所處板塊間，因而考慮地震動響應特征很有必要。

4 多相作用下動力分析

4.1 模型建立

以壩體平面狀態作為建模基礎，壩基作為剛性變形體，以SOLID65作為其基本單元體模型，壩體采用PLANE42模型，利用ANSYS建立數值模型。圖2為大壩樁號1+150～1+160區段的數值模型圖，該區段劃分單元體網格，共獲得18 368個，節點數16 538個，動荷載通過引入地震荷載開展分析。

4.2 計算結果分析

為分析方便，本文給出地震動響應特征解析解與邊界有限元計算結果對比，為評價邊界有限元方法的科學合理性提供重要依據。以壩體-水壓力、壩體-壩基的兩相場以及壩體-水壓力-壩基三相場分別進行計算分析，根據相場特點，與圖2建模類似，分別取其中壩體段開展計算分析。

圖2 數值模型圖

4.2.1 壩體-流水兩相場

通過施加地震動荷載后，獲得各階荷載下自振頻率。本文以一階自振頻率下不同反應系數下動水壓力的變化曲線作為對比分析參數，其計算結果見圖3，其中一階自振頻率為32.31 rad/s。

圖3 不同反應系數下動水壓力的變化曲線

從圖3可看出，反應系數為0.25時，曲線相關系數達到0.99，即邊界有限元計算結果與解析解基本一致，動水壓力整體上呈從壩踵至壩頂，動水壓力逐漸降低，在壩踵處，基于邊界有限元方法計算出的動水壓力最大可達到0.026 5 MPa，與高程0.8H處時相比來說下降52.8%；當反應系數為0.5時，壩踵處動水壓力為0.037 MPa，相比反應系數0.25時增大39.6%，反應系數0.5時壩體高程上動水壓力分布基本與小反應系數時基本一致；當反應系數增大至0.75，甚至更大的0.925時，動水壓力在高程上分布趨勢并未發生較大改變，且壩踵處動水壓力分布呈現隨反應系數增大逐漸增大，其中反應系數0.925時壩踵動水壓力相比反應系數0.25時增大326.4%，達到0.113 MPa。

圖4為一組激勵頻率下壩體動水壓力分布曲線。

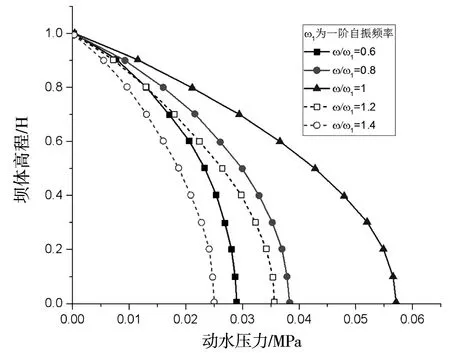
圖4 一組激勵頻率下壩體動水壓力分布曲線

從圖4中可看出，最大動水壓力曲線出現在激勵頻率與自振頻率相等時，即壩體出現自振現象，動水壓力在壩體上分布處于最高，且壩踵處為動水壓力中分布最大值。由于壩踵處動水壓力分布最大，給出不同激勵頻率下壩踵處動水壓力變化曲線，見圖5。

圖5 不同激勵頻率下壩踵處動水壓力變化曲線

從圖5中可看出，隨著激勵頻率變化，動水壓力整體變化呈先增大后逐漸降低，其中最大動水壓力出現在一階自振頻率時，即頻率5 Hz下動水壓力最大，達0.058 MPa。在該頻率后，壩踵動水壓力逐漸降低，但當降低至二階自振頻率時，會出現陡降現象，即頻率15 Hz時，下降幅度超過70%，且在二階自振頻率后動水壓力持續處于較低水平。綜上分析表明，兩相場條件下，壩體動水壓力分布受地震動荷載頻率與動力反應系數影響，壩踵處動水壓力乃壩體上最大值。

4.2.2 壩體-水壓力-壩基三相場

前文計算結果為兩相場條件下壩體動力反應特征，但壩體在一定程度上能否抗震，很大程度上取決于壩基的穩定性，故而將壩基納入分析動力反應特性中很有必要。即構建起三相場條件下動力反應體系，壩體區段取圖2所示的數值模型，相關參數按照土工試驗結果給定。

為分析方便，本文給出大壩兩個特征點處X、Y相位移時程曲線，兩個點分別是壩頂與下游坡度變化點，見圖6和圖7。

圖6 壩頂位移時程曲線

圖7 下游變坡點位移時程曲線

從圖6和圖7中可看出，壩頂處X向位移值整體高于Y向位移，在時間為第二個峰值點時，即時間1.2 s,X向位移達到0.066 m，Y向位移僅為前者的30.3%；同理，在谷值點時亦是如此，在第二個谷值點處，Y向位移達到負方向的0.017 m，而X方向相比增長2.2倍，達到0.054 m。從X、Y向位移整體來看，各振蕩次數下的峰值點位移、谷值點位移之間的周期基本相近，且振蕩表現逐漸趨于穩定，即邊界有限元所計算出來的位移時程結果整體是穩定的。相比壩頂處位移結果，下游變坡點位移整體表現與之一致，不論是X向亦或是Y向，均處于較為穩定狀態；從位移量值來看，下游變坡點位移值亦是X向位移高于Y向位移，在第二個峰值位移點時，X向位移高出Y向位移4.5倍，且谷值點處亦是相差近5倍，即變坡點處X向與Y向位移間差距相比壩頂處更大。

5 結 論

針對重力式大壩動力響應特性問題，引入邊界有限元動力分析方法，計算獲得兩相場與三相場條件下大壩動力特征，結論如下：

1) 基于邊界有限元動力理論計算的結果與解析解基本一致，不論動力反應系數如何變化，兩者結果均一致，相關系數均超過0.99，邊界有限元理論對多相場重力壩求解具有較高的自適應性。

2) 一階自振頻率下動水壓力從壩踵至壩頂逐漸降低，反應系數為0.25時壩踵動水壓力最大，達0.026 5 MPa，而高程0.8 H時降低52.8%；當動力反應系數增大時，壩踵處最大動水壓力逐漸增大，反應系數0.925時壩踵動水壓力相比反應系數0.25時增大326.4%。

3) 當激勵頻率與自振頻率一致時，壩體動水壓力最高；隨激勵頻率增大，壩踵處動水壓力呈先增大后逐漸降低，其中最高點位于一階自振頻率時，達0.058 MPa，二階自振頻率時動水壓力會出現陡降，降低幅度超過70%。

4) 三相場條件下X、Y向位移周期與相位均穩定，且壩頂與下游變坡點均呈X向位移高于Y向位移，第二個峰值點時，壩頂處X向位移達到0.066 m，Y向位移僅為前者的30.3%，但下游變坡點兩者差距4.5倍，X、Y向位移間差距比壩頂處更大。