均布徑向荷載下雙鉸蜂窩鋼拱的撓度研究

袁偉斌,許雷池

(浙江工業大學 土木工程學院，浙江 杭州 310023)

1910年， Chicago Bridge & Iron Company首先開發了蜂窩構件，與材料用量相等的實腹構件相比，前者的截面高度更高，繞強軸的慣性矩更大。腹板開孔鋼拱(簡稱蜂窩拱)是一種新型的鋼結構構件，結合了蜂窩梁和拱的特點，也開始在大跨度空間中應用開來，如航站樓、體育館、展覽館等。蜂窩構件因其腹板孔洞的存在，其剛度沿軸長方向不再具有連續性，導致其理論分析難度陡增。早先假定蜂窩梁的結構性能和實腹梁相同，取其最薄弱空腹截面的抗彎剛度作為計算剛度[1]。但此方法誤差過大且不能反映蜂窩梁的受力特點。Altfillisch等[2]較早提出了空腹桁架理論，其將蜂窩梁比擬為剛節點桁架來計算蜂窩梁的正應力和撓度。此方法至今仍為通用，后來的學者在此基礎上不斷改進[3-5]。隨著計算機技術的發展，數值分析方法逐漸受到廣泛應用。朗婷等[6]用有限元法研究了蜂窩梁的受力性能和應力分布特點。鄭懿等[7]也采用有限元法對蜂窩梁的撓度影響因素進行了分析。袁偉斌等[8-10]采用能量法對蜂窩構件進行了理論研究，其中提出可將蜂窩構件當作夾層構件來進行分析。

上述的研究均是針對蜂窩直梁或柱，對于蜂窩拱的研究相對較少，目前對蜂窩拱的分析主要通過數值模擬和實驗研究[11-13]，缺少理論研究。筆者借鑒文獻[9]的方法，建立了蜂窩拱的總勢能方程，對均布徑向荷載作用下的兩鉸蜂窩拱的撓度公式進行了推導，并采用ABAQUS有限元軟件進行了求解驗證，為蜂窩拱的結構設計提供了重要的參考價值。

1 相關研究

蜂窩構件由于腹板存在孔洞，構件的剛度沿軸長方向呈現非連續性，導致不能直接使用相應的實腹計算公式。由于蜂窩構件與夾層構件受力機理相似，所以可以將蜂窩構件當作夾層構件考慮，將其上下兩層連續部分作為承受彎矩和軸力的表層，中間腹板不連續部分當作承受剪力的夾層。筆者認為對于蜂窩鋼拱的分析亦可采用上述方法，采用圖1(a)所示的坐標系，O為拱的圓心，R為拱軸線的初始曲率半徑；w為徑向撓度，v為切向位移。作如下假設：1) 拱截面高度遠小于初始曲率半徑，則截面上的每個點的曲率半徑都相同；2) 表層橫截面變形后仍然保持平面，且與總軸線垂直，受彎矩和軸力作用；3) 夾層橫截面上各點的切向位移沿截面高度呈線性分布，受剪力作用；4) 橫向的正應變為零。

圖1 結構計算簡圖Fig.1 The structural calculation diagram

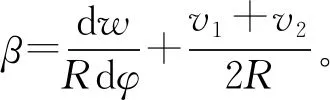
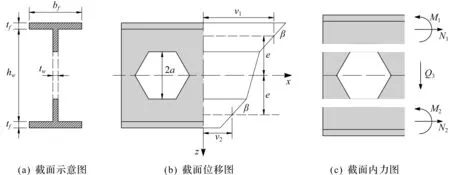
圖2 截面受力狀態Fig.2 The forced state of cross-section

根據圖2(b)可以得到截面上任意一點(φ,z)的切向位移分別為

1) 上部T形截面，即-(hw/2+tf)≤z≤-a時，有

(1)

2) 下部T形截面，即a≤z≤(hw/2+tf)時，有

(2)

3) 中間截面，即-a≤z≤a時，有

(3)

得到的上下T形截面上任一點的切向位移公式，與文獻[14]得到的拱截面上任一點的切向位移公式相同。由于假設了橫向的正應變為零，所以截面上任一點的徑向位移uρ=-w。接著由極坐標中的幾何方程[15]得到相應的應變表達式為

1) 上部T形截面，即-(hw/2+tf)≤z≤-a時，有

(4)

2) 下部T形截面，即a≤z≤(hw/2+tf)時，有

(5)

3) 中間截面，即-a≤z≤a時，有

(6)

由應變表達式可得圖2(c)截面上的內力分別為

(7)

(8)

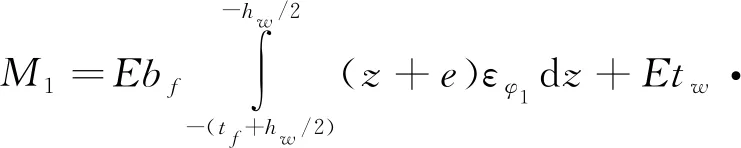
(9)

(10)

(11)

式中：E為彈性模量；G為剪切模量；Atee，Itee分別為T形截面的面積和慣性矩。

拱的應變能表達式為

(12)

式中：l為蜂窩拱的弧長；ksh為腹板不連續部分的剪切修正系數，由于截面高度遠小于曲率半徑，此處認為初始曲率對該系數影響可略去不計。

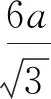
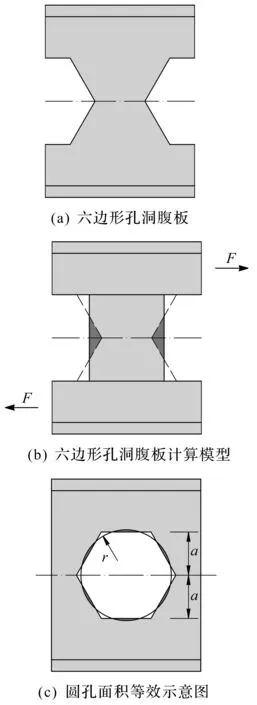
圖3 腹板剪切應變能計算模型示意圖Fig.3 Simple models used for calculating strain energy of web

將式(4～6)代入式(12)得

(13)

當蜂窩拱在均布徑向荷載作用下時，外力做功為

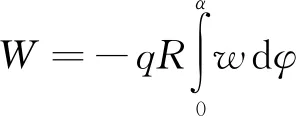
(14)

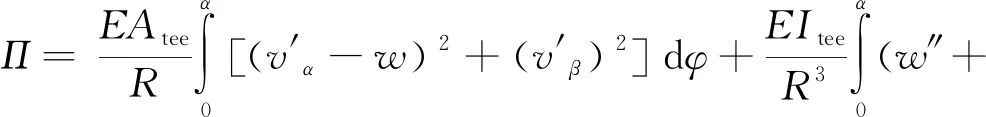
(15)

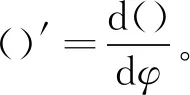
通過觀察式(15)可發現第4項與第3項相似且有數量級上的差距，為簡化計算可忽略第4項。如圖1(b)所示，雙鉸支蜂窩拱在均布徑向荷載下發生正對稱變形，由a位置向b位置變形，設拱在均布徑向荷載下的位移函數為

(16)

式中：A，B，C均為待定常數。

顯然式(16)滿足位移邊界條件：v0(0)=v0(α)=0，w(0)=w(α)=0，w″(0)=w″(α)=0。將式(16)帶入式(15)，根據最小勢能原理由δΠ=0可得

(17)

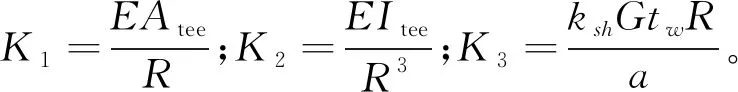
式(17)的解過于復雜，對得到的解再作簡化，認為在一般工程中常用尺寸(矢跨比大于0.1)的雙鉸蜂窩拱在均布徑向荷載下，其上下T形截面自身的彎矩M1和M2相比于軸力N1和N2產生的彎矩可忽略不計。將解略去K2，得到經簡化后的徑向撓度表達式為

(18)

(19)

(20)

經計算分析，對于蜂窩拱常用尺寸(矢跨比在0.1～0.5)的P值一般徘徊在-0.18附近，于是由式(18)可知：對于均布徑向荷載下的兩鉸蜂窩拱撓度的主要影響因素是蜂窩拱的初始曲率半徑以及截面上下T形部分的面積。

2 有限元模型

使用ABAQUS有限元軟件對均布徑向荷載下的兩鉸蜂窩拱的正對稱變形進行模擬分析。為了驗證公式的適用性，對不同模型尺寸下的蜂窩拱進行了模擬，以孔洞大小、矢跨比和長細比作為變量考慮，將截面高度、板厚以及孔間距作為定值，其中長細比通過改變跨度和翼緣寬度間接考慮。采用20×20的S4R殼體單元建立模型，為了計算結果的準確性在孔洞周圍加密網格分布。將端部截面耦合到形心，并限制該點的面內平動來達到鉸支的邊界條件，見圖4。

圖4 基本模型示意圖Fig.4 The basic model diagram

上述模型的彈性模量E=210 GPa，泊松比ν=1/3。通過ABAQUS求得不同模型尺寸下的頂點撓度有限元值F與式(18)計算得到的理論值T分別列于表1之中。表1中所有模型的hw=180 mm，tw=10 mm，tf=10 mm，s=πr，q=10 kN/m。

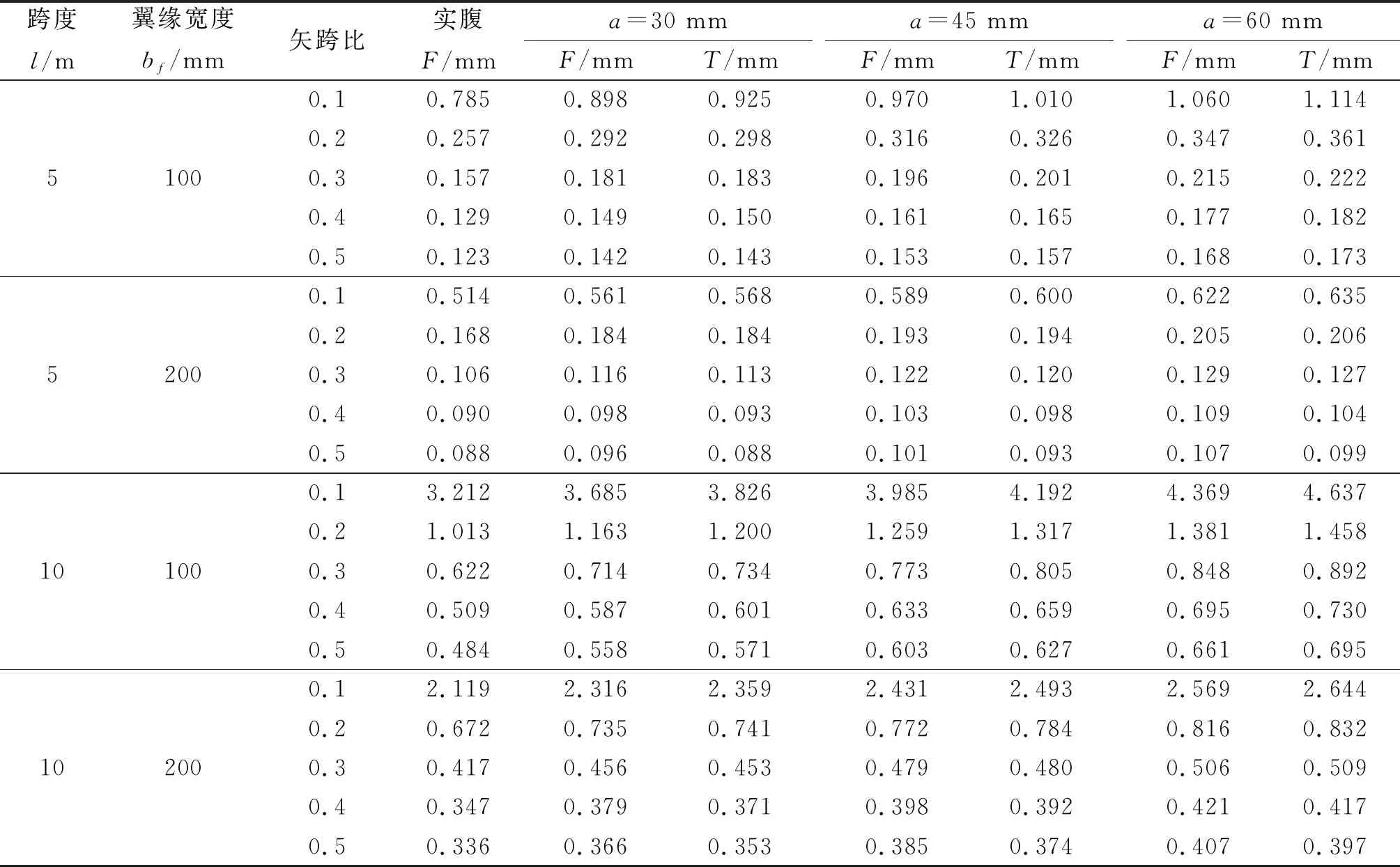
表1 不同模型尺寸下兩鉸蜂窩拱的頂點撓度理論解T和有限元解FTable 1 The theoretical analyses T and FEA F of two-hinged castellated steel arch beams vertex deflection with different sizes

3 分析與對比

圖5，6分別為不同尺寸模型下蜂窩拱的頂點撓度示意圖和理論解與有限元解對比圖，結果表明：當矢跨比在0.1～0.5時，筆者提出的式(18)與有限元數據吻合較好，兩者的相對誤差基本在5%以內，可以滿足常用尺寸的蜂窩拱的實際工程應用，也驗證了筆者對蜂窩拱所采用的假設具有一定的可行性，能有效應用到對蜂窩拱的小撓度理論分析中。圖6中理論解/ABAQUS解的比值隨著矢跨比增大而下降，是由于較大矢跨比的雙鉸拱在均布徑向荷載作用下，其撓曲線偏離筆者所假設的位移函數所致，但仍具有一定精度。圖6還顯示bf=100 mm時孔洞的大小對公式準確性的影響大于bf=200 mm時的影響，說明上下T形截面過小會放大對不連續腹板部分等效產生的誤差，而對正常高寬比的截面計算分析證明筆者采用的等效缺陷并不會導致過大的誤差。由圖5可看出：在均布徑向荷載作用下雙鉸蜂窩拱的孔洞越大、構件越細長，矢跨比越小，則其撓度越大；為減小蜂窩拱的撓度，參考式(18)，在跨度不變的情況下，可以采取提高矢跨比或增大上下T形截面面積的措施。

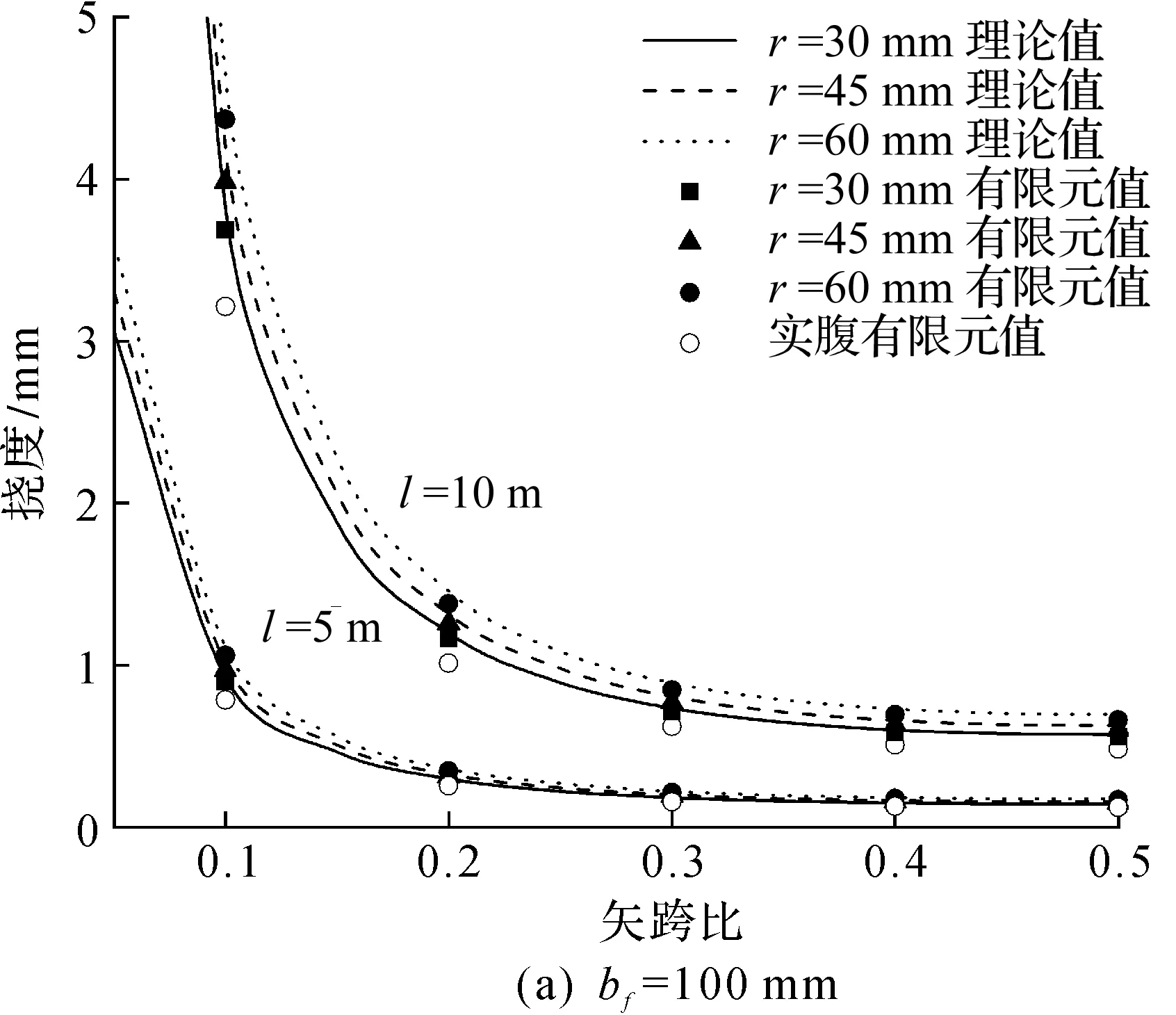
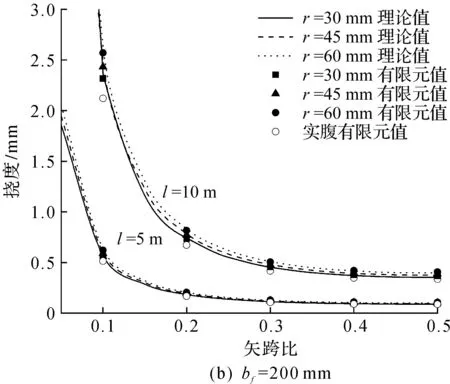
圖5 不同尺寸下頂點撓度示意圖Fig.5 Diagram of vertex deflection with different sizes

圖6 理論與有限元頂點撓度對比圖Fig.6 Comparison of vertex deflection between the theoretical analyses and FEA

4 結 論

對均布徑向荷載下的雙鉸蜂窩拱的撓度進行了研究，將夾層梁理論應用到蜂窩拱中，根據最小勢能原理推導了出相應的撓度公式。并采用ABAQUS有限元軟件對公式的適用性進行了探討，結果顯示兩者吻合較好，其精度可滿足實際工程使用。同時也驗證了筆者對蜂窩拱分析中所采用的一系列假設的可行性，能有效應用到蜂窩拱的小撓度理論分析中。最后，提出在跨度不變的情況下，可采取提高矢跨比或增大上下T形截面面積的措施來減小均布徑向荷載作用下雙鉸蜂窩拱的撓度。