基于正弦擬合的空間目標短弧關聯算法

黃秋實，張雅聲,*，馮飛

1. 航天工程大學，北京 101400 2. 北京跟蹤與通信技術研究所，北京 100094

隨著各國的航天發射活動日益活躍，全球航天器的數量呈現激增趨勢。與此同時，大量的空間碎片也威脅著地球同步軌道(geosynchronous orbit, GEO)航天器的運行安全[1]。2002年，美國國防部曾提出控制空間的三大能力，分別是空間態勢感知能力、進攻性空間對抗能力及防御性空間對抗能力。其中空間態勢感知是探索太空及維護太空安全的基礎。空間目標監視系統是空間態勢感知的重要組成部分，其功能包括對空間目標識別、搜索、跟蹤、編目以及定軌等。美國的空間目標監視能力全球領先，地基與天基的監視系統均在建設和不斷發展中，同時也耗資巨大。以天基空間監視系統SBSS為例，3～8顆監視衛星的組網預計耗費8.58億美元。天基監視系統不受地球大氣的影響以及地球曲率的制約，功耗低，體積小，可以很好地與地基監視系統相互補充[2-3]。中國的天基監視系統亟待進一步的發展。筆者所在的實驗室提出了天基泛在感知的概念，旨在利用衛星裝備的星敏感器，在星敏感器定姿過程中拍攝的星圖中檢測和提取空間目標，并從大量數據中挖掘空間目標可用的觀測信息，實現空間目標的監視，可節約發射專用監視衛星的成本[4]。與專用型監視衛星的跟蹤觀測模式不同，泛在感知系統依靠星敏感器視場和目標的自然交會捕獲目標[5]。雖然每次連續觀測的時間短，但星敏感器數量多，可實現對空間目標斷續的在不同觀測幾何下的短弧觀測[6]。文獻[4]可依靠星敏感器提供的僅測角數據實現對空間目標的定軌，該方法的前提是實現空間目標的關聯，以便將相同目標的測角數據應用于計算。本文要解決的重點問題是將星敏感器斷續觀測到的空間目標進行關聯，并且能適應短弧觀測下的關聯需求。

1 問題描述

現役衛星大多正交安裝兩臺星敏感器，因此衛星運動過程中，多臺星敏感器的視線會自然交會，如圖1(a)所示，并且空間目標在運動過程中會斷續地進入多批星敏感器的視場，如圖1(b)所示。高軌的空間目標的星等為10～12，主流星敏感器視場超過10°且極限探測星等為5.5～7。當前中國有種研創階段的星敏感器的特點是小視場、高極限探測星等。文獻[7]提出了一種以太陽同步軌道星敏感器為主的GEO監視的構型。選擇12顆太陽同步軌道衛星、12顆晨昏太陽同步軌道衛星、4顆45°軌道傾角的衛星作為觀測平臺，進行星敏感器視場自然交匯模式下的GEO監視能力仿真，重點分析對[-15°,15°]緯度帶內的GEO目標的觀測效能。仿真時間為2020年3月20日00：00至2020年3月21日00：00，星敏感器的視場為2°×2° 觀測效能如圖2所示。

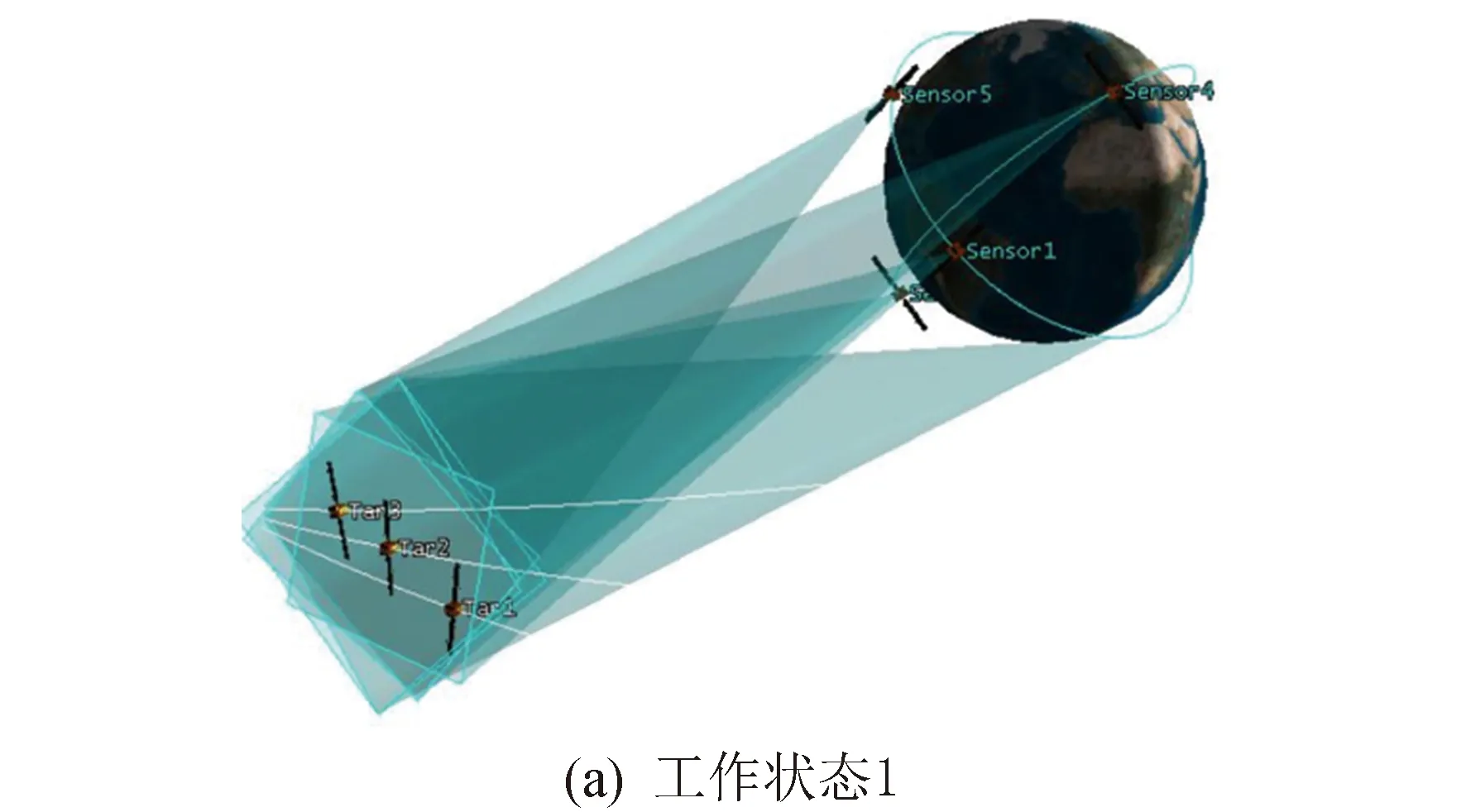
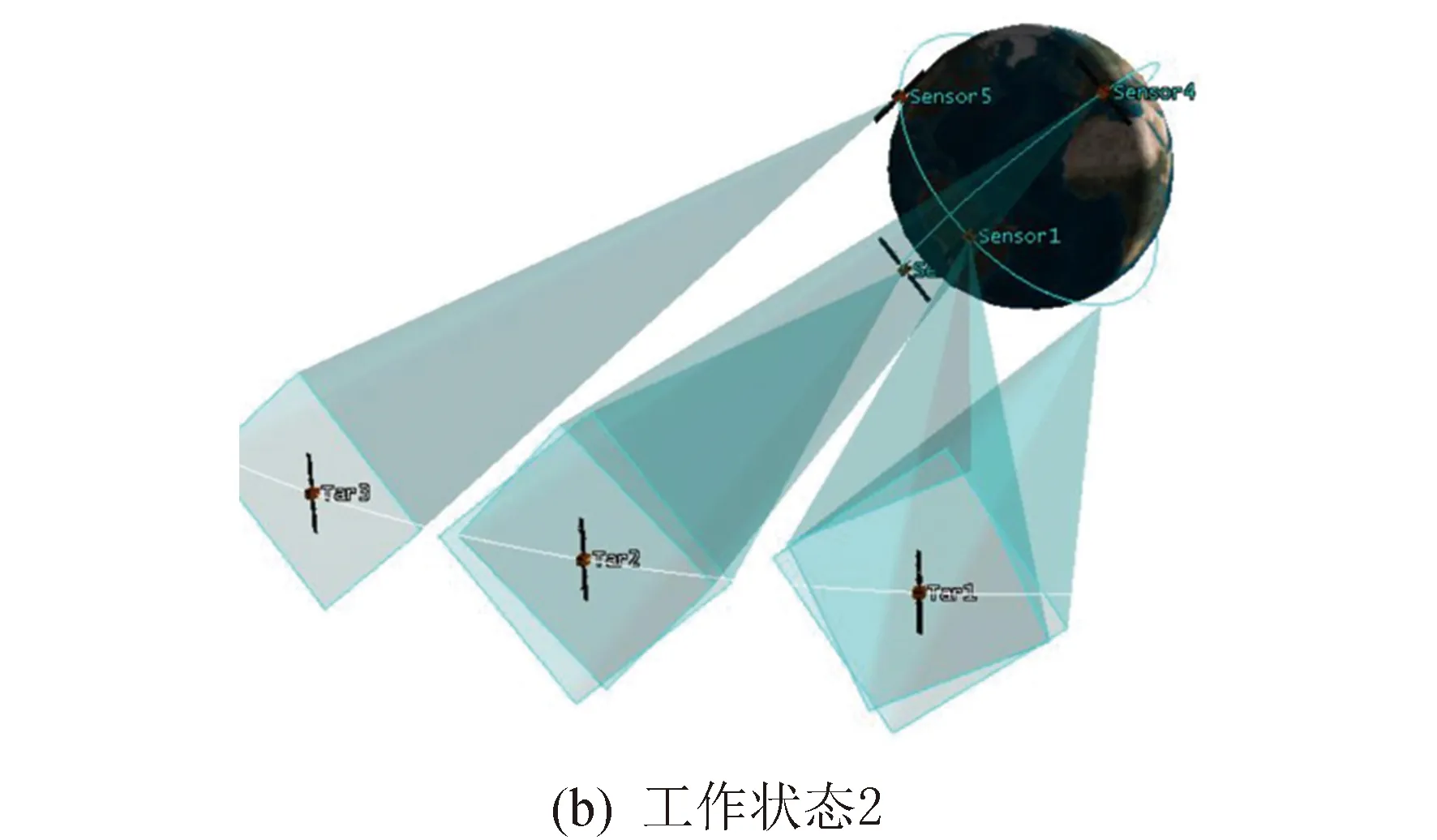
圖1 星敏感器用于目標監視的工作狀態Fig.1 Star sensor working status for target monitoring

圖2(a)為[-15°,15°]緯度帶內各區域同時觀測的星敏感器的數目，可以看出95%的區域可以被超過兩臺星敏感器同時覆蓋，且目標重訪間隔為20～50 min。圖2(b)為各區域目標的最大觀測時長，可以看出部分區域最大觀測時長小于180 s，難以通過短暫的觀測確定目標初始軌道。本文重點解決短弧觀測小的目標關聯問題，將不同時間段多星敏感器對空間目標的短弧觀測進行關聯，找到屬于同一目標的觀測。

空間目標中斷航跡關聯的一般思路是根據新舊航跡的觀測值推算空間目標軌道并獲得新舊航跡相同時刻的狀態估計，依靠歐式距離、馬氏距離、模糊隸屬度等指標評估新舊航跡的相關性[8]。由于星敏感器僅能提供對于目標的測角數據，此方法需要較長的觀測時間以確定空間目標的初始軌道，當采用小視場星敏感器時，空間目標在星敏感器視場中停留時間過短，不足以確定初始軌道。文獻[9]結合星敏感器在視線交匯

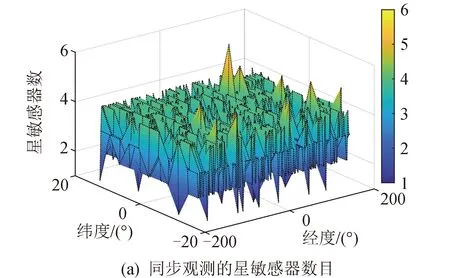
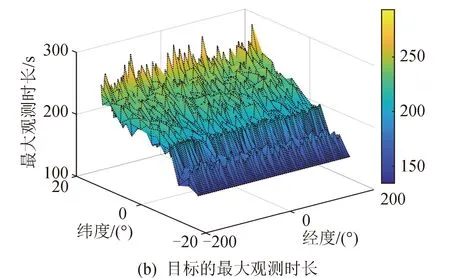
圖2 星敏感器自然交會觀測效能Fig.2 Observation efficiency of natural intersection of star sensors

時協同觀測的工作狀態，基于對極幾何約束實現了空間目標的同步關聯，并獲得測角信息以及距離信息，確定空間目標的位置。意大利學者Milani提出了容許域的概念[10]，在測量斜距和斜距變化率構成的二維平面對空間目標運動加以約束，可用于短弧光學測量的初始軌道估計。在實際應用中發現，將容許域進行剖分并搜索與觀測值最接近的初軌運算復雜度較高，而且由于觀測時間短和誤差的存在，搜索的最優軌道與目標真實軌道可能有較大偏差，影響了關聯準確率[11-13]。

目前對于空間目標短弧關聯的主要思路有兩種：一種是在容許域內搜索最符合短弧觀測的軌道作為空間目標初軌，再利用軌道外推至關聯時刻，以馬氏距離作為關聯準則[14]；另一種是假設兩端短弧為同一目標軌跡，利用邊界條件求解假設條件下的軌道，將求得的軌道與實際觀測進行對比[15]。上述兩種方法都需要對空間目標航跡進行軌道確定，本文旨在提出一種無需定軌，僅依靠新舊航跡的觀測值就可較準確判斷航跡是否來自同一目標的短弧關聯算法。

2 基于正弦擬合的空間目標短弧關聯算法

根據大量對GEO的觀測數據，空間目標在J2000坐標系下的赤緯會隨著赤經呈現正弦分布，峰值近似為軌道傾角，即使是軌道傾角為0°的GEO軌道，如圖3所示的GEO1也會呈現出峰值較小的正弦分布規律。

圖3 空間目標目標的赤經赤緯關系Fig.3 Right ascension and declination relation of space target

嘗試從軌道動力學角度推導上述規律。如圖4所示為航天器星下點的球面幾何圖，在J2000坐標系下，X軸指向平春分點，i,ω,f,Ω分別代表軌道的傾角、近地點俯角、真近點角、升交點赤經，α,δ代表空間目標的赤經赤緯。根據赤經赤緯定義，SD所在的平面垂直于ND所在平面，因此二面角∠SDN為直角，∠SND=i(i∈[0,0.5π]),球面三角形SDN為直角球面三角形。根據球面三角形的性質可以得到：

tanδ=tanisin(α-Ω)

(1)

δ=arctan[tanisin(α-Ω)]≈isin(α-c)

(2)

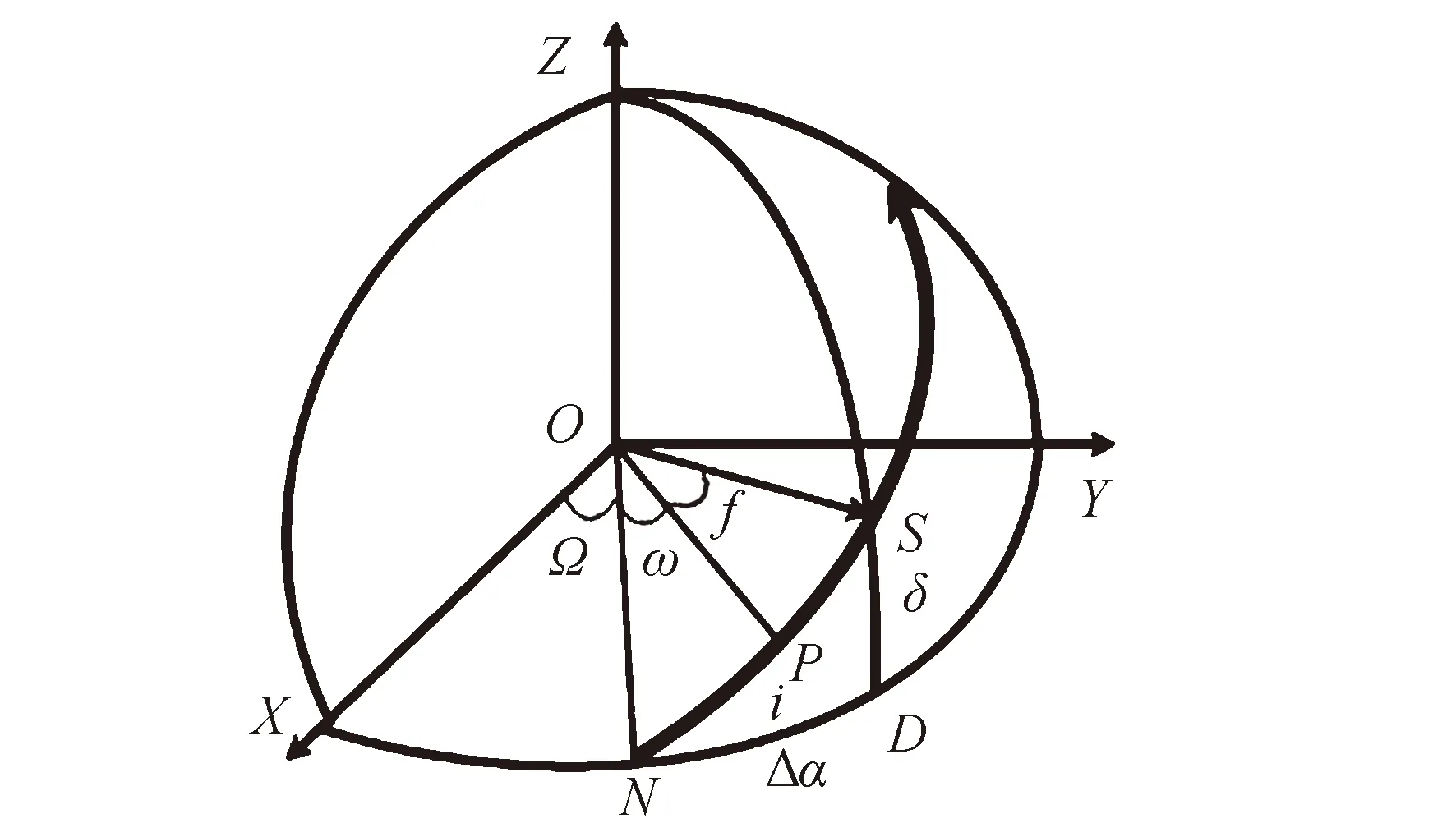
圖4 航天器星下點球面幾何示意Fig.4 Spherical geometry of spacecraft sub-satellite points

式(1)中tanδ∈[-tani,tani]，δ∈[-i,i]。由于空間目標運行一周赤經的變化為360°，式(2)中復合函數的周期也為360°。因此赤緯隨赤經的變化可由正弦型函數表示，c為常數。

經統計80% GEO目標的軌道傾角小于1°。當軌道傾角i<1° ，有c=Ω。證明如下：

arctan[tanisin(α-Ω)]-isin(α-Ω)=

tanisin(α-Ω)-isin(α-Ω)-

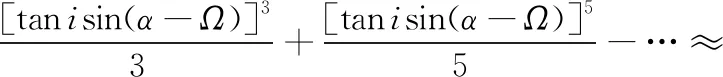
isin(α-Ω)≈0

因此可以驗證基于GEO觀測數據擬合的函數表達式的推測，GEO目標赤緯隨赤經變化近似為正弦函數，且峰值與軌道傾角接近。

當獲得空間目標在J2000坐標系下的赤經赤緯的觀測值，根據間斷短弧觀測間的正弦擬合情況，判斷新舊航跡的目標是否來自于同一軌道。

2.1 基于星敏感器的空間目標協同定位算法

星敏感器用于空間目標監視任務時，通常在多臺星敏感器視場重疊時對目標觀測[16]。因此首先需要將同一時刻多臺星敏感器視場中的相同目標關聯。由于空間目標距星敏感器較遠可抽象成一點，兩臺星敏感器對空間目標觀測的幾何構型如圖5所示，根據多視圖幾何相關原理，同一空間目標在兩臺星敏感器成像的像素坐標需滿足對極幾何約束：

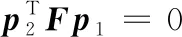
(3)

其中p2和p2代表空間目標在星圖上的像素坐標，第3維補1占位。F為3×3的基礎矩陣，與星敏感器的位置，星敏感器坐標系的旋轉關系，及星敏感器參數有關。星敏感器位置、姿態已知則F可求。將不同星圖中像點坐標分別帶入式 (3)，計算結果越接近0，兩像點為同一目標概率越高。目標關聯示例如圖6所示。

確定測角數據來自同一目標后，當同步觀測的星敏感器數量為2臺，可根據雙目視覺原理求出空間目標的具體位置，當數量大于2時可根據最小二乘求解。

星敏感器提供的測角數據(α,δ)代表J2000坐標系下的空間目標相對星敏感器的赤經、赤緯。在J2000坐標系下，某一時刻空間目標的三維坐標為r(x,y,z)，第i個星敏感器在空間坐標為Ri(Xi,Yi,Zi)。星敏感器到空間目標的方向向量和向量的模分別為ρ和ρ。根據觀測幾何可得：

r=ρρ+Ri

(4)

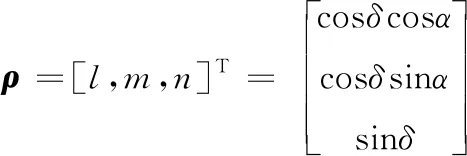
(5)

為消除未知量ρ的影響,在式(4)兩側同時叉乘向量ρ,得到：

r×ρ=Ri×ρ

(6)

展開得到：

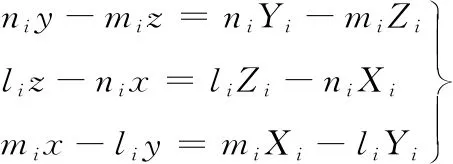
(7)

同一時刻目標的位置矢量r(x,y,z)為未知量，將其寫成線性方程組的形式：

A·X=b

(8)

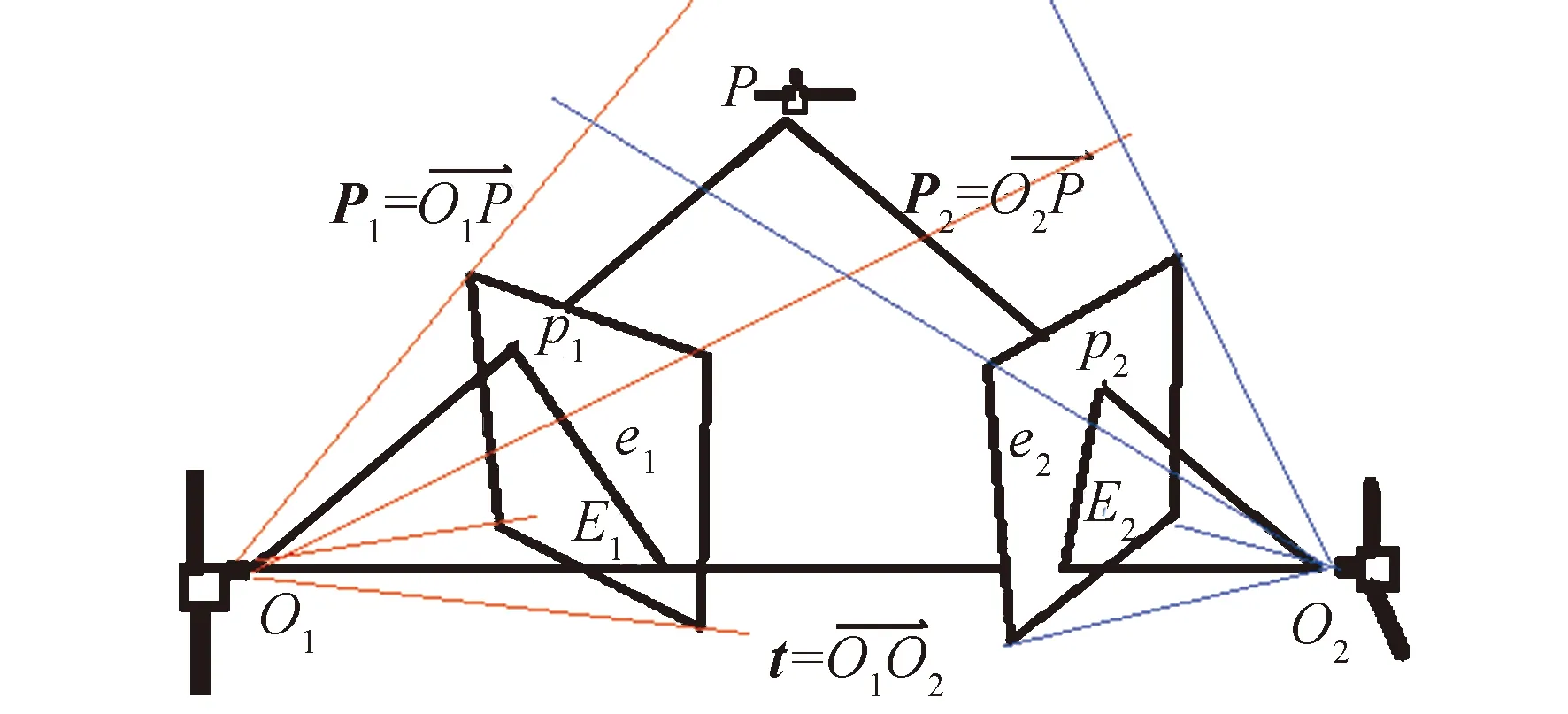
圖5 星敏感器同步觀測幾何構型Fig.5 Geometric configuration of star sensor synchronous observation

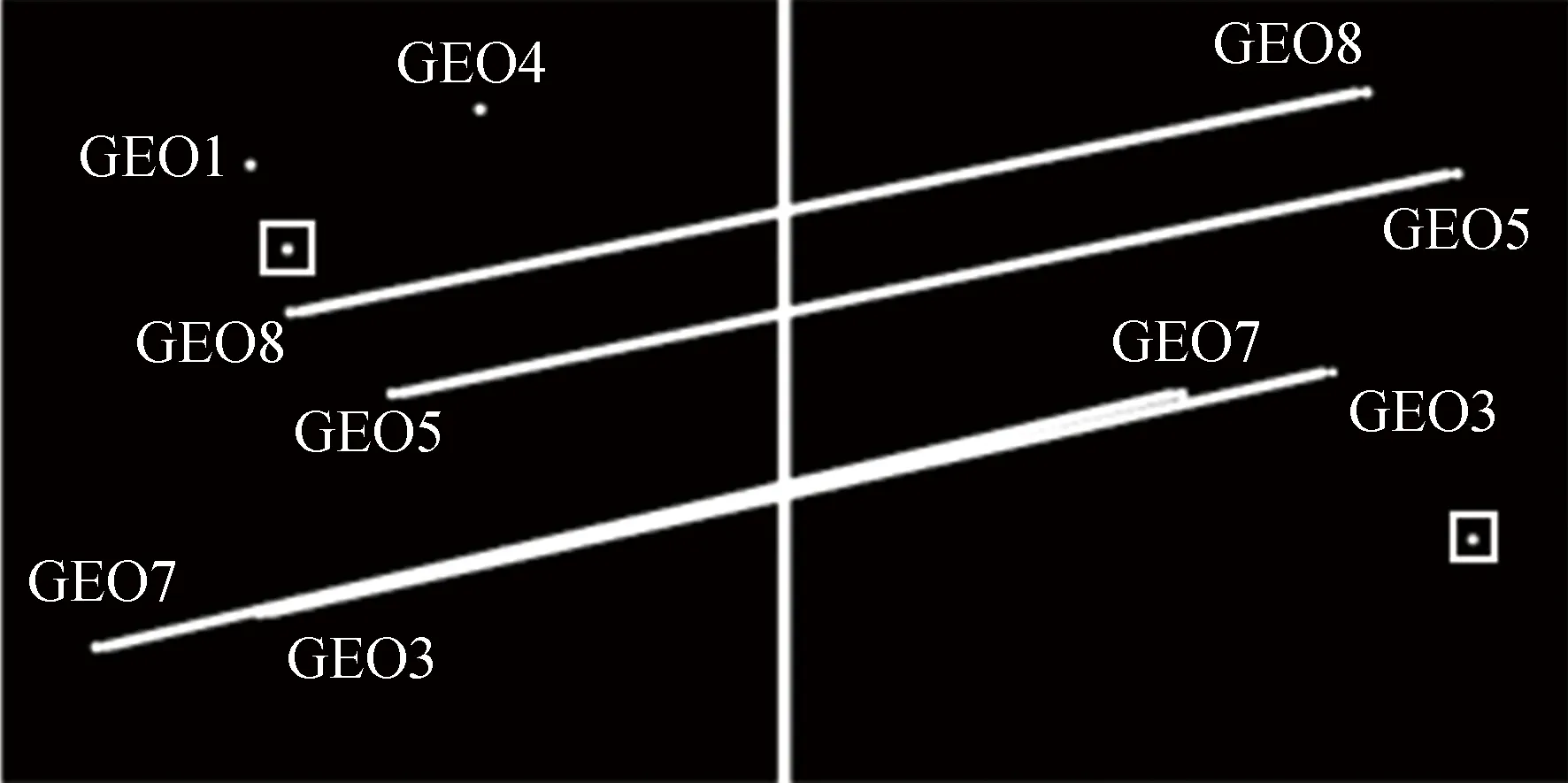
圖6 空間目標同步關聯示例Fig.6 Example of space target synchronization association

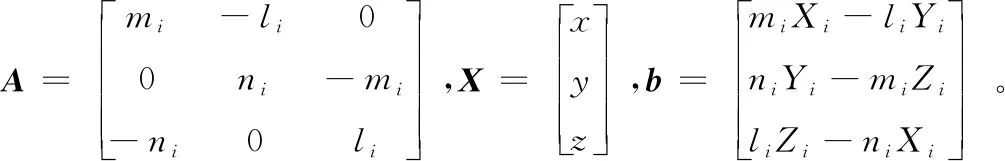
X=(ATA)-1ATb

若空間目標在J2000坐標系下的赤經赤緯為(α0,δ0)，

2.2 基于正弦擬合的目標關聯

由于一些重要的通信、廣播、數據中繼衛星均分布在GEO軌道，因此GEO軌道上的目標關聯是重點研究對象，根據美國優思科學家聯盟對在軌航天器的實測數據分析，80%的GEO軌道傾角小于1°且都為近圓軌道，98%的GEO偏心率小于0.007。圖7展示了GEO軌道在J2000坐標系下分布密度，將赤經赤緯平面等分成100塊，統計各塊內GEO的數目。數目越大越接近紅色，代表空間目標越密集，其中赤經[-160°,-150°]是GEO目標最密集的范圍，赤經[-100°,-40°]僅有個別GEO目標，在衛星工具包(Satellite Tool Kit, STK)軟件上觀察，發現上述區域分別位于中亞和太平洋上空。赤緯0°附近有一條密集的GEO目標帶，對此GEO帶上的目標關聯是研究的重點。

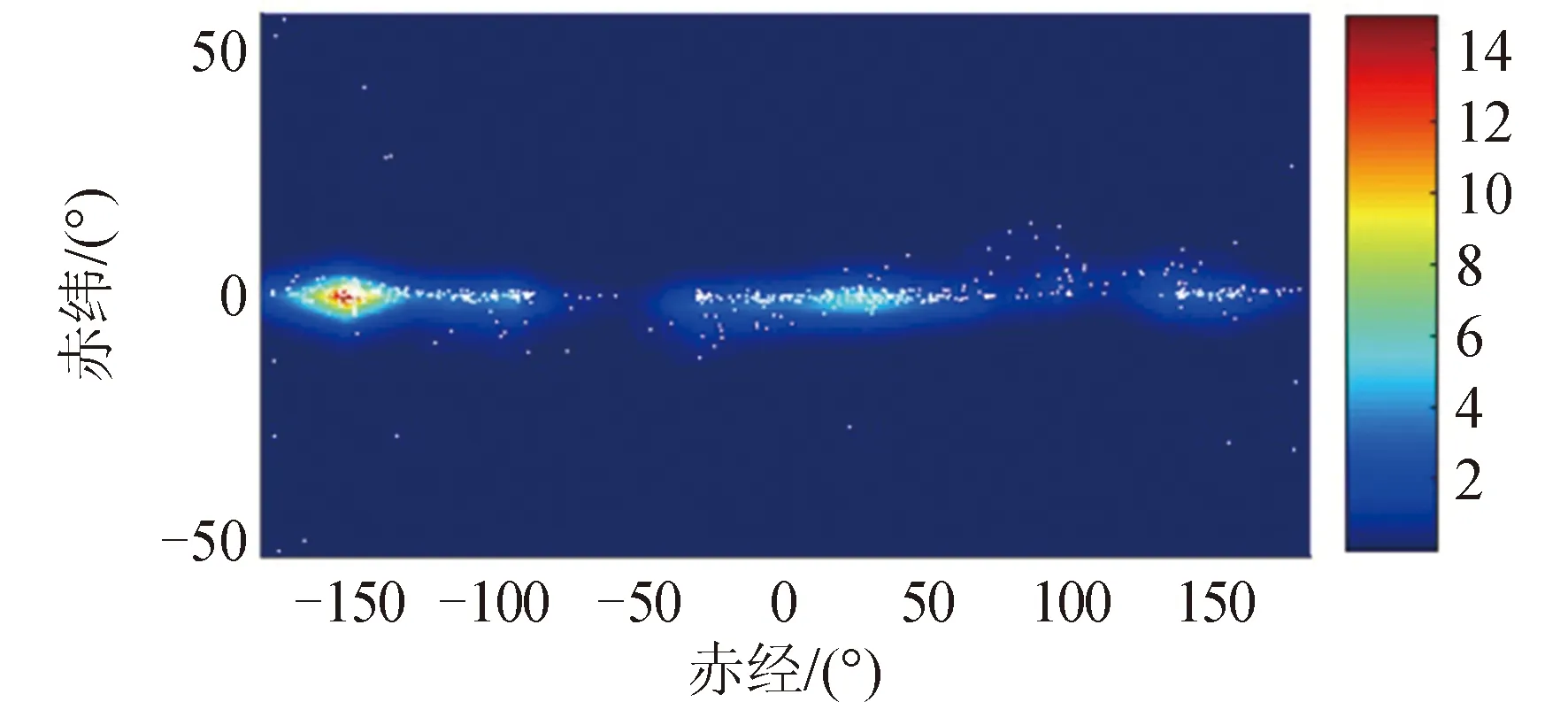
圖7 GEO分布密度Fig.7 Distribution density of GEO

若J2000坐標系下，地心到舊航跡的起點向量為rold, 地心到新航跡的起點向量為rnew,新舊航跡采樣點與地心距離的集合r中最大值為rmax，最小值為rmin，單位為km。兩向量夾角〈rold,rnew〉為θ，單位為(°)，T為新舊航跡間隔時間，單位為h。根據GEO目標運動特性加入軌道半徑和角速度約束條件：

(9)

(10)

當GEO目標偏心率小于0.007，間隔時間T≤12 h時，空間目標與地心距離的變化量小于或等于50 km/h×Tkm。當T>12 h時，空間目標與地心距離變化量小于或等于600 km。

每一時刻，空間目標在J2000坐標系下的赤經赤緯為(αt,δt),因此目標的新舊航跡的觀測采樣值均落在以赤經為x軸，以赤緯為y軸的平面直角坐標系上,赤經赤緯的單位均為(°)。由于赤經的范圍為[-180°，180°]，因此空間目標在運動過程中赤緯隨赤經變化趨勢為周期為360°的正弦曲線，對新舊航跡觀測采樣進行正弦擬合：

y=asin(x+b°)

(11)

若殘差平方和在閾值范圍內，即：

SSE≤ε

(12)

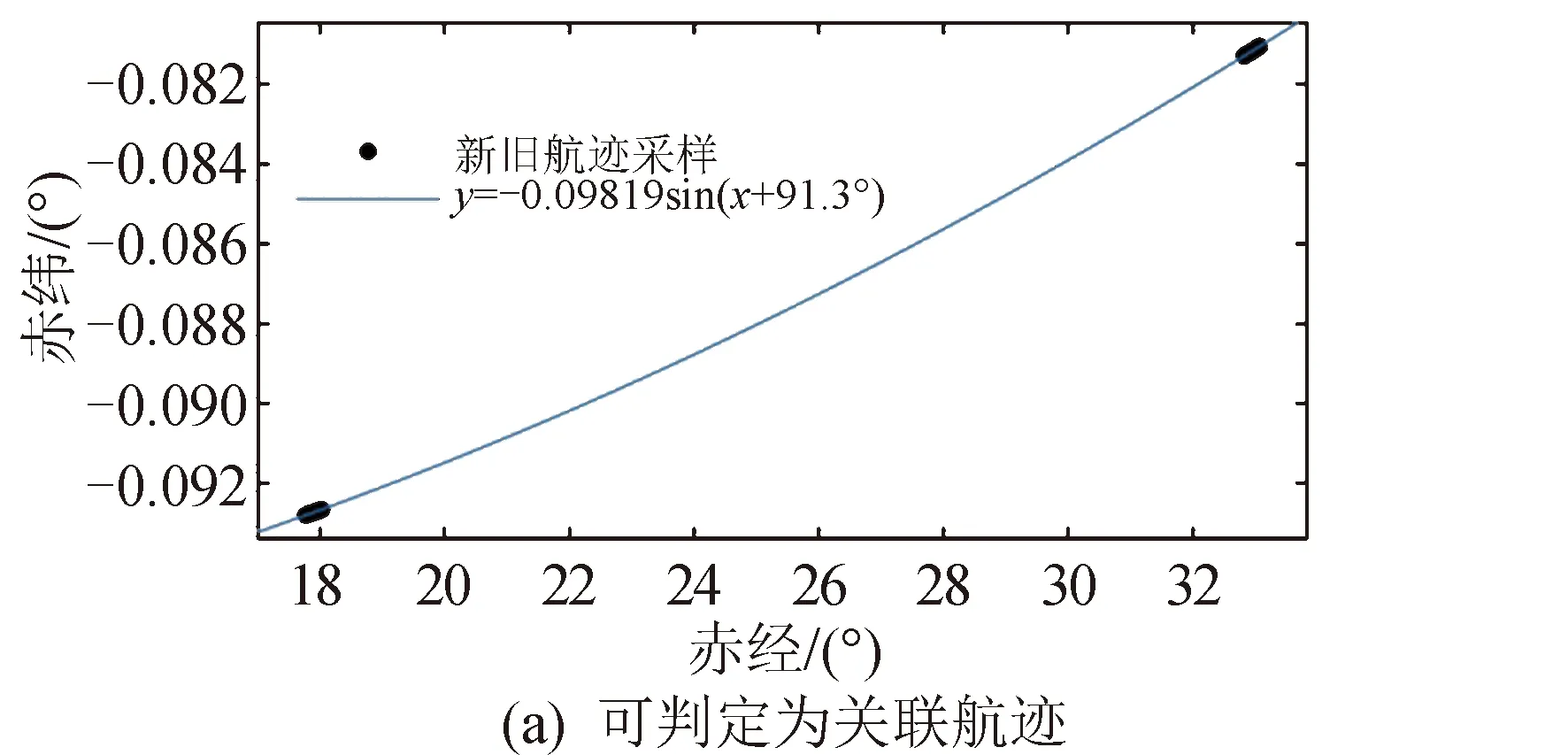
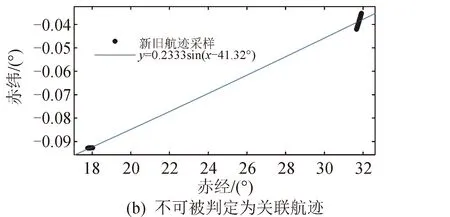
圖8 中斷航跡的擬合關聯Fig.8 Fitting of track segments

可初步認為新舊航跡來自同一條軌道，如圖8所示。對上述關聯進一步檢驗并進行多義性處理，保證每條舊航跡最多與一條新航跡關聯，每條新航跡最多與一條舊航跡關聯，最終將正弦擬合殘差平方和最小的新舊航跡定義為關聯航跡。以m行n列矩陣A匯總關聯結果，其中元素aij代表第i個舊航跡與第j個新航跡的關聯結果。aij為0代表新舊航跡不關聯，即來自不同目標，aij為1代表新舊航跡被判斷為關聯，可認為其來自同一目標[17-18]。

3 仿真校驗

3.1 多星敏感器協同定位精度仿真

仿真利用STK平臺搭建場景，進行200次的空間目標定位仿真，比較并計算出的空間目標赤經赤緯與真實值的偏差如圖9和表1所示。分析可知利用星敏感器協同定位誤差的主要來源分別是星敏感器所在衛星的位置誤差與星敏感器對空間目標觀測的測角誤差。因此仿真中引入了3組不同水平的高斯白噪聲(1″，100 m)，(2″，100 m) ，(2″，1 000 m)，分別代表星敏感器測角誤差的標準差為1″，2″，2″，星敏感器自身位置誤差的標準差為100 m，100 m，1 000 m。

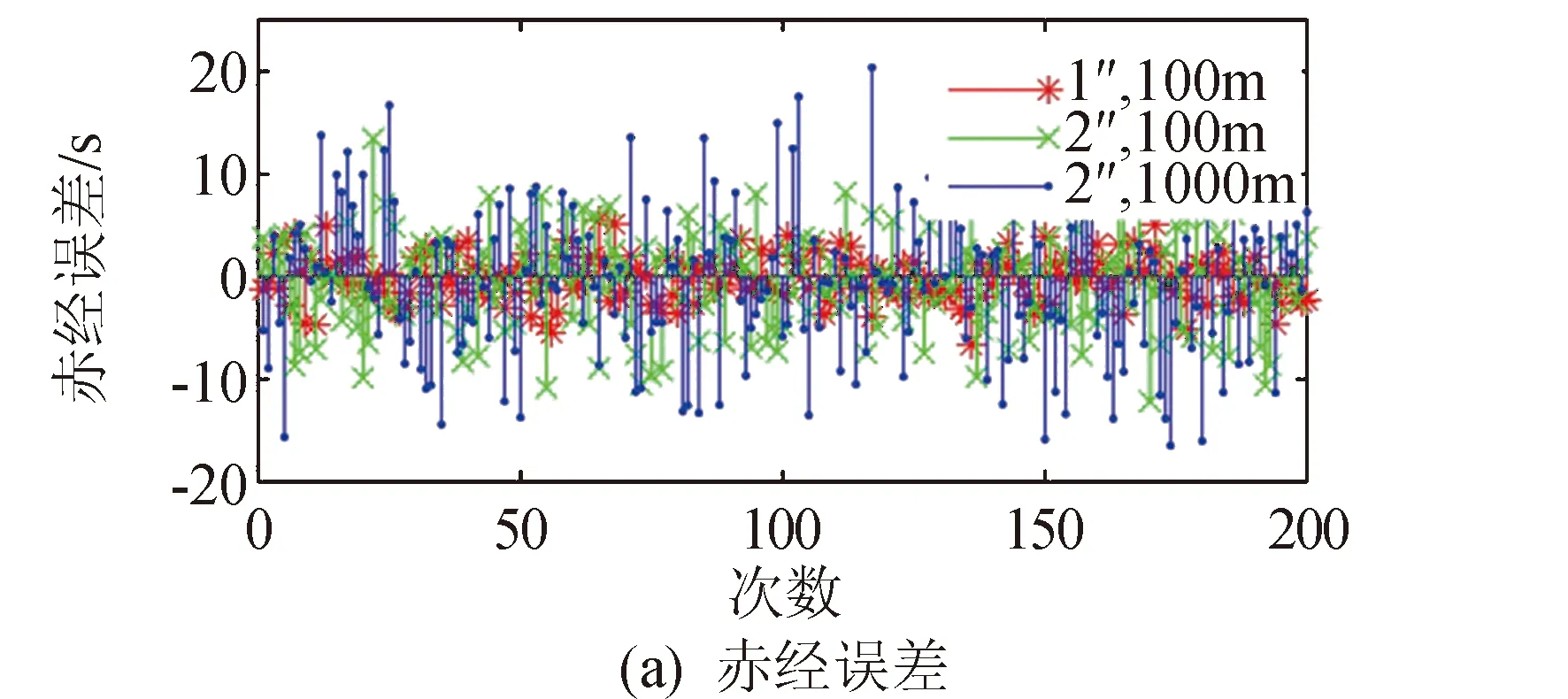
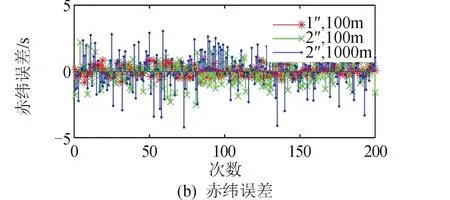
圖9 多星敏感器協同觀測赤經赤緯定位誤差Fig.9 Right ascension and declination positioning error under multi-star sensor

3.2 空間目標短弧關聯仿真

仿真中的空間目標數據來自于美國優思科學家聯盟對在軌航天器的實測數據。仿真中加入3組噪聲水平，分別為(1″,100 m)，(2″,100 m)，(2″,1 000 m)。新舊航跡的間隔時間為1～10 h，每組噪聲下進行200次關聯仿真。為了驗證短弧關聯效果，新舊航跡段的觀測時長均不超過2 min，最短航跡為50 s。關聯結果有4種可能，即正確關聯相關目標、正確拒絕不相關目標、錯誤關聯不相關目標、錯誤拒絕相關目標，其中前兩者屬于正確關聯，統計仿真中算法的正確率。

當待關聯對象為GEO目標時，由于赤緯的變換范圍極小，以擬合的殘差平方和判斷航跡相關與否區分度不明顯，因此仿真中對赤緯數據統一放大1 000倍，可以區分軌道傾角相差0.01°的空間目標。由式(9),對于一個GEO目標，運動時長T后，其位置的不確定范圍為以它真實位置為圓心，50 km/h×T為半徑的球。因此當間隔時長T≤12 h時，T越大空間目標的不確定范圍越大，因此關聯的準確率會隨間隔時間下降。噪聲條件下的關聯準確率如圖10所示，由圖可知，當新舊航跡間隔3 h時，3種噪聲條件下，關聯準確率均達到90%以上，而目標被星敏感器觀測的間隔時間一般小于2 h，因此本文算法可以適用于星敏感器下空間目標的航跡段關聯。

仿真中發現，關聯準確率與殘差平方和的門限值有關，當門限值取得過小會導致錯誤的拒絕相關目標，門限值取得過大則可能導致錯誤的關聯不相關目標。根據仿真，若一段航跡采樣點數為N，關聯準確率最大的門限值ε取值范圍為[0.2N，0.75N]，本文關聯門限取0.25N。

圖11為仿真中兩條舊航跡與新航跡集合的擬合關聯過程。圖11(b)中舊航跡與兩條新航跡的正弦擬合殘差平方和均在閾值范圍內，依據式(11)(12)的約束，最終將新舊航跡正確關聯。

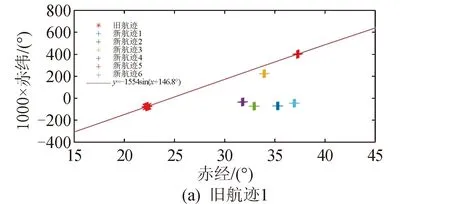
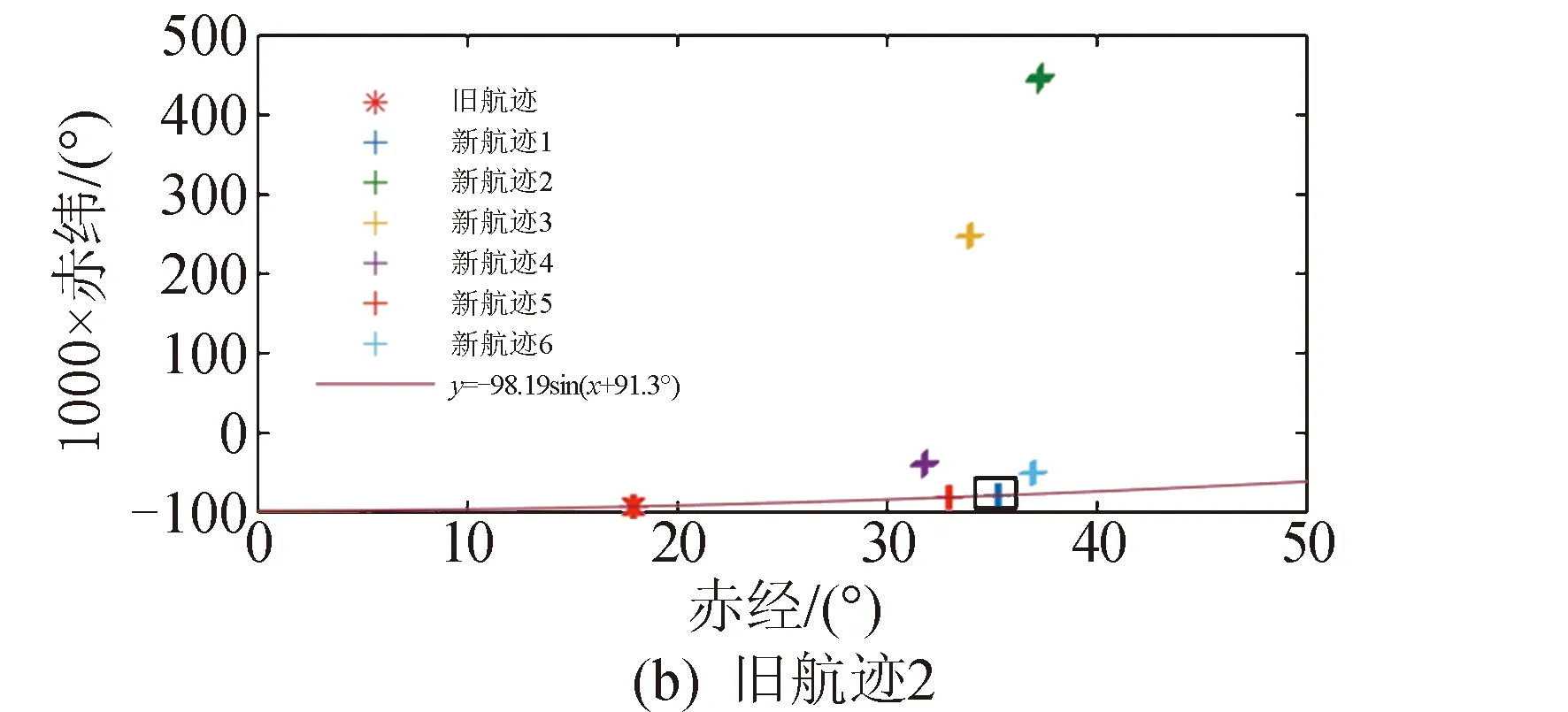
圖11 舊航跡與新航跡的擬合關聯過程Fig.11 Fitting process between old track and new track

將本文算法與基于容許域和基于模糊關聯的航跡段關聯算法進行對比。噪聲選擇為更接近工程實際的(2″，100 m)，擬合關聯門限取0.25N。如表2所示，可以看出本文算法的優勢是運算快，無需定軌，可以適用于短間隔、快速響應的任務需求。隨著未來星間鏈路[19]、星地鏈路的建設[20]及空間信息網絡[21]的發展，快速響應算法有助于星上即時關聯的實現，本文算法的局限性是需保證協同觀測的傳感器數量至少為2臺。

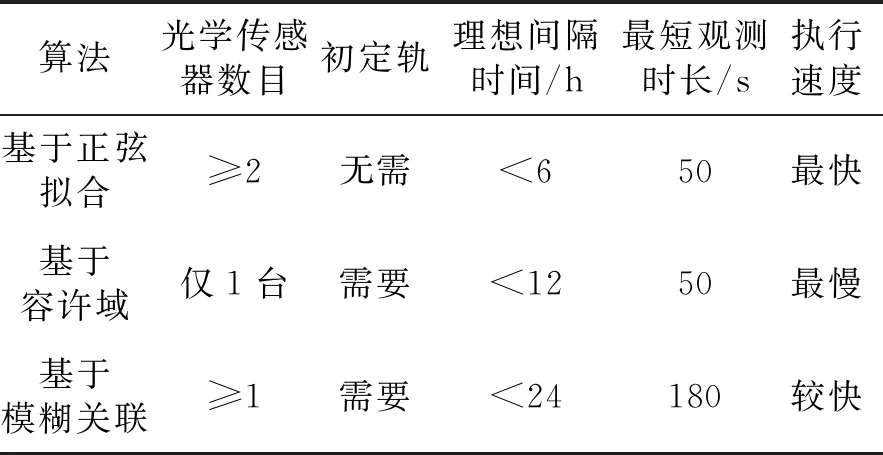
表2 中斷航跡關聯算法對比

4 結束語

本文應用多星敏感器下空間目標同步關聯結果計算空間目標位置。在仿真噪聲條件下，赤經赤緯誤差為角秒級，其中星敏感器自身位置誤差的標準差為100 m，測角誤差的標準差為2″時更接近工程實際中的噪聲水平。在此噪聲水平下，空間目標赤經誤差的標準差為4.94″，赤緯誤差的標準差為0.93″，可以滿足后續關聯的精度需求。

通過將空間目標赤經、赤緯進行正弦擬合，可以較好地區分軌道傾角不同的軌道，采用余弦擬合效果相同，但是對于處于相同軌道但相位不同的空間目標或僅軌道高度不同的目標缺乏區分能力。因此若目標關聯對象為GEO目標時，需要根據GEO目標運動規律加入半長軸以及運動角速度約束。

本文算法無需進行初始軌道確定，是一種簡便快捷的短弧關聯算法。本文最短關聯50 s的觀測短弧，當觀測弧段更長時方法依然適用，且關聯準確率更高。本文算法更適用于間隔時間小于3 h的航跡段關聯場景，當新舊航跡間隔3 h時，本文3組噪聲水平下的關聯準確率均達到90%以上。