磁流變阻尼器參數化模型的研究綜述

陶 柯 免

(同濟大學土木工程學院，上海 200092)

1 概述

磁流變阻尼器(magnetorheological damper，MRD)因其結構簡單、動態范圍寬、響應速度快、阻尼力大且連續順逆可調等優點[1,2]，在結構振動控制中有廣泛的應用前景。為了充分發揮磁流變阻尼器良好的性能，必須建立精確且簡單實用的力學模型，以保證控制算法的實時有效，從而達到對結構的精準控制。由于磁流變液的黏性特征以及外加磁場等導致MRD的非線性滯回特性，增加了建立力學模型的難度，國內外學者做了大量工作，提出了多種MRD模型，主要分為參數化和非參數化模型[3]。

參數化模型大多基于磁流變阻尼器的動力性能測試試驗，從試驗中可以得到磁流變阻尼器的阻尼力—位移曲線和阻尼力—速度曲線，通過預設理論表達式，進行曲線擬合，然后不斷調整參數，最終確定阻尼器出力的數學表達式。比較常見的磁流變阻尼器參數化模型有Bingham模型[4]、非線性雙粘性滯回模型[5]、Bouc-Wen模型[6]等；非參數化模型基于磁流變阻尼器動力性能測試試驗數據，采用神經網絡等智能算法來建模。本文分析了幾種主要的參數化模型以及其改進型的優缺點，并對發展方向進行了闡述。

2 MRD參數化模型及其改進型

2.1 Bingham模型及其改進型

2.1.1Bingham黏塑性模型

Stanway等[7]基于電流變體的Bingham偽靜力模型，提出了理想化的MRD模型，隨后，Spencer等將該模型引入到MRD的動力學模型中。其力學模型由一個黏滯阻尼元件和一個庫侖摩擦元件并聯組成，該模型假定磁流變液屈服前為剛體且不流動，屈服后才開始流動且為非零屈服力的牛頓流體。其阻尼力的表達式為:

(1)

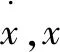
Bingham模型簡單，能較準確地反映阻尼力—位移關系，但對低速區的阻尼力—速度關系卻誤差較大。這是因為該模型忽略了磁流變液黏彈體的本構關系。

2.1.2Bingham模型的改進型

Bingham模型雖然不能很好地描述MRD的阻尼力—速度的滯回關系，但因結構簡單、概念明確，在研究初期還是得到了一些推廣。

周強等[8]根據阻尼特性試驗結果，將Bingham單元與一個彈性元件串聯，提出了修正的Bingham模型，能較好地模擬阻尼力—位移關系，但是黏塑性單元的位移難以確定，應用較少；Occhiuzzi等[9]提出黏滯阻尼和控制電流成線性關系，將式(1)中的速度項重新描述，提出了擴展的Bingham模型，結果可以較好地描述阻尼力—速度曲線的非線性特性，但是仍然不能擬合阻尼力—速度曲線的滯回特性。

2.2 非線性滯回雙黏性模型及其改進型

2.2.1非線性滯回雙黏性模型

滯回特性是MRD的一個很重要的特征。由于Bingham模型及其改進型均不能體現滯回特性，Wereley等[5]在非線性雙黏性模型[10]的基礎上，提出了非線性滯回雙黏性模型。不同于Bingham模型基于磁流變液屈服前為剛性的假定，該模型假設磁流變液屈服前后都是塑性，用6個分段函數來表示阻尼力，其表達式為：

(2)

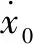
該模型基本能描述阻尼力—位移和阻尼力—速度曲線的非線性特征，使用分段函數能一定程度上反映MRD的滯回特性，但是引入的減速、加速屈服速度值隨控制電流、激勵的變化而變化，且得不到解決，難以應用到控制領域。

2.2.2非線性滯回雙黏性模型改進型

為了改進非線性滯回線性模型的滯回曲線光滑性問題，薛建海等[11]基于式(2)，將分段阻尼力曲線簡化為直線和正弦曲線組成的四段非線性函數曲線，提出了非線性滯回反正切模型，提高了MRD滯回曲線的光滑度，但是模型的復雜度和參數的確定問題并沒有得到解決。

2.3 Bouc-Wen模型及其改進型

2.3.1Bouc-Wen模型

非線性滯回雙黏性模型分段不連續，難以描述阻尼力—速度關系，Bouc提出了一種光滑的遲滯模型，此后Wen加以發展和完善，提出了Bouc-Wen模型[6]，其表達式為：

(3)

(4)

其中，α由控制系統和磁流變液決定；z為滯變位移；c0為MRD運動速度較大時的黏滯阻尼系數；k0為剛度系數，MRD阻尼力—速度的光滑性決定γ,β和A，以上均為常數。

該模型較Bingham模型能更準確地反映MRD低速時的非線性能力，且計算方便、通用性好，已在滯回系統建模中得到廣泛應用。

2.3.2Bouc-Wen模型及其改進型

Yi等[12]針對剪切式MRD，在Bouc-Wen模型的基礎上提出了修正的Bouc-Wen模型，該模型去除了Bouc-Wen模型中的線性彈簧部分，且用Bouc-Wen滯回力模擬大應變時磁流變液的庫侖特性和低應變下粘彈性所表現出的復雜非線性特征。該模型簡單，但是用線性關系描述電流的非線性控制影響模型精度。Spencer等[13]提出了基于Bouc-Wen模型的現象學模型，能很好地描述MRD的動態響應，且能與各速度區的實驗數據相吻合，靈活性好。但是由于具有10多個待定參數，數據處理困難，在應用優化算法確定參數時容易發散。Bai等[14]引入歸一化概念對現象學模型進行了簡化，提出了變換現象學模型，有效地減少了模型參數的數量，簡化了模型，更精確地描述MRD的非線性滯回性能。

2.4 其他模型

除上述模型以外，很多學者也提出了其他參數化動力學模型。周強和瞿偉廉[8]根據磁流變阻尼器力學性能試驗結果，提出了修正的Dahl模型。該模型釆用Dahl模型模擬庫侖摩擦力，相對于Bouc-Wen模型，減少了待辨識參數的個數。徐趙東等[15]提出了帶質量元素的溫度唯象模型，該模型能模擬阻尼器的非線性滯回性能，同時能反映溫升效應對磁流變阻尼器的影響，但該模型需要解微分方程，計算速度慢。李秀領等[16]提出的雙Sigmoid模型能較準確地描述磁流變阻尼器的非線性滯回性能，但不能反映位移、頻率對磁流變阻尼器的影響。Chae[17]提出了Maxwell非線性滑移模型(MNS)，將磁流變阻尼器的動力學行為分成屈服前和屈服后兩部分進行單獨分析，并運用粒子群算法進行了模型參數識別，該模型參數少，物理意義明確，魯棒性好，能夠比較精確地描述磁流變阻尼器的動力學行為，而且在運用到實際結構控制中也能達到預期的控制效果。張香成等[18]通過對磁流變阻尼器進行力學性能試驗，并基于米氏方程提出一個綜合考慮電流、位移和頻率影響的米氏模型，該模型能較好地模擬阻尼力—位移曲線和阻尼力—速度曲線，而且能較好地描述阻尼力—速度曲線低速時的非線性滯回性能，并能反映位移、頻率對阻尼力—速度曲線滯回區域的寬度的影響。

3 MRD力學模型研究中存在的問題

由于目前對于磁流變液的微觀機理認識不足，前述國內外學者對MRD進行力學建模多數僅考慮阻尼器本身參數以及磁流變液種類、結構尺寸、荷載和環境等因素。這使得通過某種型號的MRD在一定工況下進行有限次實驗結果進行參數擬合得到的參數化模型，均存在各自缺陷，且魯棒性均不甚理想。如：Bingham模型及其改進型雖然簡單，但是難以描述阻尼力—速度關系；非線性滯回雙粘滯模型不光滑；Bouc-Wen模型及其改進型雖然能夠較準確地模擬阻尼力的動力特性，但待定系數過多，求解過程過于復雜。

鑒于參數化模型的諸多缺點，近年來以神經網絡為代表的非參數化模型發展迅猛。Chang等[19]采用神經網絡來模擬磁流變阻尼器的非線性動力特性，分別建立了所研究阻尼器的正向和逆向動力學模型，可用于工程結構的在線控制。廖英英等[20]采用遺傳算法和BP神經網絡結合，建立了MRD的逆向模型并應用于1/4車半主動懸掛系統，數值仿真結果證明其建立的模型可以較好地預測控制電流。周勇等[21]提出了一種網絡連接權值自適應調整的改進RBF神經網絡，有效地降低了模型的誤差，能滿足工程需要。相比于參數化模型，這些非參數化模型具有更好的泛化能力與魯棒性。

4 結語

MRD參數化模型種類多樣，且部分能很精確地模擬阻尼器的動態特性，應用廣泛，但由于模型建立多是針對固定工況，難以直接反映阻尼器的逆向動態特性。相比之下，基于神經網絡和模糊邏輯的非參數化模型不但能更好地描述MRD的滯回特性，也能更準確地建立逆模型，在半主動控制中有更廣泛地應用。