現代資產組合理論在中國A股市場的有效性研究

李偉

摘要：現代資產組合理論是金融投資最為經典的理論之一，馬科維茨投資組合模型作為投資學的重要理論模型，為投資者提供了科學的資產配置方法，目前在國際上得到了廣泛的應用和研究。現代資產組合理論通過對資產的歷史收益率進行統計分析，來指導未來一段時間的投資行為。但是，我國理論界和實務界對于該理論本身的缺陷以及是否適用于中國A股市場一直存在較大爭議。本文隨機選取了中國A股市場中的4支股票，根據此理論構建了最大夏普比率權重、市值權重以及平均權重三種策略組合，通過績效評價指標對幾種策略組合的績效進行比較，以驗證馬科維茨資產組合理論在中國A股市場的適用程度。

關鍵詞：資產組合理論? 馬科維茨投資組合模型? A股市場? 投資組合業績評價

一、前言

隨著我國金融體系的逐步建立和完善，人們的投資方式越來越多樣化，為了分散和降低投資風險，組合型投資成為比較理想的理財方式，受到越來越多的重視。在配置資產組合時，如何衡量資產的風險和收益，如何將財富在多種資產中合理分配成為重要問題。美國經濟學家哈里·馬科維茨首次將風險和收益進行了量化，建立了均值方差模型，是確定最佳資產組合的基本模型[1]，均值-方差模型作為現代資產組合理論中的經典，在1952年由美國經濟學家哈里·馬科維茨提出，其后又在威廉·夏普、斯蒂芬·羅斯等人的深化下衍生為資本資產定價、套利定理等理論，是現代金融學的核心研究方向之一[2]。現代投資組合理論也從這開始發展，該理論推動了當前資產管理業務趨向組合化、科學化，如何構建組合一直是現代投資組合理論的研究熱點。中國學者曾穎苗等（2009）用VaR代替方差作為風險度量指標建立了均值-VaR投資組合模型，認為中國證券市場中均值-方差策略優于等權組合策略[3]。學者李金鑫（2014）等則認為等權組合策略在中國證券市場的表現在統計方面要好于均值-方差策略[4]。美國學者Frankfurter[5]等認為在美國證券市場市值加權策略更為有效，不同策略在不同環境的市場中表現不同。在已有的研究基礎上，本文隨機選取了我國A股市場中的4支股票，根據理論構建了最大夏普比率權重、市值權重以及平均權重三種策略組合，通過績效評估指標對幾種策略組合的績效進行分析，比較各種策略的優劣，以驗證馬科維茨投資組合模型在中國A股市場是否具有有效性。

二、馬科維茨投資組合模型

1952年，馬科維茨在《資產選擇：有效的多樣化》一文中，將邊際分析原理運用于資產組合的分析研究。運用資產組合報酬的均值和方差這兩個數學概念作為投資組合收益和風險的無偏估計，從數學上明確地定義了投資者偏好。馬科維茨模型的假設條件：

一是投資者在考慮每一次投資選擇時，其依據是某一持倉時間內的證券收益的概率分布。

二是投資者是根據證券的期望收益率估測證券組合的風險。

三是投資者的決定僅僅是依據證券的風險和收益。

四是在一定的風險水平上，投資者期望收益最大;相對應的是在一定的收益水平上，投資者希望風險最小。

根據以上假設，馬科維茨確立了證券組合預期收益、風險的計算方法和有效邊界理論。建立了資產優化配置的均值-方差模型：

其中rp為組合收益，ri為第i只股票的收益，xi、xj為證券 i、j的投資比例，б2（rp）為組合投資方差，Cov（ri，rj）為兩個證券之間的協方差。上式表明，在限制條件以及一定的組合期望收益率下，可通過拉格朗日目標函數求解Xi 證券投資比例使得組合的風險б2（rp）最小。馬科維茨的投資組合理論不僅揭示了資產組合的風險決定因素，而且還揭示了“資產的期望收益由其自身的風險的大小來決定”這一重要結論。即資產由其風險大小來定價，單個資產的風險由其方差或標準差來決定，組合資產的風險價格由其協方差來決定。以組合收益率標準差和期望值作為橫、縱坐標軸，模型的可行解集為一條凹向原點的邊界曲線，曲線的上半部分被稱為有效邊界，如圖1。

有效邊界圖形揭示出：單個資產或組合資產的期望收益率由風險測度指標標準差來決定。風險越大收益率越高，風險越小收益率越低。其經濟學意義是：投資者可預先確定一個期望收益，通過計算可確定投資者在每個投資項目（如股票）上的投資比例（項目資金分配），使其總投資風險最小。

引入無風險資產后，資本可以在無風險資產與證券市場間自由分配，新組合收益與風險的線性關系叫做資本配置線（CAL）：

其中r f為無風險收益率，E（rM）為引入無風險資產后的資本市場組合的期望收益率，бM 為市場組合風險，資本配置線的斜率[E（r p）-r f]/σp 也被稱作夏普比率，夏普比率的大小表明風險資產每承擔一單位的風險能夠獲得多少超額收益，夏普比率越大，表明風險補償越高，投資組合的性價比越高。當資本配置線的斜率與有效前沿相切時，資產組合的夏普比率達到最大，切點為資產組合有效前沿上的最優資本配置點，資本配置市場有效且達到均衡，如圖2，所有有效組合是不同風險偏好的投資者在無風險資產與市場組合間自由分配的結果。

三、不同組合策略在中國A股市場的實證研究

（一）個股選擇

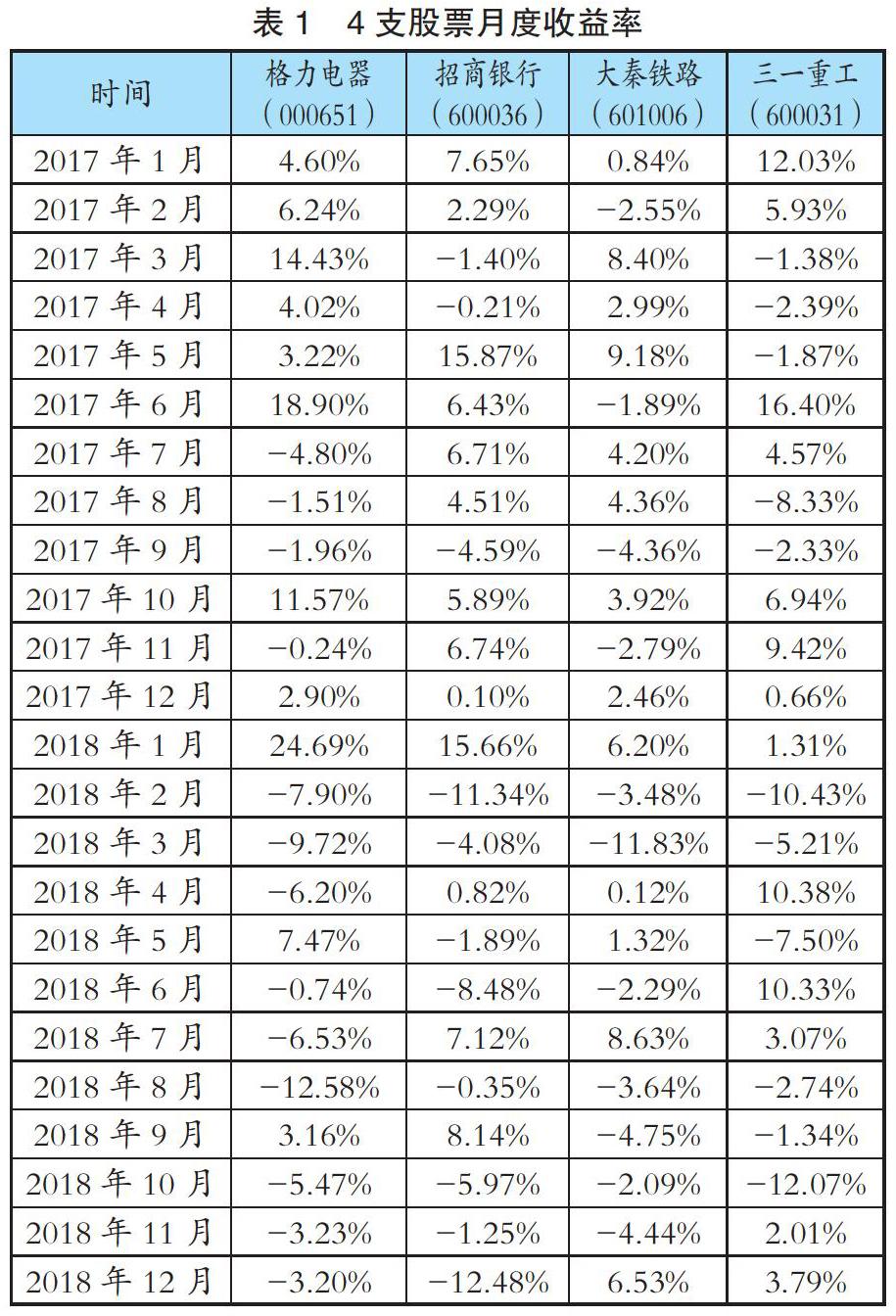
為研究資產組合理論在中國A股市場上的實用性，本文將從中國滬深市場不同行業隨機抽取4支股票運用不同策略構建資產組合。個股市值權重、平均權重是常用的資產配置策略，鑒于國內不同學者對不同策略的效果持有不同的觀點，本文同時用最大夏普比率權重、市值權重以及平均權重三個策略構建資產組合，最后通過業績評價的方式對其進行評述。以每支股票2017年、2018年兩年的月度收益率作為歷史數據，用于估計股票的預期收益率和標準差，用三種組合2019年的月度收益率對不同策略組合的效果進行檢驗。隨機選取了4支股票數據并計算了月度對數收益率見表1。

（二）數據處理并構建組合

1.計算4支股票月度收益率的均值和標準差見表2。

2.計算4支股票月度收益率的協方差矩陣見表3。

3.引入無風險收益率。本文將引入一年期定期存款利率1.5%作為無風險收益率，轉換為月度無風險收益即為0.125%。根據馬科維茨資產組合理論，組合的夏普比率=（組合收益率均值-無風險收益率）/組合標準差。我國實行“T +1”證券交易制度，并且在市場中做空證券的成本較高，因此研究賣空限制的投資組合模型更符合我國A股的實際情形。此時，賣空限制的資產組合模型中個股的權重非負，即∑xi=1且 xi≥0（不允許賣空）。利用數據處理軟件的規劃求解功能可得到當組合的夏普比率最大時的個股權重見表4，根據馬科維茨資產組合理論，按照夏普比率最大時的權重構建的組合將是資產組合有效前沿上的最優資本配置點所代表的資產組合。

4.根據市值權重策略和平均權重策略構建組合，見表5。其中個股市值取2018年最后一個交易日即2018年12月28日的數據。

（三）投資組合績效評價

根據2019年度4支股票的數據計算各組合的月度收益率，并引入同期滬深300的月度收益率數據作為市場參照指標，見表6。

根據2019年度三種組合的月度收益率可得到各組合的回測情況見表7。從產生的收益上看，這三個組合的年化收益率和月度收益率均值均跑贏了滬深 300 基準指數，且月度收益率標準差都小于同期滬深300的收益率標準差，說明通過組合投資能夠在短時間內規避一定的市場風險，獲得較好的收益。從以收益率標準差衡量的風險角度評價，等值權重組合無疑是風險最小的組合，且等值權重組合的收益率高于市值權重組合，綜合結果表明等值權重組合優于市值權重組合。夏普組合雖然收益率標準差較高，但是在收益率均值、夏普比率和年度收益率方面對其他兩個組合都有一定的優勢，表明夏普組合每承擔一單位風險獲得了相對于其他組合更高的單位收益并且最終獲得了更高的絕對收益，所以最大夏普比率組合策略是一種有效的投資策略。

四、總結

馬科維茨資產組合理論認為，若干種風險資產組成的投資組合，其收益是這些風險資產收益的加權平均數，但是組合的風險并不是這些風險資產的加權平均風險，投資組合能降低非系統性風險，組合資產的期望收益率由風險測度指標標準差來決定。風險越大收益率越高，風險越小收益率越低。歷史收益率的均值和方差可以作為組合的收益率和方差的無偏估計。通過計算最大夏普比率，可以得到風險收益均衡下的最優風險資產組合權重。本文收集了A股市場4支股票的歷史數據，根據理論構建了最大夏普比率組合、市值權重組合以及平均權重組合，并對三個組合在一定期間內的表現進行了分析評價。三個資產組合在期間收益和風險兩個方面都跑贏了滬深300基準指數，說明通過組合投資能夠在短時間內規避一定的市場風險，獲得較好的收益。最大夏普比率組合相對其他兩個組合在收益率均值、夏普比率和年度收益率方面都有一定的優勢，說明最大夏普比率組合策略是一種有效的投資策略，馬科維茨投資組合理論對我國A股市場的投資有一定的實踐指導意義。但是馬科維茨投資組合模型對資產收益率的分布進行了比較嚴密的假設，完全按照資產的歷史收益率的均值和方差進行投資組合的資產配置也有一定的局限性，由于均值和方差在估計過程中的誤差以及宏觀經濟形勢的變動，投資者在實際的投資活動中，實際組合的收益率均值和方差與歷史數據存在較大的差異，最終的投資很難達到理想的結果。本文的不足之處在于：一方面構建投資組合的標的數量較少，回測結果具有一定的偶然性;另一方面對于回測結果的分析比較簡單，評價指標不夠豐富，運用馬科維茨投資組合理論構建的最大夏普比率組合的優勢并不明顯。

參考文獻：

[1]吳輝.時變金融市場下動態投資組合選擇理論及其應用研究[D].長沙：湖南大學，2016.

[2]Markowitz H.Portfolio Selection.Theory & Practice of Investment Management：Asset Allocation Valuation Port- folio Construction & Strategies Second Edition[M].New jersey：John Wiley & Sons Inc，2011.

[3]曾穎苗，張珺，張晴.馬科維茨模型在股市最優投資組合選擇中的實證研究[J].湘潭師范學院學報：社會科學版，2009，31（4）：88 -91.

[4]李金鑫，涂巍，王治國，等.最優資產配置模型適用于中國股票市場嗎[J].當代經濟科學，2014，36（2）：52-61.

[5]Frankfurter G M，Phillips H E，Seagle J P.Portfolio Selection：The Effects of Uncertain Means，Variances，andCovariances[J].Journal of Financial& Quantitative Analysis，1971，6（5）：1251 -1262.

作者單位：安徽大學經濟學院