應力回復對PVC膜材應力松弛行為的影響

汪澤幸，吳 波，朱文佳，何 斌，劉 超

(1. 湖南工程學院 紡織服裝學院，湖南 湘潭 411104;2. 湖南省新型纖維面料及加工工程技術研究中心，湖南 益陽 413000)

膜材通常以聚酯纖維或玻璃纖維織物為增強體，以聚氯乙烯(polyvinyl chloride，PVC)、聚四氟乙烯(polytetrafluoroethylene，PTFE)、聚偏氟乙烯(polyvinylidene fluoride，PVDF)等為基體，采用涂層加工方式制備而成[1-2]。作為一種具有明顯非彈性、非線性、黏彈性且具有正交各向異性特征的柔性復合材料，其黏彈性以蠕變和應力松弛的形式展現(xiàn)出來。應力松弛過程中，因材料內部結構的調整，導致材料內部的應力持續(xù)降低，雖應力松弛不會引起膜材的宏觀破壞，但會導致膜結構表面整體剛度降低，在強風作用下引起膜結構表面出現(xiàn)大幅度的反復擺動，最終引起膜材的撕裂破壞[3]。為避免使用過程中膜結構表面的張力過度損失，需定期進行張力檢測，并根據需要對膜結構表面的張力進行調整。

膜材作為一種具有顯著黏彈特性的工程材料，其力學行為不僅與所受的應力狀態(tài)相關，還與加載歷史密切相關。為全面研究以膜材為代表的織物增強類柔性復合材料的應力松弛行為，眾多學者對PVC膜材[4-8]、PTFE膜材[7, 9-11]及其他涂層織物類柔性復合材料[12-13]在不同條件下的應力松弛行為及其描述模型進行了研究，但這些均在應力松弛前無應變或應力回復歷史條件下進行。

現(xiàn)有研究表明，高聚物[14-16]、纖維[17-18]、紗線[19-23]、織物[23-24]、復合材料[25]等具有回復滯后的材料，應力松弛前如有應變或應力回復歷史，應力松弛過程中試樣中的應力將呈非持續(xù)衰減趨勢，即表現(xiàn)為非尋常的應力松弛行為。根據應力與松弛時間之間的變化規(guī)律，將應力松弛行為可分為3類[26]，即簡單應力松弛行為、混合應力松弛行為與逆應力松弛行為。文獻[22]認為醋酸長絲和滌綸長絲的應力松弛行為可采用基于多個Maxwell單元串聯(lián)的廣義元件模型來描述，但未對模型合理性進行驗證。文獻[23-24]通過將1個定參數彈簧元件與2個定參數Maxwell單元并聯(lián)構建了5元件模型，闡述了逆應力松弛和混合應力松弛現(xiàn)象的產生機理，并對纖維、紗線等的逆應力松弛行為進行了擬合分析，但未驗證描述混合應力松弛和簡單應力松弛時的擬合精度。文獻[26-27]基于定參數彈簧和分數階導數元件構建了分層模型，該模型可較好地描述聚乙烯樹脂的簡單應力松弛行為，而對混合應力松弛與逆應力松弛行為的擬合效果較差。文獻[14-15]基于半結晶聚合物的黏彈性和黏塑性響應行為構建了兩相模型，該模型能較好地描述聚丙烯樹脂的簡單應力松弛、混合應力松弛及逆應力松弛行為，但由于本構方程含有復雜的積分項，計算過程繁瑣，使用不便。文獻[16]基于聚合物過應力模型對聚丙烯的短時混合應力松弛行為進行了模擬分析，但未對簡單應力松弛和逆應力松弛行為進行擬合分析。

基于此，為深入研究膜材在復雜受力歷史條件下的力學行為，以商購PVC膜材為研究對象，對其應力回復后的應力松弛行為進行測試和分析，基于非線性黏彈性元件建立雙變參數元件模型，并分析模型描述該膜材應力松弛行為的適宜性。

1 試驗材料與方法

以商購施恩特PVC膜材為試驗對象，其表層涂覆PVDF為耐氣候層，實測膜材厚度為0.72 mm。試樣為長300 mm、寬50 mm的矩形試樣，有效夾持隔距L0為200 mm，兩端夾持部位均采用高強黏合劑黏合不銹鋼薄片加以保護。

膜結構施工過程中，預加張力通常采用單位寬度內膜材上施加的載荷來表示，且在研究膜材的應力松弛行為時亦可在設定初始張力的條件下進行[4-5, 7, 9-11]，同時，為確保試驗過程中試樣始終處于拉伸狀態(tài)，本文采用應力控制方式對膜材的應力松弛行為進行測試。

試樣應力回復后的應力松弛代表性試驗過程如圖1所示。其中，OA曲線段，試樣以10 mm/min的拉伸速率v歷經時間t1(s)加載至最大應力σmax(N/mm)，然后以同等速率v歷經時間(t2-t1)卸載至初始松弛應力σ0(如AB曲線段所示)，保持σ0對應的應變ε0，保持時間t*(t*=t-t2)為14 400 s(如BC曲線段所示)。

圖1 代表性試驗過程曲線Fig.1 Representative total testing curve

所有試驗均在WDW-20C型微機控制電子試驗機上進行，環(huán)境溫度為25 ℃，有效試驗樣本數為3，以代表性應力松弛曲線為后續(xù)分析對象。

2 結果與討論

2.1 應力松弛行為分析

應力松弛前最大應力σmax為30 N/mm，不同初始松弛應力σ0時，膜材經、緯向試樣的應力松弛曲線如圖2所示。由圖2可知，觀測時間內，膜材經、緯向試樣均表現(xiàn)出3種形式的應力松弛行為：(1)當應力松弛前無應力回復歷史時，即應力回復量σ(σ=σmax-σ0)為0，膜材表現(xiàn)出簡單應力松弛行為，應力隨松弛時間的增加而持續(xù)減小；(2)應力回復量較大時，隨松弛時間的增加，應力呈逐漸增大的趨勢，即表現(xiàn)出明顯的逆應力松弛行為；(3)應力回復量較小時，隨松弛時間的增加，應力呈先增大后減小的趨勢，即表現(xiàn)出混合應力松弛行為。

(a) 經向

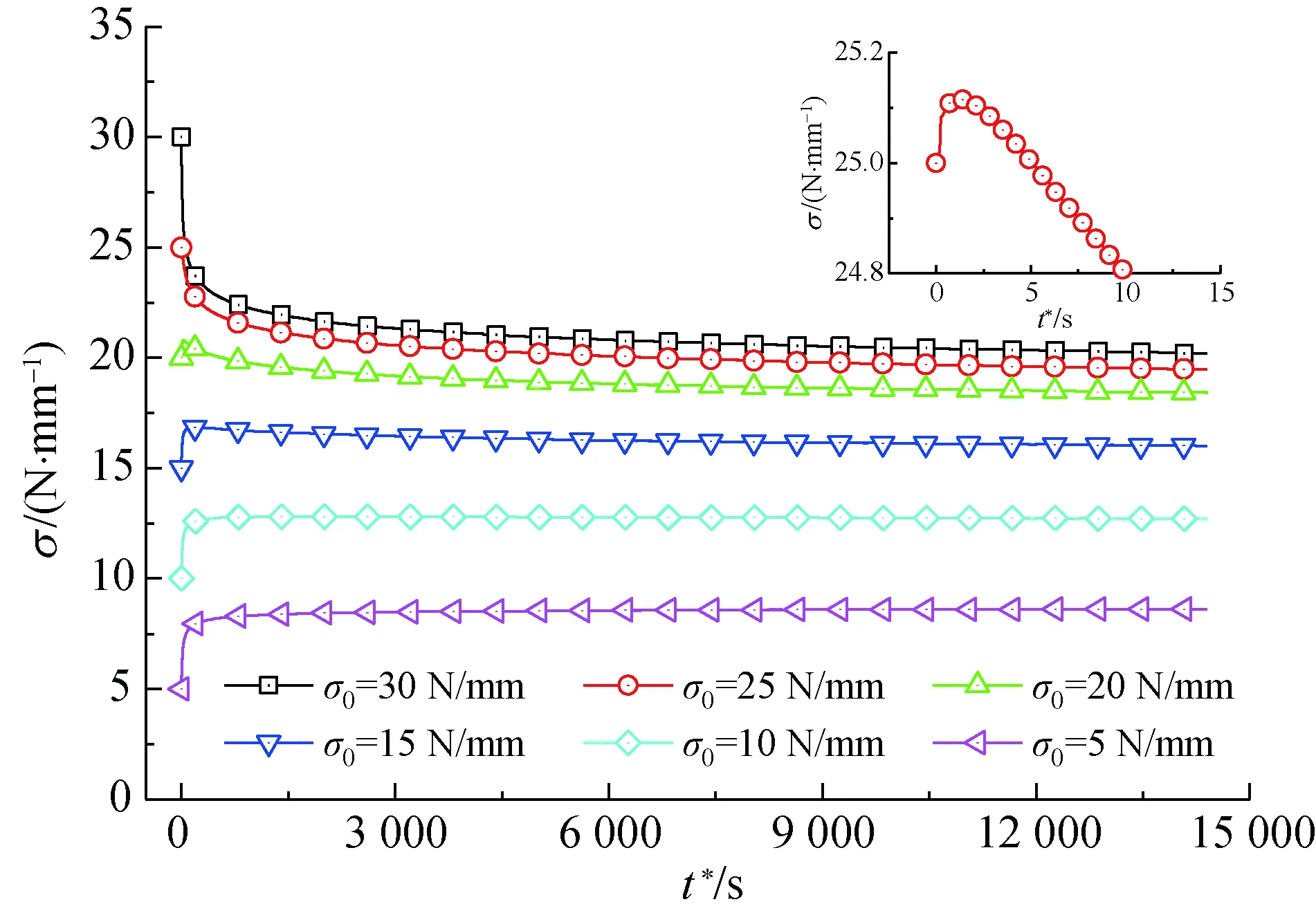
(b) 緯向

試樣處于等速拉伸階段(圖1中OA曲線段)時，隨著加載的進行，增強體纖維和表層涂覆材料的大分子鏈伸長，且與其他大分子鏈結合較弱的大分子鏈被拆散，此時產生相對滑移并在新的位置上建立連接，所有大分子鏈均處于拉伸狀態(tài)，且增強體纖維與涂覆高分子材料之間出現(xiàn)脫黏現(xiàn)象，從而產生不可逆的塑性變形。

應力松弛前無應力回復歷史時，松弛過程中增強體和涂覆層大分子鏈均處于拉伸狀態(tài)，大分子鏈通過鍵角與鍵長改變、分子鏈構象調整、分子鏈滑移與重排等方式實現(xiàn)大分子構型的平衡，材料內部殘余應力逐漸降低并趨于恒定，材料表現(xiàn)為簡單應力松弛行為。

當應力松弛前存在應力回復時，隨著外加應力的減少，原有拉伸狀態(tài)的大分子鏈在內應力作用下向內回縮。當外加應力回復至初始松弛應力時，控制初始松弛應力對應的應變，但此時增強體纖維和涂覆層高分子材料的大分子鏈變形并未停止，由于增強體纖維和涂覆層高分子的長鏈結構和大分子運動的逐步性，大分子鏈在受外力作用時與外力相適應的形變不可能在瞬間完成，大分子鏈向內收縮和重排運動將繼續(xù)進行，并通過大分子鏈構象和重排直至與對應保持應變相適應的平衡態(tài)，而達到此平衡態(tài)所需的時間與初始松弛應力對應應變狀態(tài)時大分子鏈間的作用力相關。在大分子鏈回縮過程中，拉伸階段產生相對滑移與未產生滑移大分子鏈承受的內應力不同，在回縮過程中回縮速率存在差異，產生相對滑移的大分子鏈將對未滑移大分子鏈的回縮運動產生阻礙作用，同時，大滑移量大分子鏈也將對小滑移量大分子鏈的回縮也將起到阻礙作用，延遲大分子的向內收縮和大分子的重排運動。當應力回復量較小時，大分子鏈之間的阻礙作用對大分子回縮影響較小，大分子鏈的構象和重排可短時間內達到平衡，之后再通過大分子鏈的鍵角與鍵長改變、分子鏈構象調整等實現(xiàn)內應力的逐步降低，大分子鏈整體呈先收縮后拉伸的變化過程，宏觀表現(xiàn)為材料內應力呈先增加后減小的變化趨勢，即混合應力松弛行為。隨著應力回復量的增加時，大分子鏈之間的阻礙作用對大分子回縮造成的影響程度逐漸增加，大分子鏈構象和重排達到平衡狀態(tài)所需的時間也逐漸增加，當應力回復量達到某一閾值時，大分子鏈將始終保持收縮狀態(tài)，宏觀表現(xiàn)為材料內應力呈現(xiàn)持續(xù)增加的變化趨勢，即逆應力松弛行為。

從圖2還可以看出，PVC膜材經、緯向試樣的應力松弛曲線的形態(tài)高度相似，表明PVC膜材經、緯向試樣的應力松弛機理一致。基于此，后續(xù)以經向試樣為研究對象，對其在初始松弛應力為5 N/ mm時，不同最大應力下的應力松弛行為進行測試，結果如圖3所示。

圖3 σ0為5 N/mm時經向試樣的應力松弛曲線Fig.3 Stress relaxation curves of warp specimens at σ0 of 5 N/mm

從圖3可以看出，同等初始松弛應力下，隨最大應力增加，即應力回復量的增加，經向試樣表現(xiàn)出簡單應力松弛、混合應力松弛與逆應力松弛行為。

由圖2(a)與圖3可知，PVC膜材經向試樣的應力松弛行為與松弛前應力回復階段的最大應力與初始松弛應力密切相關。這主要是由不同最大應力和初始松弛應力條件下，大分子之間作用力以及大分子回復滯后性存在差異所致。

由圖2和圖3可知，歷經不同應力回復歷史后的PVC膜材在應力松弛過程中，試樣中的應力均不同程度地偏離設定的初始松弛應力，即對初始松弛應力的保持能力存在差異。為研究應力松弛過程中材料對初始松弛應力的保持能力，引入應力變化量σ(t)，其可表示為

Δσ(t*)=σ(t*)-σ0

(1)

式中：σ(t)為應力松弛過程中試樣所承受的應力，N/ mm。

經向試樣的應力變化量曲線以半對數形式繪于圖4中。

從圖4可以看出，應力松弛前歷經應力回復后的試樣對初始松弛應力的保持能力明顯高于無應力回復試樣，且保持能力與應力松弛前最大應力σmax和初始松弛應力σ0的選用密切相關。當σmax=30 N/ mm，σ0=20 N/ mm時，對初始松弛應力的保持能力較好；當σ0=5 N/ mm，σmax=10 N/ mm時，經向試樣對初始松弛應力的保持能力較好。

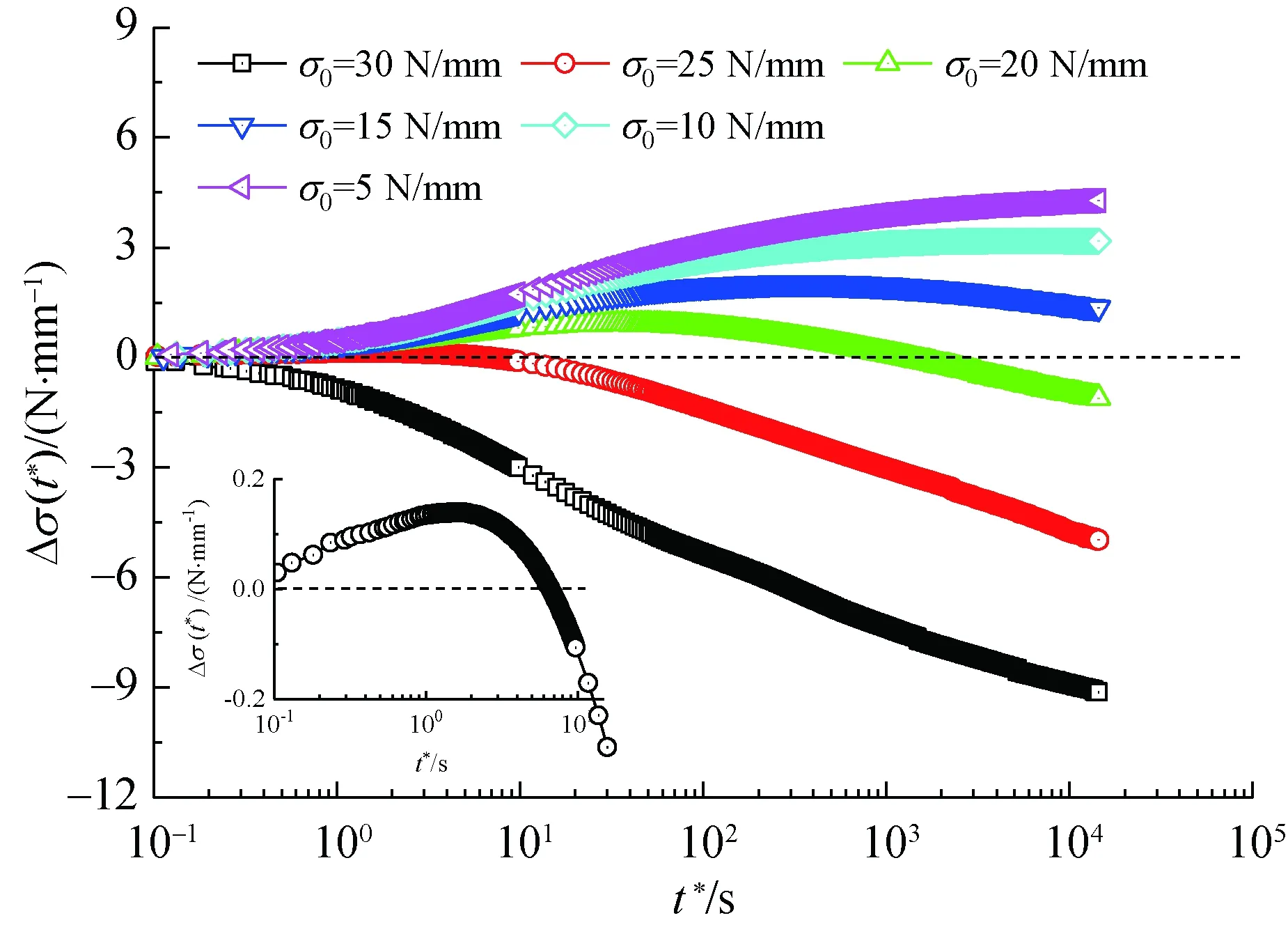
(a) σmax=30 N/ mm

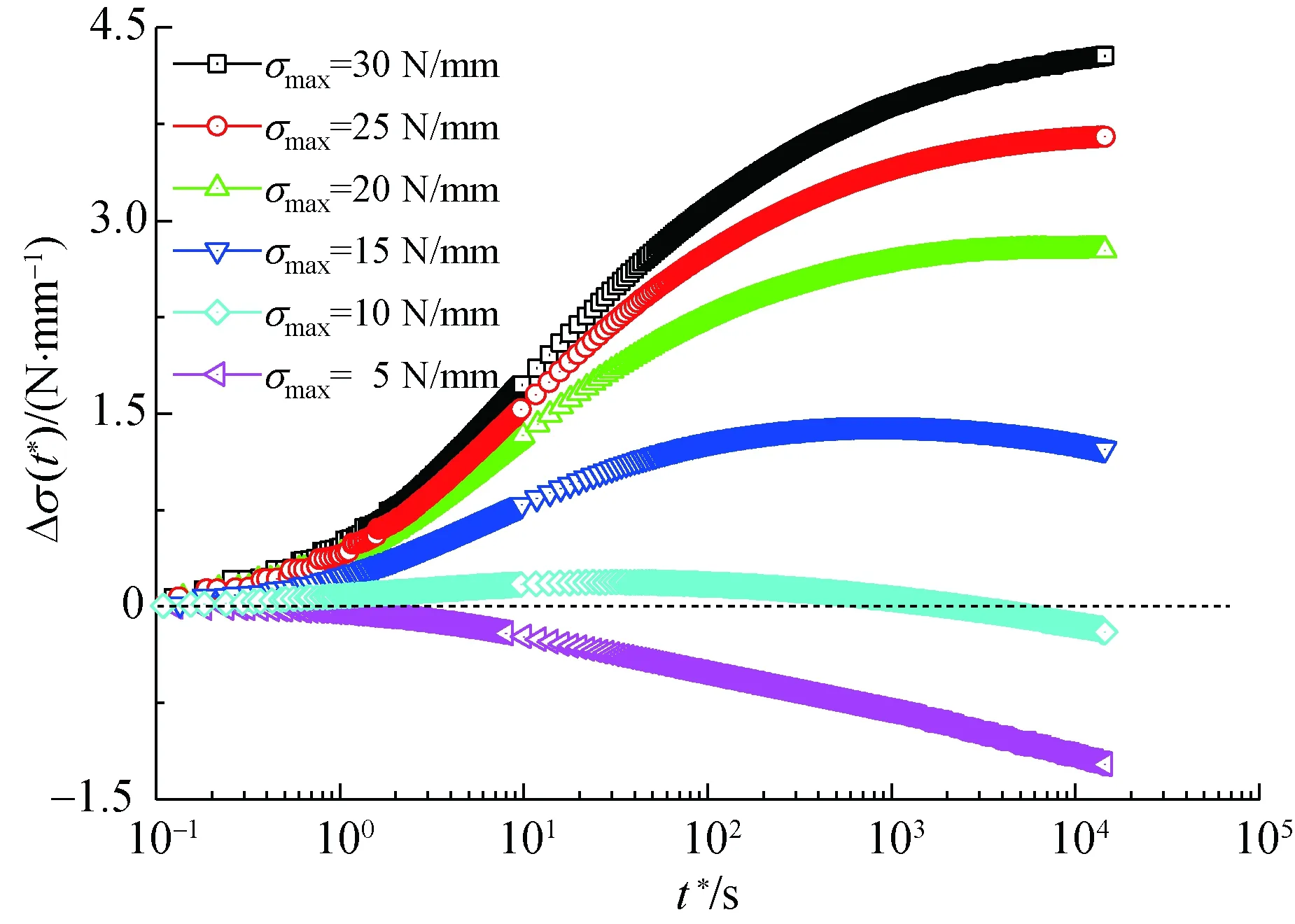
(b) σ0=5 N/ mm

從圖2可以看出，雖對膜結構表面施加較高的預加應力，可逐漸松弛到設計應力，但預加應力過大時，在外加載荷作用下膜材會提前進入塑性狀態(tài)，導致其承載能力降低。因而，對膜材施加的預加應力應小于膜材拉伸強度的5%(通常為1.5%～4.0%)[28]，并分步進行施加預加應力，在后期使用過程中定期檢測和反復調整。

基于此，利用歷經應力回復后PVC膜材對初始應力的保持能力高于無應力回復試樣的現(xiàn)象，在膜材施工過程中的膜結構表面預加應力施加階段，將膜材過度加載并卸載至設定的預加應力，可避免后期使用過程中膜面張力過度損失，從而在較長時間范圍內確保膜結構表面張力穩(wěn)定，延長膜結構表面張力調節(jié)的時間間隔，有效降低后期維護工作量。此外，該種方法需要使膜材短期加載至較高載荷并卸載，但相比直接施加較高載荷的方法，高載荷施加的時間較短，可避免膜材過早進入塑性階段，從而實現(xiàn)膜結構表面維持穩(wěn)定的目的。

2.2 定參數與變參數應力松弛模型

對Polciene等[22]建立的5元件模型(1個定參數彈簧與2個定參數Maxwell單元并聯(lián))中Maxwell單元數量進行拓展，獲得廣義Maxwell模型，如圖5所示。其中：E0、Ei分別為定參數彈簧元件和第i個Maxwell單元中彈簧的彈性模量，N/ mm；ηi為第i個Maxwell單元中黏壺的黏滯系數，N·min/ mm，i=1，2，… ，k。

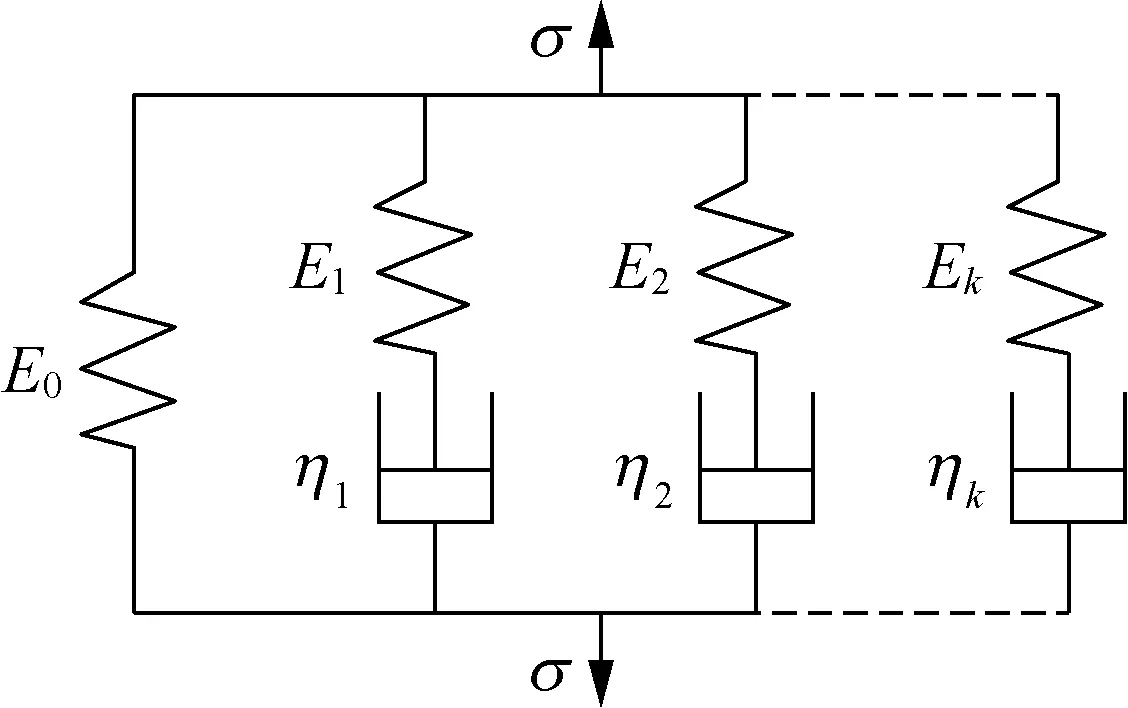
圖5 定參數元件模型Fig.5 Constant parameter element model

模型中第i個Maxwell單元的本構方程表達式σi(t)可表示為

(2)

當以速度v等速加載，試樣有效夾持長度為L0時，名義應變(t)可表示為

(3)

當模型應變以如式(3)所示的應變加載時，求解式(2)并考慮初始條件σi(t)|t=0=0，則第i個Maxwell單元的本構方程及其應力松弛σi(t*)的表達可表示為

(4)

(5)

式中：τi=ηi/Ei為第i個Maxwell單元的應力松弛時間，min；σ0i為第i個Maxwell單元的初始松弛應力，N/ mm。

應力松弛前，歷時t1加載至σmax且經過(t2-t1)后卸載至σ0時，第i個Maxwell單元的應力，即該單元的初始松弛應力σ0i可表示為[15]

(6)

圖5所示模型的應力松弛方程σ(t*)可表示為

(7)

該應力松弛表達式可簡化為

(8)

式中：A0=E0v(2t1-t2)/( 60L0) 。

(9)

式中：C0=A0-σ0。

上述模型由多個線性定參數彈簧和黏壺元件構建而成，同時，值得注意的是，在外加應力作用下，材料的微觀結構將發(fā)生變化，材料某些力學參數將隨時間的變化而發(fā)生變化，因而在構建元件模型時，需考慮元件參數的時間效應[29-30]。在構建非線性黏彈性元件建立變參數元件時，為便于計算，通常采用非線性黏滯體替代線性黏滯體，從而構建單變參數元件模型[4, 7, 9-11, 13, 30-34]。文獻[35-36]在單變參數元件模型的基礎上，基于元件的時間效應構建了雙變參數Maxwell模型，并認為黏壺元件黏滯系數η(t)和彈簧元件彈性模量E(t)隨時間變化的經驗函數[35]可表示為

η(t)=η0t1-n

(10)

E(t)=E0tm

(11)

式中：E0為非線性彈簧的初始彈性模量，N/mm；η0為非線性黏壺的初始黏滯系數，N·min/mm；n和m均為常數，00。

基于式(10)和(11)，建立的雙變參數廣義Maxwell模型的本構方程可表示為

(12)

求解上述方程組，可得松弛過程中應力增量的表達式為

(13)

式中：Di為式(13)中微分方程進行不定積分求解時的常數項。

2.3 模型擬合分析

基于圖4所示的應力變化量曲線，對上述兩種模型擬合效果進行分析，擬合結果如圖6和7所示。為避免過度定義未知參數而影響擬合效果，采用i=2廣義Maxwell模型的應力松弛簡化表達式對實測數據進行擬合分析。由于雙變參數廣義Maxwell模型的待定參數較多，故擬合參數初值需小心賦予，以避免出現(xiàn)擬合不收斂的現(xiàn)象。

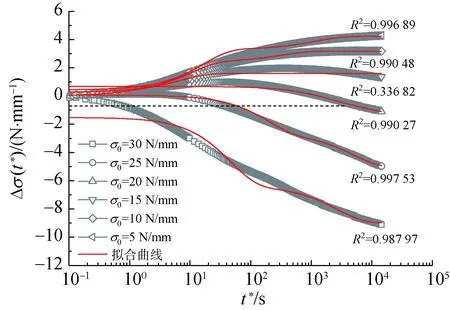
(a) 定常數廣義Maxwell模型

(b) 雙變參數廣義Maxwell模型

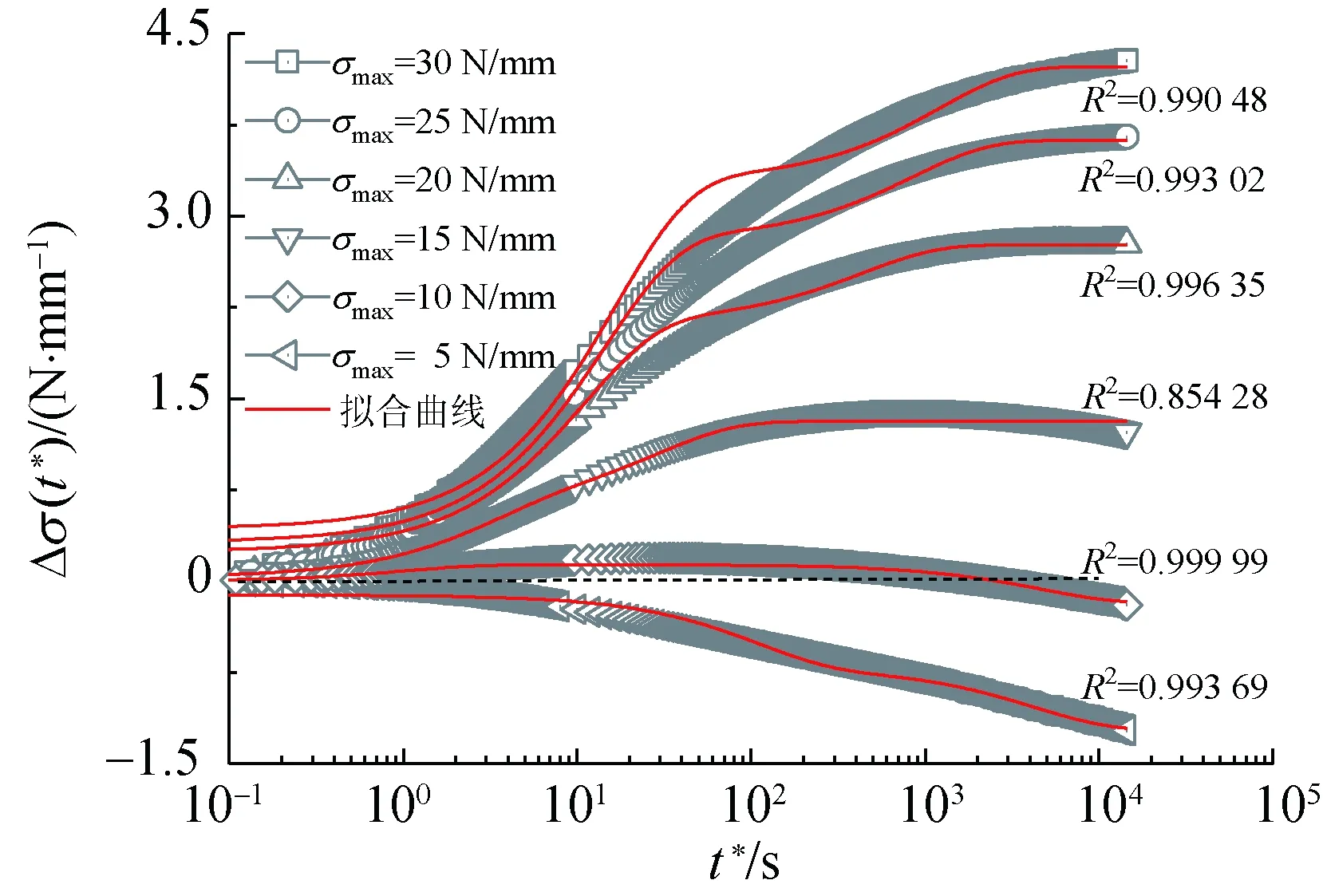
(a) 定常數廣義Maxwell模型

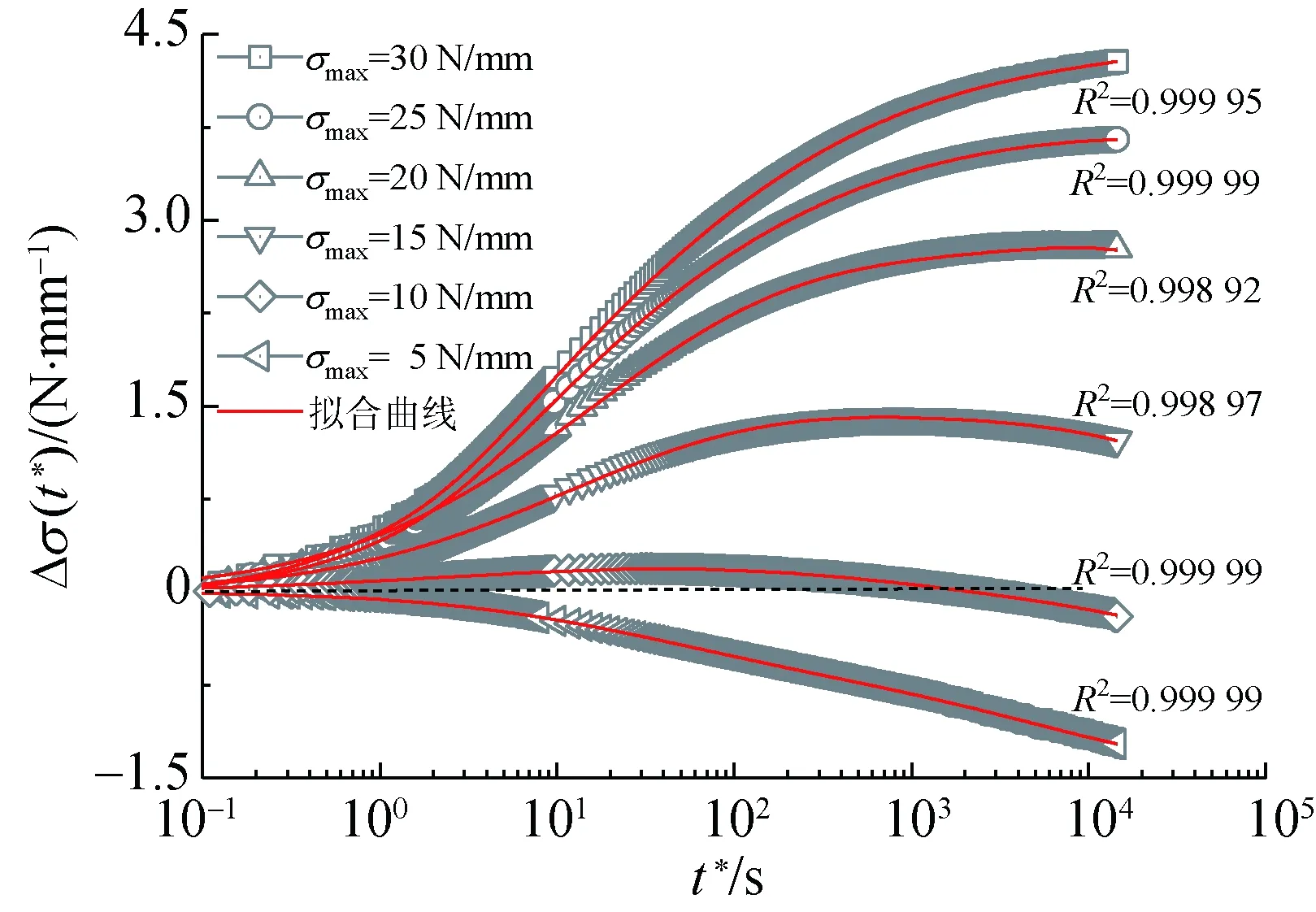
(b) 雙變參數廣義Maxwell模型

由圖6和圖7可知，相比定常數廣義Maxwell模型，雙變參數廣義Maxwell模型可較為準確地描述膜材松弛過程中應力變化量與松弛時間的變化情況，表明雙變參數廣義Maxwell模型適合擬合PVC膜材的簡單應力松弛、混合應力松弛及逆應力松弛行為。

3 結 語

本文以PVC膜材為研究對象，對其松弛前歷經應力回復后的應力松弛性能進行了測試與分析，并基于廣義Maxwell模型建立了雙變參數模型，試驗與分析結果如下：

(1) PVC膜材的應力松弛行為與松弛前應力回復階段的最大應力和初始松弛應力密切相關。當應力松弛前無應力回復時，材料表現(xiàn)典型的簡單應力松弛行為；應力回復量較小時，表現(xiàn)為混合應力松弛行為；應力回復量較大時，表現(xiàn)逆應力松弛行為。

(2) 模型擬合結果表明，相比定參數廣義Maxwell模型，雙變參數廣義Maxwell模型可較好地描述PVC膜材的簡單應力松弛、混合應力松弛以及逆應力松弛行為。

(3) 因應力松弛前歷經應力回復后的膜材對初始應力的保持能力較好，可調整現(xiàn)有膜結構表面預加張力的施加方法，減少膜結構表面張力損失，延長膜結構表面張力檢測和調整的時間間隔，減少膜結構建筑的后期維護工作量。

影響膜材復雜力學性能的因素，不僅與組成成分的力學性能相關，還與增強織物的編織結構、織物與涂覆層界面性能密切相關，本文僅從大分子鏈的角度闡述了應力回復對應力松弛性能的影響，膜材內部組分材料結構的變化，特別是經緯紗線屈曲結構的改變和轉化對應力回復條件下的應力松弛纖維的影響，還需做深入的研究。

因不同膜材組分材料的差異性和結構的多樣性，不同膜材表現(xiàn)出不同的黏彈性力學性質，在預加張力確定的前提下，針對應力回復前最大載荷的優(yōu)選，需要做進一步研究。

建筑膜結構用膜材的黏彈特性較為復雜，后續(xù)需對不同加載/卸載速度和溫度下的長時間應力松弛行為進行研究。