一類具有非局部項的捕食食餌模型的動力學分析
張國穎, 彭亞紅
(東華大學 理學院, 上海 201620)
捕食食餌模型在數學和生物學中扮演著非常重要的角色[1-2]。為了使該模型的適用范圍更廣泛,以及描述更加貼近現實,研究人員對捕食食餌模型進行了改進。例如在文獻[3-4]中,研究者們用食餌種群的平方根描述捕食者與食餌之間的相互作用,得到了更加精確的模擬捕食者與食餌之間關系的模型如式(1)所示。
(1)
式中:X(t)和Y(t)分別表示t時刻的食餌與捕食者的密度;r和K分別表示食餌種群的增長率和環境容納量;s表示沒有食餌時捕食者的死亡率;α表示捕食者對食餌的搜索效率;c表示生物量之間的轉化系數;th表示捕食者對食餌的平均處理時間。
Yuan等[5]把捕食食餌模型中捕食者的一次死亡率改為二次死亡率,對模型(1)進行如下無量綱變換:
并對其他參數作如下變換:
(2)
式中:d1和d2分別表示食餌和捕食者的擴散系數;uxx和vxx分別表示食餌和捕食者對x的二階偏導。
當假設捕食者對食餌的平均處理時間為0(即a=0)時,模型(2)可簡化為
(3)
Yuan等[5]利用線性化方法分析了模型(3)產生斑圖的條件,并利用標準多尺度分析方法建立了振幅方程,以及通過數值模擬展示了模型(3)的點狀斑圖、條狀斑圖和點條混合斑圖3種斑圖形態。而Xu等[6]考慮到捕食者和食餌之間的生物轉換量存在延遲現象,在模型(3)中引入時滯,選擇時滯項作為分支參數,研究了相應模型常微分系統正平衡點的穩定性和霍普分支的存在性。Liu等[7]選擇捕食者的一次死亡率,在齊次紐曼邊界條件下,將prey-taxis引入捕食食餌模型,研究了相應模型在初邊值條件下解的全局存在性,分析了正平衡點的存在性和穩定性,并利用抽象分支理論,以prey-taxis項作為分支參數,研究了非常數正解的穩定性以及穩態解的分支情況。

(4)
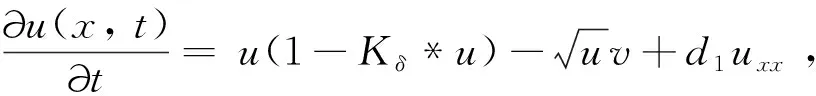
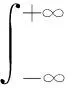

從生物角度而言,局部的反應擴散方程只能對位于一個空間點的個體與位于同一位置點的個體相互作用的情況進行建模,而非局部項描述兩個物種的個體都可以從一個空間點移動到另一個空間點。核函數Kδ(x-y)表示消耗強度,測量位于空間點x的獵物與位于空間點y的獵物之間的競爭效率。由于不同個體的消費地點可以重疊,獵物之間開始爭奪資源。核函數通常取標準概率密度函數。已有的研究中常用核函數包括以下3種:
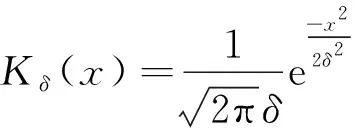

例如,文獻[9]分別選取以上3種核函數,研究了具有非局部項的兩類捕食食餌模型,討論了非局部項對正平衡點的影響;Sherratt[10]也選取以上3種核函數,研究了具有非局部擴散項的微分方程的周期行波解。
若核函數分別取高斯函數和分段函數,那么得到下文模型(5)的特征方程都是超越方程,因此只能采用數值方法去分析模型的動力學行為。本文為了更加清楚地從數學理論上借助參數展現出非局部項的影響,選擇拉普拉斯函數進行詳細的分析與討論。
(5)
本文主要研究無界區域(-∞, +∞)中非局部項對模型(5)正平衡點穩定性的影響,以及模型(5)產生圖靈分支的條件,進而通過數值模擬例證了理論結果。
1 模型(5)正平衡點的穩定性分析
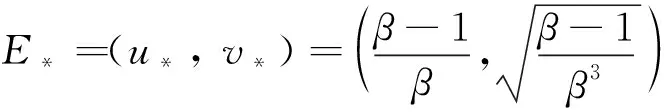
(6)
對模型(6)關于x作傅里葉變換為
(7)
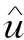
模型(7)的特征方程為
λ2-Tkλ+Dk=0,k>0
其中
(8)
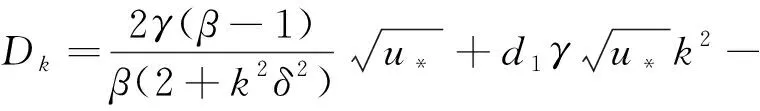
(9)
關于Tk和Dk給出如下兩個引理。
引理1設d1,d2,δ和γ都是正數,β>1。
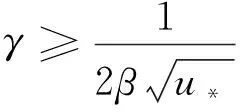
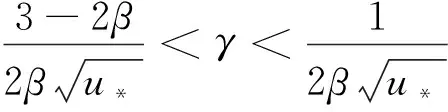
(10)
其中
(11)
(12)
(13)
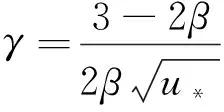
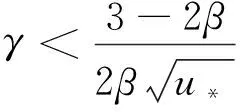
證明由式(8)可得
(14)
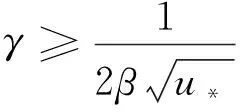
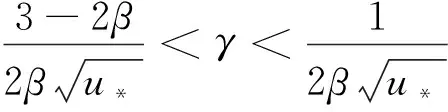
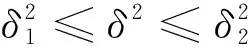
由于
且
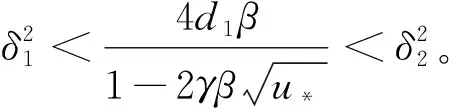
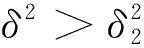
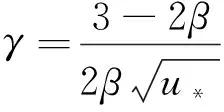
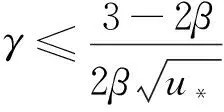
綜上可知,引理1成立,證畢。
引理2設d1,d2,δ和γ都是正數,β>1。

(15)
其中
(16)
(17)
(18)
g(k2)=-2d1βδ2k4+(δ2-4d1β)k2+2(3-2β)
(19)
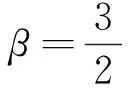

證明由式(9)可知
其中,g(k2)由式(19)給出。
其余的證明完全類似于引理1的證明,引理2結論成立。證畢。
結合引理1和引理2,得定理1。
定理1d1,d2,δ和γ都是正數,且β>1。
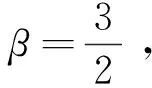
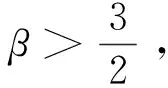
證明
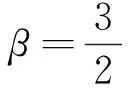

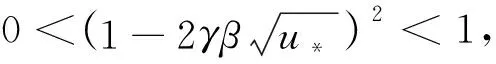
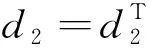
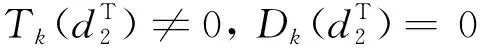
由引理1、引理2和條件H1,有定理2成立。
定理2d1,d2,γ和δ都是正數,β>1。

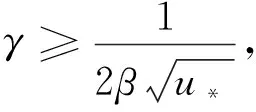
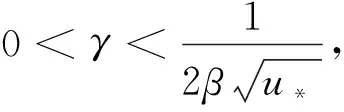
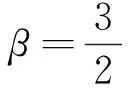
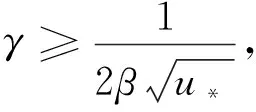

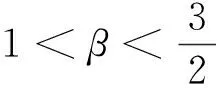
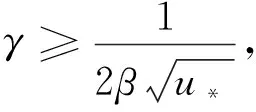
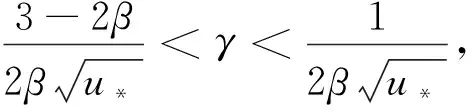
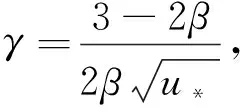
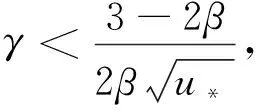
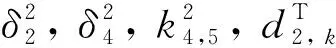
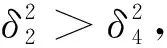
(20)
且
(21)

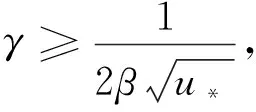
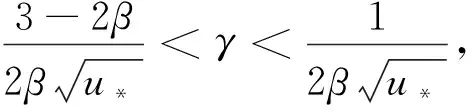
其中
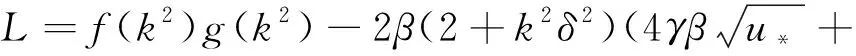
(22)
f(k2),g(k2)分別由式(13)和(19)給出,A(k2),B(k2),C(k2),D(k2)由式(21)給出。
由于
且
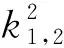

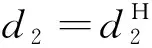
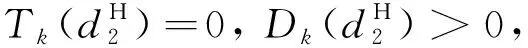
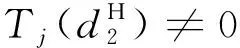
2 數值模擬
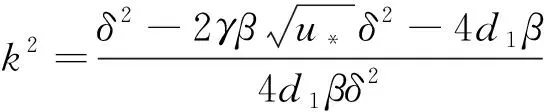
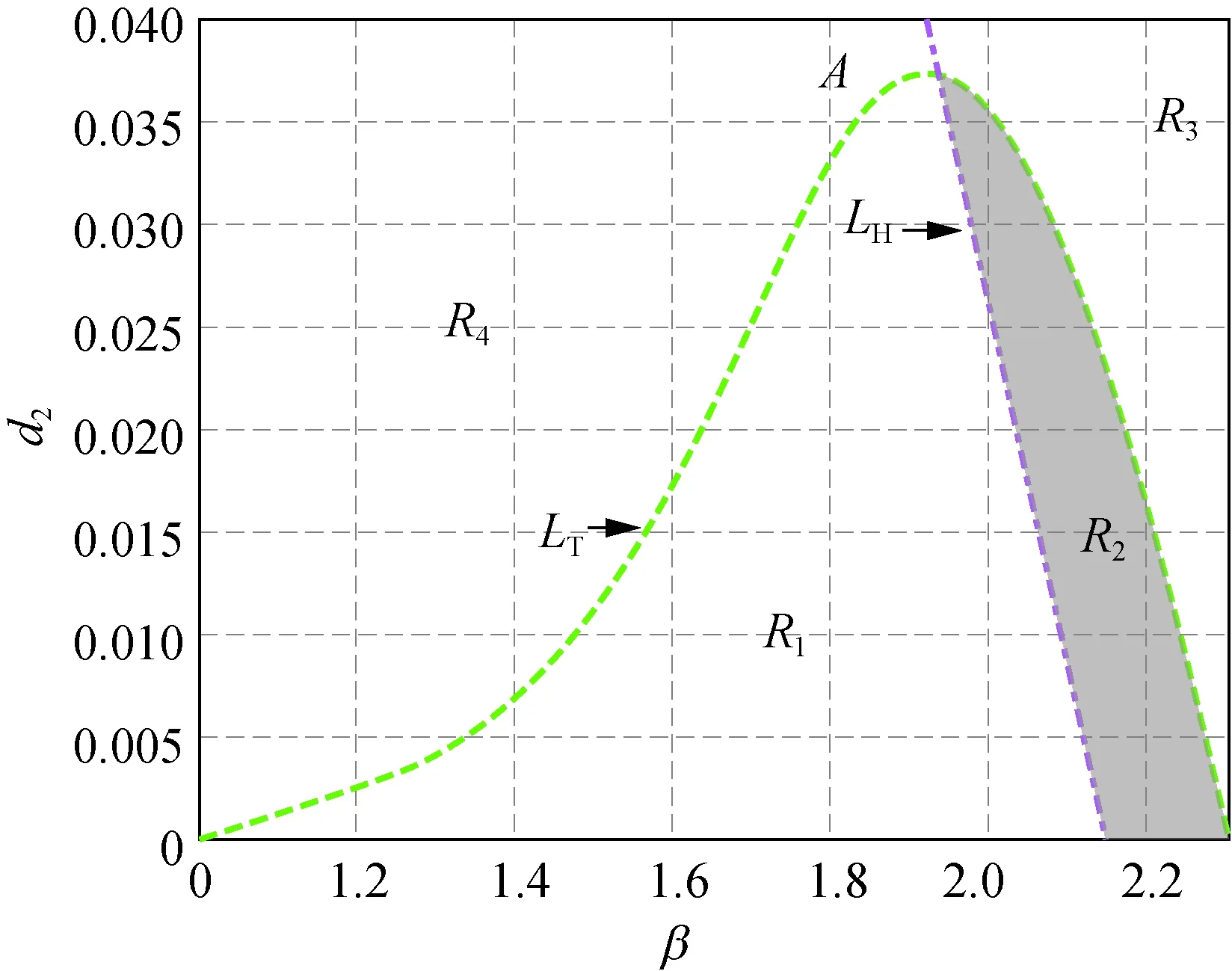
(a) δ=2.500

(b) δ=2.657
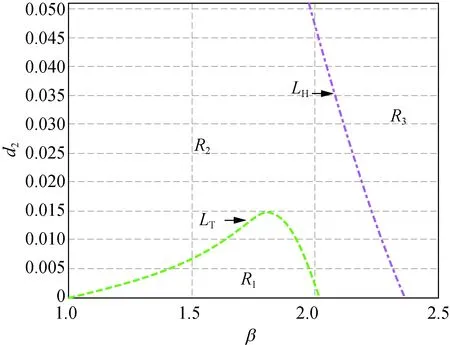
(c) δ=3.000
在圖1中,曲線LH右(左)方有不等式Tmax<0(Tmax>0)成立;曲線LT的上(下)方有不等式Dmin<0(Dmin>0)成立。在圖1(a)中,取δ=2.500時,曲線LH和LT相交于點A(1.933 , 0.037),此時LH和LT所圍成的陰影區域R2中,不等式Tmax<0和Dmin>0同時成立,即R2為模型(5)正平衡點的穩定性區域。隨著δ增大,當取δ=2.657時,在圖1(b)中,曲線LH和LT相切于點B(2.16 0, 0.007)。δ繼續增大,當取δ=3.000時就得到圖1(c),此時曲線LH和LT相分離。所以圖1中隨著δ從2.500增加到2.657直到3.000,陰影區域逐漸變小,直到消失,也即隨著δ的變化,模型(5)正平衡點的穩定性被破壞。
但是,當δ從3.000繼續增大到3.300時,曲線LH與LT會重新出現交點,也即正平衡點的穩定區域會隨著δ的增大重新出現。接下來分別取δ=3.300,4.000,5.000和6.000時得到圖2。
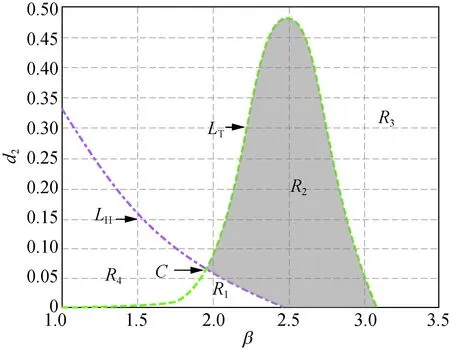
(a) δ=3.300
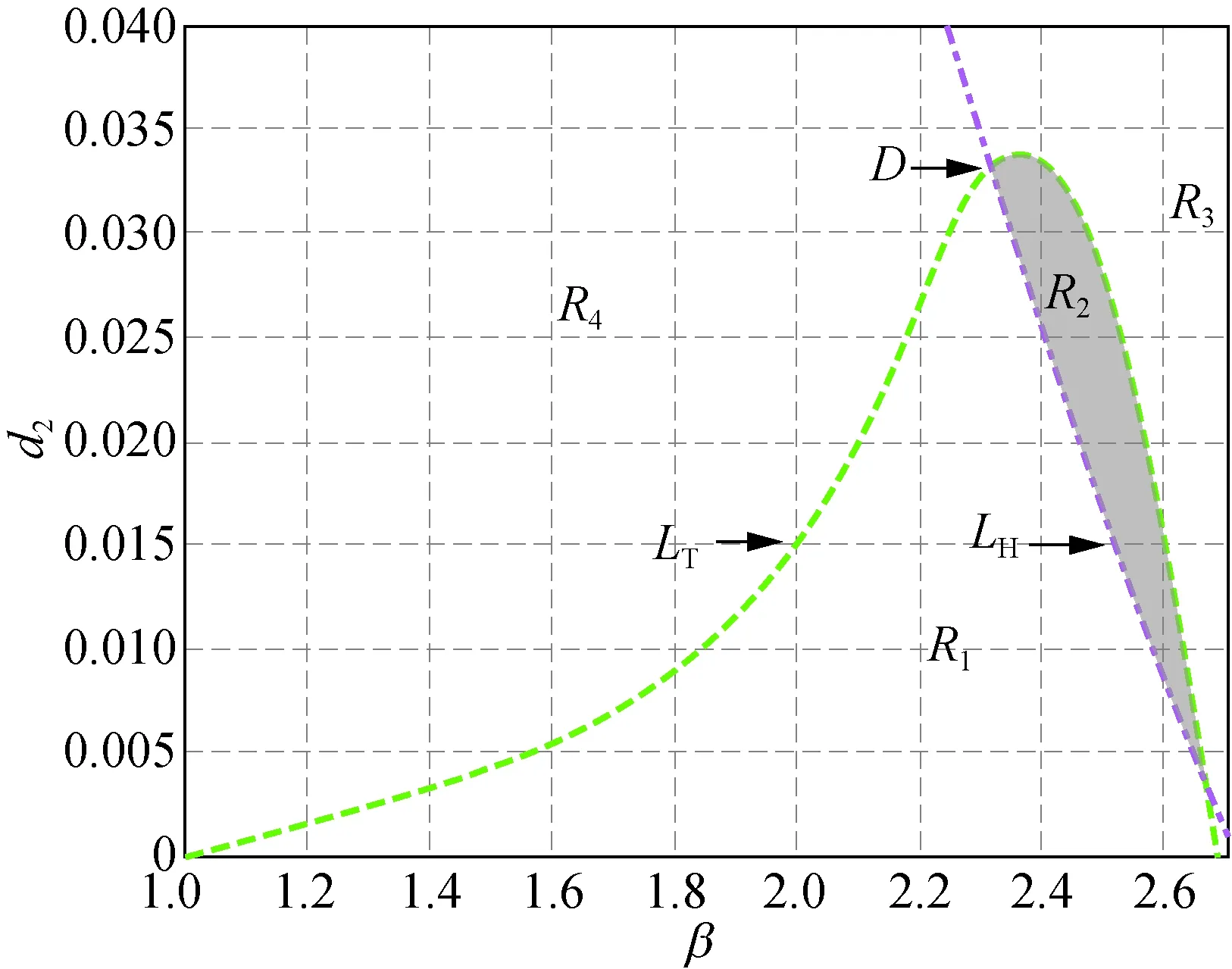
(b) δ=4.000
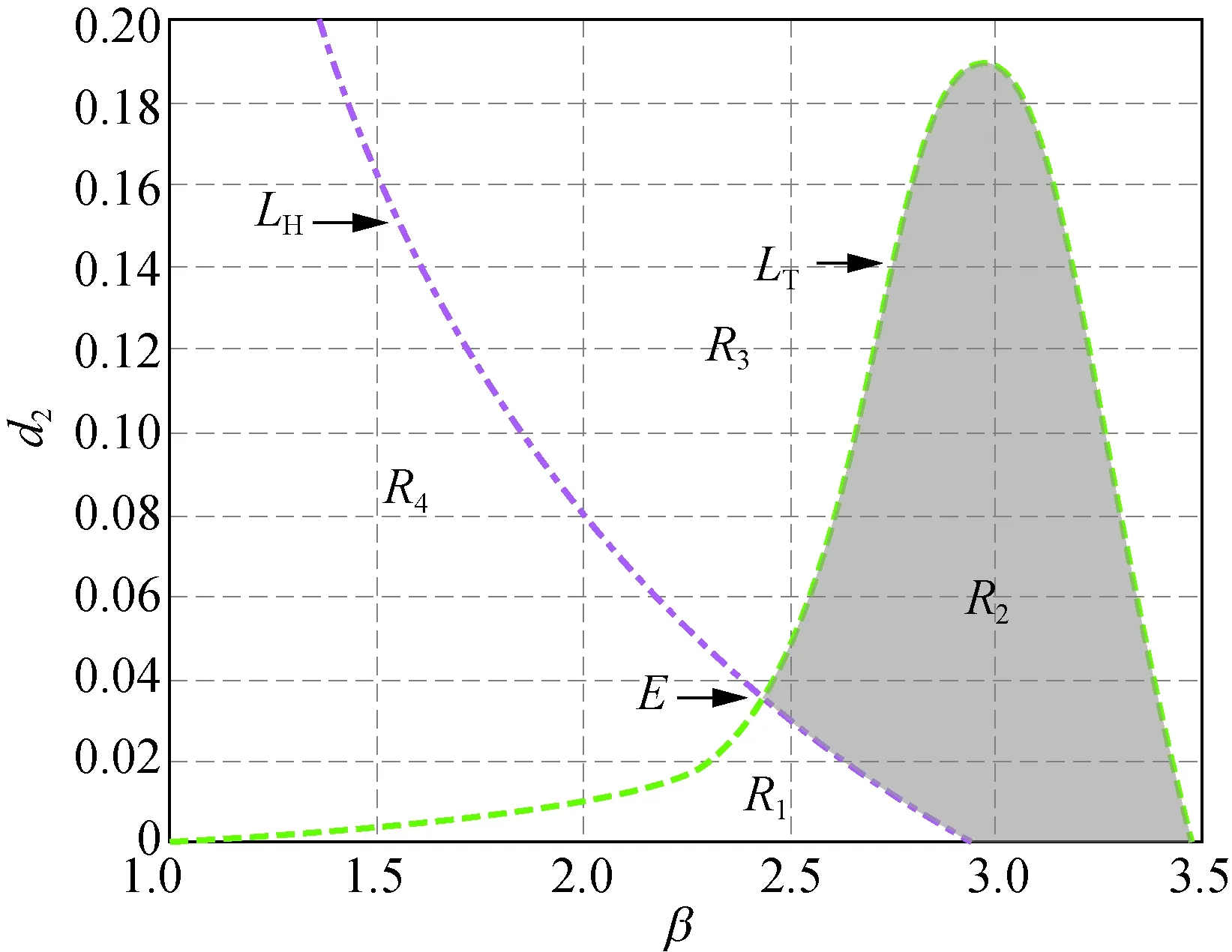
(c) δ=5.000
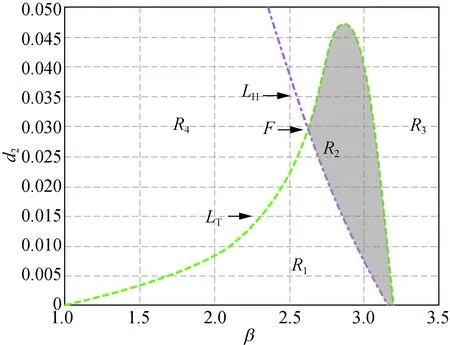
(d) δ=6.000
在圖2中,曲線LH和LT分別相交于點C(1.948, 0.064),D(2.314, 0.033),E(2.429, 0.036)和F(2.610, 0.031),陰影區域R2為穩定性區域。由此可知,隨著δ的增加,陰影區域的面積會發生變化,并且陰影區域將沿著β軸后移。圖2與圖1相比較可知,當δ>3.300時,模型(5)正平衡點穩定區域將一直存在。
此外,在圖1和圖2中,區域R1中Tmax>0且Dmin>0成立,此時存在k>0使得Tk>0,稱R1為霍普區域;區域R3中Tmax<0且Dmin<0成立,此時存在k>0使得Dk<0,稱R3為圖靈區域。圖1(a)和圖2(a)~(d)中的區域R4,以及圖1(b)~(c)中區域的R2都有Tmax>0及Dmin<0成立,故稱圖1(a)和圖2(a)~(d)中的區域R4,以及圖1(b)~(c)中區域的R2為圖靈霍普區域。
3 結 語
本文將非局部項引入具有二次死亡率的捕食食餌模型,選擇拉普拉斯核函數作為空間卷積項,研究了非局部項對模型(5)正平衡點穩定性的影響。研究表明,隨著非局部項中參數δ的變化,正平衡點的穩定性區域也發生變化。數值模擬例證了理論結果,并且展示出了非局部項的存在甚至可以使模型(5)正平衡點的穩定性區域完全消失的現象。

