如何拓展課堂教學(xué)的深層次思維

唐池

在日常的教學(xué)過程中我們的老師注重對學(xué)生知識的傳授，注重對學(xué)生應(yīng)試能力的培養(yǎng)，卻忽視了對學(xué)生思維的啟發(fā)。注重淺層的知識講解，忽視深層次能力的開發(fā)。這就導(dǎo)致我們的學(xué)生數(shù)學(xué)學(xué)習(xí)總是停留在知識和概念的記憶上，并沒有真正理解為什么是這樣的，更沒有進行深層次探索概念的來龍去脈。這樣淺層次的教學(xué)顯然不適合當前數(shù)學(xué)教學(xué)的要求。然而轉(zhuǎn)變?nèi)缃竦哪w淺教學(xué)方式，不但要向?qū)W生傳授書本上的知識概念，更要利用全面探索性的深度教學(xué)方法讓學(xué)生理解其內(nèi)在的邏輯關(guān)系，啟發(fā)學(xué)生思維，實現(xiàn)小學(xué)數(shù)學(xué)的深度教學(xué)，使他們對知識掌握得更加透徹，更加靈活。

現(xiàn)以范安東老師執(zhí)教的北師大版五年級下冊數(shù)學(xué)分數(shù)乘法（3）為例，在教學(xué)過程中，學(xué)生已有前兩個小節(jié)的學(xué)習(xí)，本課時的教學(xué)將在一定程度上讓學(xué)生根據(jù)已經(jīng)學(xué)過的知識，進行類比分析，對照學(xué)習(xí)。但分數(shù)乘分數(shù)與之前的最大不同在于分數(shù)乘整數(shù)可以根據(jù)乘法的意義解釋。然而對于分數(shù)乘分數(shù)而言，在學(xué)生已有的認知結(jié)構(gòu)中，并沒有相似的解決方法和案例。

在新知識的教學(xué)過程中，就必定會存在如下的問題亟待解決：1.如何讓學(xué)生去理解兩個分數(shù)之間存在的聯(lián)系;2.如何進行單位 “1”的轉(zhuǎn)換;3.如何根據(jù)學(xué)過的知識來解決未知的問題;4.以及如何統(tǒng)一整數(shù)乘分數(shù)，分數(shù)乘分數(shù)之間的相互關(guān)系。針對這一連串問題，首先要明確的把握學(xué)生認知結(jié)構(gòu)中已有的相關(guān)經(jīng)驗。如：轉(zhuǎn)化的思想、數(shù)形結(jié)合的思想、歸納概括的思想等等。這些思想是學(xué)生能把控和熟練應(yīng)用的基本技能。然而如何才能把這些問題深入下去呢？

筆者認為要實現(xiàn)深度教學(xué)需要從問題提出的深度、探索方法的深度、思維變通的深度、知識聯(lián)系的深度這四個方面考慮，這四個方面也是對應(yīng)的深度教學(xué)的四個基本特征。

一、問題提出的深度

課例片段1：

師：你對莊子的這句話是怎樣理解的“一尺之棰，日取一半”。

師：觀察上面的圖和算式你有什么發(fā)現(xiàn)和想說的？

針對于這個問題的提出安東老師讓學(xué)生通過直觀圖，去猜想分數(shù)乘分數(shù)的方法，這里老師重視啟發(fā)學(xué)生的思維，幫助學(xué)生將知識轉(zhuǎn)化為智慧。學(xué)生將會有意識地進行知識的探索，培養(yǎng)他們思維的靈活性和敏捷性。

老師通過提出質(zhì)疑，給予學(xué)生從不同角度思考問題的方法，當學(xué)生面對兩個假設(shè)時，會充分調(diào)動大腦中的知識去解決這個問題，在發(fā)揮學(xué)生提出問題能力的同時，又開闊學(xué)生的思維，激發(fā)學(xué)生探索新知的欲望。從另一層面上來講加大了問題的深度和思考的難度，讓學(xué)生在差異中尋找真諦。克服了傳統(tǒng)教學(xué)中，單一片面的問題思考模式。

在問題的設(shè)計上，為了深入討論分數(shù)乘分數(shù)的方法，在經(jīng)歷猜想---假設(shè)的環(huán)節(jié)之后，舉例驗證結(jié)論，兩個分數(shù)的選擇也是指教老師在思考之后有意設(shè)置的，目的在于讓問題具有探究性，拓展性和遷移性從而幫助實現(xiàn)教學(xué)的深度。

二、方法探索的深度

課例片段2：

生：利用畫圖的方法來解決（學(xué)生活動）

（出現(xiàn)問題：在安東老師巡視過程中，多數(shù)學(xué)生都受到前面方法的影響，采用畫線段圖的方式來解決這個問題，但在實際的操作過程中，發(fā)現(xiàn)：和這兩個分數(shù)在表示的過程中，出現(xiàn)了困難）

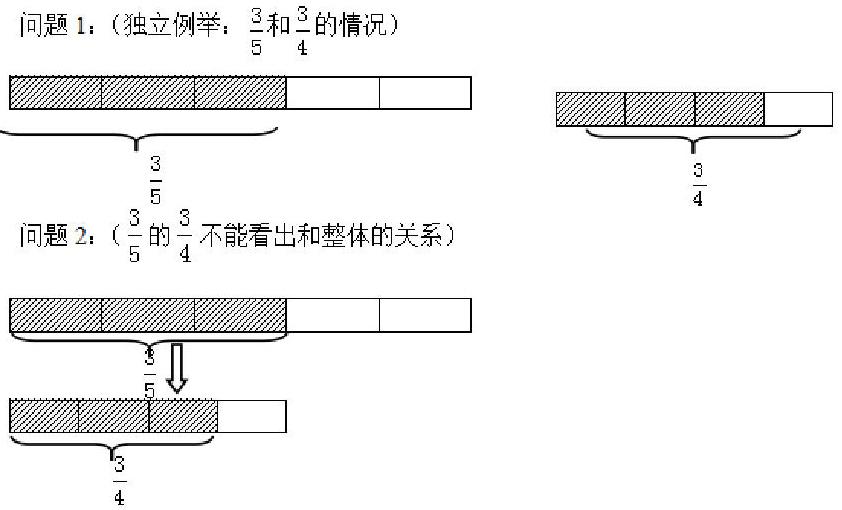
問題1：（獨立例舉：和的情況）

問題2：（的不能看出和整體的關(guān)系）

上面兩種學(xué)生思考的過程，都出現(xiàn)同一問題，沒能很直觀的看出的具體是多少，究其原因在于學(xué)生在思考的時候采用一維線段圖。不能將2個單位“1”很好的集合起來，而是分別表示出了兩個分數(shù)，但單位“1”卻是隔離開的，并未去深入溝通兩者的關(guān)系。

師：剛才同學(xué)們都表示出了自己的方法，卻發(fā)現(xiàn)并沒有真正表示出的結(jié)果，那我們換一種思路，能不能用面來表示和呢？

在方法探究的過程中，針對學(xué)生出現(xiàn)的問題，教師作為課堂的組織者、引導(dǎo)者和問題出現(xiàn)后的解疑者，，應(yīng)該從學(xué)生與生俱來的好奇心和探索欲出發(fā)，給予學(xué)生一定的幫助。“指導(dǎo)和提示，讓他們靈活的運用已有的知識對問題進行自主探究、交流、創(chuàng)新， 避免學(xué)生的思維定式，培養(yǎng)學(xué)生多角度，多方法思考問題，學(xué)會在已有的知識和方法無法解決問題的時候，轉(zhuǎn)換思路，這對于開發(fā)學(xué)生思維是非常有益的。”盡管在實施的過程中會出現(xiàn)問題，但教師要正確的引導(dǎo)學(xué)生從一維圖形的困境中找到解決問題的方法，從而過度到利用二維圖形來解決問題。

三、思維變通的深度

分析上面的教學(xué)片段，我們不難發(fā)現(xiàn)：教學(xué)過程中，對于學(xué)生思維能力的挖掘，是體現(xiàn)深度教學(xué)的關(guān)鍵之一，學(xué)生在思考問題過程中，會不會把已有知識和生活經(jīng)驗結(jié)合，甚至是教師給出的事例聯(lián)系起來，綜合所有的資源來解決問題。“在這里思維的深度體現(xiàn)了數(shù)學(xué)學(xué)科的教學(xué)本質(zhì)，另一方面數(shù)學(xué)深度教學(xué)能夠很好地培養(yǎng)學(xué)生分析、歸納、綜合、類比、演繹、推理等數(shù)學(xué)思維方式，從而在幫助學(xué)生掌握一定的探究性學(xué)習(xí)方法的同時，也培養(yǎng)了學(xué)生的邏輯思維、抽象思維等能力。”

四、知識聯(lián)系的深度

這里也讓我們體會到：學(xué)生學(xué)習(xí)知識不能機械的死記數(shù)學(xué)概念和數(shù)學(xué)公式，而是要有意識的建構(gòu)數(shù)學(xué)知識體系。通過前后知識的聯(lián)系，從解決問題的角度出發(fā)，我們的教師要設(shè)計一些深層次的具有挑戰(zhàn)性任務(wù)的問題與活動，讓學(xué)生深刻的理解數(shù)學(xué)知識之間的邏輯關(guān)系和內(nèi)在聯(lián)系，最終要讓我們的學(xué)生能應(yīng)用學(xué)到的知識去解決實際生活中的數(shù)學(xué)問題。

在平時的教學(xué)過程中，如何讓小學(xué)數(shù)學(xué)教學(xué)走向深度，這是一個值得深入探討的問題，但是作為教師我們在實現(xiàn)深度教學(xué)的過程中，一定不能忽略從學(xué)生與生俱來的好奇心和探索欲出發(fā)，幫助他們靈活運用已學(xué)到的知識進行自主探究、交流、創(chuàng)新，這對于開發(fā)學(xué)生思維是非常有益的。也是實現(xiàn)深度教學(xué)最根本的保證。