基于K-medoids 方法的大學生體質健康分類研究
胡世平,李博,賈年
(西華大學計算機與軟件工程學院,成都610039)
0 引言
當今,健康問題越來越受人們的關注。在2017年,習近平主席在十九大報告中提出了健康中國的發展戰略,這同時也表明國家對全民健康的重視。21 世紀,社會的競爭壓力也越來越激烈,它不僅包括表面的智力競爭,同時也是對身體、心理等方面的考驗,這些非智力因素同時決定著競爭的成敗,而決定這方面的重要因素就是身體健康狀況,但是目前大學生中一些群體缺乏鍛煉意識,對科學鍛煉身體的意識薄弱[1]。因此有效科學的提高大學生身體健康素質才是關鍵,而運動處方則是有效和科學提高身體健康的最佳方法[2]。關于運動處方的研究在國內越來越多,部分領域也愈加成熟,例如健身運動處方,可以針對不同年齡段,采取合適的運動處方來提高身體素質和預防疾病。醫生往往也會根據經驗給一些病人開出適合的運動處方。但是目前高校的學生數量越來越多,面對大量的學生數據,老師很難為每個學生設計個性化運動處方、從而高效科學地提高學生的身體素質。
因此采用合理的方法去分析評價體測數據和對學生進行合理的分類,并且如何合理地推薦處方是目前研究的重點。只有科學和有效的運動處方方案,才能夠更好地讓學生進行自我健康的體質管理[3-4]。為此,本文提出了一種基于無監督學習的大學生健康數據分類方法。該方法使用大學生的測試數據的BMI、肺活量、體前屈、立定跳遠、50 米跑、1000 米跑(男)或800米(女)、引體向上(男)或仰臥起坐(女)作為輸入數據,通過K-medoids 聚類算法,將體質類似的學生分在一起,老師可以根據不同的體質的學生,制定更針對性的個性化運動處方,科學高效地提高大學生身體素質。
1 K-medoids算法介紹
K-medoids 算法被稱為K 中心點算法,也是一種常用的聚類算法,與K-means 聚類算法相似,也具有能夠處理大型數據集,且最后聚類結果中簇與簇之間分離明顯的優點。與K-means 相比,K-medoids 算法對噪聲的魯棒性更好,對于簇中那些脫離中心點很遠的點不是很敏感,這樣噪點對于簇的劃分的影響就會大大減少。就因如此K-medoids 也被認為是對K-means的改進,但由于對于中心點更新時的計算量要更大,所以時間復雜度比k-means 要高[5]。
為對比聚類效果,本文采用不同數量集下K-me?doids 算法與K-means 算的戴維森堡丁指數(DBI),如表1 所示,用DBI 去進行聚類優劣比較發現,當學生體測數據變多時,K-medoids 算法的DBI 是小于Kmeans 算法的DBI,DBI 值小意味著類內距離越小,同時類間距離越大,聚類效果越好。可以看出K-medoids算法在多數據的情況下的聚類效果要好于K-means 算法,證明其在做大量學生體測數據進行聚類分類時的效果更好,且其魯棒性也比K-means 算法好。
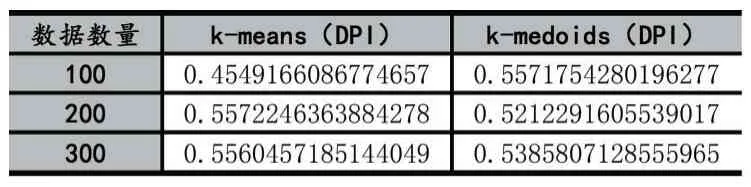
表1 戴維森堡丁指數(DBI)值比較
2 基于K-medoids方法的學生體質健康分類方法
2.1 數據收集
本文采用的是某高校的體質健康數據進行分析,該數據包括學生的個人信息以及體測數據,其中BMI、肺活量、體前屈、立定跳遠、50 米跑、1000 米跑(男)或800 米(女)、引體向上(男)或仰臥起坐(女)等數據作為此次試驗的輸入數據,對應的也是《國家學生體質健康標準》中的8 項。
2.2 數據預處理
由于大學生體測數據量比較大,有可能含有許多噪聲數據,我們先將數據進行整理,去除某些測試屬性缺失的學生,如短跑,肺活量為0 的學生,部分體測數據如表2 所示。然后為了縮小不同的成績和不同的評價指標帶來的影響,我們將體測數據歸一化,數據被限定到[-1,1],這樣也有益于使用PCA 進行降維的時候表現的更好。歸一化的部分數據如表3 所示。

表2 部分體測數據數據
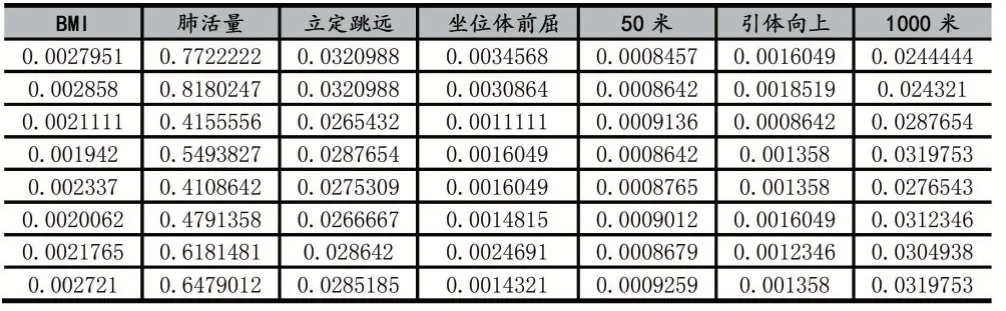
表3 歸一化后部分數據
2.3 數據處理
本方法對學生體測數據進行聚類分析,具體執行過程如下:
(1)首先,我們將采集到的6000 個學生體測數據放入矩陣,然后對數據進行預處理
(2)根據預處理過的學生數據矩陣來計算各個樣本點之間的歐式距離,放到矩陣D 中,并且確定聚類個數k(表示有k 種體質分類)
(3)隨機選取k 個中心點(每個中心點代表一個簇)
(4)根據距離矩陣D,將樣本點分到距離它最近的中心點的簇中
(5)計算各個簇中的樣本點到簇中其他樣本點的距離,求出距離最小樣本點作為新的中心點
(6)如果新的中心點集合與之前的中心點集合一樣或者迭代次數達到最高次數,算法終止,輸出最后一次各個簇中的樣本點,如果不一樣則返回(4)。
數據處理流程圖如圖1 所示。
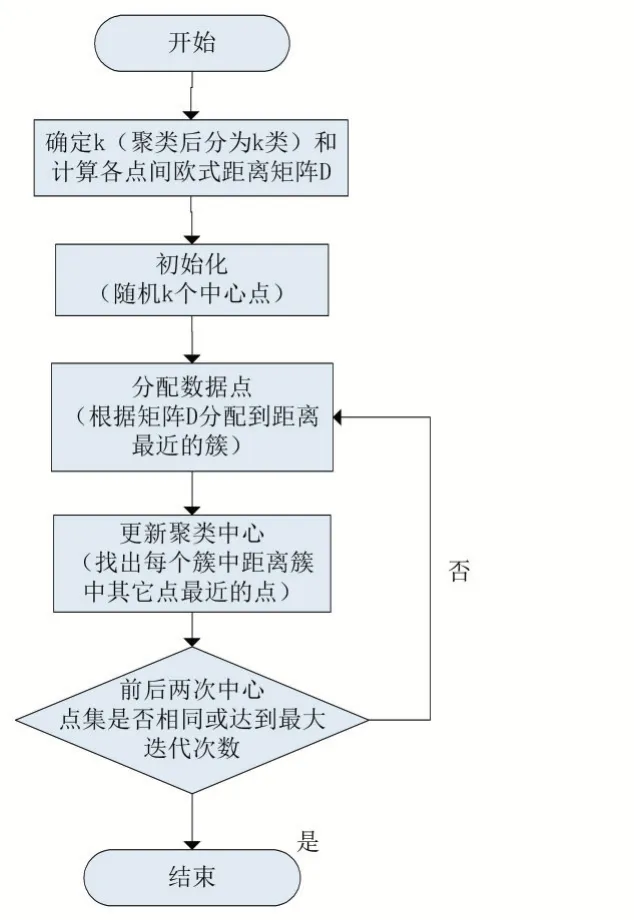
圖1 基于K-medoids方法的學生體質健康分類算法流程圖
2.4 實驗結果分析
隨機從數據庫抽取6000 條男生測試數據作為實驗數據。使用K-medoids 算法進行分析,將BMI、肺活量、體前屈、立定跳遠、50 米跑、1000 米跑(男)、引體向上(男)數據傳入,將分類的個數k 定為10,表示將分為十類。迭代次數選取100 次,如果中心點集合沒有變化或者達到最高次數還沒有收斂則選取最后一次的中心點集合作為中心點,每個簇的最后的中心點向量和每個簇的數量如表4 和表5 所示。
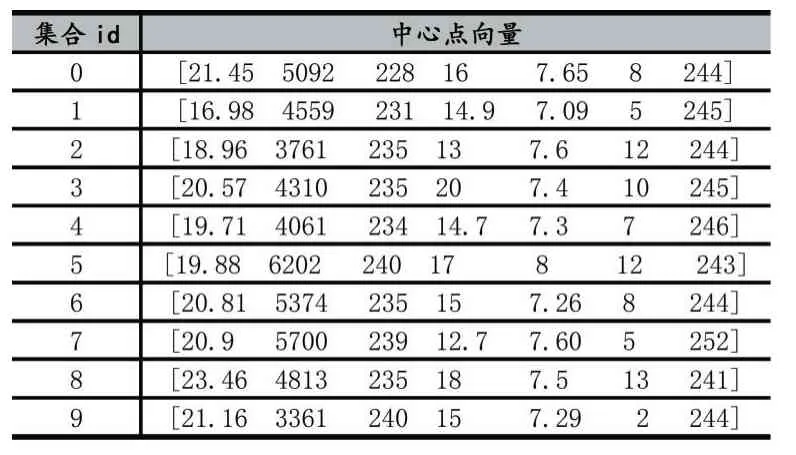
表4 中心點向量
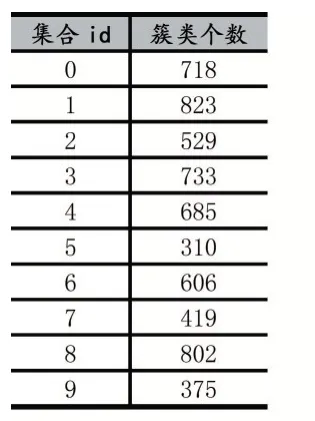
表5 每個集合中簇類的個數
將聚類結果用PCA(Principal Component Analysis,主成分分析)降維顯示如圖3 所示,PCA 能夠使新的低維數據集會盡可能地保留原始數據的變量結果,但是需要注意,通過PCA 降維實際上也損失了一些信息,通過查看pca.explained_variance_ratio_值得出[0.99781126,0.00157304],可以看到保留的兩個主成分,第一個主成分可以解釋原始變異的99.78%,第二個主成分可以解釋原始變異的0.15%。也就是說降成兩維后仍保留了原始信息的99.93%左右。通過K-medoids 聚類算法,觀察每個聚類特征,可以發現集合id5 中學生數據大部分為優秀且多個測試數據接近,集合id9 中,體測數據及格的居多且多個測試數據接近。這也表明該算法可以很好地讓體質相似的學生分在一起,方便老師對學生制定個性化的運動處方。
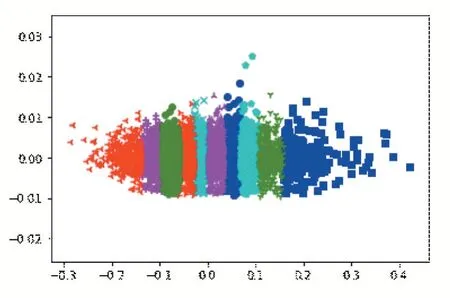
圖2 各個簇的分布情況
3 結語
由于大學生數量較大且體質測試數據沒有任何規律性,導致了很難從中找出規律,老師也很難為每個學生設計個性化運動處方,從而高效科學地提高學生的身體素質。通過本文的聚類分析,我們可以輕松地找出相似體質的學生,通過分類出的學生體質特點,采取針對性強、個性化的運動處方來鍛煉學生,可以更加有效科學地提高大學生的身體素質。

