基于線性二次滾動時域法的運載火箭發動機推力故障診斷

葉 松，陳 曦，熊寸平

(北京航天自動控制研究所，北京 100854)

0 引言

隨著航空航天技術的快速發展，運載火箭的組成越來越復雜，其可靠性和安全性問題日益突出[1]。故障診斷技術的應用，能夠及時檢測系統故障，提高系統的可靠性，同時為后續容錯控制奠定基礎。動力系統作為運載火箭的一個關鍵系統，為運載火箭提供動力，推動運載火箭前進。推力下降故障是動力系統故障類型之一，會導致系統性能退化甚至不穩定，因此研究推力下降故障診斷具有重要意義。

故障診斷包含故障檢測、估計與故障定位。故障檢測反映故障的發生，故障估計表征故障程度，故障定位表征故障發生的位置。故障診斷常用基于動態模型的方法[2-3]、基于信號處理[4-5]的方法以及基于知識[6-7]的方法。基于成熟的運載火箭建模理論，采用基于動態模型的方法更具有工程應用價值。

基于動態模型的非線性系統故障診斷方法主要有狀態估計法、參數估計法。前者通常對非線性模型的某些特征點進行線性化，利用建模誤差作為未知輸入并設計未知輸入觀測器獲取殘差，進行故障診斷，后者通常對非線性模型利用非線性參數估計的方法進行故障診斷。王青等[8]采用狀態估計法，基于線性化后的飛行器模型，設計降階故障檢測濾波器，在減少計算量的同時保證了故障檢測的快速性。符文星等[9]研究了基于強跟蹤濾波器的參數估計方法，對運載火箭的推力參數進行了正確估計。

本文結合狀態估計法與參數估計法，提出了一種基于擴展卡爾曼濾波器生成殘差，采用線性二次滾動時域算法[10]估計故障，并根據過載方向定位故障的方法，對發動機推力下降故障進行在線檢測與定位。最后將該方法進行數學仿真，驗證了算法的有效性。

1 數學模型

本文以運載火箭為例，火箭動力系統包含4臺搖擺發動機，其布局如圖1所示。

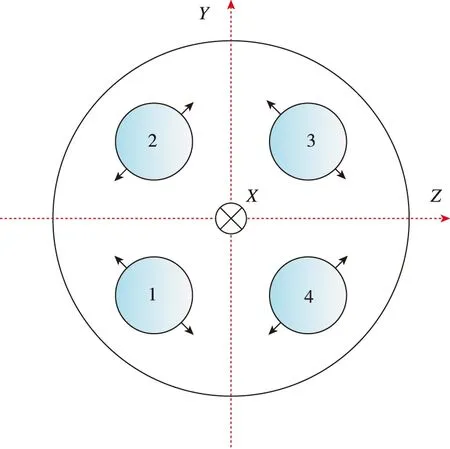
圖1 火箭發動機布局圖Fig.1 Distribution of launch vehicle power system

受地球自轉的影響，發射坐標系為動坐標系，這樣存在附加哥氏力和力矩、附加相對力和力矩的影響，但本方法中這些影響均可以視作濾波器噪聲，因此將發射坐標系視作慣性系，從而忽略附加哥氏力和力矩、附加相對力和力矩的影響，以突出研究的重點。簡化后的運載火箭動力學及運動學方程[11]

(1)

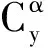
(2)

(3)

式中，γ為滾轉角，?為俯仰角，ψ為偏航角。

取狀態變量如下

(4)

記

可得

(5)

為簡化計算，取量測變量為除發動機推力外的12個狀態變量

yi=xi+vi

(6)

式中，i=1,2,…,12。v為白噪聲序列。

上述模型進行線性化和離散化并寫為如下非線性形式

x(k+1)=F(k,u(k),x(k))+Γ(k)v(k)

y(k+1)=H(k+1,x(k+1))+e(k+1)

(7)

式中，整數k≥0為離散時間變量，x為狀態變量，u為輸入向量，y為輸出變量。非線性函數F，H為狀態的一階連續偏導數，Γ為已知矩陣。系統噪聲v(k)、測量噪聲e(k)為高斯白噪聲，互不相關。在此基礎上，設計擴展狀態觀測器(Extended Kalman Filter，EKF)如下

X(k+1)=X(k+1,k)+K(k+1)[Z(k+

1)-H(k+1)X(k+1,k)]

(8)

濾波增益陣K為

K(k+1)=P(k+1,k)HT(k+1)·

1)+R(k+1)]-1

(9)

預報誤差協方差陣為

P(k+1,k)=Φ(k+1,k)P(k)ΦT(k+

1,k)+Q(k)

(10)

狀態估計誤差協方差陣為

P(k+1)=[I-K(k+1)H(k+1)]P(k+1,k)·
[I-K(k+1)H(k+1)]T+
K(k+1)R(k+1)K(k+1)T

(11)

式中,X(k+1,k)為狀態的一步預測值如下

X(k+1,k)=f(X(t))|X(t)=X(tk)

(12)

Φ(k+1,k)為狀態轉移矩陣如下

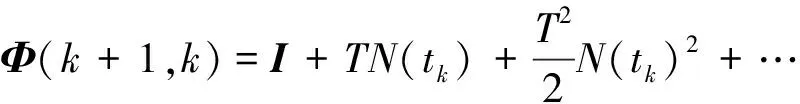
(13)

H(k+1)為量測轉移矩陣，根據狀態變量和量測變量的關系，可以得到H(k+1)為單位陣。

“我上一次到訪查謨-克什米爾大君的斯里那加宮殿時， 他們端出了三十個盤子，如果我說任何一個盤子上的寶石都能在市場賣得到一百萬元，恐怕是遠遠低估了這些寶物的美及它所代表的財富。”

將模型實時觀測到的某狀態量與EKF方法下狀態量的計算值作比較，可得到系統殘差預測向量

(14)

式中,r為1×n維。

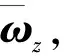
(15)

式中,rωz為1×n維。

2 故障診斷算法設計

考慮運載火箭推力下降故障，記推力下降程度為f，f∈(0,1)，0表示推力下降程度為0%，1表示推力下降程度為100%。當發動機發生推力故障時，推力Pf如下

Pf=(1-f)P

(16)

2.1 殘差表示

殘差數據Y為某個時間間隔內殘差向量rωz的采樣值，以如下形式表示

(17)

式中，tb為數據采樣開始的時間，Δ為采樣間隔，N為樣本的數量，f為故障程度。向量Y的大小為(N+1)×1。

2.2 靈敏度矩陣求解

假定動力系統運行正常，則零故障記為Y(tb,N,Δ;0)；若發生故障，獲得的殘差數據將進一步表示為Y(tb,N,Δ;f)。將故障殘差數據線性化處理，分為無故障殘差部分和故障相關部分，如下

Y(tb,N,Δ;f)≈Y(tb,N,Δ;0)+S(tb,N,Δ)f

(18)

式中，S為關于Y(tb,N,Δ;f)的最后一個參數f的(N+1)×1雅可比矩陣，稱為靈敏度矩陣。

(19)

無故障情況下的殘差為

r0(t)=r(t;f=0)

(20)

由于實際中殘差無法直接對故障求導，可通過下式求解靈敏度矩陣參數

(21)

式中，d是有限差分步長，與采樣時間保持一致。e為單位故障向量，表征1%的推力下降程度。通過下式對特征數據進行采樣來計算矩陣S。

(22)

2.3 估算算法

前文介紹了殘差向量Y以及靈敏度矩陣S的求解，下文對故障估算算法進行介紹。

對于實際系統，由于傳感器噪聲和建模誤差的存在，殘差不為零。將所有這些因素匯總在一個廣義的“噪聲”ew數據向量中。假設殘差數據向量Y的統計模型如下

Y=Sf+ew

(23)

通過對該殘差數據模型中的變量進行統計假設，可以得出故障參數的估計值。一種設計方法是將統計參數視為估算算法的調整參數，可以對這些參數進行調整，以實現算法的合理實用性能。基于此，假設噪聲ew是具有協方差矩陣V的正態分布向量。同時假定要估計的未知故障向量f是獨立于(噪聲ew)的隨機變量，并且為具有協方差矩陣R的正態分布向量。在這種情況下，可以從噪聲數據中獲得故障向量f的最佳統計估計值

(24)

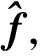
在此過程中如果忽略傳感器噪聲，唯一建模誤差是殘差與故障矢量關系式中一階近似的線性化誤差。在實施估計算法時，協方差矩陣V設為單位矩陣，這對應于所有觀察通道中存在的相同幅度的白噪聲。

將故障的協方差矩陣R選擇為

R=F2

(25)

F具有預期故障強度的含義。可以基于故障性質的知識來設置故障強度，實際中通過多次測試獲取。

故障向量可以從整個飛行過程中收集的數據集作為一個批處理估計獲得，但是，可能需要在整個飛行過程中計算和更新估算值，以便在線估算和觀察不斷發展的故障。為滿足此需求，以滾動時域的形式實現用于故障參數估計的GLS算法。在每個時間步，滾動時域算法使用N個最新數據點來計算故障參數矢量的估計值。此估算形式如下

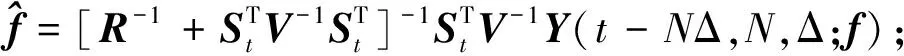
(26)

由于一種故障類型對應一種故障強度，因此針對單一的推力下降故障，故障協方差陣維數恒為1×1。因此選用單一殘差向量ωz保證公式(25)的維數匹配，滿足對故障敏感的殘差均可選用。

2.4 故障定位

基于殘差信息的故障檢測僅能反映整體的故障時刻以及故障程度，當4臺發動機的某一臺發生故障時，僅基于殘差無法區分4臺發動機的故障信息。因此提出一種基于故障時刻的過載方向信息定位故障的方法。進行仿真分析，當動力系統4臺發動機分別在25 s發生30%推力下降故障時，ny(箭體系y1方向過載),nz(箭體系z1方向過載)狀態如圖2、圖3所示。

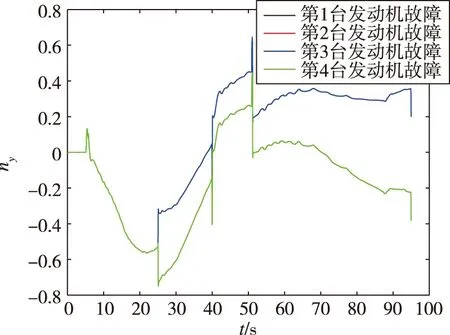
圖2 4臺發動機分別故障下過載ny響應曲線Fig.2 ny response with each individual engine fault

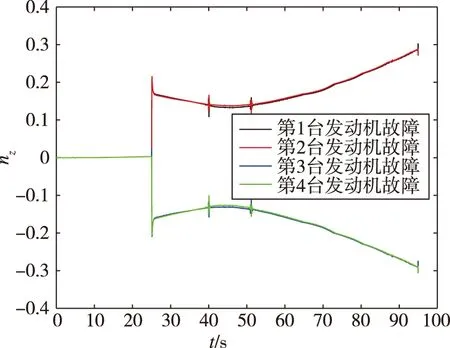
圖3 4臺發動機分別故障下過載nz響應曲線Fig.3 nz response with each individual engine fault

由圖2、圖3可以得知，過載ny在第2，3臺發動機故障響應相似，第1，4臺發動機故障響應相似。過載nz的第1，2臺發動機故障響應相似，第3，4臺發動機故障響應相似。因此檢測出故障發生后，可根據ny，nz的突變方向，綜合判定故障發動機的編號。利用這種特性，可以應用于故障檢測方法中。

2.5 算法流程

提出的方法分為生成殘差、估計算法與故障定位3部分。

第1部分在推力無故障情況下，以P，vx，vy，vz，ωx，ωy，ωz，x，y，z，φ，ψ，γ作為輸入數據，基于預測模型，利用EKF方法得到除推力P外的預測數據計算值，計算殘差。

由上述狀態量計算的殘差不能完全反映推力下降故障，通過分析殘差數據vx，vy，vz，ωx，ωy，ωz,x,y,z,φ,Ψ,γ的曲線發現，推力下降故障僅對vx，vy，vz，ωx，ωy，ωz影響非常比較明顯。其中，vy，ωy與ωz在某些時刻的殘差有明顯突變，且故障后一段時間能夠將系統控制到穩定狀態，符合實際情況，因此采用ωz計算殘差。

將無故障的狀態參數ωz與預測值做差，即得到殘差r0。同理，在1%故障下ωz實際值與預測值做差對應生成殘差rf_1%。

在推力故障情況下，通過推力P，由EKF計算故障下的狀態參數ωz，最終生成rf。

3 仿真分析

3.1 單臺分析

(1)不同采樣長度N對仿真結果的影響

設定50 s時發生50%的推力下降，考慮到控制器在10 ms左右即可控制住故障，采樣長度N分別為1，5，10，采樣間隔Δ為0.01 s,協方差陣R=202,將歷史緩沖區取NΔ對應值，分別為0.01，0.05，0.1 s，仿真結果如圖5、圖6所示。

由圖5、圖6可以看出，采樣長度N越大，故障估計值f恢復正常的拍數越少，越不利于觀測到故障；采樣長度過小，故障估計值f有較大損失。為了保證故障檢測的及時性及準確性，采樣長度為5較為合適，實際應用中可根據此分析方法確定實際采樣長度。

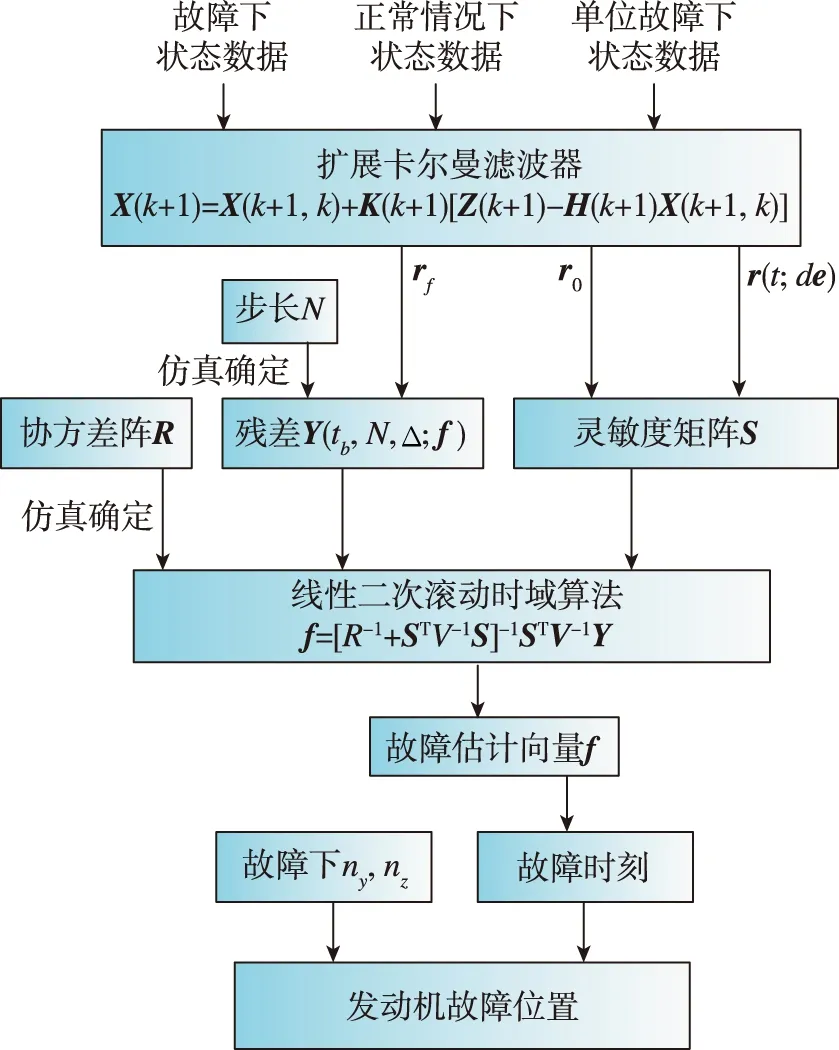
圖4 估算算法流程圖Fig.4 Flow chart of estimation algorithm

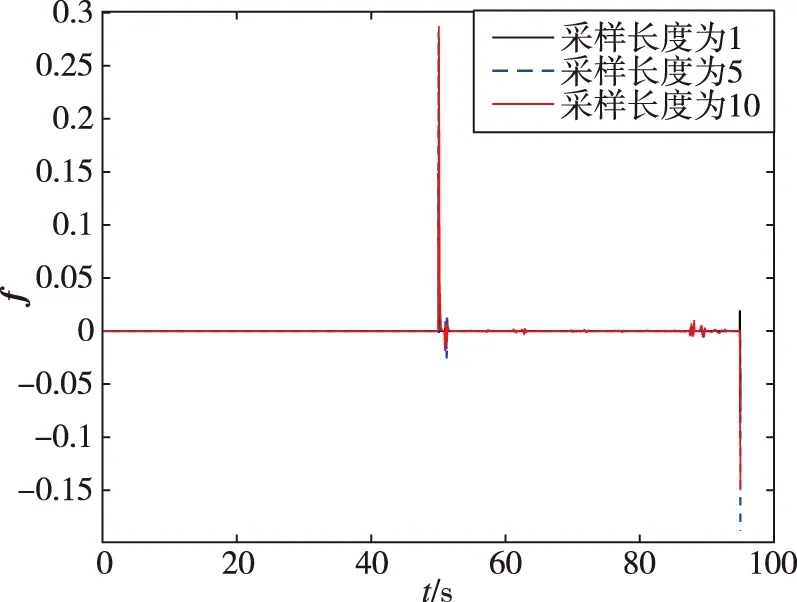
圖5 不同采樣長度下故障檢測結果Fig.5 Fault detection results under different sampling lengths

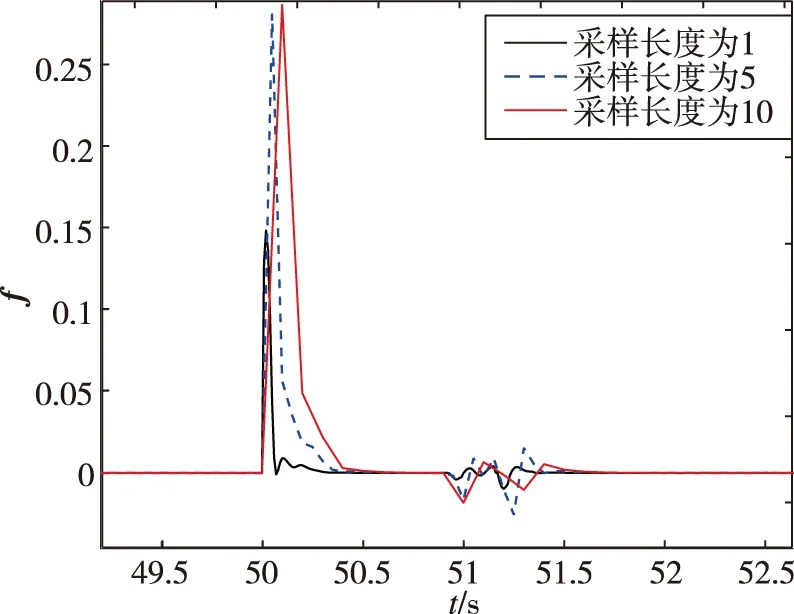
圖6 不同采樣長度下故障檢測結果放大圖Fig.6 Enlarged view of fault detection results under different sampling lengths

(2)不同故障協方差矩陣R對仿真結果的影響

設定50 s時發生50%的推力下降，采樣長度N為5，采樣間隔Δ為0.01 s,協方差陣R分別為0.012，12，202，5002，5 0002，10 0002,歷史緩沖區為0.05 s，圖7給出50 s附近故障估計結果。

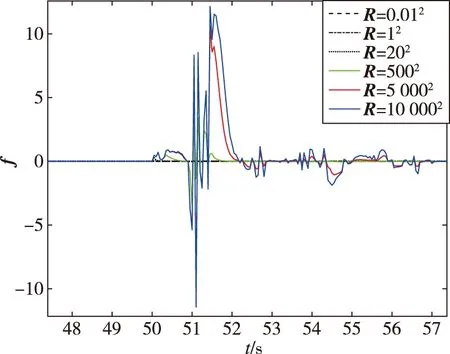
圖7 50 s附近不同協方差陣下的故障估計結果(大范圍)Fig.7 Fault detection results under different covariance matrices around 50 s(wide range)

由圖7可以看出，協方差陣取得越大，f反映故障發生強度越顯著，但取得過大f會出現二次增大，可能導致故障檢測的誤報。根據上述結果進一步確定合適的協方差陣大小，協方差陣R分別為12，52，202，502，1002,仿真結果如圖8所示。

圖8 50 s附近不同協方差陣下的故障估計結果(小范圍)Fig.8 Fault detection estimation results under different covariance matrices around 50 s(small scale)

考慮到故障檢測的準確度，避免二次誤報，因此選取R=202至502量級較為合適。

(3)不同推力下降程度仿真

基于上述仿真，給出同一時刻(20 s)下，推力下降故障分別為0%、30%、50%時的仿真結果，取采樣長度N=5，采樣間隔Δ為0.01 s,協方差陣R=202,將前0.05 s數據作為歷史緩沖區，故障殘差仿真結果如圖9、圖10所示，故障向量f的估計如圖11所示。

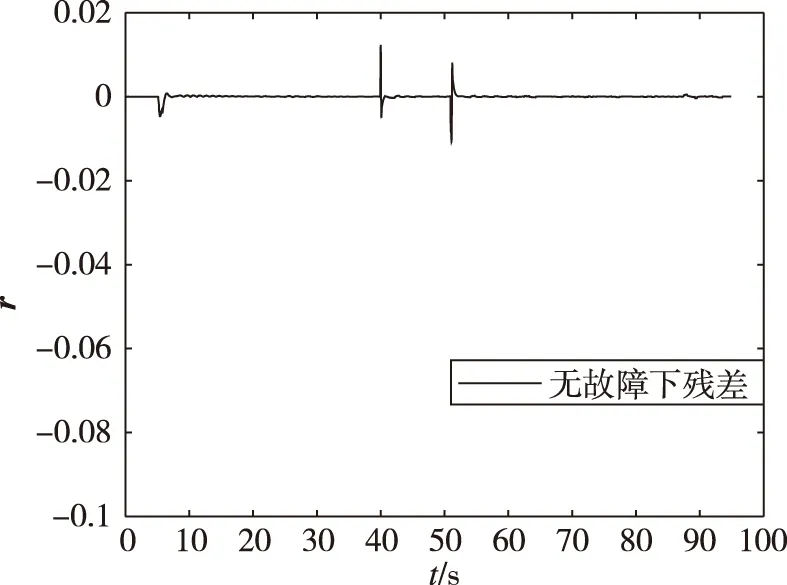
(a) 無故障

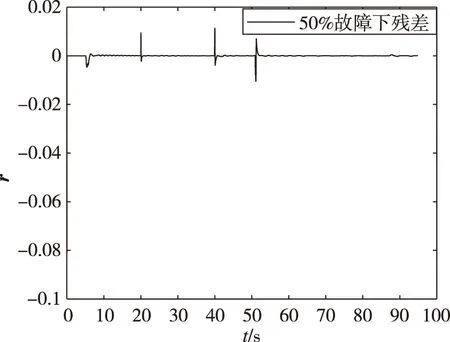
(c) 50%故障圖9 20 s時刻不同故障程度殘差仿真結果Fig.9 Simulation results of residuals with different fault degrees at 20 s

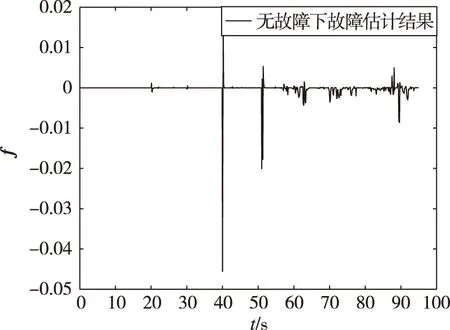
(a) 無故障

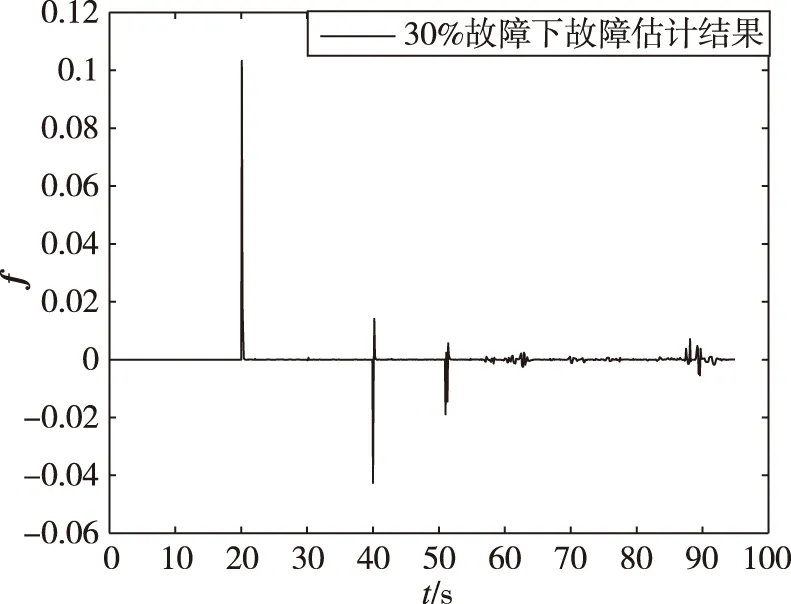
(b) 30%故障

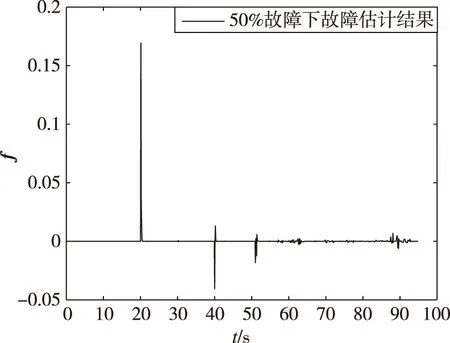
(c) 50%故障圖10 20 s時刻不同故障程度故障檢測仿真結果Fig.10 Simulation results of fault detection with different fault degrees at 20 s

由上述結果可得，同一時刻發生不同故障程度，f估計值不同。在20 s時刻，以5%故障下降程度為間隔，仿真獲取故障時刻估計的峰值為fmax，繪制曲線如圖11所示，可以判斷兩者存在近似的線性關系。

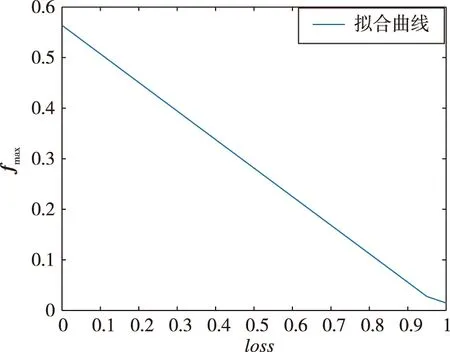
圖11 故障程度與故障估計值f關系Fig.11 Relationship between fault degree and fault estiomate f

由圖11可以看出,兩者之間存在線性關系，由于該曲線僅針對50 s時刻故障，遍歷時間與故障程度，形成一個二維表格，根據辨識結果在表格內進行插值，即可得到推力下降程度。

以推力下降程度lossP為因變量、f估計峰值為自變量進行線性擬合，可得到20 s時刻下估計值f與實際推力下降程度lossP關系式

(27)

利用上式將故障估計值與預設的故障程度對應，表1給出部分驗證結果。

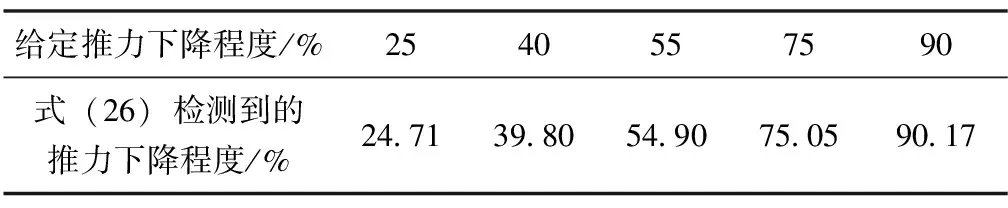
表1 故障程度的估計結果

上述結果表明，該方法能夠較為準確地獲得故障損失程度。在檢測出故障后，由于控制器的控制作用，所以突變恢復正常。殘差曲線中40，50 s附近也產生了與推力下降故障不相關的突變。由表1可以看出，這些突變造成的f估計值的變化遠小于推力下降故障造成的估計結果的變化，表明該方法對推力下降故障具有較高的靈敏度。

3.2 4臺發動機故障檢測

基于過載在故障時刻突變方向與發動機位置相關的思路進行多次故障檢測驗證，結果如表2所示。

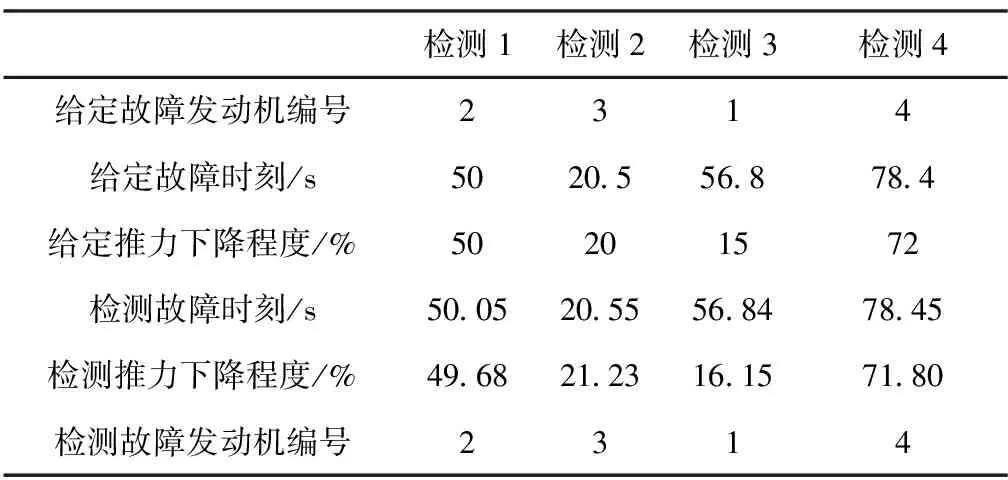
表2 故障發動機編號檢測

上述結果表明，利用根據ny,nz的突變方向能夠準確判定發動機故障臺的編號,表明該思路能夠用于4臺發動機的故障定位。

4 結論

本文針對運載火箭動力系統的推力下降故障，提出了一種線性二次滾動時域算法用于估計故障時間與故障程度，結合估計算法檢測的故障時間提出一種故障定位的策略。仿真結果表明，該方法能夠成功檢測發動機故障，并對該類型故障具有較高靈敏度。

此外，給出根據過載的突變方向定位故障的策略，與估計算法檢測的故障時間相結合，實現了發動機故障的準確定位。