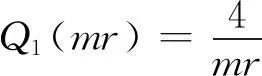頻率和收發距廣普適用的均勻層狀介質電磁場直接積分算法

戴世坤 曾 鈴* 周印明③ 李 昆 陳輕蕊 凌嘉宣

(①中南大學地球科學與信息物理學院,湖南長沙 410083; ②中南大學有色金屬成礦預測與地質環境監測教育部重點實驗室，湖南長沙 410083； ③東方地球物理公司綜合物化探處，河北涿州 072751)

0 引言

在電磁場地球物理方法中，均勻層狀介質電磁場解析表達式含有漢克爾積分[1-2]，其核函數為0階和1階Bessel函數。隨著其宗量的增大，Bessel函數呈現快速振蕩和慢衰減的特征，造成漢克爾積分難以實現高效、高精度的計算，特別是高頻和大收發距情況下難度更大。為了解決這個問題，學者們提出了許多方法，主要分為兩大類： 第一類為數字濾波方法； 第二類為直接積分法(Direct integration method，DIM)。Ghosh[3]首先將數字濾波法引入地球物理數值計算； 針對電磁法，Johansen等[4]提出了漢克爾數字濾波系數的解析計算方法。之后，很多研究者給出了不同優化濾波系數[5-6]。蔡盛[7]對比了5組高精度快速漢克爾長濾波系數的計算精度，研究結果表明在一定的收發距和頻率范圍內，計算精度較高，但耗時太大，隨著濾波系數的增大而增長。總體來說，數字濾波法適用于中、低頻和適中的收發距情況，在高頻和大收發距的情況下計算精度很低。考慮到數字濾波法的局限性，眾多學者利用多項式精確擬合核函數的思想，達到求解解析解的目的，提出了直接積分類方法。代表性方法包括高斯積分法[8]、基于快速正弦余弦算法的漢克爾變換算法[9]、直接法[10]、離散復鏡像法[11-12]、譜域法[13]、基于高階窗函數的結合非線性變換的算法[14]、外推積分方法(QWE)[15]、三次樣條插值法[16]等。其中最后一種方法采用三次樣條函數對核函數進行插值，得到一系列核函數為多項式的簡單Sommerfeld積分，再利用Bessel函數的遞推公式和Lommel公式的漸進展開求解。這些方法雖能較好地應用于低頻和適中收發距的均勻層狀介質電磁場的計算，但隨著頻率和收發距的增大，這些方法的計算精度逐漸降低，甚至失效。針對高頻電磁場的計算，鄭圣談等[17]提出了高密度采樣數字濾波法，但當介質導電率變小、介電常數變大、收發距變大、頻率增加時，該方法計算精度會大幅度降低，不具普適性。

針對電磁場漢克爾積分核函數復雜的特點，本文提出一種高效、高精度直接積分方法，用于頻率和收發距廣普適用的電磁場高效、高精度的數值計算。其基本思想是Bessel函數可以在兩個區間分別用不同的多項式展開，每一區間的漢克爾積分可離散為多個單元積分之和，每個單元被積函數采用三次樣條插值函數表示，由此可求得積分的解析解，并通過求和獲得漢克爾積分的數值解。在此基礎上，利用均勻全空間電偶極子電磁場的解析解，正確選取積分范圍，并合理剖分積分單元。數值解與解析解對比表明，本文算法正確、可靠。與數字濾波類算法的比較表明，本文算法廣泛適用于不同頻率和不同收發距電磁場的計算，具有較強的普適性。

1 方法原理

均勻層狀介質電磁場的解析解可用漢克爾積分表示

(1)

式中：g(m)為大地響應函數，m表示積分參數；r為發射源到接收點的水平距離，mr為宗量；Jn(·)為n階Bessel函數。

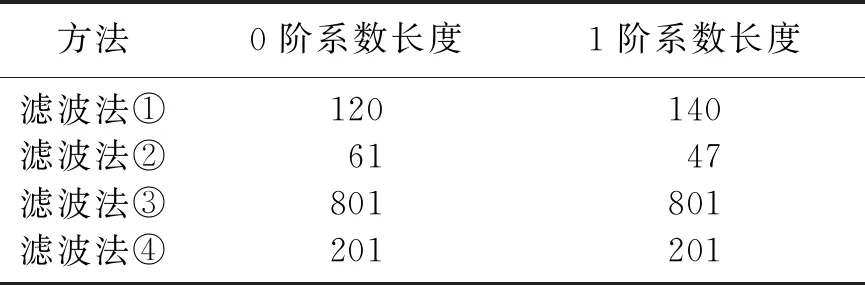
式(1)中，Bessel函數為0階和1階，根據特殊函數手冊[18]，可以分別在兩個區間用不同的多項式展開。第一區間為0≤mr≤4，Bessel函數可展開為簡單的代數多項式，每個積分單元內代數多項式與響應函數的乘積可用三次樣條插值函數表示。第二區間為4

在第一個區間(0≤mr≤4)有

J0(mr)=-0.0005014415t7+0.0076771853t6-

0.0709253492t5+0.4443584263t4-

1.7777560599t3+3.9999973021t2-

3.9999998721t+1.0+e0(mr)

(2)

式中截斷誤差e0≤1×10-8。

在第二個區間(4

(3)

式中

(4)

其中截斷誤差e1、e2≤1×10-8。

對第一區間0≤mr≤4，將積分范圍均勻剖分為N個單元。由式(2)可知，Bessel函數的展開式為簡單的代數多項式，因此設f(m)=g(m)J0(mr)，這個區間的積分F1可表示為

(5)

式中mi(i=1,2,…,N,N+1)為離散采樣點。每個單元內被積函數fi用三次樣條插值函數[18-19]表示為

fi=di(m-mi)3+ci(m-mi)2+

bi(m-mi)+ai

(6)

式中ai、bi、ci、di為單元i的三次樣條插值函數的系數。設Li=mi+1-mi為單元i的長度，單元i的積分解析表達式為

(7)

因此，第一區間各單元積分累加的結果為

(8)

對于第二區間4

(9)

設

(10)

(11)

(12)

式中

(13)

因此，第二區間各單元積分累加求和結果為

(14)

最終漢克爾積分為

F=F1+F2

(15)

2 積分參數的選取

為了提高計算精度和效率，需合理選取積分范圍，恰當地進行單元剖分，而這些參數的選取依賴于響應函數的特征和變化規律[19-20]。本文以均勻全空間電偶極子源電磁場為例，通過研究不同響應函數的變化規律，確定積分范圍，并選定單元剖分方案。

在均勻全空間中，將x方向上電偶極子源產生的電、磁場用漢克爾積分表示，其解析解的漢克爾積分表達式分別為

(16a)

(17)

(18)

取電導率σ=0.0001S/m，相對介電常數ε=1，電偶極子源中心坐標為(0,0,0)，偶極矩為1C·m，頻率v=1×108Hz， 積分變量m在[1×10-12,1×108]區間按對數等間距均勻采樣，每一個對數單位內采樣點為5000個。計算上述三種響應函數的值，結果如圖1所示。

圖1 三種響應函數隨m的變化曲線

由圖1可以看出，m從1×10-6增大到1×10-1時，三種響應函數的對數值呈線性增大； 當m為1×10-1～1×101時，三種響應函數值隨m變化較快，尤其在1×100附近出現尖脈沖；m>102時三種響應函數隨著m的增大按照對數以近似線性規律迅速衰減； 在m接近1×103時，三種函數的值均衰減至低于10-20。根據上述分析結果，m的積分范圍可選取為[0,1×104]，并整體上按照對數等間距規律進行單元剖分。特別地，在m為1×10-1～1×102時，因響應函數值變化較快，單元剖分可適當加密，尤其在m接近1×100時，響應函數變化劇烈，單元剖分需格外加密。

根據以上原則，對均勻全空間電偶極子源產生電磁場用漢克爾積分表達式進行數值計算，并與解析解進行比較，以驗證算法的正確性。下文分別計算均勻全空間中1×104、1×108Hz的電場響應。

對v=1×104Hz，計算zr=40m所在平面的電磁場，計算范圍：x方向為-500～500m，y方向為-500～500m，m的采樣區間為0～1×104。在區間1×10-3～1×101加密積分單元，總采樣點數為373。圖2為電場分量的數值解、解析解及相對誤差平面圖。由圖可見，數值解與解析解曲線形態基本一致，相對誤差都很小，最大為8×10-6(Ex分量)，即便在源附近，其誤差也不大于1%，表明本文算法的正確性和可靠性，且精度較高。

圖2 v=1×104Hz時電場分量Ex(a)、Ey(b)、Ez(c)的解析解(左)、數值解(中)及其相對誤差(右)

對v=1×108Hz，計算zr=10m所在平面的電場。計算的平面范圍x方向為-15～15m，y方向為-15～15m，m的采樣區間為0～1×105，在區間1×10-2～1×100加密采樣點，總采樣點數為811。圖3為該模型的電場分量數值解、解析解及相對誤差平面圖。從圖3可看出，數值解與解析解曲線形態基本一致，相對誤差很小，其中Ey分量的誤差最大，最大為4×10-6，即便如此，在源附近的誤差也都不大于1%，這表明算法在高頻時計算的場值是正確、可靠的，且精度較高。

圖3 v=1×108Hz時電場分量Ex(a)、Ey(b)、Ez(c)的解析解(左)、數值解(中)及其相對誤差(右)

上述兩個頻率的計算結果證明了本文算法正確、可靠，且能適應高頻電磁場的計算。

3 模型算例

設計均勻全空間模型和均勻層狀介質模型，分別使用本文DIM算法和常用的數字濾波類算法模擬電磁場，以驗證本文算法對不同頻率、不同收發距電磁場模擬計算的廣普適用性。

3.1 均勻全空間模型

首先驗證本文算法對于頻率的廣普適用性。

在均勻全空間中，設發射源到接收點的水平距離R=100m，計算頻率范圍為1×10-2～1×1010Hz，電導率σ=0.0001S/m，相對介電常數ε=1，電偶極子源中心坐標為(0,0,0)，偶極矩為1C·m。分別使用本文算法與四種經典的數字濾波算法計算該模型的數值解與解析解的相對誤差，其中四種數字濾波算法的濾波系數選取見表1。數字濾波方法①和②參見文獻[21]，方法③和方法④分別參見文獻[22]和文獻[23]。這四種方法及本文提出的直接積分法計算結果如圖4所示，其中黑色直線表示相對誤差為1%。從圖4可看出，在頻率v<1×106Hz的情況下，這四種數字濾波類算法的計算誤差均小于1%；隨著頻率的升高，四種濾波系數類算法的誤差越來越大，而本文直接積分法的計算誤差小于1%。表明本文提出的直接積分法計算精度高，在廣泛的頻率范圍內適用。

表1 四種常用的數字濾波算法的濾波系數長度取值

為驗證該方法對收發距的廣普適用性，在均勻全空間中，取頻率v=1×107Hz， 發射源到接收點的水平距離r范圍為1×10-3～1×103m，其他參數不變。使用本文算法與四種經典的數字濾波算法分別計算不同收發距時的數值解與解析解的相對誤差，其中四種數字濾波算法的濾波系數選取同上(表1)。計算結果見圖5。可以看出，在收發距r<2m時，直接積分法和四種數字濾波類算法的計算誤差均小于1%； 但隨著收發距的增大，四種濾波系數類算法的誤差越來越大，而直接積分法在任意r時，計算誤差均不大于1%。表明本文提出的直接積分法計算精度高，在廣泛的收發距范圍內適用。

圖4 均勻全空間模型不同頻率下直接積分法與四種

圖5 均勻全空間模型不同收發距下直接積分法與四種

3.2 層狀介質模型電磁場不同算法對比

設計一個三層層狀介質模型，模型參數見圖6。電偶極子源中心坐標為(0,0,0)，偶極矩為1C·m。

圖6 三層層狀模型斷面示意圖

計算頻率v=1×108Hz、z=10m所在平面的電場分量，計算平面范圍x方向和y方向均為-15～15m。

圖7和圖8分別為表1中第④種數字濾波法與本文直接積分法計算的Ex、Ey、Ez實部與虛部平面等值線圖。由圖可見，數字濾波法計算的Ex、Ey、Ez等值線圓滑度較低，表明計算結果有一定誤差，而直接積分算法計算的電場等值線圓滑度較高，表明計算結果更準確、精度更高。

圖7 三層層狀介質模型直接積分法(上)與數字濾波法(下)計算的電場分量Ex(a)、Ey(b)和Ez(c)實部平面等值線圖

圖8 三層層狀介質模型直接積分法(上)與數字濾波法(下)計算的電場分量Ex(a)、Ey(b)和Ez(c)虛部平面等值線圖

4 結論

本文提出一種高效、高精度的直接積分方法，適用于不同頻率和不同收發距的電磁場模擬計算，尤其適合高頻電磁場的計算，具體取得以下結論。

(1)利用Bessel函數可以在兩個積分區間分別用不同的多項式展開。將每一區間的漢克爾積分離散成多個單元積分之和，每個單元被積函數采用三次樣條插值函數表示，由此可求得積分的解析解。通過疊加，求得漢克爾積分的數值解。

(2)響應函數的特征和變化規律是積分參數選取的關鍵因素。為此，以均勻全空間電偶極子源電磁場為例，研究了三種典型的響應函數隨積分變量的變化規律。計算結果表明，三種響應函數隨積分變量呈對數規律變化，據此按對數規律確定積分范圍和單元剖分：在響應函數值變化快的地方，單元剖分可適當加密，尤其在尖脈沖附近，單元剖分需格外加密；在響應函數值變化慢的地方，單元剖分可適當稀疏。這樣合理剖分積分單元可提高直接積分法的計算精度和效率。均勻全空間電偶極子源電磁場數值解與解析解對比表明本文算法更正確、可靠。

(3)分別設計均勻全空間模型和層狀介質模型，對本文提出的直接積分法與數字濾波方法電磁場數值計算結果進行對比，結果表明本文積分法對頻率和收發距具有廣普適用性，尤其對高頻電磁場，其優勢更加突出，為高頻電磁場的計算提供了重要的方法基礎。

附錄A 1階Bessel函數漢克爾積分的解析表達式推導過程

根據特殊函數手冊[18]，對J1(mr)函數分兩個區間進行展開。

在第一個區間(0≤mr≤4)

0.0236616773t5+0.1777582922t4-

0.8888839648t3+2.6666660544t2-

3.9999999710t+1.9999999998)+e0(mr)

(A-1)

其中截斷誤差e0≤1×10-8。

在第二個區間(4

(A-2)

式中

(A-3)

0.000999941t-3+0.000266891t-2-

0.001601836t-1+0.093749994)+e2(mr)

(A-4)

其中截斷誤差e1、e2≤1×10-8。

對于第一區間(0≤mr≤4)，將其剖分為N個單元，由式(A-2)可知，Bessel函數的展開式為簡單的代數多項式，因此設f(m)=g(m)J1(mr)，這部分的積分為

(A-5)

設mi(i=1,2,…,N,N+1)為離散采樣點，每個單元內被積函數fi可采用三次樣條插值函數表示為

fi=di(m-mi)3+ci(m-mi)2+

bi(m-mi)+ai

(A-6)

(A-7)

第一區間各單元積分累加表達式為

(A-8)

對第二區間(4

(A-9)

設

(A-10)

在每個單元內，Fp、Fq變化規律簡單，可采用三次樣條插值函數近似表示為

(A-11)

(A-12)

式中

(A-13)

可求得第二區間各單元的積分為

(A-14)

據此，漢克爾積分為

F=F1+F2

(A-15)