抓住立體圖形展開中的不變量

劉護靈

在歷屆高考的立體幾何問題中折疊與展開問題現在已經是常考的知識點之一，也是競賽和高考對立體幾何考查的熱點問題，是考察考生空間想象能力與創新能力的良好素材. 它們的相互轉變正是空間幾何與平面幾何問題轉化的集中體現. 對于圖形的翻折與展開問題的關鍵在于畫好折疊與展開前后的平面圖形與立體圖形，并弄清折疊與展開前后哪些發生了變化，哪些沒有發生變化. 這些未變化的已知條件都是我們分析問題和解決問題的依據. 下面我們分析2020年高考理科1卷的第16題.

一、原題呈現

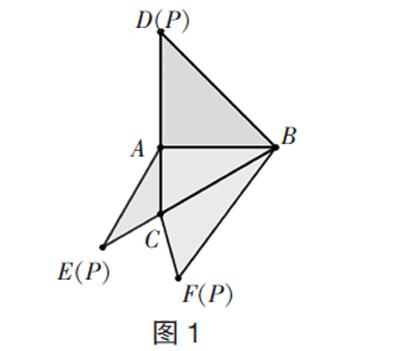
16. 如圖1，在三棱錐P-ABC的平面展開圖中，AC=1，AB=AD= ，AB⊥AC，AB⊥AD，∠CAE=30°，則cos∠FCB =__________.

二、解析過程

由平面展開圖可知，在等腰Rt？駐DAB中，

BD= AB= ，

∵ D，E，F重合一點P，（這是本題關鍵的一個信息點）

說明什么呢？

說明了BF=BD，AE=AD，CE=CF！

即得到：

∴ AE=AD= ，BF=BD= ，

下一步需要在？駐ACE，把CE給求出來，即：

在？駐ACE中，由余弦定理，得：

CE2=AC2+AE2-2AC·AE·cos∠CAE=12+（ ）2-2×1× × =1，

∴ CE=CF=1，

最后一步，在？駐BCF中利用可求出答案，即：

在？駐BCF中，由余弦定理，得：

cos∠CAE= · =- .

解題反思1：2020年高考命題體現高考考綱修改的基本原則：“堅持整體穩定，推進改革創新，優化考試內容，著力提高質量，提前謀篇布局，體現素養導向”中，并將“整體穩定”放在首位. 試題考點比較常規，難度有所降低，題型分布回歸常態. 注重對數學核心素養的考查，體現素養導向.

解題反思2：此16 題看起來考查的是解三角形，但考生比較難還原圖形中的邊長信息，所以實質還考查考生的空間想象能力、閱讀能力. 據有關調查結果表明，大多數的老師平常上課的時候只是用板書、拿卷子講課，很少用計算機等多媒體設備，這不利于學生們培養三維立體感.

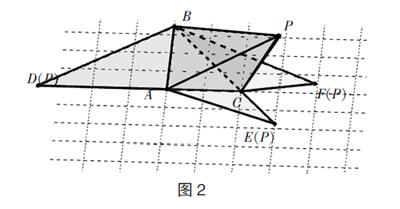
此題利用數學繪圖軟件geogebra軟件制作的立體圖形如下：

還可以拖動滑動條，生動形象的演示展開的過程，有利于培養空間想象能力.

三、變式練習

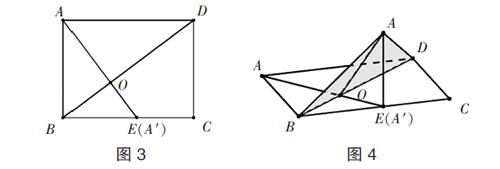
矩形ABCD，AB=3，BC=4，沿對角線BD把△ABD折起，使點A在平面BCD上的射影A′落在BC上，求二面角A—BD—C的平面角的余弦值大小.

【解析】這是一道由平面圖形折疊成立體圖形的問題，解決問題的關鍵在于搞清折疊前后“變”與“不變”.

在平面圖形中過A作AE⊥BD交BD于O，交BC于E，則折疊后OA、OE與BD的垂直關系不變.

OA與OE此時變成相交兩線段并確定一個平面AOE，此平面必與棱BD垂直.

由此可知，平面AOE與平面ABD、平面CBD的交線OA與OE所成的角，即∠AOE，為所求二面角的平面角.

另外，A在平面BCD上的射影A′必在OE所在的直線上，又由題設射影A′落在BC上，所以E點就是A′，這樣的定位給下面的定量計算提供了幫助.

如圖5，在Rt？駐AOB中，AO=AB· =3× = ，OA′=OE=BO·tan∠CBD，而BO= = ，tan∠CBD= ，故OA′= . 在Rt？駐AA′O中，∠AA′O=90°，所以cos∠AOA′= = .

四、同類高考題演練

1. 圖6是由矩形ADEB，Rt？駐ABC和菱形BFGC組成的一個平面圖形，其中AB=1，BE=BF=2，∠FBC=60°，將其沿AB，BC折起使得BE與BF重合，連結DG，如圖7.

（1）證明：圖7中的A，C，G，D四點共面，且平面ABC⊥平面BCGE;

（2）求圖7中的二面角B-CG-A的大小.

【分析】（1）因為折紙和粘合不改變矩形ABED，Rt？駐ABC和菱形BFGC內部的夾角，所以AD∥BE，BF∥CG依然成立，又因E和F粘在一起，所以得證. 因為AB是平面BCGE垂線，所以易證.

（2）在圖中找到B-CG-A對應的平面角，再求此平面角即可. 于是考慮B關于GC的垂線，發現此垂足與A的連線也垂直于CG. 按照此思路即證.

【解析】（1）證：∵ AD∥BE，BF∥CG，又因為E和F粘在一起.

∴ AD∥CG，A，C，G，D四點共面.

又∵ AB⊥BE，AB⊥BC，

∴? AB⊥平面BCGE，∵ AB？奐平面ABC，∴平面ABC⊥平面BCGE，得證.

（2）過B作BH⊥GC延長線于H，連結AH，因為AB⊥平面BCGE，所以AB⊥GC，而又BH⊥GC，故GC⊥平面HAB，所以AH⊥GC. 又因為BH⊥GC所以∠BHA是二面角B-CG-A的平面角，而在△BHC中，∠BHC=90°，又因為∠FBC=60°，故∠BCH=60°，所以BH=BCsin60°= .

而在△ABH中∠ABH=90°，tan∠BHA= = = ，即二面角B-CG-A的度數為30°.

解題反思3：此題建系也可以計算，這里給出的是不建系的方法. 此題在當年是比較新穎的立體幾何考題. 首先是多面體粘合問題，考查考生在粘合過程中哪些量是不變的. 再者粘合后的多面體不是直棱柱，建系的向量解法在本題中略顯麻煩，突出考查幾何方法. 最后將求二面角轉化為求二面角的平面角問題，考查考生的空間想象能力.

2. 一個正方體的平面展開圖及該正方體的直觀圖的示意圖如圖9所示，在正方體中，設BC的中點為M，GH的中點為N.

（1）請將字母F，G，H標記在正方體相應的頂點處（不需說明理由）;

（2）證明：直線MN∥平面BDH;

（3）求二面角A-EG-M的余弦值.

【解析】（1）點F，G，H的位置如圖10所示.

（2）證明：連接AC，BD交于點O，連接OH，OM.

因為M，N分別是BC，GH的中點，

所以OM∥CD，且OM= CD，HN∥CD，且HN= CD，

所以OM∥HN，OM=HN，

所以四邊形MNHO是平行四邊形，

從而MN∥OH.

又MN？埭平面BDH，OH？奐平面BDH，

所以MN∥平面BDH.

（3）方法一：過M作MP⊥AC于P. 在正方體ABCD-EFGH中，AC∥EG，所以MP⊥EG.

過P作PK⊥EG于K，連接KM，所以EG⊥平面PKM，

從而KM⊥EG，所以∠PKM是二面角A-EG-M的平面角.

設AD=2，則CM=1，PK=2.

在Rt△CMP中，PM=CMsin 45°= .

在Rt△PKM中，KM= = .

所以cos∠PKM= = ，即二面角A-EG-M的余弦值為 .

方法二：如圖11，以D為坐標原點，分別以 ， ， 方向為x軸，y軸，z軸的正方向，建立空間直角坐標系D-xyz.

設AD=2， 則M（1， 2， 0）， G（0， 2， 2）， E（2， 0， 2）， O（1， 1， 0），

所以 =（2， -2， 0）， =（-1， 0， 2）.

設平面EGM的一個法向量為 =（x， y， z），

由 · =0， · =0，得2x-2y=0，-x+2z=0，取x=2，得 =（2， 2， 1）.

在正方體ABCD-EFGH中，DO⊥平面AEGC，

則可取平面AEG的一個法向量為 = =（1， 1， 0），

所以cos〈 ，? 〉= = = ，

故二面角A-EG-M的余弦值為 .

小結：平面圖形通過折疊變為立體圖形，立體圖形通過展開變成平面圖形，在圖形發生變化的過程中，折疊或展開前后有些量（長度、角度等）沒有發生變化，我們稱其為“不變量”. 這些不變的線線關系，尤其是平面圖形中的線線平行、線線垂直關系是證明空間平行、垂直關系的起點和重要依據;不變的數量關系是求解幾何體的數字特征，如幾何體的表面積、體積、空間中的角與距離等的重要依據.

責任編輯 徐國堅