淺談如何在分數學習中培養小學生“數形結合”思維方式

胡俊

摘 要：“數形結合”是數學學習中非常重要的一種思維方式，是至關重要的教學手段。掌握好“數形結合”的方法與思想，能夠很好地幫助學生構建數學模型。小學階段分數方面的知識內容較為抽象，學生利用“數形結合”思維方式，能夠有效地理解分數之間的關系，并突破學習中諸多難點。文章將就如何在分數教學中培養小學生的“數形結合”思維方式進行分析，以期為小學數學教學提供理論參考。

關鍵詞：分數教學;數形結合;思維方式

中圖分類號：G623.5 文獻標識碼：A 收稿日期：2020-05-19 文章編號：1674-120X（2020）28-0049-02

一、培養小學生“數形結合”思維方式的原因

數學是以數與形為基礎對象的學科，一切數學問題都是圍繞數與形的演變、發展而展開的。“數形結合” 就是根據數量與圖形之間的對應關系把抽象的數學語言與直觀的圖形相結合，使抽象思維和形象思維相結合，是一種常用的數學方法。在數學發展進程中，數與形于內容上互相聯系，于方法上互相滲透，彼此間在一定的條件下互相轉化。小學生的思維正處于由具體形象思維向抽象邏輯思維過渡的時期，而抽象邏輯思維仍具有很強的具體形象性。

例如，在教學分數大小比較的內容時，教師如果干巴巴地講解二分之一大于三分之一，學生可能并不能夠理解。因為在學生的認知里二小于三，可是在分數中二分之一大于三分之一。

例如，在講解分數時，教師采用講故事的方法：“豬八戒分西瓜。豬八戒剛咬第一口，悟空就從天而降。孫悟空說：‘我吃西瓜的二分之一。八戒心里一直想多吃點，聽了高興極了，說：‘我可要吃八分之一。。”學生這時候就議論紛紛了，到底誰吃得多呢？如果沒有“數形結合”，學生就不能夠準確地理解到底誰吃得多。

因此，在分數的教學中，教師可利用圖形來表示具體的量，然后根據圖形間彼此的關系，適當地提出合理的分析與解釋，有效地突破教學中的重難點問題。學生運用“數形結合”的思維方式進行分數學習，就是非常有效的學習方法。

二、培養學生“數形結合”思維方式的作用

“分數”對小學生來講是一個比較抽象的概念，教師在教學實踐中，要淡化分數的表現形式，注重分數的實質，以學生能力的發展為本，以解決問題為中心，以引導學生發現問題、分析問題、解決問題的邏輯性來體現教學的嚴謹性。

（一）運用“數形結合”思維，理解分數意義

教學中“分數”與“圖形”共同滲透，讓學生見“分數”就想到利用“圖形”來分析和理解分數的實質，見“圖形”就想到背后“分數”的意義和相關運算。

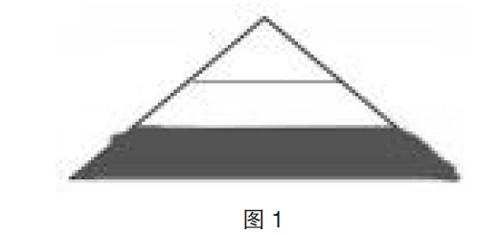
例如，北師大版教材三年級數學“分一分（二）”這一課著重研究“多個物體的幾分之幾”的分數意義。在開課時，教師出示圖1：用下邊的分數表示涂色部分對嗎？為什么？以此來復習“平均分”。學生形象直觀地看出圖形中每份的大小不同，體驗什么叫作平均分，以及平均分在分數中的重要作用，從而有效地掌握這一知識要點。

（二）運用“數形結合”思維，講解異分母分數加減法

異分母分數加減法，對學生來說難點就是異分母，而“通分”這一概念有些抽象，在理解上有難度，所以有必要幫助學生構建分母相同概念，而且在理解相同單位“1”的基礎上，分數才能進行加減法，這是異分母分數加減法的前提。利用“數形結合”的思想和方式，學生通過直觀的圖形，先把單位“1”平均分，然后進行通分，這一步驟是解決異分母分數加減法的關鍵和突破口。

例如：課本在設計上采用了圖2的數形結合的方法，很好地體現了-，+先通分后計算的必要性，進一步借助面積模型的直觀運算和通分的聯系，結合方格圖來說明各自思考的過程，以幫助學生在學習中，特別是在直觀運算中，加深對異分母分數加減法算理的理解。

（三）運用“數形結合”思維，理解分數算理

分數乘除法教學的主要特點一是注重從不同的問題情境，引導學生多角度理解分數乘除法的意義;二是注重實踐操作和各種直觀模型的運用，讓學生在自主探究中獲得分數乘除法的計算方法。在教學過程中，教師要注重實踐操作和直觀比較相結合的教學方法，發展學生利用圖形語言表示數量關系的思維能力，培養學生數形結合的數學思想。通過面積模型與線段圖等直觀數學建模，從不同角度理解分數乘除法的算理意義和計算方法，豐富學生的數學體驗和學習經驗。

1.分數乘法中，數形結合的合理運用

利用方格圖，幫助學生理解分數與整數、分數與分數的關系，解決學習中的困難。

例如：8×表示什么意思？畫一畫，算一算。教材第25頁在設計上，給出一列方格（如圖3），讓學生經歷多種方法嘗試表示8×的過程，既鍛煉了學生數形結合的思想，又讓學生體驗表示方法的多樣性，還能清楚地理解8×的算理。

2.分數除法中，數形結合幫助理解“量率對應”

在學習分數除法的意義和計算方法時，教材借助整數除法的意義，可以直觀幫助學生理解除以一個非零的數，等于乘這個數的倒數。教材中設計了基于面積模型的活動，以讓學生利用長方形的面積模型、線段圖等直觀圖形，理解其中的算理和意義。特別在“量率對應‘求單位1”的處理環節中，借助直觀的圖形，能夠有效地理清問題中的數量關系。而在教學中，教會學生這一重要技能，能夠培養學生良好的數學修養，為后續學習的數學建模提供必要的技能支撐。

例如：某學校有故事書150本，故事書比科技書的本數多，科技書有多少本？（如圖4）在解決這道題的過程中，首先，學生要找到單位“1”;其次，借助圖形中的“故事書”與“科技書”的數量關系;再次，根據“量率對應”求出單位“1”對應的量。在解題過程中，學生可以通過數量關系直接求解，也可以根據圖形的直觀比較，利用方程解決問題。

小學數學中，有相當一部分的內容是計算問題。算理是抽象的、難理解的，如何把它簡單地呈現出來，數形結合很重要。教師應以清晰的理論指導學生理解算理、掌握計算方法，正所謂“知其然，知其所以然”。

在分數除法這節課中，怎樣讓學生理解一個分數除以一個整數就等于這個分數乘以這個整數的倒數呢？比如，把一張紙的平均分成2份，每一份是這張長方形紙的幾分之幾呢？首先，讓學生將一張紙平均分為5份，然后涂上4份的顏色，用來表示。展示圖為：

然后，將這幅圖的平均分為2份，再涂上顏色，如圖所示：

每一份的的，使用計算公式表示為：×=

=。學生明白事實上就是乘以2的倒數。在教學第二道題目的時候：將一張紙的平均分為3份，每一份是這一張長方形紙的幾分之幾呢？學生很快明白了計算的道理，每一份就是的，也就是×=。這樣結合圖形開展教學活動，然后指導學生歸納正確的計算法則，讓學生親自經歷、感受數形結合的整個過程。在圖象的支持下，學生能夠更好地理解算理。

（四）運用“數形結合”思維，幫助學生理解數量關系

數形結合應該全面貫穿整個小學時期，解決數學教學難題。通過數形結合的方式，表現出比較具體的、直觀的數學符號，有助于分析題目中的數量關系，快速找到解決問題的辦法，提升學生分析問題、解決問題的能力。

比如，應用題：根據科學規定，成人身體里面的水分占到人體體重的，然而兒童身體中的水分占身體體重的，小紅身體中的水分重28千克，小紅的體重是多少呢？

學生理解圖片中的實際意義就是：小紅體重的是小紅

身體中水分的重量，進而列出數量的關系式為：小紅體重×=水分的重量，然后得出方程式。解：設小紅體重是x千克，那么×x=28。這樣的話就等于將抽象思維轉變成為直觀思維來解決問題。

三、結語

堅持數形結合是很有必要的，這是尊重學生客觀認知規律的。發展學生直觀與抽象思維相結合的能力，提高學生的直觀形象學科素養，讓感性和理性認知相結合，讓學生從形象理解向抽象思維延伸。把“數”和“形”有機地結合在一起，這不僅是數學自身發展的需要，也是社會發展賦予教育的基本任務。

參考文獻：

[1]李 燕.數形結合，讓數學思維動起來——小學數學數形結合教學實踐論述[J].教育觀察，2019（8）：108-109.

[2]王東鳳.小學數學教學中數形結合思想的應用[J].數學學習與研究·教研版，2019（7）：61.

[3]王 倩.解析培養小學生數形結合意識的途徑[J].數學學習與研究，2017（20）：46.