基于物種敏感度分布的概率生態風險評價的Matlab實現

馮永亮

(唐山學院 基礎教學部，河北 唐山 063000)

0 引言

物種敏感度分布(Species Sensitivity Distribution，SSD)是一種用于描述不同物種對某個脅迫因素敏感度差異的統計分布模型。SSD的概念最早于1978年由美國環保局(U.S.EPA)在推導全國環境水質標準時提出，隨后于1985年確定了以SSD的5%分位數所對應的濃度(HC5)推導環境基準值，并以此代替之前的專家判斷法，沿用至今[1]。我國在2017年頒布的《淡水水生生物水質基準制定技術指南》中也推薦使用SSD模型進行淡水水生生物水質基準推導。此外，隨著SSD理論的發展，許多學者開始采用SSD與環境監測數據相結合的概率方法評價污染物的生態風險[2-5]。Chen[3]分別采用急性和慢性毒性數據，構建了9種污染物的SSDs曲線，并結合環境監測濃度構建聯合概率曲線(JPCs)評價了中國臺灣北部基隆河中污染物的生態風險，發現Zn和Cu的風險最高，有機物的風險可忽略。目前SSD模型在許多國家和地區得到了很好的應用[6-7]，已經成為污染物環境質量標準制定和生態風險評價的核心方法。

隨著SSD理論的發展和廣泛應用，一些學者或機構為SSD模型的構建和生態風險評價開發了相應的軟件。這些軟件大體上可分為兩類：一類是基于Excel表格開發的，如USEPA開發的一款用于因果評估的在線應用程序(CADDIS)中的SSD Generator，荷蘭國家公共衛生和環境研究所(RIVM)開發的ETX 2.0[8]；另一類是基于專業的統計軟件R開發的，如澳大利亞聯邦科學和工業研究組織(CSIRO)基于Burr III分布開發的軟件BurrlizO[9]，Kon等開發的網頁版工具MOSAIC_SSD[10]。這些軟件主要集中于SSD的構建和環境標準(HC5)的推導，存在著可選統計模型較少、未能與環境數據相結合等缺點。本研究結合環境監測數據，首次給出了基于SSD的概率生態風險評價的Matlab函數“PERA”，為污染物的生態風險評價提供技術支持。

1 SSD的原理和假設

不同生物生活史、生理、形態、行為和地域分布的差異構成了生態系統的生物多樣性。對于生態毒理學，這些生物多樣性意味著不同生物對特定污染物具有不同的敏感性。物種間的這種敏感性差異可以利用特定的概率分布曲線即SSD曲線來描述。

物種敏感度分布的基本假設是不同物種對特定污染物的敏感性能夠用一些統計分布模型(如Log-normal和Log-logistic分布等)來描述。生態毒理學的數據可以看成是來自于這些分布模型的樣本，并用于SSD參數的估計。SSD模型的基本形式見圖1。

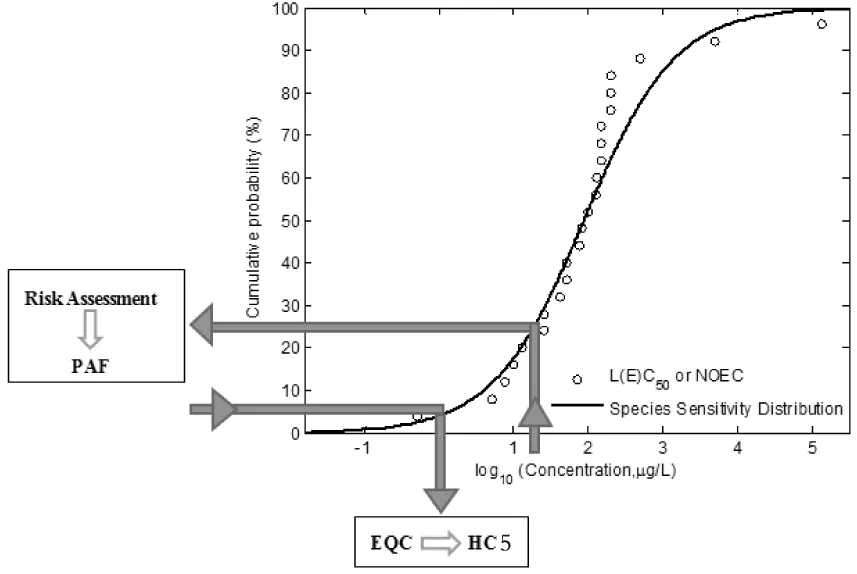
圖1 物種敏感度分布曲線示意圖

圖1中的圓圈為原始毒性數據點，可以是急性(如半數致死濃度，LC50)或慢性(如無觀測效應濃度，NOECs)效應濃度。擬合的曲線為毒性數據的累積概率曲線(即SSD)。圖中的箭頭表示SSD具有正向和反向兩個方面的應用。其中反向(箭頭Y→X)可應用于污染物的環境質量標準(EQC)的獲得，主要是通過曲線計算特定物種損害比例所對應的污染物濃度，通常取HC5作為EQC，從而保護生態系統中95%的生物不受污染物的影響；正向(箭頭X→Y)可以用于生態風險評價，主要由SSD曲線計算污染物在特定濃度下(一般為環境監測濃度)導致有害生物效應的累積概率，即受影響物種的比例(PAF)，進而定量表征污染物的生態風險。

2 基于SSD的概率生態風險評價

化學物質的生態風險主要是通過環境監測數據與毒性數據進行表征的，表征的方法包括簡單的風險商HQs法和相對復雜的概率生態風險評價法。風險商HQs法(即環境監測濃度除以毒性閾值)是簡單的單點估計法，具有簡單、透明和對數據要求低等優點，但其只適用于污染物篩選的初級階段[11-12]。為了更加精確詳細地表征生態風險，很多學者推薦采用更為復雜的概率方法，即聯合概率曲線(JPC)法。JPC方法通過比較環境監測數據和毒性數據的分布特征可以定性和定量地表征生態風險，常被用作細化各種污染物生態風險的高水平方法[13]。下面給出JPC的構建過程和其生態學意義。

設EC為污染物的環境監測濃度，SS為污染物的毒性效應濃度，隨機變量X1和X2分別來自于EC和SS的概率分布。

Pr(logEC>logSS)=Pr(X1>X2)。

(1)

式(1)為污染物的環境監測濃度大于其毒性效應濃度的概率，有兩種等價的積分形式表達式：

(2)

或

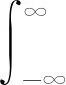
(3)

其中PDFXi，CDFXi(i=1，2)分別表示隨機變量Xi的概率密度函數和累積分布函數；式(3)中1-CDFX1(x)表示隨機變量X1超過給定數值x的概率，即傳統概率論中的生存函數，在環境毒理學中通常將其定義為超越函數EXFX1(x)=1-CDFX1(x)。此時式(3)可等價轉化為下式

(4)

由式(2)和式(4)右邊的積分表達式可知，Pr(X1>X2)即為污染物環境風險在統計學上的期望值，其在數值上等于Van Straalen[14]給出的生態風險δ和Cardwell[15]給出的期望總風險(ETR)。

基于式(4)，以毒性數據的累積概率(即dCDFX2(x))為自變量，環境監測數據的超越概率(即EXFX1(x))為因變量，構造的曲線即為聯合概率曲線(具體構建過程見圖2)。該曲線上的點表示導致不同物種損害水平的概率[2]，曲線與兩坐標軸圍成的面積即為污染物環境風險的期望值Pr(X1>X2)，也有學者稱該值為發生有害生物效應的總體風險概率(ORP)[16-17]。

類似地，JPC也可以根據式(2)進行構建，即暴露數據的累積概率(dCDFX1(x))為自變量，毒性數據的累積概率(CDFX2(x))為因變量，曲線與兩坐標軸圍成的面積為Pr(X1>X2)。

3 概率生態風險評價的Matlab程序

基于上述分析過程，構建用于污染物概率生態風險評價的Matlab函數“PERA”，其程序代碼如下所示。

function [HCq，ORP]=PERA(Tdata，q，option，ECdata)

% Tdata為污染物的毒性數據，需為向量形式。

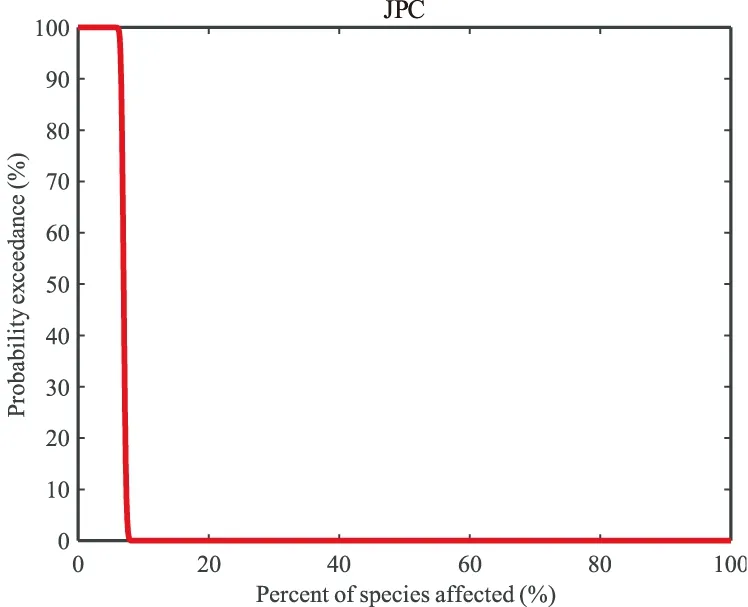
% q為SSD的q分位數HCq，0

% option=1和option=2分別表示基于Log-normal和Log-logistic分布構造SSD曲線。

% ECdata為污染物的環境監測數據，需為向量形式。

% [HCq]=PERA(Tdata，q，option)，返回SSD曲線和HCq值。

% [HCq，ORP]=PERA(Tdata，q，option，ECdata)，除返回SSD曲線和HCq值外，還返回JPC曲線和ORP值。

if nargin<3

error('輸入參數必須為3個或4個')；

end

data=sort(Tdata)；

[n，m]=size(data)；

n=max(n，m)；

p=zeros(n，1)；

for i=1：n

p(i)=i/(n+1)；

end

data1=log10(data)；

if option==1

dis='normal'；

else if option==2

dis='logistic'；

end

end

[log，logci]=mle(data1，'distribution'，dis)；

p2=icdf(dis，q，log(1)，log(2))；

HCq=10^p2；

N=10000；

mm=0.2；

mi=min(data1)；

mi=min(mi)-mm；

mx=max(data1)；

mx=max(mx)+mm；

x1=linspace(mi-0.1，mx+0.1，N)；

p11=cdf(dis，x1，log(1)，log(2))；

p=p*100；

p11=p11*100；

MS=6；

figure

plot(data1，p，'ro'，'MarkerSize'，MS，'MarkerFaceColor'，'r')

hold on

LW=1.5； % 圖像中線的寬度。

plot(x1，p11，'k-'，'LineWidth'，LW)

axis([mi-0.1，mx+0.1，0，101])；

FS=12；% 圖像中字號的大小。

xlabel('log_{10}(concentration)')

ylabel('Potentially Affected Percentage (%)')

set(gca，'FontSize'，FS，'Fontname'，'times new Roman')

set(get(gca，'XLabel')，'FontSize'，FS，'Fontname'，'times new Roman')

set(get(gca，'YLabel')，'FontSize'，FS，'Fontname'，'times new Roman')

%%以下程序用于構造聯合概率曲線JPC。

if nargin==4

data2=log10(ECdata)；

[phat，pci]=mle(data2，'distribution'，'normal')； %擬合環境數據的參數。

y=0：0.00001：1；

p22=icdf(dis，y，log(1)，log(2))； %求SSD的反累積對數濃度數值。

p33=cdf('normal'，p22，phat(1)，phat(2))； %求相對于SSD反累積對數濃度數值對應的環境監測數據的累積函數值。

p44=1-p33； %求相對于SSD反累積數值對應的環境監測數據的超越概率。

ORP=trapz(y，p44)； %計算JPC曲線與兩坐標軸所圍區域的面積。

p44=p44*100；

y=y*100；

figure

plot(y，p44，'r'，'LineWidth'，LW)

title('JPC'，'Fontname'，'times new Roman'，'FontSize'，FS)

xlabel('Percent of species affected (%)')；

ylabel('Probability exceedance (%)')；

set(gca，'FontSize'，FS，'Fontname'，'times new Roman')

set(get(gca，'XLabel')，'FontSize'，FS，'Fontname'，'times new Roman')

set(get(gca，'YLabel')，'FontSize'，FS，'Fontname'，'times new Roman')

end

4 Matlab程序的應用實例

采用Li[5]對萊州灣西部表層海水重金屬Zn的環境監測數據(2016年9月監測)和Zn對海洋生物的慢性毒性數據對本文Matlab程序進行實際運行。

給定Zn的毒性數據Tdata=[20，1000，1144.962，97，1000，2154.395，10000，142.5，313，100，10，5000，400，380，4500，1000，970，200，139，480，230，600，520，124.0718，200，178，2500，630，88.5，15000，170.2，605，55，160，64，10，500，616.4414，80，170.9976，100，270，674，2000，2768.212，960，421.7163，1000，250，160，5900，1944.402]；

Zn的環境監測數據ECdata=[39，40.6，39.1，38.6，43.6，40.4，41.2，41.9，41.1，37.8，38.4，36.8，38.4，38.7，39.1，38.5，41.2，40.7，42.4，39.5]；

在Matlab 2017b下運行：

>> [HC5，ORP]=PERA(Tdata，0.05，2，ECdata)

HC5=29.0852

ORP=0.0698

所得SSD曲線和JPC曲線分別見圖3和圖4。該結果與Li[5]的研究成果一致。

圖4 萊州灣西部表層海水中Zn的聯合概率曲線(JPC)

5 討論

專業的統計軟件R是學者們在做關于污染物生態風險評價時使用最多的一個軟件平臺[7，18-19]。R軟件強大的統計軟件包(如fitdistrplus)能夠為SSD的建立、HC5的估計等提供更多自由全面的選擇，但該軟件的熟練運用需要使用者具有一定的概率統計學功底。本文給出的Matlab函數“PERA”只需要使用者具有污染物的毒性數據就能夠方便地得到SSD曲線和其重要參數HC5，為概率統計學功底較弱的環境工作者提供了技術支持。

目前關于生態風險評價的軟件主要集中在SSD的構建和環境標準(HC5)的推導，如CSIRO開發的BurrlizO[9]，U.S.EPA開發的SSD Generator和Kon等開發的MOSAIC_SSD[10]等。這些軟件雖然可以讓使用者方便地得到SSD和HC5，但并沒有與污染物的環境監測數據相結合，無法進行污染物的概率生態風險評價。本文給出的Matlab函數“PERA”只需要使用者具有污染物的毒性數據和環境監測數據，就可以方便地得到聯合概率曲線JPC和污染物的總體風險概率ORP。雖然RIVM開發的軟件ETX 2.0也可以給出JPC和ORP，但該軟件中的SSD模型只能選Log-normal[8]，而本文所給函數中的SSD模型有Log-normal和Log-logistic兩種選擇。另外，本文所給Matlab函數的開源代碼，使用者可以對其作適當增加或修改(如增加或修改SSD模型的概率分布類型等)，較ETX2.0更具靈活性。目前關于SSD的軟件主要是基于Excel表格和專業統計軟件R開發的，尚未有基于Matlab的程序或函數，本文首次給出了基于SSD的概率生態風險評價的Matlab函數“PERA”，為污染物的生態風險評價提供進一步的技術支持。