例談數列中的奇偶項問題

◇ 李文東

數列的奇偶項是指數列中的奇數項與偶數項，高考和模擬題中經常出現按奇偶項分類求和的數列問題，這類題目對大部分學生來說難度較大，究其原因，主要是學生解題時缺乏思路.本文針對這一問題進行歸納總結，希望幫助同學們找到解題思路，以快速解決此類問題.

1 奇偶項數列的等差等比數列的證明

本題是按等比數列的定義來證明，證明過程中要注意下標的變化和適用范圍.

例2(2014年全國卷Ⅰ理17)已知數列{an}的前n項和為Sn，a1＝1，an≠0，anan＋1＝λSn－1，其中λ為常數.

(1)證明：an＋2－an＝λ；

(2)是否存在λ，使得{an}為等差數列，并說明理由.

(1)由題設anan＋1＝λSn－1，得an＋1an＋2＝λSn＋1－1，兩式相減，得an＋1(an＋2－an)＝λan＋1，由于an≠0，所以an＋2－an＝λ.

(2)由題設a1＝1，a1a2＝λS1－1，可得a2＝λ－1，由(1)知a3＝λ＋1.

假設{an}為等差數列，則a1，a2，a3成等差數列，所以a1＋a3＝2a2，解得λ＝4.

下面證明λ＝4時，{an}為等差數列.由an＋2－an＝4知，數列奇數項構成的數列{a2m－1}是首項為1、公差為4的等差數列，即a2m－1＝4m－3，令n＝2m－1，則m＝，所以an＝2n－1(n為奇數).

數列偶數項構成的數列{a2m}是首項為3、公差為4的等差數列，即a2m＝4m－1，令n＝2m，則所以an＝2n－1(n為偶數)，所以an＝2n－1(n∈N?)，an＋1－an＝2.

因此，存在λ＝4，使得{an}為等差數列.

由an＋2－an＝λ，知數列{an}的奇數項和偶數項分別構成一個公差為λ的等差數列，從而可以分別求出奇數項和偶數項的通項公式，然后再證明{an}為等差數列.

2 奇偶項數列的前n項和

類型1an＋1＋an＝f(n)，于是an＋1＋an＋2＝f(n＋1)，從而an＋2－an＝f(n＋1)－f(n).特別地，若f(n)＝an＋b(a，b為常數)，則an＋2－an＝a，即數列{an}的奇數項和偶數項分別構成一個公差為a的等差數列.

例3已知數列{an}滿足an＋1＋an＝4n－3(n∈N?).

(1)若數列{an}是等差數列，求a1的值；

(2)當a1＝2時，求數列{an}的前n項和Sn.

(1)若數列{an}是等差數列，則

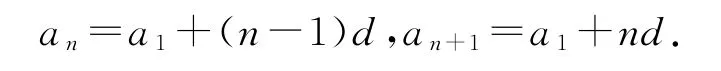
由an＋1＋an＝4n－3，得

兩式相減，得an＋2－an＝4，由a2＋a1＝1，a1＝2，得a2＝－1，所以數列{a2n－1}是首項為a1＝2、公差為4的等差數列，數列{a2n}是首項為a2＝－1、公差為4的等差數列，所以

當n為奇數時，an＝2n，an－1＝2n－7.

本例中由于數列{an}的奇數項和偶數項分別構成等差數列，其通項公式可分別求出，因此方法1對n分奇偶項討論并且每一種情況按奇數項和偶數項組合進行求和；方法2基于an＋1＋an＝4n－3的一個整體運用，將相鄰兩項組合后首先求得數列{an}的前2n項的和，進而得到n為偶數時的Sn，而當n為奇數時，利用Sn＝Sn＋1－an＋1來求.當然這里還是需要知道an＋1，這兩種方法是求解奇偶項數列前n項和的兩個基本策略.數列中的奇數項、偶數項的問題實質上是將一個數列分成兩個新的數列進行考查，易搞錯的是新數列與原數列的項數、公差、公比的判定.

例4已知數列{an}中，a1＝1，a2n＝n－an，a2n＋1＝an＋1，數列{an}的前n項和為Sn，求S100.

由題意a2n＋a2n＋1＝n＋1，于是

我們只需要求出a100即可，由于a2n＝n－an，a2n＋1＝an＋1，故a100＝50－a50，a50＝25－a25，a25＝a12＋1，a12＝6－a6，a6＝3－a3，a3＝a1＋1＝2，得a100＝31，從而

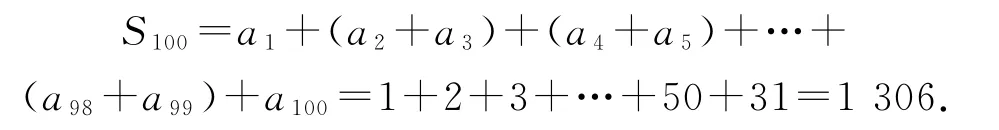
本題采用鄰項結合、整體求解，關鍵是求出a100，這根據條件一步步倒推容易得出.

①中小型第三方物流企業，根據中國物流與采購聯合會和全國物流標準化技術委員會協助制定的《物流企業分類與評估指標》，認為中小物流企業的內涵所謂中小型物流企業，是根據企業固定資產年營業額、年上繳利稅和企業員工規模劃分的一類企業形態[5]。當前一般指那些固定資產1000萬元以下、年營業額數百萬至數千萬、企業員工500人以下的為中小型物流企業。多數為單向型物流企業，它僅僅承擔和完成某一項或少數幾項物流功能[6]。

類型2an＋1·an＝f(n)，于是an＋1·an＋2＝f(n＋1)，從而.特別地，若f(n)＝a·qn(a，q為非零常數)，則＝q，即數列{an}的奇數項和偶數項分別構成一個公比為q的等比數列.

例5已知數列{an}中

(1)求證：數列{a2n}與{a2n－1}都是等比數列；

(2)求數列{an}的前n項和Sn.

類型3an＋1＋(－1)nan＝f(n)，于是當n為奇數時，an＋1－an＝f(n)，n為偶數時，an＋1＋an＝f(n)；從而當n為奇數時，n＋1為偶數，故

于是

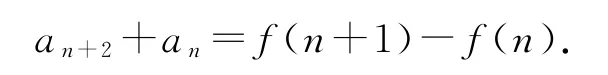
當n為偶數時，n＋1為奇數，故

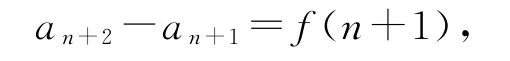
于是

特別地，若f(n)＝an＋b(a，b為常數)，則

bn＝a4n－3＋a4n－2＋a4n－1＋a4n＝f(4n－2)－f(4n－3)＋f(4n－1)＋f(4n－2)＝8an＋2b－2a，可見數列{bn}是一個首項為6a＋2b、公差為8a的等差數列.

例6(2012年全國卷Ⅰ理16)已知數列{an}滿足an＋1＋(－1)nan＝2n－1，則{an}的前60項和為______.

方法1由題意得f(n)＝2n－1，于是當n為奇數時an＋2＋an＝f(n＋1)－f(n)＝2，當n為偶數時an＋2＋an＝f(n＋1)＋f(n)＝4n.故

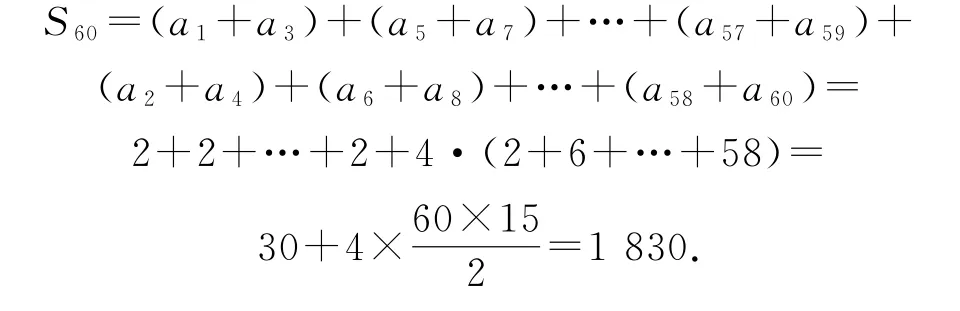
方法2bn＝a4n－3＋a4n－2＋a4n－1＋a4n是一個首項為10，公差為16的等差數列，于是

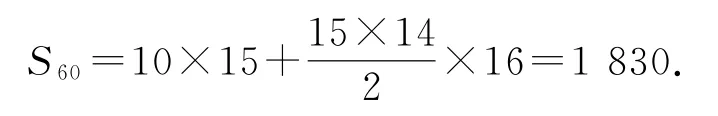
由題目分析知當n為奇數時，an＋2＋an＝an＋2＋an＋4＝2，從而an＋4＝an，若a1＝1，則a4n－3＝1，又a4n－3＋a4n－1＝2，故a4n－1＝1，于是當n為奇數時an＝1，an＋1－an＝2n－1，于是當n為偶數時an＝2n－2，即本題是一道填空題，故假設a1＝1也不失為一種有效的辦法.

3 通項含有(－1)n的數列的單調性問題

例7已知數列{an}(n∈N?)滿足a1＝1－3k，an＝4n－1－3an－1(n≥2，k∈R).

(1)求數列{an}的通項公式；

(2)若數列{an}為遞增數列，求k的取值范圍.

數列的單調性問題，本質上是an＋1－an＞0(或an＋1－an＜0)的不等式恒成立問題，數列{an}的通項公式中含(－1)n，就需對n進行奇偶性討論，確定(－1)n的值再分離變量轉化為數列最值問題.