高速鐵路有砟軌道對弓網動態性能影響分析
關金發,于素芬,孔 勇,張 毅
(1.西南交通大學電氣工程學院,成都 610097; 2.中鐵工程設計咨詢集團有限公司電化通號設計研究院,北京 100055)
目前國內350 km/h高鐵普遍采用無砟軌道,采用有砟軌道國內還沒有成熟的應用先例。為發展有砟軌道,需論證其對高速鐵路相關專業的影響,因此,有必要開展高速鐵路有砟軌道對弓網動態性能的影響,從弓網關系角度論證有砟軌道的高速適用性。
從事機車動力學研究的方法主要是利用計算機仿真模擬。文獻[1-2]利用計算機仿真,建立車輛與軌道耦合動力學模型,得到高速列車車體、懸掛、軌道各部分的振動響應,但計算模型并未考慮弓網系統。文獻[3-12]利用計算機仿真,分別建立了不同的受電弓與接觸網耦合動力學模型,得到受電弓和接觸網各部分的振動響應,但計算模型忽略車體振動。文獻[13-18]利用計算機仿真,分別建立了不同的受電弓與接觸網、車輛與軌道、軌道與線路之間大系統耦合動力學模型,研究車輛與無砟軌道對弓網動態行為的影響,但對于有砟軌道對弓網動力性能的影響尚未見有關研究。
基于此,針對中國高鐵典型弓網系統,利用離線計算方法,建立有砟軌道-車輛-弓網耦合動力學模型,分析不同運行速度高速動車組通過有砟軌道接觸網的弓網動態性能,研究有砟軌道對弓網動態性能的影響程度,為高速鐵路有砟軌道應用以及有砟軌道下弓網系統設計提供參考依據。
1 仿真建模及輸入
1.1 有砟軌道-車輛-弓網耦合動力學模型
基于動力學理論,建立了有砟軌道-車輛-弓網耦合動力學模型,如圖1所示。
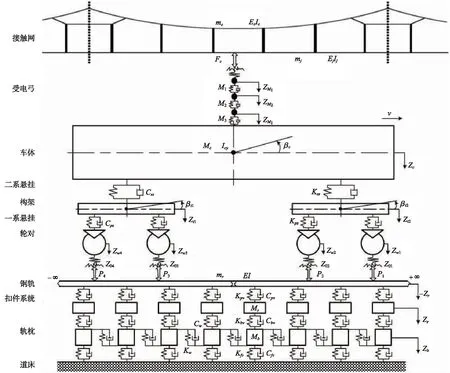
圖1 有砟軌道-車輛-弓網耦合動力學模型
有砟軌道-車輛-弓網耦合動力學模型由接觸網子系統、弓與車輛子系統、軌道子系統、弓網關系和輪軌關系五個部分構成。
接觸網子系統由承力索、接觸線、彈性吊索、吊弦和定位器組成。線索為連續質量的非線型索單元,定位器為連續質量梁單元。
弓與車輛子系統由受電弓、車體、構架和輪對等10個剛體構成,其中受電弓考慮弓頭、上框架和下框架等3個垂向自由度,車體和構架考慮浮沉、橫移、點頭、搖頭、側滾等5個自由度,輪對考慮浮沉、橫移、搖頭、側滾和旋轉等5個自由度,車輛子系統共計41個自由度。
有砟軌道子系統由鋼軌、扣件系統、軌枕、道床構成。鋼軌模擬為連續彈性離散點支承基礎上的無限長歐拉梁,具有垂向、橫向和扭轉自由度。對于有砟軌道子系統,軌枕模擬為具有垂向、橫向和轉動自由度的剛體,道床離散為具有垂向自由度的剛性質量塊,鋼軌與軌枕、軌枕與道床塊,以及道床塊與路基之間均用彈簧和阻尼元件連接。
弓網關系作為連接接觸網子系統和弓與車輛子系統的紐帶,采用非線性接觸模型進行模擬,其中弓網接觸力按照罰函數法計算。
輪軌關系作為連接車輛子系統和軌道子系統的紐帶,采用輪軌空間動態耦合模型進行模擬,其中輪軌法向力按照赫茲非線性彈性接觸理論計算,輪軌蠕滑力按照Kalker線性理論計算并進行非線性修正。
考慮受電弓質量比車體質量小得多,弓網振動對車輛振動的影響幾乎可以忽略,因此,采用了離線計算的方法,首先進行軌道-車輛動態耦合計算,得到受電弓底座的振動位移,再輸入到弓網動態耦合計算,最終得到弓網動態響應指標。
1.2 有砟軌道-車輛參數輸入
考慮高速鐵路多為橋梁結構,故線路輸入考慮為直線橋梁。橋梁段有砟軌道不平順樣本根據Q/CR 508—2016《高速鐵路有砟軌道不平順譜》[19]反演得到,如圖2所示。
選取CRH380B型動車組為研究對象,考慮250,300,350,385 km/h和420 km/h五個速度等級,車輛運行距離為2 000 m。計算結果提取前、后帶弓車輛的動力學響應。
CRH380B型動車組以不同速度在路基段有砟軌道上運行時前、后帶弓車受電弓底座處垂車體位移時域波形如圖3所示,車體垂向最大位移為15 mm。以此作為受電弓底座的垂向振動位移,輸入到弓網動態仿真模型中。
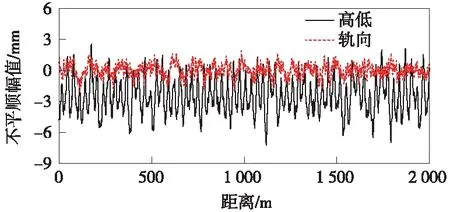
圖2 有砟軌道不平順樣本

圖3 不同速度等級有砟軌道車體垂向振動曲線
1.3 弓網參數輸入
根據TB 10621—2014《高速鐵路設計規范》[20]相關要求,以京張高鐵350 km/h速度等級接觸網為例,接觸網的仿真技術參數如表1所示。
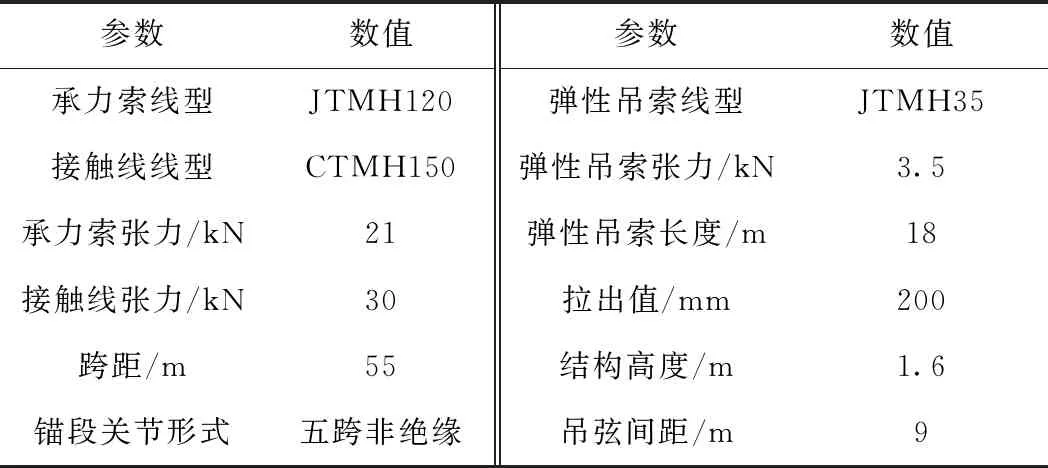
表1 接觸網技術參數
受電弓選用DSA380型,等效為三質量-剛度-阻尼模型,其參數如表2所示[21]。受電弓數量為2架,弓間距為200 m。受電弓的靜態接觸力按70 N計算,氣動抬升力按0.000 97v2計算,其中v為受電弓運行速度(單位為km/h)。

表2 受電弓模型參數
2 有砟軌道弓網動態性能
CRH380B動車組以不同運行速度通過有砟軌道,經弓網動態仿真計算,得到有砟軌道條件下弓網接觸力,如圖4所示。隨著運行速度的增加,雙弓接觸力的波動逐漸增加,后弓接觸力比前弓波動大。統計雙弓接觸力如表3所示。350 km/h及以下雙弓接觸力所有指標滿足標準要求。385 km/h和420 km/h單弓除接觸力最大值大于350 N外,其他接觸力指標滿足標準要求。385 km/h后弓通過錨段關節時接觸力最小值為0,但在錨段中部滿足標準要求。420 km/h后弓接觸力最大值和0.3Fm-σ指標不滿足標準要求。

圖4 不同速度等級有砟軌道雙弓接觸力曲線
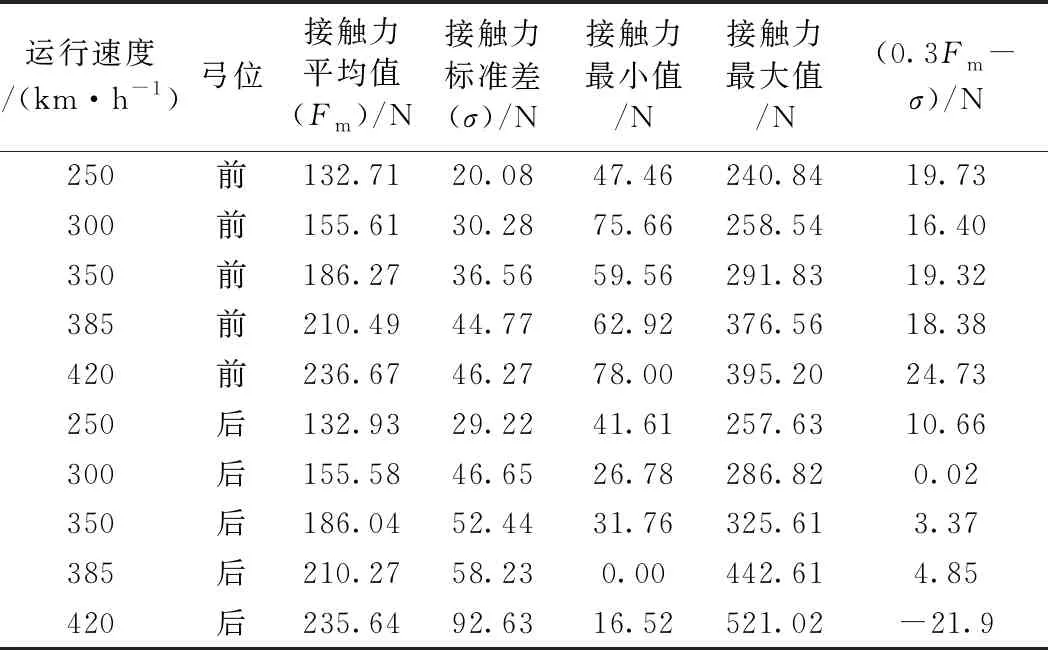
表3 不同運行速度有砟軌道雙弓接觸力統計結果
3 與理想工況下弓網動態性能對比
不考慮有砟軌道和車輛對弓網的影響,受電弓底座位移為0,經弓網動態仿真計算,得到理想工況下弓網接觸力,統計雙弓接觸力如表4所示。350 km/h及以下雙弓接觸力所有指標滿足標準要求。
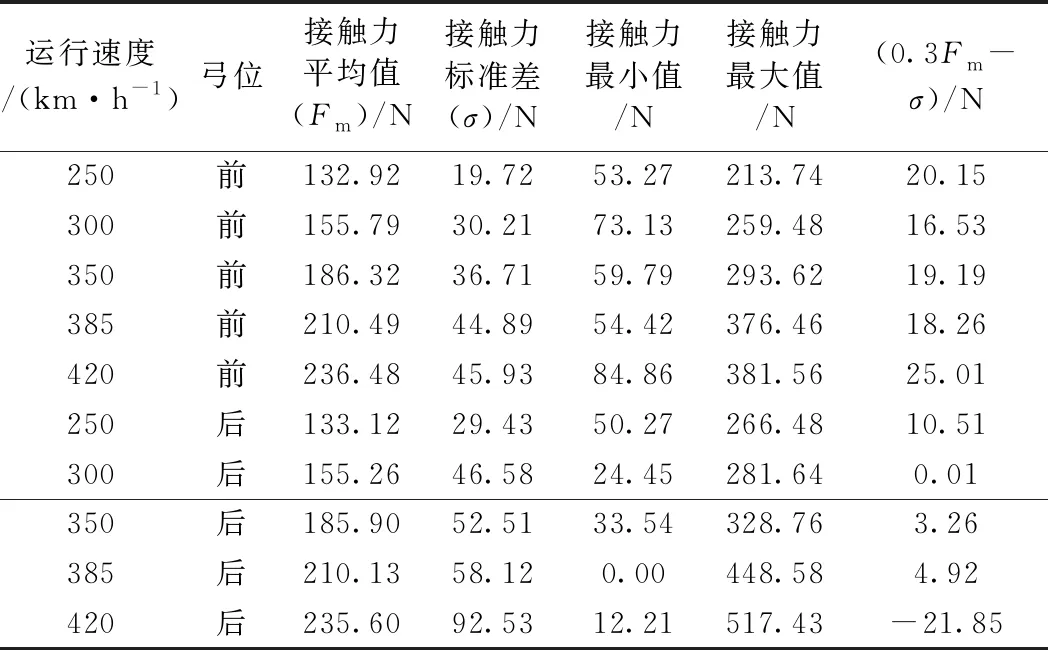
表4 不同運行速度理想工況下弓網接觸力統計結果
對比有砟軌道和理想工況的雙弓0.3Fm-σ,如圖5所示,發現兩者非常接近,說明有砟軌道-車輛對弓網動態性能的影響非常小,在計算弓網動態性能時可忽略軌道-車輛的影響。
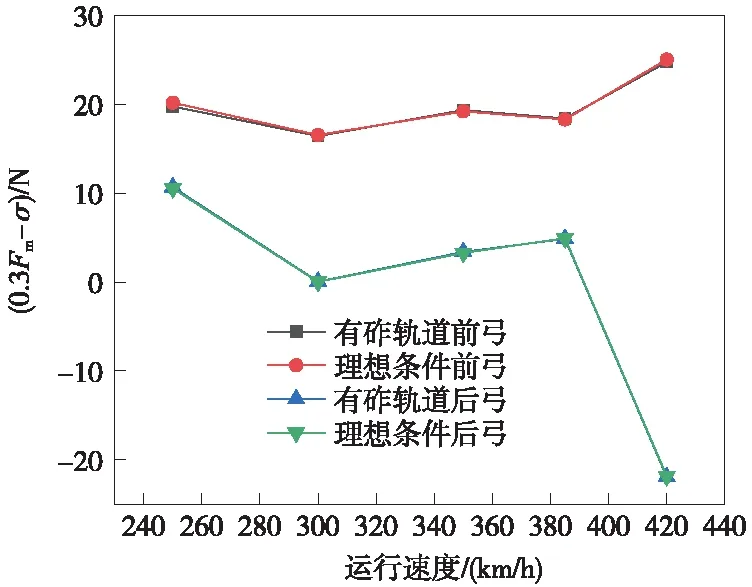
圖5 不同速度等級有砟軌道與理想工況雙弓0.3Fm-σ
4 結論
根據有砟軌道的結構特點,建立有砟軌道-車輛-弓網耦合動力學模型,計算不同運行速度下的弓網接觸力,結論如下。
(1)隨著運行速度的增加,有砟軌道-車輛-雙弓接觸力的波動逐漸增加,后弓接觸力比前弓波動大;350 km/h及以下CRH380B型動車組通過有砟軌道接觸網的雙弓接觸力所有指標滿足標準要求。
(2)有砟軌道和理想工況的雙弓接觸力指標非常接近,有砟軌道-車輛對弓網動態性能的影響非常小,在計算弓網動態性能時可忽略軌道-車輛的影響。

