具有垂直傳染和年齡結構的MSEIR傳染病模型的穩定性

粟 丹，趙 春

（天津師范大學數學科學學院，天津 300387）

傳染病的出現和傳播會給人類的生存和發展帶來嚴重威脅，因此建立恰當的數學模型來分析傳染病的傳播規律進而控制疾病的傳播是十分重要的.垂直傳染（指胎兒由母體得到疾病）作為一種特殊的疾病傳播方式在維持疾病的延續中起著重要作用，目前對具有垂直傳染和年齡結構的傳染病模型的研究較少[1-3].文獻[1]研究了具有垂直傳染和年齡結構的SEIR傳染病模型的穩定性.文獻[2]研究了一類帶有垂直傳染的年齡結構SIR流行病模型的解的存在唯一性.文獻[3]研究了帶有垂直傳染和具有年齡結構的接種流行病模型的解的存在性.

當母體感染某種傳染病后，她體內將產生相應抗體，對處于潛伏期、染病期和已恢復的母體，她們所生育的子代在一個短暫時期內具有自然免疫力，稱為被動免疫，當被動免疫消失后，子代則變成易感者.本文考慮在以往具有年齡結構的傳染病模型[4-8]的基礎上添加被動免疫，研究一類具有垂直傳染和年齡結構的MSEIR傳染病模型的穩定性.

1 模型建立

將人群分為被動免疫類、易感類、潛伏類、染病類和免疫類.M（a，t）、S（a，t）、E（a，t）、I（a，t）和R（a，t）分別表示被動免疫類、易感類、潛伏類、染病類和免疫類人群在t時刻年齡為a的人口密度.b（a）和 μ（a）分別表示與年齡相關的出生率和自然死亡率.[δ（a）]-1、[τ（a）]-1和[γ（a）]-1分別為平均被動免疫周期、平均潛伏周期和平均染病周期，不考慮因病死亡，κ1和κ2分別為E和I的垂直傳染率.設傳染病以混合比例方式傳播，令水平傳染力函數為

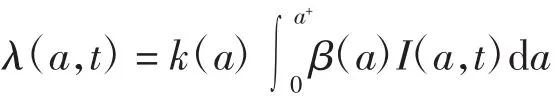
其中：a+＞ 0，k（a）為與年齡相關的接觸率，β（a）為與年齡相關的染病率.

建立MSEIR模型為

其中Q=（0，T）×（0，a+），且初邊值條件為

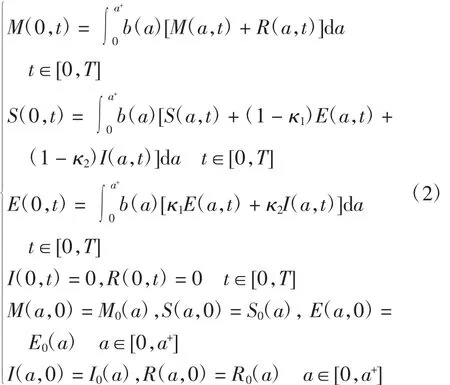
本文假設模型（1）～（2）滿足如下條件：

（A1）b（a）、δ（a）、τ（a）、γ（a）、β（a）、k（a）∈L∞[0，a+]，且b（a）、δ（a）、τ（a）、γ（a）、β（a）、k（a）均非負.

（A2）M0（a）、S0（a）、E0（a）、I0（a）、R0（a）∈L1[0，a+]，且M0（a）、S0（a）、E0（a）、I0（a）、R0（a）均非負.

（A3）μ（a）∈L∞loc[0，a+]，μ（a）≥0，且

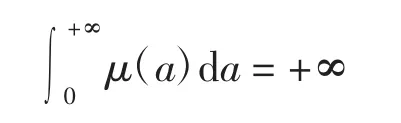
定義若（M，S，E，I，R）∈（L∞（0，T）；L1（0，a+））5在每條特征線a-t=l上都絕對連續，（a，t）∈Q，l∈R，且M、S、E、I、R滿足式（1）及

則稱（M，S，E，I，R）為模型（1）～（2）的解.

2 解的存在唯一性

令

則模型（1）可寫為

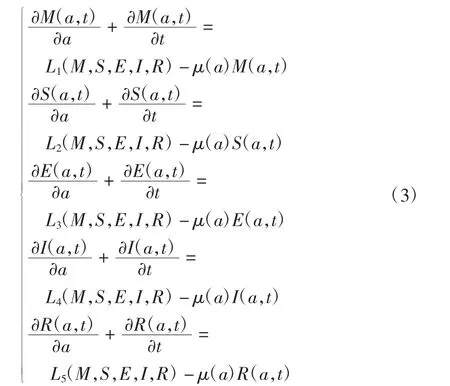
記（x1，x2，x3，x4，x5）=（M，S，E，I，R），定義解的空間為

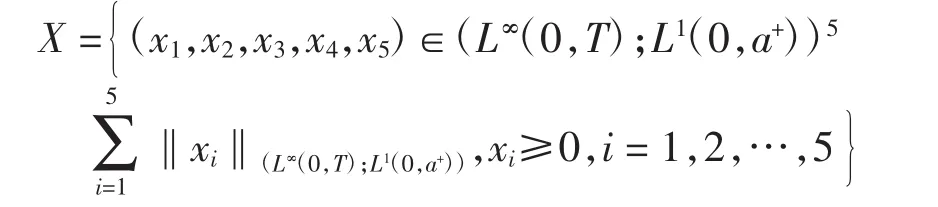
利用特征線法求解模型（3），可得

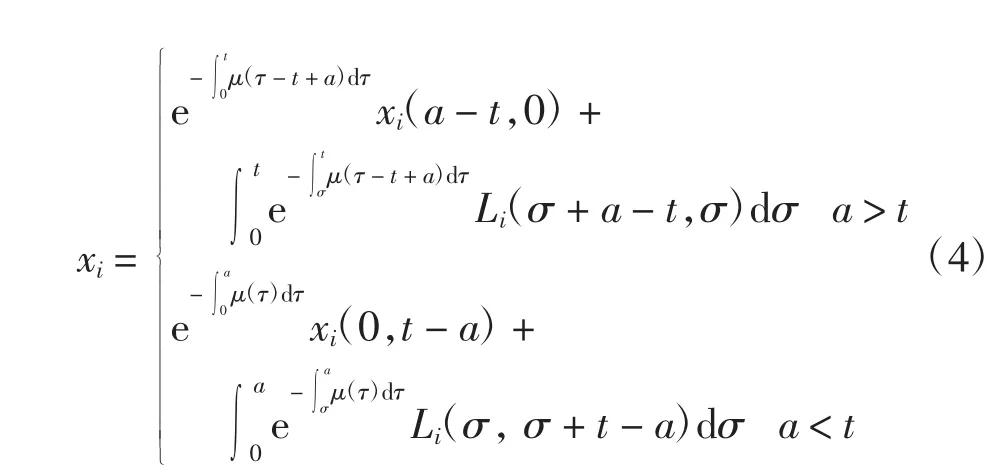
令

P（a，t）=M（a，t）+S（a，t）+E（a，t）+I（a，t）+R（a，t）則P（a，t）滿足

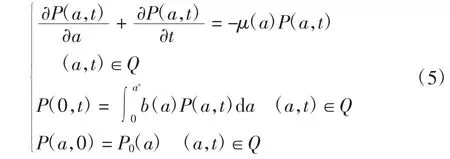
由文獻[9]可知，存在常數

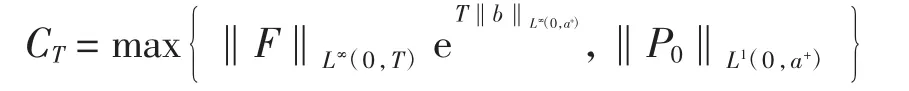
使得在（0，T）上幾乎處處滿足‖P（·，t）‖L1（0，a+）≤CT，其中

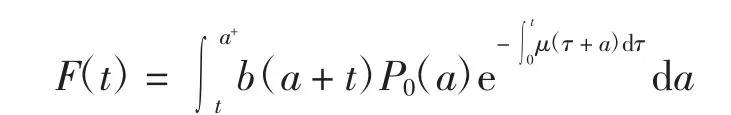
定理 1設條件（A1）~（A3）成立，則模型（1）~（2）在空間X中存在唯一解（M，S，E，I，R）.

證明定義映射Π：X→X及等價范數為

則對任意 y1、y2∈X，有

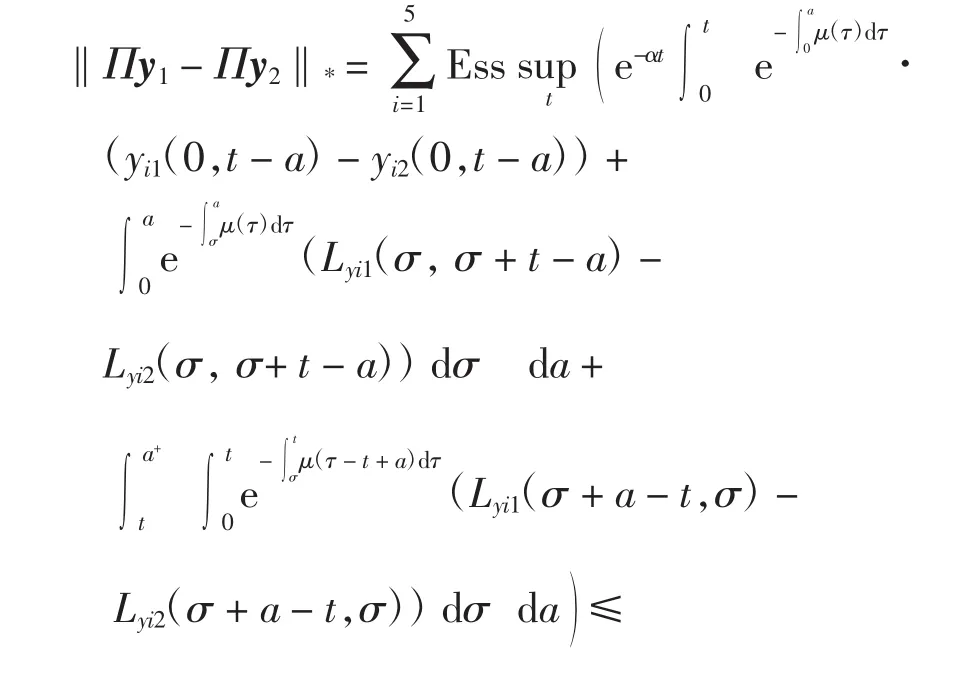
且有

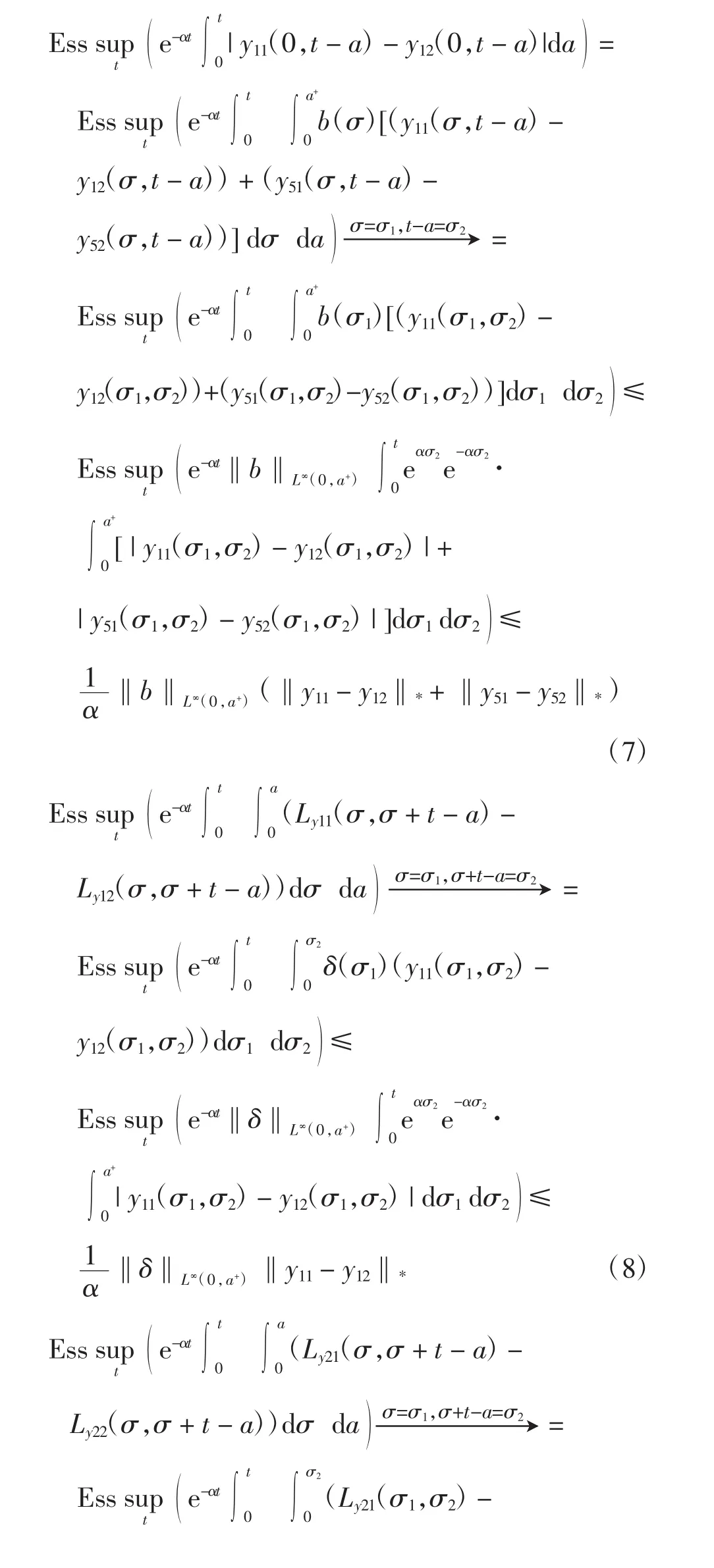
同理于式（7）可得

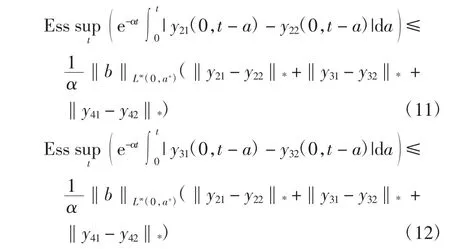
同理于式（8）~式（9）可得

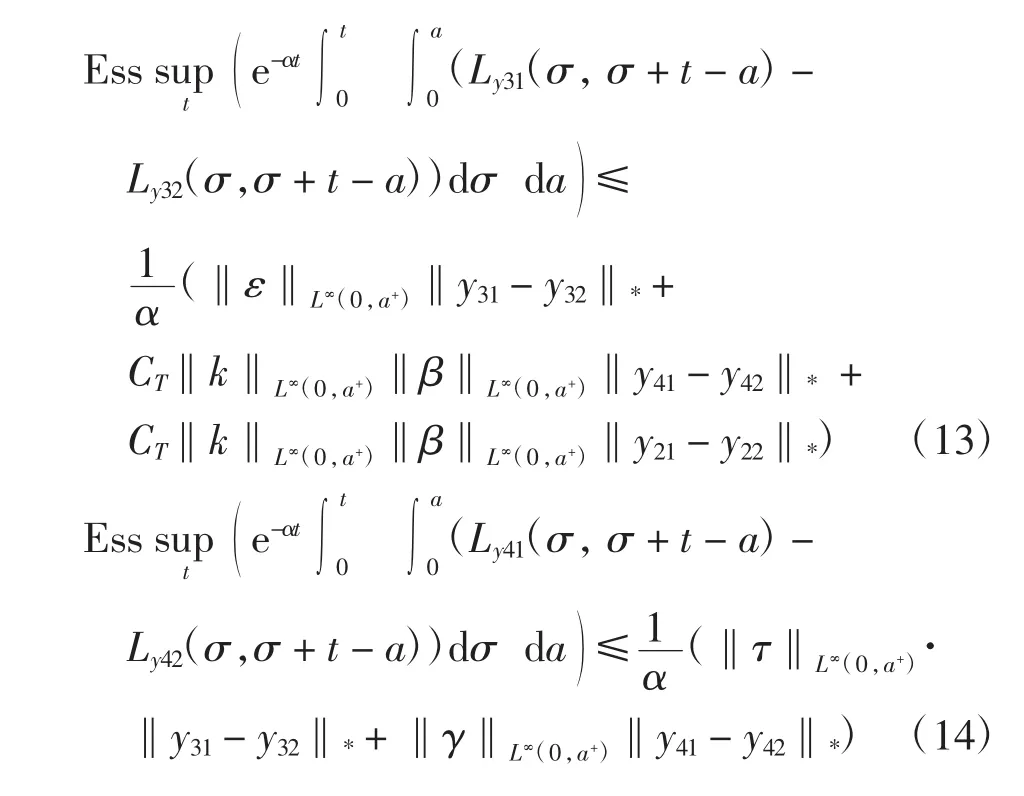
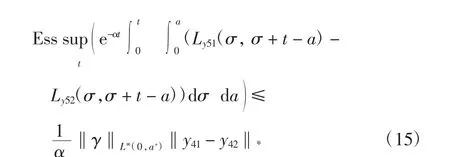
利用式（7）~式（15），結合式（6）可得

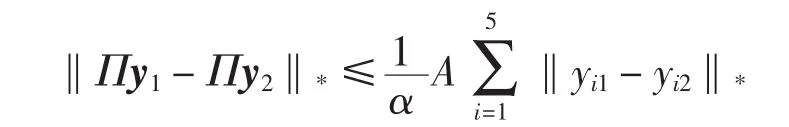
其中A是與‖δ‖L∞（0，a+）、‖τ‖L∞（0，a+）、‖γ‖L∞（0，a+）、‖β‖L∞（0，a+）、‖k‖L∞（0，a+）有關的常數.顯然當 α＞A時，Π是X上的壓縮映射，則Π存在唯一的不動點x0，即模型（1）~（2）存在唯一解 x0.證畢.

3 無病平衡點的穩定性

假設人群處于穩定狀態，即

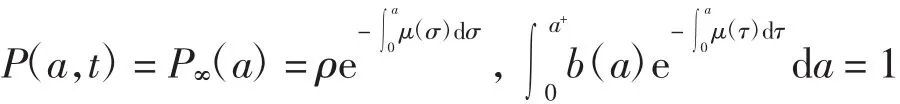
對模型（1）進行歸一化變換，令

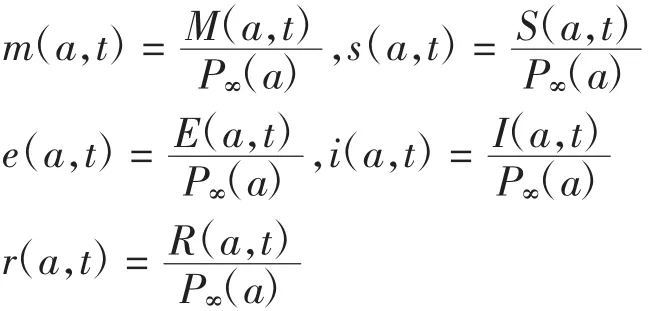
可得

模型（16）的平衡解滿足

求解模型（17）得

顯然，當β0=0時，由式（18）可得e（a）≡i（a）≡r（a）≡0，即存在無病平衡點

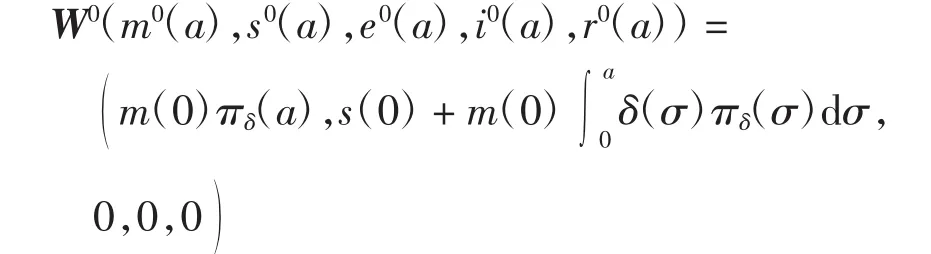
設模型（16）存在指數形式的解

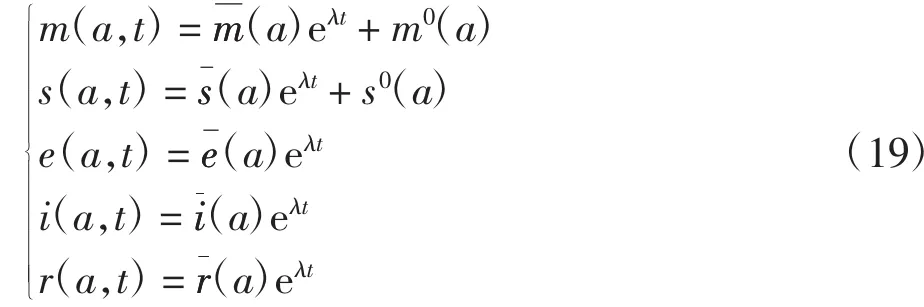
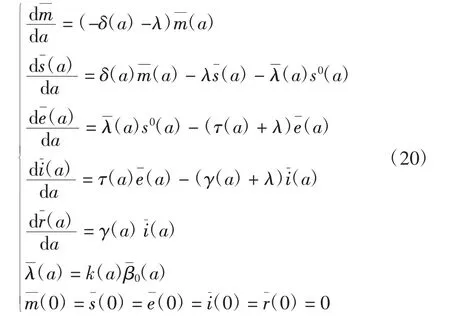
求解模型（20）得

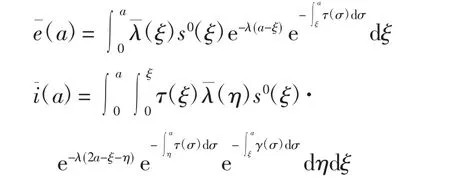
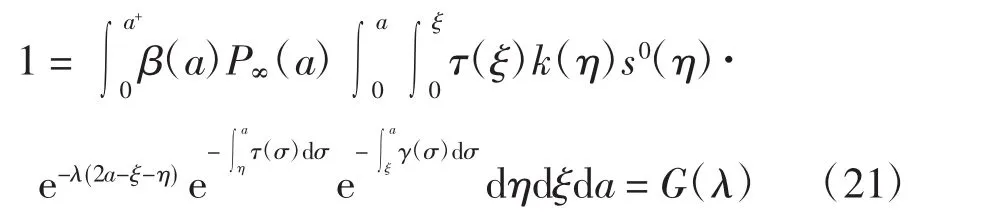
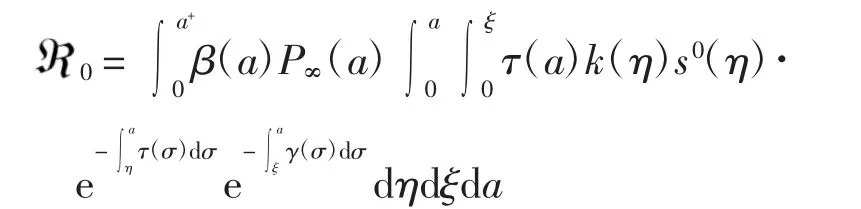
定理2若0＜1，則無病平衡點W（0m（0a），s（0a），0，0，0）是局部漸近穩定的；若0＞1，則無病平衡點是不穩定的.

證明顯然G（λ）關于λ嚴格遞減，且0.若0＜1，則特征方程（21）有唯一負實根 λ*，此時無病平衡點W0是局部穩定的.進一步，設λ=x+iy是方程（21）的任意一個復數根，x、y∈R，則由 1=G（λ*）=G（x+iy）≤G（x）可得 Re λ =x≤λ*，即 W0是局部漸近穩定的.若0＞1，則存在唯一正常數λ*滿足方程（21），即特征方程（21）有唯一的正實根，此時無病平衡點W0不穩定.證畢.