基于變剛度與力反饋的虛擬3D畫筆觸覺行為

黃磊 侯增選 李楠楠 張迪靖 蘇金輝

摘? ?要：針對汽車工業中虛擬油泥模型外觀設計問題，采用一種六自由度輸入設備并基于實時力反饋交互技術，提出一種新型的變剛度畫筆模型以及觸覺裝飾方法，實現在虛擬三維物體表面實時觸覺繪制與外觀裝飾.基于變剛度彈性理論，深入研究虛擬3D畫筆的觸覺行為.首先，采用一種彎曲彈簧振子模型來構建3D畫筆的力學模型，并分析虛擬畫筆實時變形與承受的繪制力之間的內在關系;接著，基于一種加權平均距離的碰撞算法，研究虛擬畫筆與虛擬3D物體之間的碰撞檢測問題;采用一種球擴展操作以獲得彎曲畫筆的最小包圍球，進而計算得到虛擬投影平面;根據在一個采樣點處的畫筆變形，得到虛擬投影平面上的二維筆觸;通過將二維畫筆筆觸實時地映射到三維對象表面，便可以得到三維筆觸;沿著三維繪制方向，通過控制繪制力矩并疊加不同大小、形狀的3D筆觸便可得到3D筆道.仿真對比實驗結果表明，所采用的畫筆模型及方法可以有效增強用戶虛擬繪制時的真實性.

關鍵詞：計算機觸覺;人機交互;實時力反饋;變剛度;碰撞檢測

中圖分類號：TP23 ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A? ?文章編號：1674—2974（2020）08—0049—11

Abstract：For the exterior design of virtual clay model in automotive industry， a novel variable stiffness brush model and haptic decorating method are proposed using a six DOF input device and based on real-time force feedback technology， and the haptic behavior of virtual 3D brush based on variable stiffness is studied in detail. Firstly， the relationship between brush deformation and endured force is examined by employing the bending spring-mass model to construct the 3D brush mechanical model. Then， the collision detection between virtual hairy brush and virtual 3D object is studied based on a collision algorithm of Weighted Average Distance. An effective ball expanding operation is used to compute the smallest bounding sphere of the bent brush? and then to determine the projection plane. The 2D footprint produced between the brush and the projection plane is calculated according to the deformation of the brush at a sampling point， and then， the 3D brush footprint can be obtained by projecting the 2D brush footprint onto the 3D object surface. The 3D brush stroke is formed by controlling the exerted force and superimposing 3D brush footprints along the direction of painting. Experiment results show that the adopted method can effectively enhance the reality to users.

Key words：computer haptics; human-computer interaction; real-time force feedback; variable stiffness; collision detection

無論是從企業層面還是從普通消費者的層面來講，產品外觀設計階段在工業零部件或消費產品的概念設計階段都占有非常重要的位置.產品外觀設計，包括產品形狀設計和產品外表面的裝飾，通常采用計算機輔助工業設計（Computer Aided Industrial Design，CAID）的手段或方式來完成. 傳統的CAID采用紋理映射的方法來實現從二維圖片到三維模型外表面的轉換，以此來實現3D產品外表面的裝飾[1]. 然而，從2D圖片到3D物體外表面的映射變換很容易引起原有圖形的扭曲和走樣，并且紋理映射應用的過程既繁瑣又易耗用過多的計算機內存資源. 在產品的創新設計中，設計師的靈感非常重要，而紋理映射技術需要映射二維圖形到三維物體的外表面，妨礙了設計師自由地捕捉設計靈感. 伴隨著虛擬繪畫與書法的深入發展，嘗試在3D產品模型外表面直接進行虛擬裝飾的方法開始被關注.該方法不僅能避免紋理映射存在的過度扭曲等一系列缺點，還能允許設計師完全自由發揮想象力和捕捉設計靈感. 畫筆是觸覺虛擬繪制技術的主要實施工具，藝術家通過靈活控制畫筆的位置、姿態、實時彎曲變形來完成產品創作過程. 因此，在虛擬交互式的三維繪制過程中，能否構造出一個有表現力的基于物理的虛擬3D畫筆模型是非常重要的環節.

針對虛擬畫筆建模及其繪制問題，國內外學者已做了大量研究，并取得了重要進展. Artnova系統[2]采用了一種以用戶為中心的觀看技術，通過考慮用戶的觸覺操作，將視覺和觸覺反饋集成起來，動態地確定新的視點位置. 但在系統中并未構建3D畫筆模型，這也降低了交互式繪制體驗的真實性. Gregory等[3]提供了一種直觀的基于觸覺設備的三維繪制接口，用于交互式的編輯和繪制多邊形網格. 系統通過視覺與觸覺兩種反饋能夠讓用戶自然的創建出復雜的繪制模式.然而該系統并未集成6自由度力反饋設備，并且在繪制過程中不能實現雙手交互. Fu等[4]提出了一種觸覺繪制系統，該系統為用戶提供一種簡單的方式能精確地將顏色添加到網格模型上.該繪制系統還將虛擬畫筆與一種配備了3自由度的觸覺設備集成起來. 由于真實的畫筆具有6自由度，因此該系統不能提供給用戶多種富有表現力的畫筆效果. 在虛擬畫筆建模方面，Chu等[5]提出了一種基于畫筆筆畫輪廓的建模方法，利用前后連接的貝塞爾曲線來實時模擬畫筆筆道的形成. Kim等[6-7]在原有畫筆模型的基礎上，通過添加畫筆筆毛束的幾何學模型及其相關變形算法，得到了一種新的畫筆模型，該模型可以更好地模擬真實畫筆的變形. Baxter[8]通過對原有畫筆模型加以改進，并采用能量最小化的方法來優化畫筆筆頭的幾何學表示. Larsson等[9]提

出了一種新型的畫筆模型，該畫筆幾何模型用自由運動鏈表示畫筆的中心脊骨，并利用多邊形網格表示畫筆中的筆毛簇，基于最小包圍球思想并結合能量最優化理論求解畫筆筆頭的變形.徐軍[10]于2017年在深入分析毛筆物理性能、歸納毛筆建模方法以及在總結毛筆筆法的基礎上，通過分析力對毛筆變形的影響機理，采用彈簧-振子模型構建了毛筆力反饋仿真新模型，并根據毛筆受力后的形態變化和運動變化，研究了筆道繪制算法，實現了毛筆筆道的實時繪制.

基于上述研究，本文提出了一種新型的基于物理的變剛度3D畫筆模型以及相應的三維物體表面觸覺繪制和裝飾方法，并融入實時力反饋技術和采用一臺6自由度的力反饋設備，實現了三維物體表面的交互式繪制. 在繪制時，畫筆的力覺信息可以實時傳輸給力反饋設備，因此，用戶可以通過反饋的觸覺力，實時調整繪制結果以達到預期效果.

1? ?虛擬畫筆建模

為了實現三維物體模型表面的觸覺繪制裝飾，構建一個富有表現力的虛擬3D畫筆模型是非常重要的.基于畫筆的實際特性，我們構建了一個帶有雙層結構的3D畫筆模型[11-14]，該模型融合了畫筆外在的幾何學特性和內在的動力學特性，可以模擬真實畫筆的物理特性，滿足虛擬三維物體表面自由繪制與裝飾的需求.

1.1? ?幾何學模型

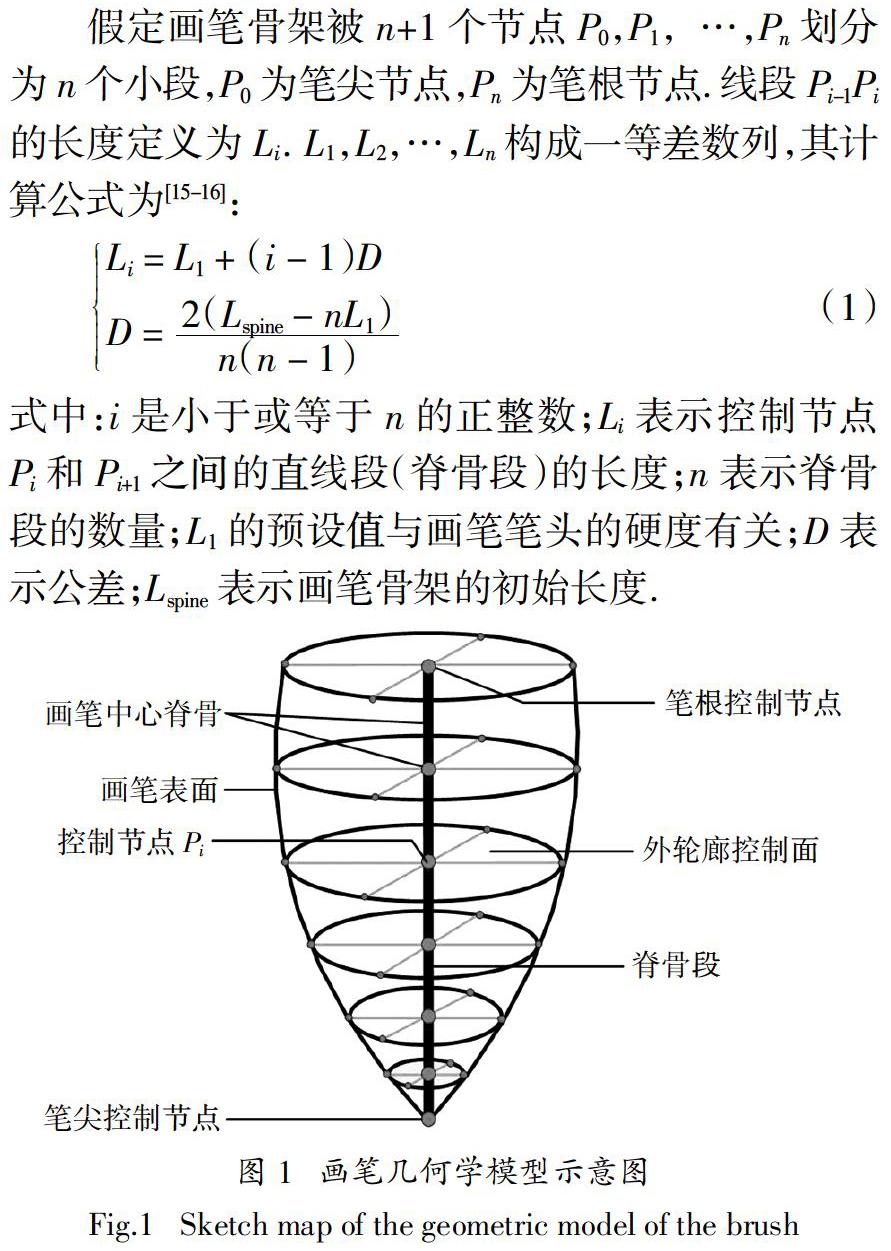
畫筆的幾何學模型與其力學模型緊密關聯. 受Chu等[5]畫筆建模方法的啟發，我們將幾何學模型（圖1）表示為一個骨架和一個經過蒙皮的表面. 脊骨骨架用于處理畫筆的常規彎曲變形. 將骨架描述為前后連接的線段序列（也稱脊骨段），并且從筆根部到筆尖部，單個脊骨段將變得越來越短.

假定畫筆骨架被n+1個節點P0，P1，…，Pn劃分為n個小段，P0為筆尖節點，Pn為筆根節點. 線段Pi-1Pi的長度定義為Li . L1，L2，…，Ln構成一等差數列，其計算公式為[15-16]：

式中：i是小于或等于n的正整數;Li表示控制節點 Pi和Pi+1之間的直線段（脊骨段）的長度;n表示脊骨段的數量;L1的預設值與畫筆筆頭的硬度有關;D表示公差;Lspine表示畫筆骨架的初始長度.

對于施加在畫筆上的相同力，畫筆筆頭越軟，則靠近筆尖處的鬃毛就越容易發生變形，此時L1的預設值就愈小，反之亦然. L1的值可以通過多次繪制實驗獲得. 公差D則由畫筆骨架的初始長度（Lspine）以及L1的值聯合決定. 當畫筆彎曲時，整個脊骨段位于同一平面內（圖2）. 筆桿的傾斜角（即筆桿與繪制紙平面形成的角度）可表示為θ（θ∈（0，π））. 而脊骨段Pi-1Pi與紙平面（虛擬投影平面）之間的夾角表示為αi（i∈[1，n]）. 如果畫筆未發生彎曲，則αi = θ. 在虛擬繪制過程中，不考慮畫筆扭曲變形，彎曲的畫筆中心骨架上所有的控制節點（P0，P1，…，Pn）都將處于同一空間平面上，該空間平面記為A0. 為了約束畫筆的變形，將一組橫截面定義為畫筆的輪廓控制面，此類橫截面垂直于空間平面A0，同時穿過控制節點Pi，且平分于鄰近的兩個脊骨段所形成夾角.畫筆表面被表示為三角網格面，該三角網格表面是由畫筆中心骨架及一系列由上至下的輪廓控制面經過蒙皮操作而形成. 當畫筆未施加任何外力時，本文中的畫筆形狀類似于一個倒錐，因此畫筆輪廓控制面在最初是一系列沿著畫筆骨架方向放置的直徑大小不同的圓.

在虛擬交互式繪制過程中，輪廓控制平面由圓變為橢圓.控制節點位置的變化引起中心骨架的變形，而每個輪廓控制面也將相應地發生位置和形狀的變化，從而引起畫筆三角網格面的變形.

1.2? ?畫筆骨架彎曲力學模型

畫筆力學模型構建的目的主要是用來仿真模擬繪制過程中畫筆受到外來施加的彎矩和壓力作用時的筆頭彎曲變形、畫筆筆頭扁曲、筆毛散開等物理現象.

引入一種變剛度彈簧質量模型[17]來仿真繪制過程中當外力矩施加于畫筆上的時候，畫筆的動態彎曲變形（圖3）.

在虛擬交互式繪制過程中，將一個遵循空間平面內彎曲變形的虛擬扁截面變剛度的彈簧置于點Pm與接觸點Pm′之間. 這里，彎曲彈簧在虛擬繪制過程中將與繪制紙平面（或虛擬投影平面）成垂直或傾斜角度，并且虛擬彈簧與其在繪制平面內的正向投影（沿著法向量方向）形成一輔助空間平面Pk，受力的畫筆將在空間平面Pk內發生彎曲變形.當畫筆筆頭剛開始接觸到繪制平面時，筆頭保持筆直狀態. 繪制過程中，隨著在畫筆筆桿端逐漸施加彎矩后，畫筆中的可變剛度虛擬彈簧將開始產生彈性甚至彈塑性彎曲. 此時，畫筆骨架中的各脊骨節點的位置將跟隨變化，同時規定各脊骨段的長度始終保持不變.

考慮實際圓畫筆的形狀特點，藝術家利用畫筆實施書畫創作時，經蘸墨后毛筆在外力矩的作用下與紙張接觸并發生彎曲變形，由于連續地運筆動作，在紙面上形成各種筆道. 基于上面的分析，我們可以得出畫筆的力學模型可以用一個變截面變剛度的彎曲彈簧或者彎曲梁來描述（以下統一稱之為彎曲梁），并且該彈簧在外力矩和紙面的共同作用下發生彈塑性彎曲變形.因此有必要深入研究該畫筆筆頭的復雜力學行為.

首先我們可以將該彎曲彈簧抽象為一虛擬矩形變剛度懸臂梁，如圖4所示，其矩形截面的寬度沿著虛擬懸臂梁的長度方向保持不變，為常數b，矩形截面的高度沿著虛擬梁的長度方向不斷變化，可用函數h（x）來表示.又規定虛擬梁的材料為理想的各向同性彈性材料.

為了降低計算的復雜度，規定虛擬梁受力彎曲變形屬于平面內彎曲，不考慮扭轉效應，那么其橫截面沿著長度x方向的高度函數及抗彎剛度函數分別為：

再假定，沿軸線方向的梁材料的屈服強度變化函數σs（x）為：

式中：σs0表示虛擬梁屈服強度的參考值系數;s（x）表示虛擬梁x截面位置對Z軸靜矩.

當畫筆骨架在受力彎曲的開始階段，變形撓度不大，其內部的虛擬彎曲梁處于彈性變形階段，對應的撓度we的微分方程為：

將式（4）實施兩次積分，則得彈性區撓度積分公式為：

式中：C1及C2表示對應的積分常數，可由具體的虛擬梁兩端的邊界條件來確定. 在虛擬繪制過程中，隨著畫筆骨架受力彎曲變形的進一步變大，伴隨虛擬梁的橫截面上的彎矩逐漸加大，當某一個橫截面上最大的彎矩達到梁的彈性彎矩的極限Me（x）時，虛擬梁將進入彈性極限彎曲狀態. Me（x）可通過下式計算得到（對于矩形截面梁）.

下面，基于具體指定的虛擬梁截面高度函數、彈性模量變化函數，進行詳細地虛擬變剛度彎曲梁（虛擬彎曲彈簧）的彈性彎曲變形分析.

1.2.2? ?彎曲骨架的彈塑性彎曲分析

本文將畫筆骨架虛擬彎曲彈簧抽象為彈性模量函數為指數變化函數，而截面高度函數為線性函數的虛擬懸臂梁.首先，虛擬懸臂梁的截面高度遵循線性變化，沿著長度方向（也為梁的軸線方向）材料的的彈性模量遵循指數方式變化，即滿足如下形式：

對于本文中的畫筆力學模型，根據實際書寫特點，可以將其力學模型抽象為左端固定右端自由的懸臂梁，忽略其自重，當在梁的自由端部施加一集中載荷P后，可把式（7）（8）代入式（5）并做積分處理，則虛擬懸臂梁（本文中的虛擬彎曲彈簧）的撓度可以表示為：

這里，Ei（z）代表指數積分函數.

1.2.3? ?力反饋分析

基于以上對畫筆模型（可變剛度梁）變形的力學分析，可以建立一個能反映出畫筆骨架彎曲變形與畫筆實時受力之間的一一對應關系基本二維查詢表，以期實現快速地力反饋計算，如表1所示.

表1中，M表示施加在筆桿處的彎矩;Pmb表示筆桿處截面的基本中心坐標，其初始值為（0，0，0）;LE表示筆頭的長度;P0b表示筆尖相對于點Pmb的基本坐標;θb表示筆尖處的截面法線相對于筆桿的相對轉角;Pib表示第i個畫筆骨架節點相對于Pmb的基本坐標;θib表示在畫筆骨架的第i個骨架節點處的截面法線相對于筆桿的相對旋轉角;mi表示施加在畫筆骨架上第i個骨架節點Pi處的彎矩.其中，M、 Pmb、LE可由力反饋設備Phantom Desktop實時提供，其余參數可由本文的算法求解獲得.

基于上述基本查詢表，可以得出許多重要的畫筆受力變形參數.其基本思想被稱之為“固定形狀法”. 固定形狀法可以被分解為兩步.

1）首先，考慮實際的畫筆繪制過程，當施加于畫筆的彎矩M、筆根中心節點Pm以及筆頭長度LE一定時，則畫筆骨架對應的彎曲變形形狀就被固定下來了（而且無論當前畫筆筆桿的實際姿態角是多少），如圖5所示.

因此，當畫筆受力產生彎曲變形后，則“基本的”虛擬畫筆筆尖點Pm0（xw，yw）的坐標（即相對于筆根中心點Pm（xm，ym））就是固定的，并且Pm0（xw，yw）可以通過使用基本查詢表并參照Pm（xm，ym）的坐標值直接得到.

2）為了得到繪制時某一采樣時刻筆尖點P0的實際坐標，可以假想將畫筆骨架受力彎曲變形的基本形狀Pm-Pm0以Pm（xm，ym）為圓心順時針旋轉α角度（如圖6所示），此時輔助過渡筆尖點Pm0剛好落在水平x軸上（即繪制平面上）. 相應地，點Pm0變換為實際繪制時的畫筆筆尖點P0（xwa，ywa），且有ywa = 0.基于圖6中的幾何學知識，可以得到：

因此，xwa = xm? - L，ywa? = 0.由角度轉換關系，筆桿的姿態角經轉換，其實剛好為α（圖6所示），它可由下式得到：

在筆尖節點處截面法線相對于豎直線（即繪制平面的法線）的絕對轉角θ（如圖5所示）可由下式計算得到：

同理，參數Pi（表示畫筆骨架上第i個骨架節點的絕對坐標值）和參數θi（表示畫筆骨架上第i個節點相對于豎直線的絕對轉角）都很容易通過計算得到（此處略去）.由繪制平面施加給畫筆筆尖部位的反力Fre（圖6）可由下式計算得到：

式中：ξm是用于反力計算的調整因子， ξm∈[0，1]，其可由多次繪制實驗獲得;Fp=（1+ξm）M/LE表示反饋力.

摩擦力可以使用戶感知三維虛擬物體表面的粗糙，并能在繪制過程中穩定控制3D畫筆.摩擦力Ff可由下式計算得到：

1.2.4? ?畫筆表面變形

在實際繪制過程中，畫筆筆頭在壓力的作用下開始與繪圖平面接觸并形成一個畫筆筆觸，筆頭從筆根到筆尖部分逐漸變的扁平. 因此，在繪制平面壓力和摩擦力的作用下，畫筆的每個輪廓控制面的形狀將逐漸從圓形變為橢圓[14]，如圖7所示.

隨著施加在畫筆上壓力的增加，橢圓的短軸 Rib將越來越短，而長軸Ria將越來越長.因此，整個橢圓將變得更加扁平.當畫筆未受到外力作用時，可以得到Ria = Rib = Ri.隨著施加在畫筆上的外力逐漸增加，橢圓的形狀不斷變化，Ria可由下式得到：

式中：mi是控制節點pi處截面的彎曲力矩;dm和em是通過實際繪制實驗得到的橢圓調整因子，以模擬在不同的繪制條件下最真實的畫筆變形;pn是壓力系數，它被定義為壓力F（繪制紙平面上的反力）與力反饋設備最大輸出力的比值.? 這里，在我們的繪制系統中，所采用的力反饋設備Phantom Desktop所能提供的最大輸出力為7.9 N，因此pn = F/7.9，其pn∈[0，1]，假定輪廓控制面的面積在變形前后保持不變，于是短軸Rib可由下式計算得到：

2? ?三維物體表面的虛擬繪制

在我們的繪制系統中，采用一種局部映射方法來實時地將二維畫筆筆觸映射到三維物體外表面.進而，通過沿繪制方向疊加3D畫筆筆觸則可以得到3D畫筆筆道. 然后，采用一種基于Kubelka-Munk的顏色光學算法對3D筆道進行實時渲染.

2.1? ?虛擬畫筆二維筆觸的形成

受Baxter及Chu等的啟發，我們假定彎曲變形后的畫筆筆頭與虛擬繪制平面相交，將筆頭穿透部分向繪制平面正向投影，則投影后的區域即為所形成的二維畫筆筆觸.該筆觸輪廓可由經關鍵控制點插值后得到的兩條對稱的B-spline曲線所組成，如圖8（b）所示. 在虛擬繪制過程中，可以通過控制筆觸輪廓上關鍵點位置以及數量從而使二維筆觸的形狀與大小發生相應調整和變化.

基于幾何學知識，線段Ni N′i為虛擬繪制平面與畫筆骨架上第i個輪廓控制圓（圓心為Pi）相交得到.筆觸輪廓控制點Md是變形的筆頭的左側輪廓線（圖8 （a））與毛筆骨架在繪制平面上的投影相交而得到，接著可以計算得到筆尖點P0的坐標值，根據P0進一步求得畫筆中心骨架上節點Pi的坐標，進而可求得筆觸輪廓控制點Ni、N′i的坐標值，相關點的具體計算過程可參考文獻[13].最后過以上關鍵輪廓控制點P0、Ni、N′i、Md，并采用B樣條曲線插值法便可得到畫筆的二維筆觸輪廓，如圖8（b）中所示.

2.2? ?虛擬畫筆與虛擬油泥3D物體間的碰撞檢測及接觸力仿真

本文采用一種OBB（Oriented Bounding Box）包圍盒算法[18-19]，以實現虛擬畫筆筆頭與三維物體外表面之間的碰撞檢測.為了確定畫筆與三維物體（如虛擬油泥模型）之間的相對位置，引入了一個帶有很小公差范圍的參數-接觸距離ddep. ddep被定義為畫筆與虛擬油泥模型表面之間的距離.如果ddep處在給定的公差范圍之內，系統將會產生一個很小的接觸力（約0.1 N），并通過力反饋設備Phantom Desktop傳遞給用戶，從而虛擬畫筆與虛擬3D模型之間的接觸可以快速地被用戶所感知.

在系統中，虛擬畫筆和虛擬三維模型的外表面被表示為三角網格，因此，ddep還可定義為筆尖P0與虛擬油泥3D模型表面上一系列若干三角網格頂點之間的加權的平均距離.這些三角網格頂點十分靠近筆尖P0點，且其個數本文中默認值通常被設定為Mn = 10. 因此，ddep可由下式定量計算得到：

式中：wi為加權系數;ni為三維物體外表面的法向量;xi為三維物體表面三角網格頂點的坐標矢量;x為筆尖節點P0的坐標矢量;di = xi - x;dmax為di的最大值.當ddep的值處在給定的容差范圍內時，用戶會感知到虛擬畫筆與虛擬油泥3D模型間的接觸或碰撞.然后，用戶可按下力反饋設備Phantom Desktop上的觸針按鈕，可將接觸力置為無效.然后，筆尖控制節點P0自動被系統約束到三維物體的表面，以便后續的觸覺繪制仿真. 筆尖P0的坐標矢量被變換為：

2.3? ?投影平面的確定

在虛擬三維繪制過程中，其中一個重要的環節就是如何建立合適的虛擬投影平面，該平面用于將二維筆觸通過特定算法實時映射到三維物體的表面，從而形成對應的三維繪制筆觸.受Larsson等[9]關于最小邊界包圍球算法的啟示，本文基于一種球擴展迭代操作建立筆頭最小包圍球.如圖9所示，頂點A為受力變形后的虛擬畫筆表任意一頂點，遍歷整個虛擬畫筆模型的表面頂點，搜索出距離頂點A最遠的畫筆模型表面頂點B，同理，再搜索出距離頂點B最遠的畫筆模型表面頂點C，以線段BC的長度作為直徑（其半徑記為r0），BC的中點D0作為球心，作球（D0，r0），并以此作為畫筆筆頭的初始邊界包圍球;頂點E為初始邊界包圍球（D0，r0）之外的畫筆上的一個頂點，我們將線段D0 E的長度表示為l1.過D0? 作D0 E的垂線并交包圍球（D0，r0）于F、G兩點.連接EF、EG、FG，則三角形FEG顯然是基底為2r0的等腰三角形，FG為包圍球（D0，r0）的直徑.然后在線段D0E上取一點D1，連接D1F，并將D0 D1的的長度記為ld1，將線段D1E的長度記為r1.然后以r1為新的半徑，以D1為圓形作新的擴展球（D1，r1）.新得到的擴展球（D1，r1）的半徑r1為：

顯然，基于幾何學知識，很容易進一步計算得到擴展球（D1，r1）的中心坐標D1以及半徑r1. 重復執行以上步驟，直到變形的畫筆筆頭模型的所有外表面頂點都被涵蓋在某一擴展包圍球中，我們把此擴展球作為畫筆筆頭的目標最小邊界包圍球（Df，rf）.

基于球擴展操作，得到了繪制筆頭模型的最小包圍球，在繪制過程中畫筆筆根處的節點Pm在虛擬三維物體表面的投影點設為Pm′（如圖10所示），以最小包圍球的球心Df為中心，搜索出距離點Df的長度小于等于rf的所有三維模型表面上的頂點，然后計算出這些頂點的各個法矢，我們取這些法矢的平均值作為待求的虛擬投影平面的法向量.同時又規定待求投影平面過點Pm′，經此操作，便確立了最終的虛擬投影平面位置.基于投影平面和畫筆的彎曲變形，可以得到繪制過程中的二維畫筆筆觸，再將得到的二維筆觸輪廓向三維模型表面反向投影，便可獲得虛擬物體表面的三維筆觸.

2.4? ?三維筆觸水墨量及筆道的形成

在交互式的3D筆道仿真過程中，含于筆頭中的水墨實時的從畫筆傳輸到與三維物體表面相接觸的部分，并將計算后的墨量及顏色填充至相接觸的區域. 通常而言，在某一采樣時刻3D筆觸中的墨量值正比于施加于畫筆筆桿的彎矩、畫筆筆頭內在對應采樣時刻所剩余水墨量.將畫筆筆頭在蘸墨后的起始包含的墨量表示為Z，在第i個采樣時刻對應的彎矩因子為Mei = Mi /（7.9 × LE），那么在最開始第一個采樣時刻點對應的3D筆觸中包含的水墨量值（Q1）可由下式計算得到：

式中：η表示不同畫筆的水墨量計算因子，該系數通過多次模擬實驗獲得，用于調整和控制虛擬繪制過程中的3D筆觸所包含的水墨量，真實再現3D物體外表面與畫筆頭間的水墨傳輸過程. 那么對應于第i個采樣時刻點的3D筆觸中所包含的水墨量可通過下式計算得到：

這里，i≥2，且i取值為正整數. 當畫筆沿著某個筆劃路徑移動時，包含在畫筆筆頭中的墨水會被傳輸到三維模型的外表面. 利用顏色光學KM理論將油墨量轉變為顏色強度值，于是在三維物體表面會形成帶顏色的三維筆觸. 具體的原理如圖11所示.

在虛擬3D繪制過程中，通過沿采樣點疊加3D畫筆筆觸可形成3D畫筆筆道（如圖12所示）.

2.5? ?畫筆筆頭分叉建模

在利用真實的畫筆去實現諸如書法、繪畫等藝術品的創作時，畫筆的筆頭分叉是一種奇特的繪制過程（物理現象），也是最難模擬的部分. 基于實際繪制經驗，觀察得出筆頭分叉與筆頭所產生的彎曲變形量、畫筆筆頭的實時含墨量有關. 當畫筆筆頭所產生的局部彎曲變形量以及實時含墨量達到某種閾值時，筆頭的筆尖處開始出現分叉現象.在分叉模型中，距離筆尖處的局部骨架將由一個骨架分化成3個子骨架，每個子骨架又被脊骨節點分成若干個小脊骨段，每個子骨架的力學模型類似于上文中講述的基本畫筆骨架建模原理，如圖13所示. 為了減少計算量，我們規定需要實現分叉的筆尖處局部骨架的長度約占整個畫筆骨架長度的1/3. 這里需要指出的是，畫筆筆頭的彎曲變形又和筆桿處所受到的彎矩M成正相關.畫筆筆頭開始出現分叉時的閾值可用SP表示，SP可由下式求得：

Mξ是分叉因子，由多次繪制實驗獲得.

3? ?仿真實驗驗證

采用所提出的觸覺畫筆模型及虛擬三維繪制方法，成功開發出基于實時力反饋技術的虛擬三維繪制系統.該系統開發使用的主要編程語言為C++，使用的集成開發環境為vs2008，界面庫采用QT，三維圖形渲染庫采用美國的商用圖形開發包openinventor，觸覺反饋庫采用Sensible公司的openhaptic開發包，數學運算庫采用科學計算庫gsl. 該三維繪制系統穩定運行于HP Xw8600工作站上，并通過串行接口集成一臺6自由度的Phantom Desktop力反饋設備（圖14）.力反饋設備可以實時提供畫筆筆桿的受力和位置等相關信息，以用于計算畫筆的實時彎曲變形和水墨傳輸過程.交互式觸覺三維繪制系統界面如圖15所示.

第一個仿真實驗內容是關于畫筆受力變形問題，所采用的畫筆參數如表2所示. 當對畫筆施加不同的壓力（Fre）時，所得到的相應畫筆變形如圖16所示.可見畫筆受力越大，彎曲變形越明顯，同時得到的筆道也越寬.

作為一個簡單的例子，中國漢字“七上八下”被繪制在一個碗模型的內表面（圖17）.

圖18顯示了使用交互式觸覺繪制系統在3D物體表面實施繪制的一個具體的實例（兩只小鴨子被繪制在一個碗模型上）.

在使用我們的畫筆模型進行的另一組仿真實驗中，畫筆參數如表2所示. 中國漢字“漫步人生”被繪制在一個盤子模型的內表面（圖19（a））. 相比于采用“Moxi” 二維繪制系統所得到的繪制結果（圖19（b）），使用我們的系統可繪制出帶有水墨擴散效果的三維筆道和字跡. 在圖20中展示了仿真實驗中得到畫筆分叉效果.

4? ?結? ?論

基于實時力反饋交互技術，提出了一種新型的變剛度虛擬畫筆模型及三維物體表面實時觸覺裝飾方法. 針對虛擬三維表面繪制問題，深入研究了帶有變剛度彈塑性的虛擬3D畫筆實時觸覺行為. 通過引入彎曲彈簧振子模型以構建3D畫筆力學模型，分析了畫筆受力、姿態、含墨量與畫筆變形之間的動態關系. 類似于但又不同于數據驅動建模技術，我們建立了一種二維查詢表，可以實現受力與相應筆頭變形的快速求解.該畫筆模型可以模擬實際畫筆的許多重要特征，如：更軟的畫筆筆尖、畫筆分叉等. 實際上這些行為都是比較復雜的非線性物理現象，我們僅做了部分的有益探索.此外，為研究虛擬畫筆與虛擬3D物體之間的碰撞檢測問題，我們引入了一種基于“加權的平均距離”的碰撞檢測算法. 再采用一種有效的包圍球擴展操作獲得畫筆的最小包圍球，并計算得到虛擬投影平面.通過將虛擬投影平面上形成的2D筆觸實時的映射到3D物體外表面就可以到畫筆的3D筆觸. 使用課題組開發的三維表面繪制系統，并運用Phantom Desktop力反饋設備，較好的實現了三維產品外表面的觸覺裝飾，極大地增強了繪制過程的真實感，同時又能支持外觀設計師創新靈感的發揮.

參考文獻

[1]? ? ZHANG E，MISCHAIKOW K，TURK G. Feature-based surface parameterization and texture mapping [J]. ACM Transactions on Graphics，2005，24（1）：1—27.

[2]? ? FOSKEY M，OTADUY M A，LIN M C. ArtNova：touch-enabled 3D model design[C]// Proceedings IEEE Virtual Reality 2002. Washington D C：IEEE Computer Society，2002：119—126.

[3]? ? GREGORY A D，EHMANN S A，LIN M C. Intouch：interactive multiresolution modeling and 3D painting with a haptic interface[C]// Proceedings IEEE Virtual Reality 2000. Washington D C：IEEE Computer Society，2000：45—52.

[4]? ? FU Y X，CHEN Y H. Haptic 3D mesh painting based on dynamic subdivision [J]. Computer-Aided Design and Applications，2008，5（1/4）：131—141.

[5]? ? CHU N S H，TAI C L. An efficient brush model for physically-based 3D painting[C]// 10th Pacific Conference on Computer Graphics and Applications. Washington D C：IEEE Computer Society，2002：413—421.

[6]? ? KIM L，SUKHAMTME G S，DESBRUN M. A haptic-rendering technique based on hybrid surface representation [J]. IEEE Computer Graphics and Applications，2004，24（2）：66—75.

[7]? ? KIM L，SUKHAMTME G S，DESBRUN M. Haptic editing of decoration and material properties[C]// 11th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems. Washington D C：IEEE Computer Society，2003：213—220.

[8]? ? BAXTER W V. Physically-based modeling techniques for interactive digital painting [D]. Chapel Hill，USA：University of North Carolina，2004：132—135.

[9]? ? LARSSON T，KALLBERG L. Fast and robust approximation of smallest enclosing balls in arbitrary dimensions[C]// Symposium on Geometry Processing. Delft，Netherlands：Eurographics Association，2013：93—101.

[10]? 徐軍. 基于力反饋技術的虛擬三維繪制關鍵技術研究[D]. 大連：大連理工大學機械工程學院，2017：30—36.

XU J. Research on key technologies of virtual 3D rendering based on force feedback technology [D]. Dalian：College of Mechanical Engineering，Dalian University of Technology，2017：30—36. （In Chinese）

[11]? PAN H B. Computer simulation and implementation in Chinese calligraphy dry brush [J]. Applied Mechanics & Materials，2014，543：1689—1693.

[12]? YAN F X，HOU Z X，ZHANG D H，et al. Virtual clay modeling system with 6-DOF haptic feedback [J]. Materials Science Forum，2009，628：155—160.

[13]? HUANG L，HOU Z X， GUO C，et al. Haptic decorating on the surface of virtual clay model [J]. Mathematical Problems in Engineering，2018，2018：1—12.

[14]? GUO C，HOU Z X，YANG G Q，et al. The simulation of the brush stroke based on force feedback technology [J]. Mathematical Problems in Engineering，2015，2015：1—10.

[15]? GUO C，HOU Z X，SHI Y Z，et al. A virtual 3D interactive painting method for Chinese calligraphy and painting based on real-time force feedback technology [J]. Frontiers of Information Technology & Electronic Engineering，2017，18（11）：1843—1853.

[16]? HUO B Y，YI W J. The theoretical analysis of dynamic response on cantilever beam of variable stiffness [J]. Engineering Sciences，2014，54（2）：93—96.

[17]? XIAO H，BRUHNS O T，MEYERS A. Elastoplasticity beyond small deformations [J]. Acta Mechanica，2006，182（1/2）：31—111.

[18]? PENG F Y，SU Y C，ZOU X M，et al. Global interference and collision detection based on hierarchical OBBTree in the 5-axis machining of impeller [J]. China Mechanical Engineering，2007，18（3）：304—307.

[19]? 胡志剛，秦啟飛. 基于凸包的最小體積有向包圍盒生成算法[J]. 湖南大學學報（自然科學版），2019，46（2）：105—111.

HU Z G，QIN Q F. Algorithm for finding minimum volume oriented bounding boxes based on convex hull [J]. Journal of Hunan University （Natural Sciences），2019，46（2）：105—111. （In Chinese）