無模型自適應去噪控制及其應用

董娜 朱碩

摘? ?要：為了使無模型自適應控制（Model-Free Adaptive Control，MFAC）更好地解決伴有噪聲干擾系統(tǒng)的控制問題，在無模型自適應控制方法的基礎上，針對伴隨噪聲干擾的系統(tǒng)進行分析研究，引入帶有濾波作用的跟蹤微分器，在反饋過程進行濾波操作，提出一種基于改進跟蹤微分器（Improved Tracking Differentiator，ITD）的無模型自適應去噪控制方法，同時給出了該算法的收斂性證明. 并通過仿真證明了本文改進的控制方法可以快速跟蹤給定信號并且具有良好的抵抗噪聲干擾特性. 最后，將其應用在循環(huán)流化床鍋爐汽包水位的控制中.

關鍵詞：控制算法;工業(yè)鍋爐的控制;無模型自適應控制;跟蹤微分器;去噪;CFB鍋爐

中圖分類號：TP273 ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A? ?文章編號：1674—2974（2020）08—0074—08

Abstract：In order to make the model-free adaptive control（MFAC） better solve the control problem with noisy system， this paper examines the noise system and applies improved tracking differentiator in MFAC. Filtering is performed in the feedback process， and a MFAC method based on improved tracking differentiator（ITD） is proposed. The convergence of the algorithm is also proved. The simulation experiment proves that the improved control method can quickly track a given signal and has good resistance to noise interference. Finally， it is applied to the control of the drum water level of circulating fluidized bed （CFB） boiler.

Key words：control algorithm;control of industrial boilers;model-free adaptive control;tracking differentiator; de-noise;circulating fluidized bed（CFB） boiler

在工業(yè)生產過程中，尤其是復雜工業(yè)過程，數(shù)據量越來越大. 因此，很難建立精確的數(shù)學模型，由此導致基于模型的控制方法難以達到期望的控制結果. 無模型控制是解決此類問題的一種有效的選擇. 典型的無模型控制方法當屬PID（Proportional Integral Differential）[1]以及PID與其他算法相結合的方法[2]. 同時也有一些其他的無模型控制方法，如文獻[3]基于同步擾動隨機算法進行了聚表二元驅優(yōu)化;文獻[4]關于迭代學習控制的研究;以及虛擬參考反饋整定[5]等，經過眾多科研人員的鉆研與推廣，這些方法取得了不同程度的發(fā)展，并且應用到了不同場景中.

侯忠生[6]于1994年提出了無模型自適應控制，相比前面提到的無模型方法，MFAC形式更加簡單，參數(shù)調節(jié)更容易，并且有嚴格的理論證明. 經過多年的發(fā)展，無模型自適應控制理論趨于完善，眾多學者基于MFAC方法也提出了一些有效的改進算法[7-8]. 而且，MFAC算法已經在實際工業(yè)過程得到了應用[9].

對于受環(huán)境干擾的復雜工業(yè)過程，MFAC的研究十分重要，然而MFAC在去噪領域的相關研究還比較少. 目前在去噪領域，小波去噪是一種典型的去噪方法，基于小波變換發(fā)展出了不同的去噪方法[10-12]，其中一些方法已經被應用到實際中. 本文在MFAC理論的基礎上，通過對不同的去噪方法進行分析研究，為了使MFAC方法更簡單、易操作地解決噪聲干擾問題，將帶濾波作用的改進跟蹤微分器[13]應用到MFAC方法中，并且通過對一些典型對象的數(shù)值仿真驗證所提方法的有效性，最后將本文方法應用到循環(huán)流化床鍋爐汽包水位控制中.

1? ?無模型自適應控制簡介

1.1? ?動態(tài)線性化模型

針對如下一般離散非線性系統(tǒng)：

1.3? ?偽偏導數(shù)估計

偽偏導數(shù)的估計算法運用如下估計準則函數(shù)：

2? ?無模型自適應去噪控制

針對伴隨噪聲干擾的系統(tǒng)，引入跟蹤微分器，相比小波去噪相關方法，跟蹤微分器形式簡單，易于調節(jié).

2.1? ?跟蹤微分器簡介

跟蹤微分器（Tracking Differentiator，TD）離散形式由文獻[15]給出，形式如下：

式中：x1為跟蹤系統(tǒng)的輸出y;x2為跟蹤系統(tǒng)輸出的微分（導數(shù)）信號;其他參數(shù)說明見文獻[15].

此方法涉及的計算過程復雜且存在相位延遲現(xiàn)象，在下文的仿真實驗中將與改進的跟蹤微分器跟蹤效果作出對比來說明這一問題. 雖然文獻[16]中提出了一種方法可以克服這個缺點，但是增加了額外參數(shù)且不易調節(jié).

為了解決這一問題，文獻[13]提出一種改進的非線性跟蹤微分器設計，不僅解決了相位延遲的問題，還解決了跟蹤緩慢的問題，達到快速跟蹤的效果. 其形式如下：

式中：x1為跟蹤輸出信號y;x2為跟蹤輸出信號y的微分信號;一般取a1>1，a2>1，p/q≥3，β≥1. a1、a2、p/q、β確定后可不再改變;R為可調參數(shù)，決定跟蹤的快慢，增大R，將加快跟蹤速度，噪聲放大也越大.

2.2? ?基于改進跟蹤微分器的無模型自適應去噪控制

將上述改進的跟蹤微分器應用到無模型自適應控制中，控制框圖（仿真系統(tǒng)圖）如圖1所示.

2.3? ?穩(wěn)定性分析

3? ?仿真和實驗

本節(jié)第一小節(jié)通過對幾個典型被控對象的仿真來驗證所提出方法的有效性. 第二小節(jié)，將本文方法應用到CFB鍋爐汽包水位的控制中.

3.1? ?數(shù)值仿真

本節(jié)分為3組仿真，在每組仿真中，本文方法都與使用原始跟蹤微分器去噪效果進行比較. 以此來驗證本文提出方法的可行性及有效性. 仿真系統(tǒng)見圖1.

第一組仿真被控系統(tǒng)為：

其中v是加入的30 dBW能量的白噪聲. 給定信號為前500個時刻y* = 1，后500個時刻y* = 0.5. 在第二組實驗中，被控對象為式（21），給定信號為前500個時刻y* = 0.5，后500個時刻為：

第三組為系統(tǒng)伴隨擾動情況下的仿真，被控對象為：

給定信號y* = 0.5.

在第一組仿真中，MFAC算法的相關參數(shù)ρ =1，η = 1，μ = 0.9，λ = 40. 改進跟蹤微分器參數(shù)為a1 = 2，a2 = 2，β = 3，p/q = 4，R=19. 仿真結果如圖2所示.

圖2 （a）為原始MFAC方法輸出信號. 圖2 （b）為MFAC-ITD方法輸出，即本文方法;圖2（c）為MFAC-TD[17]方法輸出，即反饋回路使用原始跟蹤微分器. （圖3、圖4同）.

由圖2和表1的誤差相關指標可以看出，由于原始跟蹤微分器存在相位延遲的問題，不能及時將輸出反饋，導致出現(xiàn)了嚴重的超調現(xiàn)象，大大降低了MFAC算法快速響應的良好特性. 而改進的跟蹤微分器不存在相位延遲現(xiàn)象，能快速地將輸出信號反饋，在去除噪聲的同時保持了原始MFAC算法的快速響應特性，MFAC-ITD方法控制器輸出更容易達到相對穩(wěn)定的狀態(tài). MFAC-TD方法的MAE和MSE分別為MFAC-ITD方法的4倍和6倍，進一步說明MFAC-ITD方法的快速跟蹤效果.

結合圖3和表2的相關誤差指標更能直觀地看出，對于變信號系統(tǒng)，MFAC-TD方法跟蹤效果同樣不如MFAC-ITD方法，MFAC-TD方法的MAE和MSE分別為MFAC-ITD方法的2倍多和7倍左右. 這種差別在第500 s時刻給定信號變復雜后表現(xiàn)得更加明顯.

第三組實驗仿真輸出結果比較如圖4所示，MFAC算法相關參數(shù)ρ=1，η=1，μ=0.9，λ=20. 改進跟蹤微分器參數(shù)為a1=2，a2=2，β=3，p/q=4，R=15.

結合圖4和表3的相關誤差指標可以看出，MFAC-TD方法的MAE和MSE均比MFAC-ITD方法高，而且在初始時刻和第500 s時刻，MFAC-TD方法均出現(xiàn)超調現(xiàn)象，均不能保持MFAC方法良好的快速響應特性，而MFAC-ITD方法在保持MFAC方法良好特性的同時有效地去除了噪聲干擾.

根據上述在不同仿真環(huán)境中得到的結果，可以看出，由于MFAC-ITD方法消除了MFAC-TD方法自身存在的相位延遲現(xiàn)象，既保持了MFAC方法快速響應的良好特性，又保持了跟蹤微分器去除噪聲的良好特性，對帶有噪聲干擾的系統(tǒng)達到了較為理想的控制效果，更為重要的是MFAC-ITD方法參數(shù)調節(jié)更加簡單，更具有操作性.

3.2? ?循環(huán)流化床鍋爐汽包水位控制

循環(huán)流化床（Circulating Fluidized Bed，CFB）鍋爐汽水系統(tǒng)控制的目標是控制鍋爐給水流量跟蹤蒸氣負荷要求，控制蒸氣溫度在一定范圍內，同時確保鍋爐及汽機的安全、經濟運行. 根據汽水系統(tǒng)的特點，可以在兩個方面進行控制，即汽包水位控制和主蒸氣溫度控制.

在CFB鍋爐的汽水系統(tǒng)（圖5虛線框內）中，水從給水裝置流出，經過省煤器適度加熱后去汽包，除此之外，給水裝置同樣向減溫器供水，目的在于使主蒸氣的溫度變化不至于過大. 主蒸氣經過蒸氣-水分離裝置和過熱器，最后通過減溫器成為成品蒸氣[18-19]. 圖5中虛線框中的汽水系統(tǒng)簡化為圖6的流程圖.

在CFB鍋爐中，汽包水位代表了鍋爐負荷與給水之間的平衡關系，因此，為了保證鍋爐穩(wěn)定高效，保持水位在合理的工作區(qū)非常關鍵.

圖6中虛線框內是汽水系統(tǒng)中汽包水位部分. 汽包水位的控制目的：1）保持汽包水位在合理工作區(qū)，如果過高，超過正常水位，會導致汽水分離過程出現(xiàn)問題，另外，如果蒸氣中攜帶水太多，會使過熱器壁上、渦輪葉片上造成過多的污垢，甚至葉片會因水的沖擊而破壞;如果水位過低，會導致水循環(huán)過程不正常，從而破壞整個系統(tǒng)的正常運行. 2）維持給水量一直在合理的工作區(qū)間內，進而保證省煤器正常工作和供水管無損壞.

由于爐體內影響汽水變化的對流管束的物理特性變化，所以，水位系統(tǒng)是一個慢時變系統(tǒng). 根據鍋爐汽包容量大小，閥位變化需要一定的時間才能反映到水位變化，可見系統(tǒng)具有延時，而且系統(tǒng)存在著較大的干擾，因此，汽包水位系統(tǒng)是一個具有大的擾動和非線性特性的系統(tǒng)[19].

綜上分析可知，汽包水位系統(tǒng)不存在一個精確的數(shù)學模型，而且伴隨擾動，因此，應用無模型控制方法是一很好的選擇.

從上面可以看出，作為兩個主要因素的給水量和蒸氣量對汽包水位的變化影響最大，考慮供水量對汽包水位的影響，該對象僅存在一個如下動態(tài)的數(shù)學模型[20]：

式中： T為給水擾動下的純滯后時間;Td為水位反應時間;G（s）是該控制系統(tǒng)的傳遞函數(shù);s是傳遞函數(shù)中的復變量.

通常情況下，T取值30 ～ 100 s，Td取值30 ～ 150 s，在本次實驗中，參數(shù)取T = 50 s，Td = 30 s，該模型僅用來提供輸入輸出數(shù)據. 給定信號y* = 5. MFAC-ITD算法的相關參數(shù)為η = 0.1，μ = 0.1，ρ = 1，λ = 78. 改進跟蹤微分器參數(shù)為a1 = 2，a2 = 2，β = 3，p/q = 4，R = 14.5.

汽包水位簡易控制框圖如圖7所示.

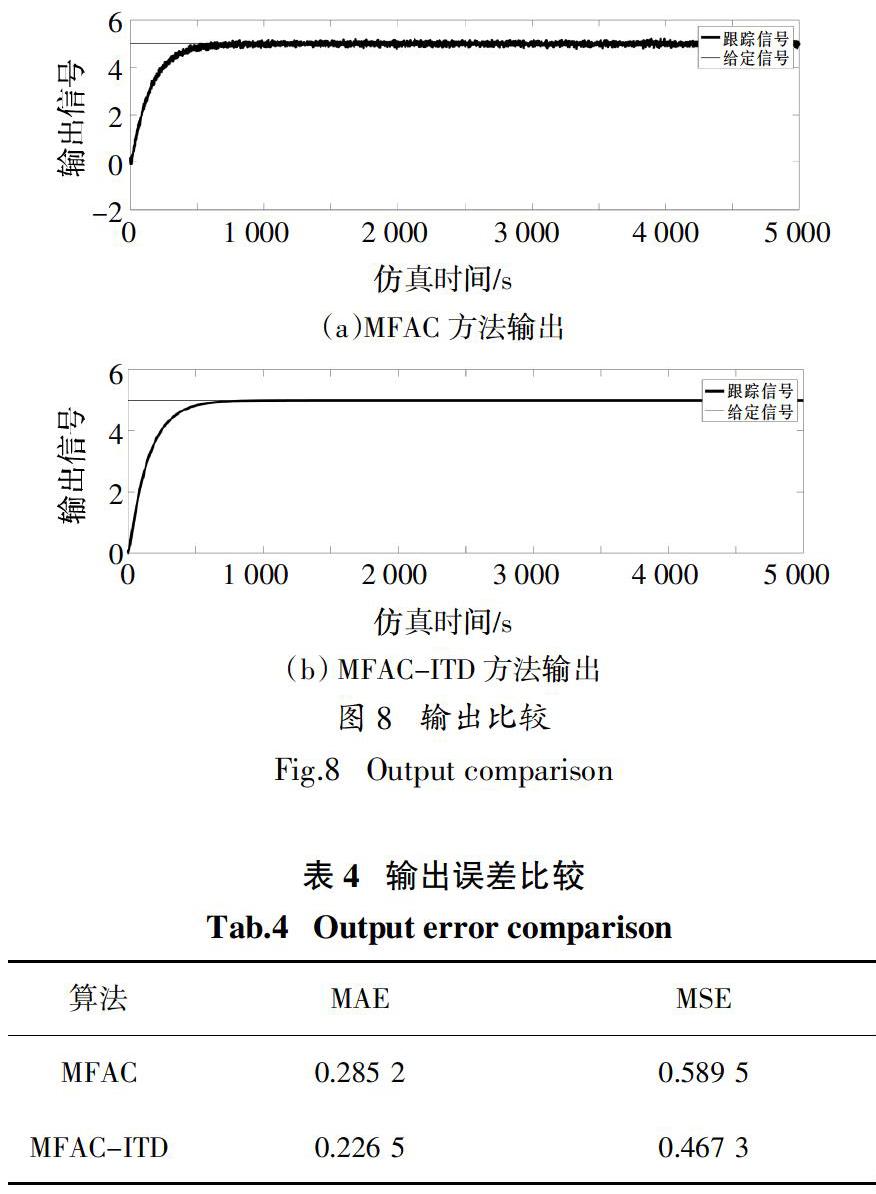
由圖8和表4可以看出，本文提出MFAC-ITD方法有效去除了噪聲帶來的干擾，同時很大程度上保持了MFAC算法的快速跟蹤特性，使得汽包水位保持穩(wěn)定.

4? ?結? ?論

本文針對伴隨噪聲干擾的系統(tǒng)，提出一種基于 改進跟蹤微分器的無模型自適應控制方法，并給出 了相關的收斂性證明，最后將改進的方法應用到 CFB鍋爐汽包水位的控制中，進一步完善了MFAC方法在伴隨噪聲系統(tǒng)中的應用. 同時在不同的仿真環(huán)境下進行了實驗，實驗結果表明：本文提出的 MFAC-ITD方法在不同仿真條件下，輸出誤差的相關指標均遠優(yōu)于MFAC-TD方法，具有響應快速、超調小的特性，將跟蹤速度提高了2～3倍，很大程度保持了MFAC方法快速響應的優(yōu)良特性和魯棒性. 下一步工作將對多輸入輸出系統(tǒng)進行研究.

參考文獻

[1]? ? 沙毅，范倩雯，張立立，等. 自校正模糊PID控制的FAST節(jié)點位移控制方法[J]. 東北大學學報（自然科學版），2018，39（4）：487—491.

SHA Y，F(xiàn)AN Q W，ZHANG L L，et al. FAST node displacement control method using self-tunning fuzzy PID control[J]. Journal of Northeastern University （Natural Science），2018，39（4）：487—491. （In Chinese）

[2]? ? 邱占芝，李世峰. 基于神經網絡的PID網絡化控制系統(tǒng)建模與仿真[J]. 系統(tǒng)仿真學報，2018，30（4）：1423—1432.

QIU Z Z，LI S F. Modeling and simulation of PID networked control systems based on neural network[J]. Journal of System Simulation，2018，30（4）：1423—1432. （In Chinese）

[3]? ? 張凱，張秀清，張黎明，等. 基于改進的同步擾動隨機逼近算法的聚表二元驅優(yōu)化[J]. 中國石油大學學報（自然科學版），2017，41（5）：102—109.

ZHANG K，ZHANG X Q，ZHANG L M，et al. A novel approach for optimization of polymer-surfactant flooding based on simultaneous perturbation stochastic approximation algorithm[J]. Journal of China University of Petroleum （Edition of Natural Science），2017，41（5）：102—109. （In Chinese）

[4]? ? 周穎，何磊，鄭鳳. 具有時延和數(shù)據丟失的直線電機迭代學習控制[J]. 控制理論與應用，2017，34（12）：1631—1636.

ZHOU Y，HE L，ZHENG F. Iterative learning control for linear motor system with time delay and data dropout[J]. Control Theory and Applications，2017，34（12）： 1631—1636. （In Chinese）

[5]? ? CAMPI M C，LECCHINI A，SAVARESI S M. Virtual reference feedback tuning： a direct method for the design of feedback controllers [J]. Automatical，2002，38（8）： 1337—1346.

[6]? ? 侯忠生. 非線性系統(tǒng)參數(shù)辨識、自適應控制及無模型自適應控制[D]. 沈陽：東北大學信息科學與工程學院，1994：26—92.

HOU Z S. Nonlinear system parameter identification，adaptive control and model-free adaptive control[D]. Shenyang： College of Information Science and Engineering，Northeastern University，1994：26—92. （In Chinese）

[7]? ? 侯明冬，王印松. 一種無模型自適應積分終端滑模控制方法[J]. 控制與決策，2018，33（9）：1591—1597.