基于協方差分解法的邊坡可靠度仿真探析

[摘要]邊坡在地球上是一種很常見的現象，這種現象存在一定的不穩定性，它的不穩定性會對工程建設帶來不小的災害。邊坡可靠度分析在路橋工程、工民建工程、市政工程等工程中常常遇到的一個很重要的問題。影響邊坡穩定性的因素就是具有隨機性的問題，用協方差分解法來對隨機場進行分析，可以弄清楚研究對象的各個影響因素之間相互作用對研究對象的影響。

[關鍵詞]邊坡穩定性;蒙特卡洛方法;協方差分解法

[中圖分類號]TU43

[文獻標識碼]B

1緒論

1.1問題的提出

隨著現代技術的發展，建筑工程技術越來越成熟，人類對于土地的使用要也越來越高。在路橋工程，工民建工程，水利水電等工程中，邊坡所帶來的災害也屢見不鮮。因此邊坡穩定性的分析也越來越重要，但是傳統的分析方法并不適用，所以我們需要探索更精確、更科學的方法進行數學和模型仿真分析。

1.2邊坡穩定性分析的方法

最初最常用的方法就是安全系數法，這種方法是將許多不確定的因素概括成為一個確定的安全系數，用這種安全系數作為標準來表示出邊坡的穩定性。經過長期的研究又出現了Fellenius法、Bishop法、Morgenstem-Price法等更高級的方法。但是這些方法卻不能把握住土的隨機性，只是單純的把土看作—個統一的整體來進行研究，把土的材質均勻處理化。但是通過實際的研究發現，土的不穩定因素呈現出隨機性，這使得蒙特卡洛方法在邊坡穩定性研究中取得了重要的作用。蒙特卡洛方法是針對隨機性問題的方法，它可以描述和模擬整個概率過程，通過研究概率數學模型，可以更好的研究邊坡的不穩定性因素。

1.3研究的意義

土質的參數存在很大的隨機性、多變性、復雜性。安全系數研究法不能準確的描述出邊坡的可靠程度，所以需要研究能對隨機數據能進行更好分析的方法。

中國是一個邊坡災害發生大國，每年都會有大大小小的各種滑坡事件發生。這些災害對人們的生命和財產都帶來了巨大的損害，對國家的經濟損害也是巨大的。隨著國力的發展，中國也開始建設更多大型工程，例如：三峽工程、南水北調工程等水利水電工程，還有山體鐵路隧道公路等工程，這些工程使得我們對邊坡可靠度的研究必須做到更準確更透徹。

2正態分布隨機場與MATLAB

2.1蒙特卡羅方法

蒙特卡洛方法是針對具有隨機性的問題的一種方法，這個方法可以描述和模擬整個概率過程。在這個建模中我們所構建的邊坡各項指標是隨機分布的，所以在這里要用到蒙特卡羅方法。首先我們需要建立一個概率模型，這個模型可以看作是由不同的概率分布構成的。實現蒙特卡羅方法必須要有已知概率的隨機變量。而這個隨機變量我們就可以借助MATLAB來實現。在我們這次仿真中，蒙特卡羅方法的具體應用是先生成隨機變量的樣本，再利用可靠度分析中提到的功能函數來統計失效樣本的數量并估計出失效概率。因為輸入的參數是由MATLAB生成的隨機數，所以得到的失效概率也是一個隨機變量所以必須通過反復的運算才能得到安全系數的樣本。計算失效概率的公式如下：p？=l/n，L是通過功能函數所得到的不符合極限要求樣本的次數，n是運算的總次數。

2.2 MATLAB的應用

首先輸入代碼：

clc;clear all;

pf=0.

f=randu（100）

for i=1：10000

if f（i>=0.

pf=pf+1

end

t=pf/10000：

這條命令將隨機生成10000個隨機數。

子函數代碼：

Function main

F=randndn（100）

Sdfety=0

For i=l：10000

Safety=panbie（f，I， safRety）

End

Pf= failure /10000

function failUrte=panbie（f，I. safety）.

if i >0.

safety=safety+1.

end

這條命令是將邊坡可靠度的判別分為了兩個函數，第二個為子函數。

2.3 MATLAB數據的輸入與輸出

在MATLAB的使用過程中我們要將10000個隨機數從MATLAB中導出成為一個dat文件。.也需要將電腦中的dat文件再導入到MATLAB中。所以我們需要用到輸入和輸出語句。下面分別是輸入和輸出的例子。

輸入：

clear

clc

fid_c =fopen（cohesion.dat，w）;

fid._phi=fopen（phi. dat，w）;

mu=[13.8，37];cv=[.2，.2]：

% mu=[1.40];cv=[.1，.1];

sigma=mu.*cv

j=10000.

c=normrnd（mu（1），sigma（1），i，1）：

phi=normrnd（mu（2），sigma（2），i，1）

fprintf（fid_c，%f＼n，c）：

fprintf（fid_phi，%f＼n，phi）：

fclose（fid_c）

fclose（fid_phi）;

這樣子就生成了cohesion和phi兩個文本文檔。成功的將MATLAB生成的數據變成兩個文本文檔。生成這兩個文本文檔是為了便于后面的應用。

輸出：

clear all：

clc

% fid_c=fopen（cohesion.dat，r）：

% fid_phi=fopen（phi. dat，r）：

c1=csvread（D：＼MATLAB7＼bp680＼cohesion1.dat）：

c2=csvread（D：＼MATLAB7＼bp680＼cohesion2.dat）：

phi2=csvread（D：＼MATLAB7＼bp680＼phi2.dat）：

fos=csvread（D：＼MATLAB7＼bp680＼pos680.dat）：

% fclose（fid_c）：

% fclose（fid_phi）

這條命令可以直接將上面剛剛保存的兩個文檔直接替換到MATLAB中來Fid是指定要寫入的數據文件cohesion和phi是文件名r是用只讀方式打開。

3隨機場理論與FLAC建模及應用

3.1隨機場理論

我們的研究中只考慮到土的cohesion和phi性質，所以在這里用隨機場來模擬土的性質是符合現實情況的。

協方差函數是隨機場的數字特征，本次主要研究的就是協方差法在邊坡可靠度仿真中的作用。

土性指標一般是由試樣的測值來反映的。土的空間平均性質有兩層意義：一是土性參數是個隨機變量，而且是一個空間內的隨機變量，隨位置的變化而變化;二是土的極限狀態取決于土性在空間中的分布情況。

我們可以將士的性質視為依賴于土體并且隨不同位置而變化的隨機變量，是在空間上分布的隨機場。所以我們要弄清楚隨機場的性質，這樣我們就可以把邊坡的可靠度問題轉化為一個隨機變量的問題。

在本文中我們將用半變異函數理論。半變異函數理論被廣泛的用于礦體的品位及儲量的估計。具體理論如下：

將單位空間∞中的土的性質參數看作具有一定關聯的變量。將土體中某一點t的參數隨機變量設為X（t），那么x（t）與x（t+τ）的相關特陛可以表示為下式：

r（τ）=1/2var[X（t）-X（t+τ）]=1/2E{X（t）-X（t+τ）]2}

其估計量為：r*（τ）=1/2N（τ）ΣN（τ） i=1 [X（ti）-X（ti+τ）]2

N（τ）為以向量τ相隔的試驗數據對x（t）與x（t+τ）的數目。

變異函數有很多種模型，我們所用到的有指數模型和高斯模型，其表達式為：

指數模型：r（h）=1-exp（-ah）

高斯模型：r（h）=1-exp（-a2h2）

式子中，Co為塊金值;C為基臺值;a為相關距離。

在后面的MATLABCUIDE設計中我們將要用到這個隨機場理論，并且用這個理論進行模擬和建模。

3.2協方差函數

設隨機場[y（z）]的二維聯合函數為Fz1z2（x1x2），則對任意z1，z2∈Z，隨機場[y（z）]的協方差函數定義為：

CYY（z1z2）=E{[y（z1）-E{y（z1）}][y（z1）-E{y（z2）}]}

=[x1-Ey（z1）}][x2-E{y（z1}]dFz1z2（x1，x2）

協方差函數CYY（z1，z1）實質上是y（z1）和y（z2）的二階混合中心距。它是參數z1、z2的二元函數。小標的作用是表示其是隨機場[y（z）]的協方差函數。記為CY（z1，z2）。

在研究中使用的協方差分解法：先直接生成一個隨機場。如果隨機場z（t）被劃分為n個網格點，那么協方差矩陣Cn×n就由Ci，j=C（ti，tj）元素組成（i=1，2，…，n

j=1，2，…，n）。因此，平穩高斯隨機場可以表示為下式：

Cn×n=Ln×nLn×n T Gn×1=Ln×nWn×1

LLT是協方差矩陣C中的喬里斯基分解矩陣，W是一個獨立的向量，是分布在N（0，1）里的隨機數，Gn×1是構成離散化高斯平穩隨機場的隨機變量gi，i=1，2，…，n的向量。

3.3 FLAC建模

首先我們用FLAC建立一個邊坡的模型例如圖1所示。

我們需要建立一個與之類似的模型，并且將cohesion和phi這兩個變量隨機分布到這個邊坡中，使整個邊坡的結構變得隨機化，從而便于計算邊坡的可靠度。

3.4邊坡可靠度算例

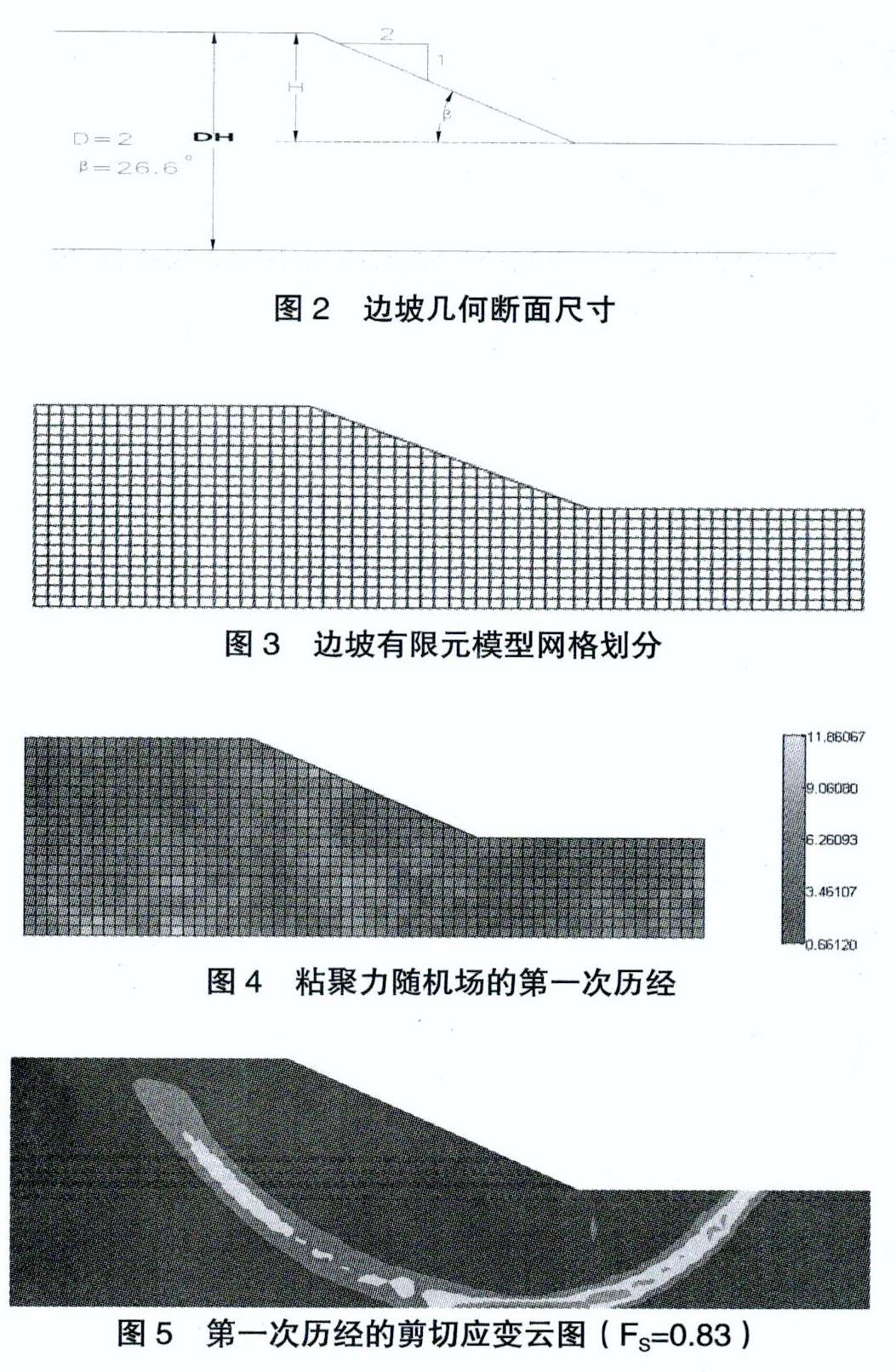
我們這里采用如下的邊坡算例來說明前面方法的有效性。在算例中邊坡的幾何尺寸如圖2所示，邊坡的有限元模型剖分為910個單元，如圖3所示。邊坡的容重為20kN/m3，泊松比為0.3。彈模為1.0?105kN/m2。土的摩擦角和膨脹角均取0。假定粘聚力cn為平穩隨機場，其統計特征為均值5kN/m2，變異系數為0.5，相關長度為1m的指數型相關函數。圖4給出了粘聚力隨機場的第一次歷經。圖5給出了第一次歷經所對應的邊坡失效形式。此時邊坡安全系數為0.83。彈塑性變形產生了貫通的剪切面。

4結論

由于邊坡次生災害頻發，邊坡可靠度也成了一個在國際上關注度很高的重大問題，對于邊坡防治的工程朝著更加準確更加實用更加便捷的方向在發展，特別是伴隨計算機的越加普及，讓邊坡穩定性分析的方法發生了質的變化，并且走向了一個新的方向。我們所研究的就是利用MATLAB和FLAC編程來進行邊坡可靠度模型仿真，利用計算機的強大處理能力進行高達上萬次的模擬和計算，得出一個準確的可靠度數據。

這個方法的基本理論支持是蒙特卡洛方法，通過對隨機場的模擬和演算，我們可以模擬出最符合實際情況的土性質參數。

這個方法比傳統的安全系數法更加準確，操作起來更加方便，演算過程由計算機控制，大大減少了計算的工程量。數據具有隨機性，大大的提高了準確度。

這個方法的優點很明顯：一是數據更具有隨機性，更加符合實際;二是計算過程簡單;三是由FLAC生成的仿真模型更加直觀。四是操作方便，工程量小。

目前此方法還沒有得到普及，但是隨著計算機應用的越發成熟，以及我們對邊坡研究的越發深刻，基于協方差分解法的邊坡可靠度仿真將得到越來越廣泛的應用。

[參考文獻]

[1]劉波，韓彥輝.FLAC原理實例與應用指南[M].北京：人民交通出版社，2005.

[2]陳育民，徐鼎平.FLAC/FLAC3D基礎與工程實例[M].北京：中國水利水電出版社，2009.

[3]高謙，王思敬.龍灘水電站船閘高邊坡的可靠度分析[J].，石力學與工程學報，1991，10（1）：83-95.

[4]邱賢德，高先良，袁德順，等.礦山邊坡可靠度分析的研究[J].化工礦山技術，1998，27（1）：2-10.

[5]李俊，彭振斌，周斌，利用有理多項式技術計算基于Bishop分析模式的邊坡穩定可靠度[J].合肥工業大學學報（自然科學版），2009，32（4）：519-522.

[6]趙尚毅，鄭穎人，鄧衛東.用有限元強度折減法進行節理巖質邊坡穩定性分析[J].巖石力學與工程學報，2003，22（2）：254-260.

[收稿日期]2020-08-31

[作者簡介]王冠（1993-），男，湖北武漢人，助理工程師，研究方向：建筑工程預決算。