分類問題中的算法

李曉明

現在，人工智能很熱。人工智能應用中有些很基本的需求，分類即為其中最常見的一種。分類關心的是如何將一個對象歸到已知類別中。例如，人可以分為少年、青年、中年、老年四個類別，商品可以分為廉價和高檔兩個類別，學生在課堂上的表現可分為積極踴躍、沉穩細致、不以為然三個類別，網購者可分為隨性和理性兩種類別，等等。在日常生活中，這種分類主要憑感覺。而如果用計算機來做，則每一種類別都需要通過一些數據特征予以刻畫，每一個對象或者說個體都是通過一個“數據點”來表示，如后面要講的一個網購的例子，其數據特征就用了“每月網購次數”和“每次平均花費”。一個每月網購10次、每次平均花費120元的人則用數據點（10，120）來表示。

不難體會到，把一個個體歸到預設的類別中，有些比較容易，有些則很不容易。鑒于分類在現實中有廣泛的應用，人們發明了多種算法，應對各種不同的情形。本文介紹兩個最基本的算法——K近鄰（KNN）算法和支持向量機（SVM）算法。

這兩個算法的基本思路都很簡單直觀。KNN的實現容易理解，因而人工智能的教材里一般都會有它。SVM的常規實現需要較深的數學基礎，因而一般初等人工智能教材都沒有它。不過，由于SVM實在很重要，最近也看到有嘗試在中學人工智能教材中介紹它[1]，只是在介紹了算法基本思想后用了一句“這個問題可以用優化方法求解，但具體過程已經超出了同學們現階段的知識儲備，等到同學們以后學習了相關的數學工具后，就可以求解了”就結束了。本文將從一個不同的視角描述一個實現SVM的算法，該算法從效率上講沒有常規的SVM算法高，但用到的數學知識在中學生可理解的范疇內，他們應該能夠編程實現，因而適合中學的教學。

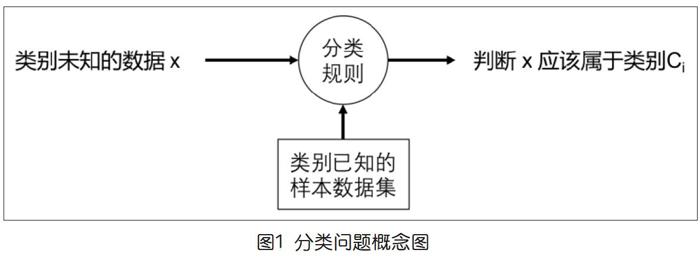
一般而言，設計分類算法的目的是實現一個所謂“分類器”（程序）。分類器的實現通常都是基于一批已知類別的數據，形成某些規則，來做未知類別對象的類別判斷，圖1是一個概念圖。

實現一個分類器的基礎是一個預先給定的類別集合C={C1，C2，...，Cm}和一批已知類別的樣本數據集D={d1，d2，...，dn}。不同分類算法的區別一般體現在所形成的分類規則上。

類別集合C通常是人們根據需要或經驗事先確定的，有一定現實含義，如本文開始時提到的那些。樣本數據集D怎么做到類別已知的呢？通常是采用人工標注給定，也就是事先找來一批有代表性的數據，請有背景知識的人一一給打上類別標簽。這項工作一方面很重要，對后續自動分類的質量有基礎性影響，另一方面在互聯網經濟中的需求越來越普遍，因而形成了一種新職業——數據標注員。

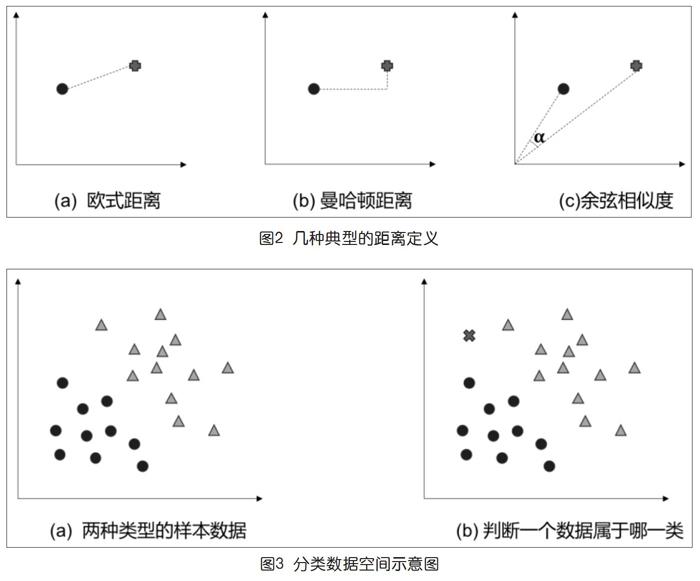
在分類問題中，一個核心的概念是兩個數據點之間的距離。所謂判斷一個數據點該屬于哪個類，本質上就是看它離哪個類的已知數據點更近。而“距離”在不同的應用背景下可能有不同的定義。我們以二維數據空間為例，給出三種常見的距離定義，如圖2所示。

設（x1，y1）和（x2，y2）為兩個數據點p1和p2的坐標，歐式距離、曼哈頓距離和余弦相似度①分別為：

其中，前面兩個都有“數值越小越接近（相似）”的含義，而余弦相似度定義在區間[0，1]，越大越相似。若余弦相似度為1，意味著兩個數據點同在一條通過原點的直線上。體會這幾個定義的含義，讀者對它們適用的不同場合能有些直覺認識。

一般而言，KNN和SVM處理的數據點都可以是高維的，用多于三個特征分量來表示一個對象的特征。本文為突出要點，只考慮二維的情形，于是有如圖3所示的視覺形象，便于解釋有關細節。

圖3（a）示意在二維數據空間中有兩種已經標注（分別用圓和三角表示）類型的樣本數據。它們大致分布在空間中兩個不同的區域，任何兩個數據點之間都可以談論某種距離。我們特別注意到，同類數據之間的距離不一定就比異類之間的小。圖3（b）示意出現了一個未知類別的數據（x），它應該屬于哪一類呢？

● KNN算法基本思路

針對樣本數據D，KNN算法采用了一種可以說是體現“近朱者赤，近墨者黑”和“少數服從多數”原則的直截了當的思路。它一一計算待分類數據x與樣本數據集D中所有數據的距離，然后取其中最小的K個（也就是“KNN”中的K，而NN表示“最近的鄰點”），看它們分別屬于哪一個類，判定x應該屬于K中出現較多的那個類。

采用什么距離定義和具體應用有關，為和后面的例子對應，下面的算法描述采用了余弦相似度作為距離。

● KNN分類算法（如表1）

● 算法運行例

假設我們考慮對網購者的分類，用“每月網購次數”和“每次平均花費”兩個量來刻畫每一個用戶，要看一個人是“隨性”（S）還是“理性”（R）②。有一個已經人工標好類型的樣本數據如圖4（a）所示，現在有一個用戶每月網購5次，平均花費40元，即她的數據是x=（5，40）。問她是屬于隨性網購者還是理性網購者？

采用KNN算法對這個用戶分類，采用余弦相似度作為距離度量，首先算得x=（4，50）與16個已知數據的距離，如圖4（b）第1列所示。為方便查看，我們把那些距離按照與1接近的程度的排序放在表中最右邊一列。（注意，對余弦距離而言，越接近1表示越“近”）

現在，如果取K=1，看到離x最近的（6，45）是“S”，于是x應該被分類為“S”。如果取K=3，離x最近的3個都是“S”，如果取K=5，離x最近的5個里有4個“S”1個“R”，等等。你覺得應該認為x是隨性網購者還是理性網購者呢？顯然，認為這個x是一個隨性網購者比較合理。

● 算法性質的分析

這是一個正確的算法嗎？如果考慮的是2-分類，即類別數為2，且K為奇數，KNN算法總會有一個輸出，建議x應該屬于哪一類。因此不存在停機或收斂之類的問題。問題可能在于它給出的建議到底有多靠譜。這樣，除了給出x當屬于哪個類別外，還可以給出一個概率，即在TOP-K中，占優類型的數據在整個K中的占比。例如，在上面的例子中，K=3，這個占比就是100%，K=5，這個占比就是80%。如果類別數大于2，則還需要有一個方法來做“平手消解”，當某兩類在TOP-K中有相同出現時決定取哪一個。

一個分類器的質量常常用“準確度”（accuracy）指標來評價。假設一共有p個測試數據x1，x2，…，xp，對它們分完類后人工一一做檢查。用r表示分類錯誤的個數，準確度就是p/（p+r）。

這個算法的效率如何呢？

KNN分類算法的計算復雜度與樣本集大小（n）有關，與樣本屬性的維數有關。在我們討論的二維情況下，從算法描述中可以看到，計算余弦距離時間復雜度是O（n）。算法第3行找出n個相似度中的TOP-K，一般算法是O（k*n），采用適當的數據結構可以做到O（k*logn）。

在學過了算法園地專欄前面十多個算法后，現在學KNN算法，讀者可能會產生一種十分不一樣的感覺。首先，這種算法看起來好簡單，直截了當好理解，其邏輯與前面討論過的那些相比要淺顯許多。其次，給出的分類結果到底有多靠譜，一般來說是沒法證明的。事實上，像分類這樣的問題，現實中經常就是沒有客觀標準。但為了能推進研究，人們通常會準備一些有代表性的測試數據集（benchmark）用于比較不同方法的效果。當然，最終效果如何，只能通過實際應用檢驗了。

● SVM概念與算法目標

下面討論SVM，它有一個聽起來很高深的名字“支持向量機”。我們不被它困擾，來看具體是什么意思。還是用圖3的數據，畫出SVM分類概念的示意圖，如圖5（a）所示。

可以看到，圖中除了數據點，還有將兩類數據點分開的直線。SVM就是要基于樣本數據點，算出一條那樣的直線（y=ax+b），從而可對擬分類數據依照它是在直線的左右來賦予類別，這個示例就是左邊為“圓”，右邊為“三角”。不過，讀者可能馬上注意到圖5（a）中有兩條直線，它們對于待分類數據點（x）分類的結論是不同的，于是就有了哪個更好的問題。SVM怎么考慮呢？SVM要求一條“最優的”直線。

什么叫“最優的”直線？SVM采用的觀點是離它最近的數據點盡量遠。形象地看，就是在兩類數據之間“最窄”處的中線。圖5（b）是一個示意，根據兩類數據點的情況，我們分別畫了一個外包凸多邊形（這種多邊形在計算幾何學中叫“凸包”），這樣它們之間的“通道”也看得很清楚了③。如果我們能確定兩個凸包上距離最近的兩個點（不一定都恰好在頂點上），做連接它們的線段，再做該線段的垂直平分線，就得到了SVM的結果，如圖5（c）所示。

下面給出的SVM算法就是求這樣一條直線的算法。讀者能感到與前面的KNN很不同，那里是基于樣本數據直接對數據點（x）做分類。不過，讀者也能意識到，一旦有了這樣一條直線，判斷一個數據（x）應該屬于哪一類就是一件平凡的事情，用不著專門說了。

● 一種SVM分類器算法

下面描述的算法相對比較宏觀（如表2），有利于讀者把握整體概念。其中的細節在后面做進一步闡述。另外，所提到的距離此時均為歐幾里德距離。

下面來討論其中的要點。首先，理解這個算法的細節（包括編程實現）所需的主要數學知識為平面向量的知識，這在高中新教材中已有覆蓋，見參考文獻[2]的第6章。具體包括平面上兩個點的距離公式、一個點到一條直線的距離公式（由此得到點到線段的距離公式）、根據一個點的坐標和斜率確定直線y=ax+b的方法等。下面以算法中的最后一步（5）為例，展示處理這類問題的樣式。已知由（x1，y1）和（x2，y2）確定的線段，要確定垂直平分線y=ax+b中的參數a和b。

算法的第2、3、4步只涉及距離的計算和排序，不用贅述。算法的第1步，從一個平面數據點集得到它的凸包。這是計算幾何學中的一種基本運算，人們研究出了許多簡單易懂的算法，陳道蓄教授在本專欄上一期，也就是2020年第21期上介紹了其中兩種[3]，在此也不贅述，有興趣的讀者可自行查閱學習。

● 算法的性質分析

先看計算復雜性。若第1步采用[3]中介紹的第二個算法，復雜性是O（nlogn）。第2步和第3步計算距離，若不采用任何優化，為O（n2）。第4和第5步是常數時間。總的來說，復雜性為O（n2）。

為什么算法得到的直線y=ax+b就是最優的一條直線？由于它是在兩個最短距離的點（x1，y1）和（x2，y2）之間，這意味著兩類數據之間不可能有更寬的通道。而由于它是“垂直平分線”，這意味著它做到了讓“離它最近的數據點盡量遠”。

不過，細心的讀者可能問到一個更加微妙的問題。那就是，記即數據點（? ? ? ）和（? ? ? ）之間線段的長度，那么兩個數據點離上述直線的距離都是d/2。為什么樣本數據中不可能有其他的數據點，離直線的距離小于d/2呢？這與凸包的性質有關，與直線是“垂直平分線”有關，也與算法中第3步強調了要包括“點與邊的距離”有關。鼓勵有興趣的讀者思考體會一下這背后的“玄機”。當然，也歡迎有疑問的讀者與我們交流。

本文形成過程中與陳道蓄教授有過深入討論，他指出SVM算法中的第2步可以省去，進而第4步也可以省去了。想想的確如此。不過文中保留了原樣，留作讀者思考為什么那兩步可以省去。

釋：①即平面上兩個向量夾角的余弦值，其表達式的推導可見高中數學教材[2]。

②用什么特征來表示所關心的類型，與對應用背景的理解直接相關。這里采用兩個特征分量只是用來說明算法運行的過程，實際應用中為區分隨性和理性消費者會比這要求更多。

③這里，我們總假設兩個凸多邊形是不重疊的。

參考文獻：

[1]湯曉鷗，陳玉琨.人工智能基礎（高中版）[M].上海：華東師范大學出版社，2018，4：35.

[2]薛彬，張淑梅.數學（第二冊）[M].北京：人民教育出版社，2019，7：34.

[3]陳道蓄.平面上的凸包計算[J].中國信息技術教育，2020（21）：25-29.

注：作者系北京大學計算機系原系主任。