從模型到現實

陳凱

科學研究的過程，一般是從觀察和發現問題開始，針對問題給出猜想和假設，接下來是設計實驗或者設置進一步觀察的任務，借由實驗和進一步的觀察，對數據結果進行分析，給出理論上的解釋或者建立能反映事物變化的模型。為了驗證理論或模型的可靠性，常需要對未知的現象進行預測，預測的成功則驗證了理論或模型在特定范圍內具有一定的可靠性。

在人工智能高度發展的今天，筆者希望能找到一些能夠用于基礎教育階段課堂的案例，用以展現機器學習在科學研究過程中模型建立與未知事物預測方面可能起到的作用。筆者抱有這樣的愿望：模型建立中的數據是由學生親自觀察、采集并記錄下來的，這些數據雖然數量不少，但精度略有不足（這恰恰反映了現實中最可能的情況）;模型本身能由相對簡單的數學公式或動力學系統構成，能夠適應基礎教育階段學生的知識技能水平;模型構造的過程能夠體現機器學習算法的參與，算法原理簡單，算法實現工具相對便捷。

本文給出的“木星衛星軌道數據的分析和智能預測”案例，正是為實現上述目標而設計的，整個教學過程需要多個課時，包括：①問題發現：由望遠鏡觀察注意到木星臨近的未知天體;②建立假設：猜測這些天體實際是圍繞木星旋轉的衛星，并給出假設的依據;③設置觀察任務并建立數學模型：觀察并作數據記錄，根據假設，按正弦函數建立數學模型對數據進行匹配，這里的函數擬合需求引出了機器學習算法;④優化模型構建過程：為優化函數擬合的方法，討論可能用到的機器學習算法的種類并對其基本原理進行介紹;⑤進行預測：根據機器學習算法完成程序代碼，并用其預測未來天體運行情況。限于篇幅，本文重點討論第③點，在學習者尚不具備較完整編程能力的情況下，可用電子表格來進行數據處理并呈現出對于機器學習算法的需求，這樣就擴展了該案例的適用學習對象。

● 玩一個和正弦函數有關的游戲

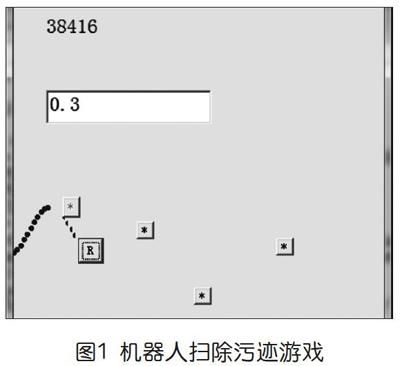
向學習者推薦一個機器人擦地板去除污跡的游戲，游戲任務是：如圖1所示，某種型號的機器人均按正弦函數曲線的樣式在地板上行進，某故障機器人在行進路線上隨機殘留下了油污，現派出清理機器人按正弦函數曲線在地板上行進并抹除地板上的污跡，但清理機器人并不知道故障機器人所采用正弦函數曲線的周期是多少，清理過程中也不可中途更正正弦函數周期，為達到最好的抹除污跡的效果，玩家可以隨機在文本框內輸入正弦函數周期倍數，然后觀察該機器人除污的效果。在機器人實施任務的過程中，還可以觀察它離污跡的距離有多遠。

引入這個小游戲的目的，是用游戲作為一個模型，在直觀的行為變化和抽象的數學函數兩者之間建立起聯系。學習者在游戲的交互過程中，熟悉不同的周期倍數所對應的函數圖形形態。

● 給出建立數學模型的需求

機器人除污的游戲正好對應木星衛星軌道的預測問題，兩者所使用到的數學模型是完全相同的，以下選用日常觀察和記錄最為方便的木衛三來舉例說明：若以時間為橫軸，以望遠鏡觀測到的木衛三離開木星距離的數據（以比例方式記錄）在縱軸上畫點，便能得到一系列的散點。由于天氣等因素的影響，這些散點從時間軸方向看是分布不均的，又由于觀察和記錄必然存在誤差，所以在縱軸上點的位置也并不完全精確，從科學研究的角度看，若假設木星衛星是圍繞木星旋轉的，則可以假設如能觀察到任意時間點的距離，則可將這些散點連成一個接近正弦函數的曲線（木衛三的運動軌跡為一個非常接近圓形的橢圓，從運行軌道側面觀察，按時間軸方向采集距離數據，就能描繪得到近乎正弦函數的曲線，關于何以導致特定偏心率，這涉及具體的物理學問題，這里不進一步展開）。只要確定正弦函數的周期倍數，就能夠為木星衛星的運行在視場中的位置變化建立數學模型。

雖然木衛三位置預測問題和機器人除污問題本質上是同一個問題，但其中，機器人除污問題直接和數學模型有著對應關系，而對于木衛三位置預測問題，卻要經歷將現實中的問題轉換成數學問題的過程，所以在教學過程中，將機器人除污問題作為一個中介，在思維上把現實問題和數學模型連接起來（如表1）。

● 數學模型的建立

無論是機器人除污，還是木衛三位置預測，它們用到的數學模型都只是簡單的正弦函數，其中僅有一個變量即周期倍數，如何找到這個周期倍數呢？先考慮一種簡單的處理方法，先任意地隨機取一個周期倍數，用該周期繪制出正弦函數的曲線，觀察其與期望坐標點匹配的程度。以機器人除污游戲為例，觀察并記錄該機器人在行進過程中，當其與污跡在橫軸上處于同一位置時，在縱軸上的差距有多少，然后不斷調整周期倍數，試圖找出更小的差距。那么，應該遵循何種策略調整周期倍數呢？似乎可以用如下方法，略增加或略減小周期倍數，用新的周期倍數繪制出正弦函數曲線，并計算該機器人與污跡在縱軸上的差距是否有所減少。如差距有所減少，則繼續按此方向修改數據，直到在此方向上修改數據會導致差距反而增加時停止。以上探索過程使用電子表格就能夠呈現出來，也可用Python等程序語言來模擬。

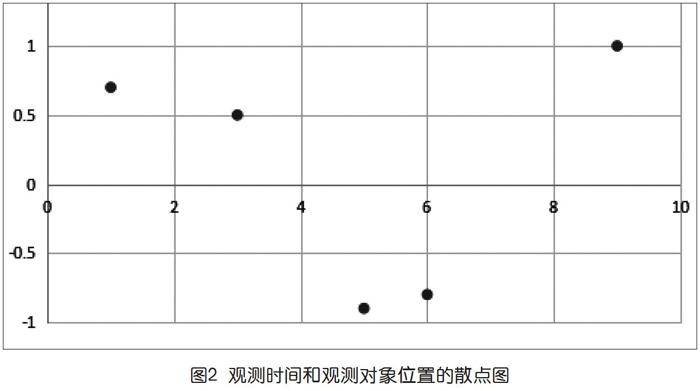
然而，上面的方法未必能得到最優的結果。為了看出這個方法的局限性，下面用木衛三觀測數據舉例（為論述簡單起見，表中已將距離數值折算為比例），如上頁表2所示。

假設取前5個觀測值，將觀測序號作為橫軸坐標點位置，木衛三和木星距離的比例為縱軸坐標點位置，則得到的圖像如圖2所示。

由于不知道正弦函數周期倍數，可以隨機取值進行試探，假設取周期倍數為125，則獲得正弦函數為sin（125*x*3.14/180），這個函數是不是能很好地擬合散點圖中的觀測點呢？用一個數學公式就可以知道：

Fitness

=ABS（SIN（125*1*3.14/180）-0.7）+ABS（SIN（125*3*3.14/180）-0.5）+ABS（SIN（125*5*3.14/180）+0.9）+ABS（SIN（125*6*3.14/180）+0.8）+ABS（SIN（125*9*3.14/180）-1）

公式乍一看有些復雜，其實就是將周期倍數為125的正弦函數，獲得其橫軸在1、3、5、6、9處的縱軸坐標值，將其與觀測到的散點的縱軸坐標值相減，取絕對值后相加，這樣可以看出隨機選擇的周期倍數離理想的擬合曲線的差距到底有多少，上述公式計算結果是2.054。因為可以根據此數值判定隨機猜測的優劣，所以將其稱為正弦函數擬合的適應性公式。

如再取倍數126，則該適應性公式的差值數據會減少，可看作是離理想的倍數更近一步，可發現，倍數在大約130時，差值降低到最小，然后差值又將變大，所以可以推測，正弦函數的周期倍數是130。但這個結論是錯誤的，因為最低點的橫坐標軸大概在橫軸坐標50處，因此可知木衛三運行軌道可完美匹配周期倍數為50的正弦函數，則可證明木衛三確實按近圓形軌道圍繞木星運動。另外，因為50大約是360的七分之一，所以可推測木衛三公轉周期約為七天。由此，就可以對下一周某天的木衛三出現的位置進行預測了。

● 從人腦判斷到機器判斷

由于繪制出了不同周期倍數所對應的適應性情況的結果，人腦可直觀把握圖形所表達的意義，并幾乎立刻能找到曲線最低點，但一般的程序設計語言卻不具備直觀的能力（這里不展開討論并行處理系統）。在電子表格實驗中，選取了250個點得到了曲線，如果曲線更復雜，則采樣點勢必要增加。而在其他類似尋找函數極值的問題中，如若影響曲線變化的變量大幅增加，那么繪圖工作就由二維平面擴展到更高維的空間，這樣不僅會導致數據量極大增加，而且難以單純靠視覺直觀或程序一一枚舉尋找到極值點。

這個問題很鮮明地將機器運算在整體性和直觀性方面的局限性展現了出來，也就自然而然引出了對機器學習算法的需求。如何為機器設計一個方案，使之能夠在缺乏全局視野的情況下，找出適應性函數曲線的最低點？在這里，就又可以用機器人思維模型（游戲）的形式，對可能的解決方案進行討論，可以將函數波形想象成山巒，思考機器人如何找到海拔最低點。如果教師直接拋出機器學習算法方案，未免浪費了激發學生自主思考和探索的大好機會，所以不妨對思維模型的建立開展頭腦風暴。例如，派出幾千個機器人，隨機占據山的不同位置，將這個過程重復許多次，就能通過排序找出最低點，這個方案顯然太低效了。要想提高機器人的工作效率，就需要改變機器人的工作模式，為機器人設立恰當的運作規則。為解決函數極值問題，常用的方法有模擬退火算法、遺傳算法、粒子群算法等，部分教師很可能對這些算法的使用已比較熟悉，其中部分算法的教學策略，在后續的文章中還會涉及，在正式講授機器學習算法之前，可以利用思維模型（游戲），將機器人實施探索工作的規則和流程，用語言描述出來。有意思的是，判別這些思維上的模型可行與否的一個方法，是尋找這些模型在其自然界的對應事件，因為漫長的時間為萬事萬物的發展變化篩選出了有效的方法。

至此，可以看出教學過程中，模型的不同作用：其一，數學模型是一個預測系統，它對已有數據進行歸納，通過函數擬合對未來事物變化狀況進行預測，這是本案例學習階段3的重點;其二，要想構建起數學模型，可以使用直觀的方法，而若要將這個構建過程變得自動化，可以借助不同的機器學習算法，而許多機器學習算法，實際上也是觀察和模擬自然界復雜現象變化后簡化得到的模型，這是本案例學習階段4的重點。仔細觀察其中的聯系可知：優化數學模型的構建過程，需要信息技術工具的介入，這里強調的是信息技術工具之所用;而一些機器學習算法借鑒模擬了自然世界中的現象變化過程，借助不同方法實現了這種模擬的自動化，這里強調的是信息技術工具之所成。

而貫穿教學過程的機器人除污游戲也是一個模型，其作用與上述模型不同，該游戲一方面對應著有著物質實體的機器人除污系統，另一方面對應著數學上的正弦函數曲線，這樣就成為連接客觀現實和數學抽象的中介，通過動態直觀的展示提高了認識的效率。但其意義不僅僅限于教學法，在后續機器學習算法的教學中，可以鼓勵學習者模仿機器人除污游戲，自行主動建立起用于聯系客觀現實和抽象數學的思維模型。