基于數學史視角下的雙曲線及其標準方程教學設計

陸文婷 韋宏

[摘 要]在數學史視角下可以向我們揭開數學概念、數學思想、數學問題等知識發生和發展的過程。通過數學史融入數學教學，將概念起源和歷史向學生展示清楚，不僅可以促進學生對數學概念的深刻認識，而且能把數學文化與教學活動有效結合起來。

[關鍵詞]數學史;雙曲線;雙曲線方程;數學文化

[作者簡介]陸文婷（1999—），女，廣西欽州人，南寧師范大學2019級數學與統計學院碩士研究生，研究方向為學科教學（數學）;韋 宏（1968—），男，廣西上林人，碩士研究生導師，南寧師范大學數學與統計學院副教授，主要從事學科教學（數學）研究。

[中圖分類號] G640[文獻標識碼] A[文章編號] 1674-9324（2020）45-0-02[收稿日期] 2020-05-14

《普通高中數學課程標準（2017年版）》中明確指出：“數學文化應融入數學教學活動。在教學活動中，教師應有意識地結合相應的教學內容，將數學文化融入教學，有利于激發學生的數學學習興趣，有利于開拓學生的視野、提升數學學科核心素養。”

在以往的雙曲線教學中，學生按照老師的要求直接模仿橢圓概念得出雙曲線的概念、標準方程以及性質，但是這樣學生并不明白雙曲線概念的本質。將數學史融入數學概念教學不僅有利于學生理解數學概念的形成過程，而且能提升學生對數學文化的認同感，彰顯數學的育人價值。本文以雙曲線及其標準方程的教學設計為例進行分析。

一、教學目標

本節課的教學目標是：一是學生能夠理解雙曲線的有關概念，掌握雙曲線定義的代數形式。二是學生經歷分析、歸納、推理和類比的探究雙曲線方程過程。三是學生體驗數學文化的人文價值和應用價值。

二、數學史融入設想材料選擇

圓錐曲線是最先研究為了解決數學“倍立方問題”而引起的。門奈赫莫斯曾經用了兩種方法解決了“倍立方問題”，與此也就發現了圓錐曲線。阿波羅尼奧斯在前人的基礎上繼續研究了圓錐曲線得到了許多圓錐曲線的性質，這些研究成果也就是他的著作《圓錐曲線論》。由于在其著作中關于雙曲線的定義正是現在教材中的標準定義及其有關性質的證明符合學生的幾何水平，所以本文采用阿波羅尼奧斯的雙曲線產生與定義證明的數學史來融入雙曲線教學。通過經歷歷史上對雙曲線探索向學生揭示曲線本質，即平面內到定點的距離與定長關系。抓住了本質，學生在探索雙曲線時就可以追溯數學定理、法則。本文以數學史融入雙曲線概念教學為例，培養學生追溯數學定理、法則能力和解決問題能力，從而在概念教學中滲入核心素養，有助于學生在后續數學的學習起到重要的作用。

三、教學過程設計

（一）復習舊知引入，設置問題驅動

教師引導學生回憶橢圓的定義、標準方程及其性質并提出問題（1）：我們知道橢圓是由一個平面截一個圓錐得到的，有沒有其他方式去截圓錐？并引導學生討論。

師生活動：教師展示平面和圓錐的圖片，學生嘗試利用圖片和空間想象能力找出不同于橢圓的截線并互相交流。然后，教師引導學生將平面與不過頂點且與底面相交的圓錐相截，并得到結論：所截得到的截線不同于橢圓的一個弧形線。

設計意圖：復習橢圓的相關知識，可以為后續的雙曲線做對比鋪墊。學生通過探究截線的過程可以發展他們的空間想象和思維發散能力，同時也讓學生明白為什么要學習這個知識，是因為發現圓錐被不同位置的截面可以產生不同的截線。

（二）概念形成，符號定義

1.推廣切割，引出概念。教師將問題（1）推廣到其他情形，把截一個圓錐改成截兩個對頂的圓錐，出示問題（2）。

問題（2）：用剛才的截法去截兩個對頂的圓錐會得到什么樣的圖形？

師生活動：基于問題（1）的做法，教師引導學生將平面與不過頂點且與底面相交的兩個圓錐相截得到的截線就是今天要學習的雙曲線。

然后，教師指出這種截面得到的圖形的方法其實由來已久，并向學生介紹阿波羅尼奧斯的故事和用幾何畫板展示平面截圓錐的動態過程：

阿波羅尼奧斯對圓錐曲線研究成果寫成一本著作《圓錐曲線論》。其中問題（1）中的截線被阿波羅尼奧斯稱為超曲線，也就是今天“雙曲線的一支”。問題（2）中截線是超曲線，這樣的兩條截線被稱為是“二相對截線”，也就是今天的雙曲線。而“雙曲線”這個名字是由我國清代數學家李善蘭在其著作《代微積拾級》翻譯過來的。

設計意圖：問題（1）的探究得到了雙曲線的一支，問題（2）得到的是今天教材的雙曲線。問題探究讓學生經歷雙曲線知識的產生過程，引入數學史是學生體驗數學文化的人文價值。借助幾何畫板來動態向學生展示平面截圓錐得到的雙曲線截線，使學生深刻感受雙曲線的幾何表征。

2.提出猜想，推理驗證。問題（3）：對于得到的雙曲線，你想研究它的什么？

師生活動：學生模仿已學過的橢圓相關性質來探究雙曲線的性質。教師引導學生討論后，介紹阿波羅尼奧斯研究雙曲線的性質并和學生一起證明。

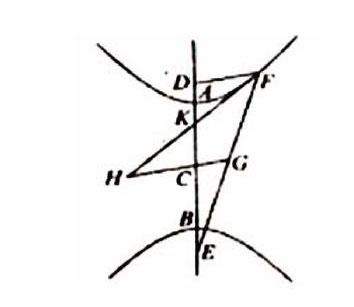
“二相對截線”的軸為AB，中心為C，且矩形AD·DB和矩形AE·EB都等于圖形的四分之一，以貼合點E和D到截線上任一點F的連線為EF和FD。且∠KFD=∠GFH。

證明：如圖所示，設過F作切線FKH，過C作GCH平行于FD，所以∠KHG=∠KFD;又因為∠KFD=∠GFH，所以GF=GH;因為C為軸AB的中心，所以AC=CB、EC=CD;因為GF=GH、AE=BD，所以GH=EG，所以FE=2GH。又因為已證CH=CB，所以EF=2（GC+CB）;因為FD=2GC，且AB=2CB，所以FE=FD+AB，即FE-FD=AB。

設計意圖：教師與學生一起證明得到雙曲線上以貼合點E和D到截線上任一點F的連線EF和FD的差是一個定值AB。此證明結果與橢圓定義對比發現都是平面內到定點距離與定長關系的曲線，這也是曲線的本質。學生在橢圓的基礎上體驗追溯雙曲線的定義，在后續的拋物線就順利追溯出相關定義。

3.概念本質，符號定義。問題（4）：能不能用數學式子表示得到的結論？

師生活動：師生通過類比歸納證明過程與結論共同得到雙曲線的定義：把平面內兩個定點的距離的差的絕對值等于非零常數（小于F1F2）的點的軌跡方程叫作雙曲線。兩個定點叫作雙曲線的焦點（阿波羅尼奧斯沒有給出“焦點”的定義，而把焦點說成是“由貼合產生的”，把它叫作“貼合點”）用數學符號表示：||PF1|-|PF2||=2a（2a

設計意圖：教師向學生重構知識的發生，學生體驗到數學在發展的過程中數學家經過火熱的思考，促進學生對知識的理解。讓學生用符號表征概念，有利于樹立學生的符號意識，發展數學觀念。

（三）雙曲線的標準方程

問題（5）：能不能類比橢圓方程推理過程，推理得到雙曲線的方程？

師生活動：教師引導學生類似推導橢圓方程一樣，建立直角坐標系，并用借助余弦定理和勾股定理探究雙曲線標準方程推導。學生合作求出雙曲線標準方程后引導學生思考焦點如果在y軸上，得到的雙曲線標準方程是？

設計意圖：學生經歷分析、歸納、推理和類比的探究雙曲線方程過程，提升數學核心素養。

（四）鞏固練習，加深概念認識

選擇一些辨別雙曲線定義和求滿足某些條件的標準方程（列出具體題目略）

設計意圖：利用練習讓學生領略數學的美學價值，有利學生理解數學概念的形成過程，提高教學效果完成教學目標，而且能提升學生對數學文化的認同感，彰顯數學的育人價值。

四、結語

教師利用數學史融入雙曲線教學，通過探究驗證過程讓學生明白知識的產生與來源，并在探究過程與歷史人物的思想產生思維的碰撞，學生可以穿過時間的洪流與歷史人物有思維的共鳴。并且在這思維碰撞中培養了學生對數學概念、定理法則的追溯能力與習慣。進而有利于學生理解數學概念的形成過程，能提升學生對數學文化的認同感，彰顯了數學的育人價值。

參考文獻

[1]中華人民共和國教育部制定.普通高中數學課程標準2017年版[M].北京：人民教育出版社，2018.

[2]Apollonius of Perga，圓錐曲線論（朱恩寬，等，譯）[M].西安：陜西科學技術出版社，2007：230-232.

[3]侯代忠，喻平.彰顯數學文化：教學設計中的三個自問[J].數學通報，2018，57（9）：32-36.

Teaching Design of Hyperbola and its Standard Equation from the Perspective of Mathematical History

LU Wen-ting， WEI Hong

（College of Mathematics and Statistics， Nanning Normal University， Nanning， Guangxi 530299， China）

Abstract： From the perspective of the history of mathematics， we can reveal the occurrence and development process of mathematical concepts， mathematical thoughts and mathematical problems. By integrating the history of mathematics into mathematics teaching and showing the origin and history of concepts to students clearly， it can not only promote students' deep understanding of mathematical concepts， but also effectively combine mathematical culture with teaching activities.

Key words： history of mathematics; hyperbola; hyperbolic equation; mathematical culture