淺談常微分方程在數學模型中的應用及其數值模擬

史詩潔 呂羽 張紅梅

[摘 要]常微分方程是重要的數學理論，在實際中具有廣泛的應用，也是數學建模的重要理論之一。基于培養“應用型”“創新型”人才的實際需求，結合實際問題—人口預測問題，分析在數學理論的課堂教學中，如何將理論知識應用于實際問題中，使學生了解數學理論的實際應用，加深學生的理解與記憶;以及在數學建模課堂的教學中，如何選擇恰當的教學內容，使學生快速掌握建模方法。

[關鍵詞]數學模型;常微分方程;分離變量法;人口模型;數值模擬

[基金項目]2018年度深圳技術大學教改研究項目“數學建模課程建設的探索”（2018.11：2018105101035）;2018年度深圳技術大學教改研究項目“新工科背景下基于LEGO Mindstorms機器人系統的大學計算機基礎課程創新教學的研究”（2018.11：2018105101031）;2020年度深圳技術大學教改研究項目“面向應用型人才的啟發與實踐有機結合的數學教學新模式探究”（2020.01：202018666601012）

[作者簡介]史詩潔（1990—），女，廣東汕頭人，博士，深圳技術大學大數據與互聯網學院講師，主要從事趨化系統解的性態研究;呂 羽（1983—），男，廣東深圳人，博士，深圳技術大學大數據與互聯網學院副研究員，主要從事機器學習算法研究;張紅梅（1973—），女，黑龍江齊齊哈爾人，博士，深圳技術大學大數據與互聯網學院副教授，主要從事數學基礎學科和應用學科的教學和研究工作。

[中圖分類號] G642;O13-4 [文獻標識碼] A [文章編號] 1674-9324（2020）45-0-02 [收稿日期] 2020-05-19

一、引言

數學是科技發展的重要理論基礎，在高等教育中占有重要的地位。其中，常微分方程是大部分理工專業的必修課程。客觀世界是實時變化的，常微分方程正是描述這種變化規律的主要工具。在高等教育中，使學生掌握理論知識只是最基本的要求，而理論的實際應用才是最終目的。本文以常微分方程[1]中最基本的類型—可分離變量方程為例，結合人口模型，說明如何將常微分方程理論應用于實際問題。對于大學理工科一年級的學生，該模型所需的預備知識以及求解方法是他們在高等數學的課堂中剛剛結束學習以及正在學習的內容，印象深刻，比較容易理解和掌握，因此學生的注意力將完全集中到整個建模的流程上，快速理解數學建模的目的，以及所學的數學理論在數學建模和實際問題中的應用價值。

二、常微分方程基礎理論

若一階微分方程F（x，y，y）=0可寫f （x）dx=g（y）dy，則稱為可分離變量方程。可分離變量方程的名稱中隱含其求解方法：

首先，對方程進行變量分離，即將兩個變量x和y分別歸攏到等式兩側，得

其次，對（1）式等號兩側同時積分，得到

若等號兩側的積分都存在，則（1）有隱式通解F（x）=G（y）+C，其中C是積分常數。

三、微分方程在數學建模中的應用

常微分方程的應用領域非常廣泛，無論在基礎科學、應用科學和社會科學中都可以找到常微分方程的影子，例如：電磁學，流體力學，海洋動力學，控制科學等。本文以社會科學中的人口預測問題為例，說明其應用。

1798年，英國人口學家馬爾薩斯提出了馬爾薩斯（Malthus）人口模型[2，3]

其中x（t）表示t時刻人口，r表示人口增長率。顯然上式是可分離變量方程，可以解得

x（t）dx=x（0）ert

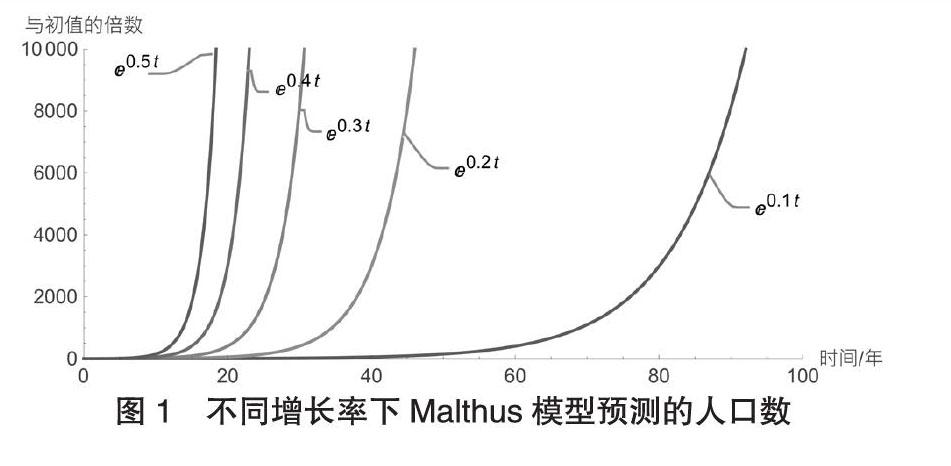
上式表明，自然增長率r一旦取定，按馬爾薩斯模型預測的人口數將以指數形式增長，如圖1所示，這顯然與實際情況是相悖的。這是源于馬爾薩斯認為生產資料對人口增長的限制是“彈性”的，因此人口增長率基本維持在一個穩定水平[3]。然而，人口增長數不僅受限于資源，還受環境承載力的影響，包括國家政策，地理環境，經濟發展水平，生態環境等。

其中，M為最大人口容量，為人口增長率。這同樣是一個可分離變量方程，其解為

基于Malthus模型與Logistic模型對1949—2020年全國人口數的預測以及實際人口數[6]，本文運用數學軟件進行數值模擬，如圖2所示。可以看出，Logistic模型自始至終可以準確預測實際的人口數量，而Malthus模型在1980年以后逐漸偏離實際的人口數，而且趨勢是無限上升，與實際情況相悖。在實際的課堂教學中，通過這個例子讓學生明白要解決實際問題，需要考慮實際情況中的影響因素，建立實用的數學模型。

雖然從圖2中還可以看到，至目前為止（2020年），Logistic模型可以準確預測實際的人口數量，但是隨著社會的進步，人們對人口數量發展規律的認識不斷加深，人口發展問題還應考慮其他因素的影響，例如生育率、性別比例、社會年齡結構、環境承載力、生活必需品等。考慮到上述因素的影響，Logistic模型中還存在哪些不足？在課程結束時，可以引導學生去發現問題，并通過改進模型來解決問題。這也是我們開設數學模型課程的初衷。

參考文獻

[1]同濟大學數學系.高等數學[M].第7版.北京：高等教育出版社， 2014：303.

[2]姜啟源.數學建模[M].第5版.北京：高等教育出版社，2005：141.

[3] [英]馬爾薩斯.人口原理[M].朱泱，等，譯.北京：商務印書館， 1992：1.

[4]王學保，蔡果蘭.Logistic模型的參數估計及人口預測[J].北京工商大學學報（自然科學版），2009（27）：75-78.

[5]顧樵.數學物理方程[M].北京：科學出版社，2015：2.

[6]國家統計局[DB/OL].http：//data.stats.gov.cn/index.htm.

The Application of Ordinary Differential Equation and Its Numerical Simulation in Mathematical Model：

Taking Population Model as an Example

SHI Shi-jie， L? Yu， ZHANG Hong-mei

（College of Big Data and Internet， Shenzhen Technology University， Shenzhen， Guangdong 518118， China）

Abstract： Ordinary differential equation is an important field in mathematics， which is widely used in practice， and is also one of the important theories of mathematical modeling. Based on the needs of applied universities to cultivate "applied" and "innovative" talents， this paper introduces a method about applying theoretical knowledge to practical problems in mathematical classes， which helps students to understand the practical application of mathematical theory， and deepens their understanding and memory. Moreover， this paper also introduces how to choose the appropriate content to make students master the modeling method quickly in the mathematical modeling class. For more details， the authors choose the population model as an application example mainly because the modeling principle of the model is simple and the method is intuitive.

Key words： mathematical modeling; ordinary differential equation; separation of variables; population model; numerical simulation