基于譜優化社區劃分的雙信源溯源算法

廖 藝，王友國，朱 亮

(1.南京郵電大學 理學院，江蘇 南京 210046；2.南京郵電大學 通信與信息工程學院，江蘇 南京 210003)

0 引 言

隨著信息技術的不斷發展，人類社會已經全面步入在線社交網絡時代。社交網絡為人與人之間的信息交流提供了絕佳渠道，并成為生活中不可缺少的一部分。社交網絡的產生使用戶具有雙重角色，既是信息的“消費者”，更是信息的“生產者”。在社交網絡大環境影響下，信息的來源、傳播速度、傳播范圍以及影響力都大幅增加[1-2]。對社交網絡上信息擴散過程的研究、分析及控制已然成為復雜網絡領域的研究熱點之一[3-4]。但是，社交網絡的飛速發展也是一把雙刃劍。謠言在社交網絡上的肆意傳播，會給社會帶來嚴重的危害，造成社會恐慌，影響社會穩定。如何快速及時有效地遏制網絡上謠言的肆意傳播顯得尤為重要[5]。

謠言溯源便是最為直接有效的方式之一。謠言溯源問題最終目的是通過信息溯源，從根源上及時有效地遏制謠言的傳播，防止其造成社會不良影響。謠言溯源是在獲得某些信息的前提下，如節點狀態、網絡拓撲信息、潛在的傳播機制等，構造源節點估計量，最大化謠言源檢測概率[6]。但是，這類問題的精確解已被證明是N-P難題。除此之外，網絡拓撲結構的復雜性、傳播過程的動態性、計算的可行性都給謠言溯源問題帶來了巨大的挑戰[7]。

針對單信源溯源問題，Shah和Zaman[8]在謠言傳播服從正則樹上的SI模型時，提出了謠言中心性，基于可能的傳播路徑數構造出極大似然估計量，并證明在一般樹圖下正確檢測概率大于零，在幾何樹圖中且傳播時間t→∞時，算法準確率趨于1；Zhu等人[9]提出Jordan中心，即距離所有感染節點距離最大值是最小的節點，用于解決SIR模型下單信源溯源問題。實驗證實，在樹型網絡下，Jordan感染中心與真實源節點的距離以高概率小于一個常數；Comin等人[10]對比感染圖與原始網絡，在中介中心性的基礎上，去除節點度的偏差，提出了無偏中介中心性，實驗表明在雪崩傳播模型下，無偏中介中心性表現最好。

針對多信源溯源問題，Fioriti等人[11]根據謠言源是加入感染網絡時間最早的節點提出動態年齡算法(DA算法)，該算法通過計算去除每個節點后，網絡鄰接矩陣最大特征值的下降量，下降量與該節點年齡成正比，經過真實網絡的模擬實驗，DA算法表現優異；Luo等人[12]借鑒Shah等人的思路，提出MSEP(multiple sources estimation and partitioning)算法，用于識別網絡中的感染源和感染區域，此外，Luo[13]對于SI模型中節點的顯式狀態和隱式狀態的多源問題，提出了多Jordan中心(multiple Jordan center estimation，MJC)算法對其求解；Zang等人[14]將無偏中介中心性推廣到只包含部分節點快照的SIR傳播模型的多源問題，提出了AUB(advanced unbiased betweenness)算法，該算法通過模塊度將多源問題轉化為多個單源問題，并以無偏中介中心性尋找謠言源。

該文在已有研究的基礎上，考慮基于譜優化的模塊度社區劃分算法，將雙信源感染子圖劃分為兩個社區，并在各個社區內進行基于謠言中心的單信源估計，最后在不同網絡拓撲結構上進行仿真與分析，同時與基于接近中心性、距離中心性和Jordan中心的啟發式估計器進行對比。

1 基于譜優化的社區劃分算法

1.1 模塊度

在真實的社交網絡中，普遍存在著一個共同的性質：同組的組內節點間相似性較大，異組的節點相似性較小，即社區結構[15]。2004年，Newman[16]提出了模塊度(modularity)的概念，用來度量網絡中社區劃分精度和優劣。這種效益函數等價于社區內的實際邊數與其期望數之差，模塊度越大表示越強的社區結構，即社區劃分算法效果越好。由于存在太多的劃分，各種近似優化算法被證明是有效的[17-18]。如圖1所示，通過感染快照和網絡結構，對雙信源感染圖進行社區劃分。

圖1 雙信源社區劃分示意圖

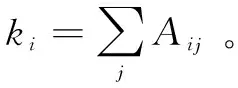
(1)

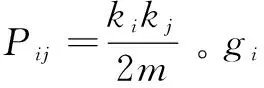
1.2 基于譜優化的模塊度矩陣

Newman[19]對模塊度做了進一步研究，結合譜分析法來優化社區劃分算法。譜分析法[20]是利用拉普拉斯矩陣的特征向量將連接緊密的節點劃分到一個社區，實對稱矩陣的非退化特征值所對應的特征向量總是正交的，所以非零特征值對應的特征向量中總是包含正負兩種元素，正負元素所對相應的節點可劃分到不同的社區。對比傳統社區劃分算法，譜分析法不易陷入局部最優解，當網絡被劃分成兩個社區時，社區劃分效果好，運算速度快[21]。

定義1：s是一個含有n個元素的索引向量，則有

(2)

通過索引向量s，將模塊度Q改寫為矩陣形式：

(3)

Bij=Aij-Pij

(4)

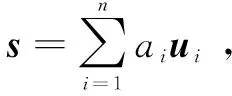
(5)

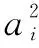
(6)

綜上所述，得到基于譜分析的模塊度社區劃分算法：通過計算模塊度矩陣B主特征向量來獲得最優s，根據元素s的正負得到劃分的兩個社區。

2 謠言溯源

2.1 謠言傳播模型

在SI模型中，每個節點可能處于兩種狀態之一：易感染(S)和已感染(I)。在任意時刻，一旦一個節點被感染，則在整個傳播過程中一直維持已感染狀態且具備傳染能力，周圍有聯系的鄰居節點將會處于易感染狀態，而每個易感染節點在下一時刻會被概率性感染。

2.2 源估計量和謠言中心

假設在無向網絡G=(V,E)中初始謠言源v*∈V，在某個時間點觀察到N個被感染節點的感染子圖，記為GN。假設源節點在感染子圖GN的所有節點之間具有統一的先驗概率。根據感染子圖GN和網絡拓撲結構，為了使正確檢測概率最大化，得到如下的極大似然估計量。

(7)

其中，PG(GN|v)是以v為謠言源觀測到感染子圖為GN的概率。

在正則樹中，節點v是謠言源的概率與該節點所有可能的傳播路徑數成正比，那么，

(8)

其中，R(v,GN)表示在傳播過程中感染圖GN中所有節點的所有可能被感染順序的計數，即謠言中心性(rumor centrality)。網絡的謠言中心是具有最大謠言中心性的節點。

在正則樹上，網絡的謠言中心是謠言源的極大似然估計，即使在一般樹上，謠言中心與極大似然估計量沒有顯著差別[8]。因此，在樹形網絡中，節點v的謠言中心性表達式為：

(9)

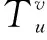
(10)

其中，TBFS(v)是GN中以節點v為根節點按照寬度優先搜索的排列。

2.3 基于譜優化社區劃分的雙信源溯源算法

算法的整體流程如圖2所示。

3 仿真與分析

通過分析不同估計量在不同網絡拓撲結構下的正確檢測概率和平均錯誤距離來評估該算法的檢測性能和優劣。正確檢測概率表示實驗中正確識別謠言源的比例，平均誤差距離表示估計謠言源與實際謠言源之間的平均距離。在仿真實驗之前，對所需估計量和定義進行相應的描述。

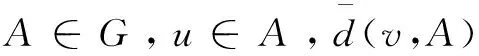
(1)接近中心性(closeness center，cc)。

(11)

(2)距離中心性(distance center，dc)。

(12)

(3)Jordan中心(Jordan center，jc)。

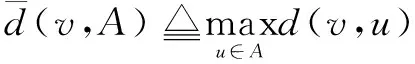
(13)

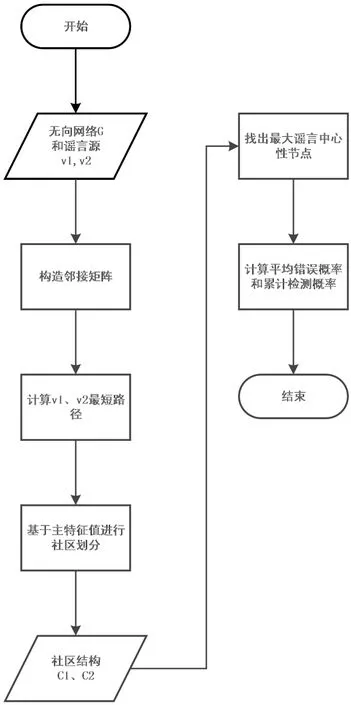
圖2 基于譜分析社區劃分的雙信源溯源算法流程

為減小隨機誤差，對所有的仿真實驗進行10 000次的蒙特卡洛模擬。具體而言，在網絡規模為1 000、平均節點度為3的規則樹，平均節點度[1,10]的隨機樹，平均節點度為12的BA無標度網絡[22]以及網絡規模為400、平均節點度為6的小世界網絡[23]上，通過以下三種常見中心度估計量作為基準與文中的估計量進行比較分析，仿真結果如圖3和圖4所示。

結合圖3和圖4可知，在樹狀網絡中，即圖3(a)(b)，基于距離中心性的溯源算法檢測性能最差，平均距離最大，在各個距離所對應的累計檢測概率均小于其余三種算法，其他三種溯源算法檢測性能相差不大。距離中心性、Jordan中心性和謠言中心性在平均錯誤距離2.5跳內，累計檢測概率均達到90%以上，其中接近中心性在規則樹中的檢測性能略強，謠言中心性在隨機樹中表現略好；由圖3(c)可知，在無標度網絡中，四種算法性能相差不大；小世界網絡為最接近真實網絡的人工網絡，由圖3(d)可以發現溯源檢測性能由大到小排列為謠言中心性>接近中心性>距離中心性>Jordan中心性，基于謠言中心性的溯源算法在錯誤距離為3跳內，累積檢測概率可達82%。因此，文中所提算法在不同網絡結構均表現優異，平均錯誤距離在2.5以下。

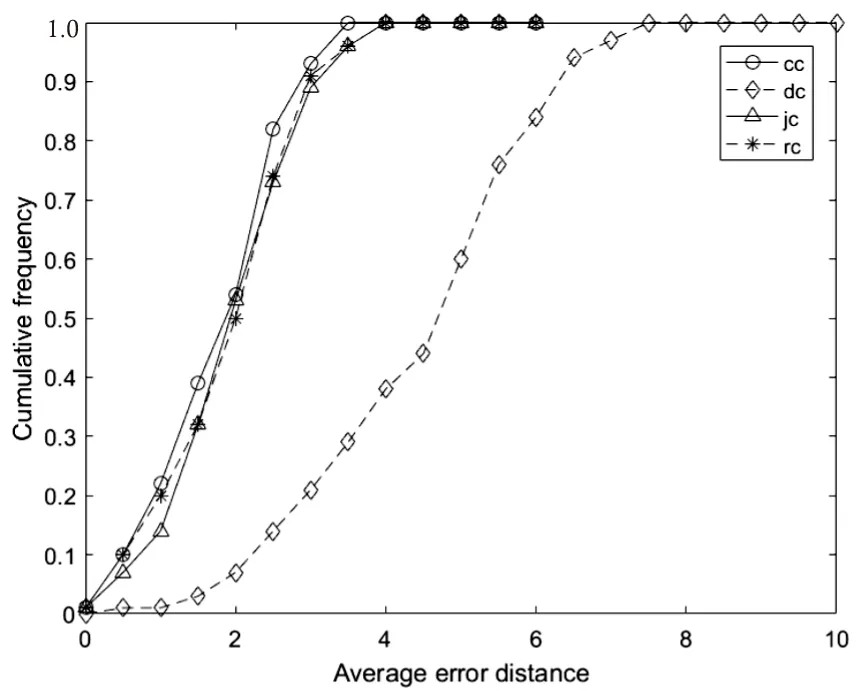
(a)規則樹

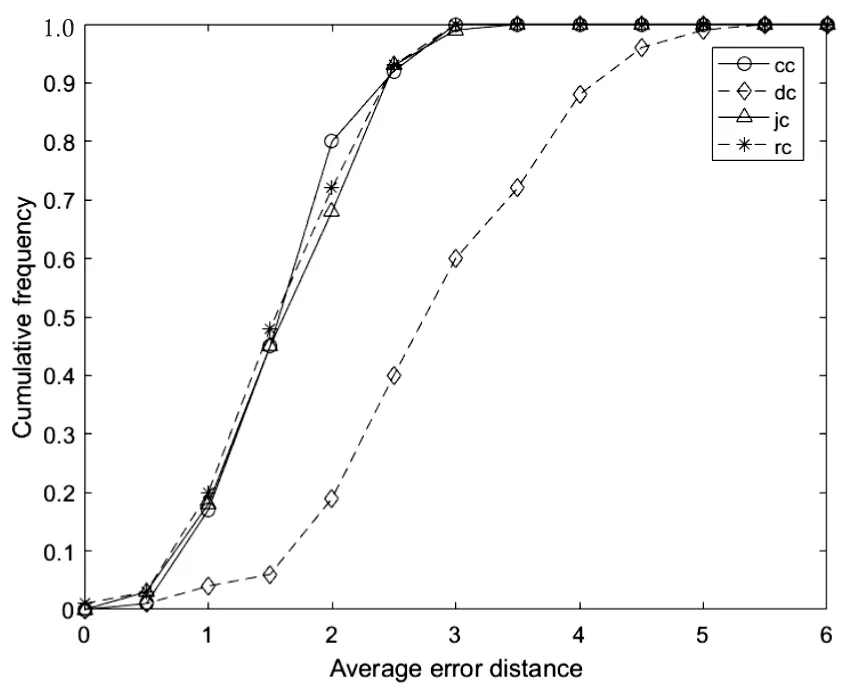
(b)一般樹

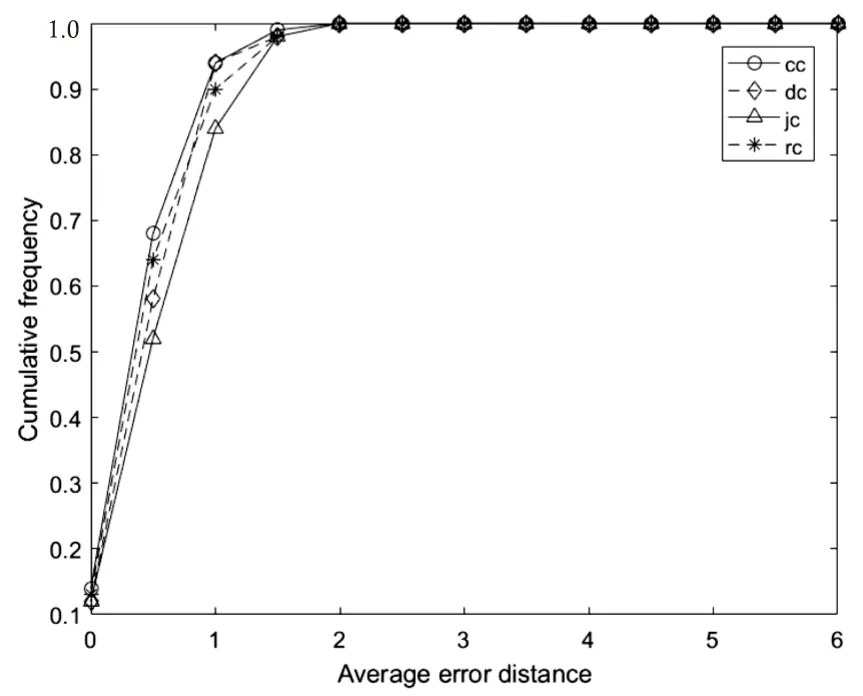
(c)BA無標度網絡

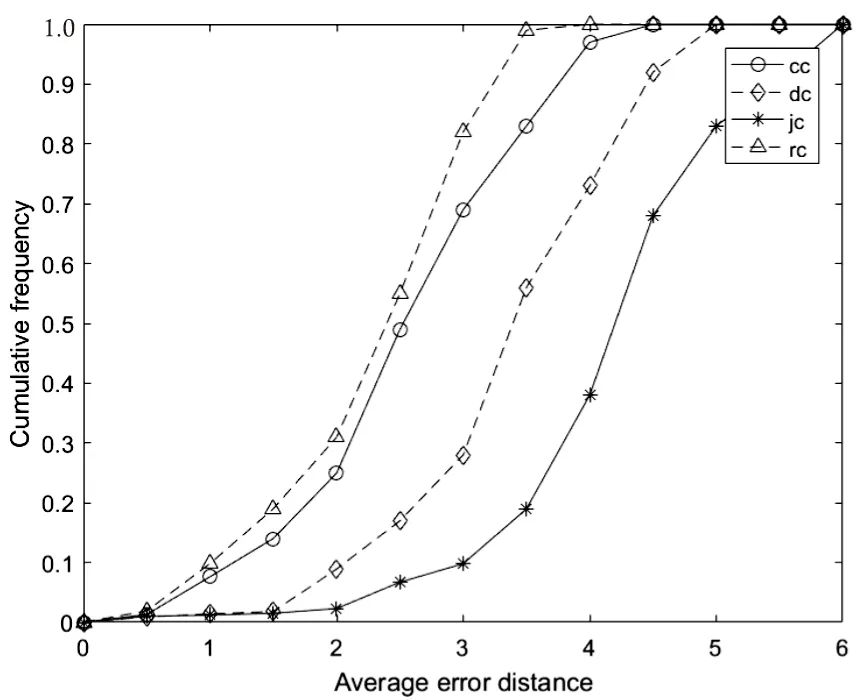
(d)WS小世界網絡

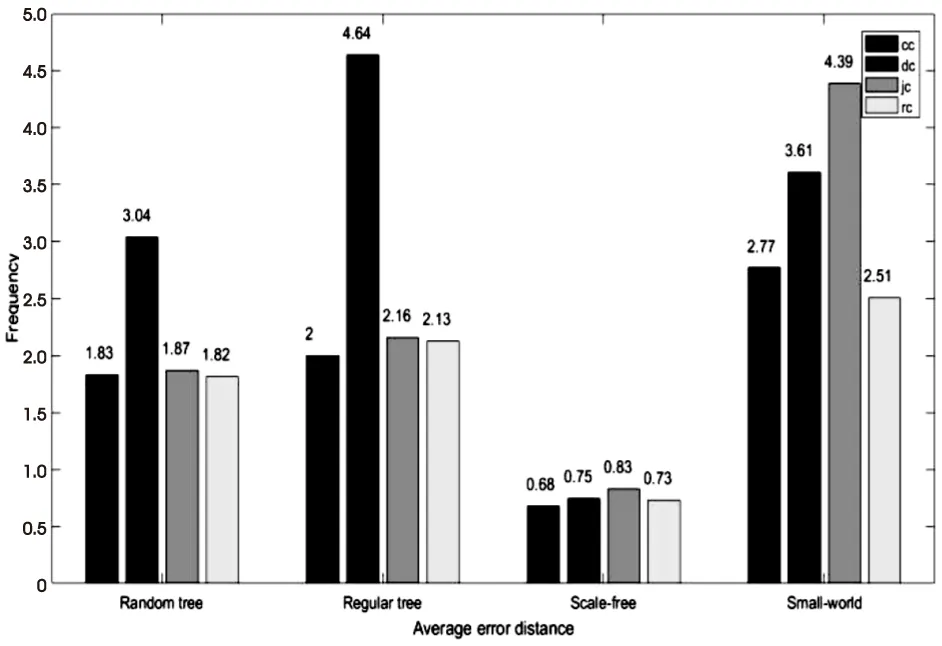
圖4 在不同網絡結構下不同估計量的平均錯誤距離對比

圖5展示的是規則樹在不同節點度和不同網絡規模下累計檢測概率隨平均錯誤距離變化曲線。仿真結果表明，隨著網絡節點度的增大，檢測性能越強，平均錯誤距離越小。同時，由于網絡規模的增大，減小了感染子圖的邊界效應，因此，檢測性能增強，平均錯誤距離減小。如圖5(a)所示，在平均錯誤距離2跳內，四種情況的累計檢測概率在50%以上，尤其在平均度為10的規則樹網絡中，累計檢測概率接近1。由圖5(b)可知，在平均錯誤距離3跳內，累計檢測概率可達85%以上。

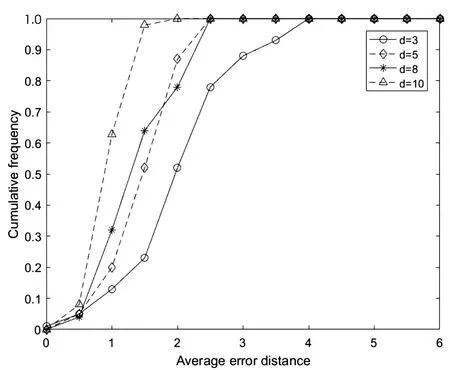
(a)不同節點度

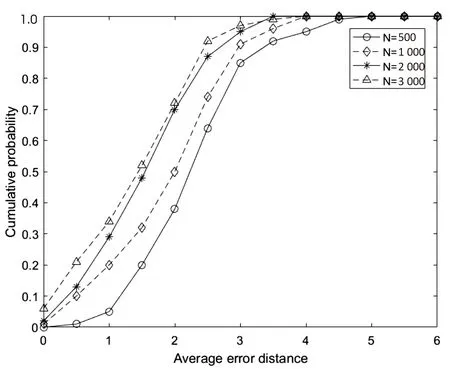
(b)不同網絡規模

綜上所述，從不同角度對文中所提算法進行仿真分析，證實了該算法檢測準確率較高，平均錯誤距離較小，溯源性能優異。

4 結束語

從復雜網絡的拓撲結構出發，基于譜優化的社區劃分算法，通過模塊化矩陣主特征向量，將雙信源感染子圖劃分成兩個社區，在各個社區內進行基于謠言中心性的單信源估計，從而將復雜的雙信源溯源分解為兩個單信源溯源問題，最后在不同人工網絡上進行了大量的仿真實驗。實驗結果表明，該算法綜合性能良好，平均錯誤距離小于2.5，累計檢測概率在55%以上，特別是在樹狀網絡和無標度網絡中該概率在90%以上。算法的時間復雜度O(N2)相比傳統的雙信源估計量低，如MSEP算法[12]的時間復雜度為O(N2d2)，MJC算法[13]的時間復雜度為O(MaxIter·|V||E|)，有效提高了計算效率。