基于改進型蜻蜓算法的車輛路徑問題研究

陶文瀚，趙晨聰，孫翌博，劉晨磊，孫知信，孫 哲

(1．南京郵電大學 現代郵政學院&現代郵政研究院，江蘇 南京 210003；2.常州工學院 計算機信息工程學院，江蘇 常州 213032；3.南京郵電大學 寬帶無線通信與傳感網技術教育部重點實驗室，江蘇 南京 210003)

0 引 言

車輛路徑問題(vehicle routing problem，VRP)[1]是物流配送優化環節中至關重要的一環。在物流配送過程中，通過為配送車輛選擇最優的運輸路徑，合理安排車輛的調度順序，可以有效減少車輛的空車行駛率和行駛距離。該問題最早由國外學者Dantzig和Ramser在1959年提出，屬于NP-Hard問題[2]。目前，國內外學者對VRP問題已經進行了廣泛而深入的研究，VRP已經應用到垃圾車的線路優化、連鎖商店的送貨線路優化等[3]眾多社會領域。

但是，傳統的VRP問題往往只考慮到配送距離而忽視了客戶對配送時間的要求,進而影響客戶對物流配送服務的滿意度。帶時間窗約束的車輛路徑問題是原車輛路徑問題的一種拓展，在經典組合優化車輛路徑問題上，引進了客戶對貨物到達時間的時間窗約束。其中，時窗約束可以分為兩種，一種是硬時間窗，要求車輛必須要在時窗內到達，早到必須等待，而遲到則拒收;另一種是軟時窗，不一定要在時窗內到達，但是超出時間窗到達則需要處罰。

該文總結眾多新型智能算法應用到車輛路徑問題上的優缺點，分析當前路徑規劃上存在的問題和需求，提出了一種改進型蜻蜓算法，并將該算法應用到帶軟時間窗約束的車輛路徑問題中，發現該算法在求解VRP問題上具有較高的可行性。

1 相關研究

目前，已有許多新型智能算法用于求解帶時間窗約束的車輛路徑問題[4]。文獻[5]通過使用禁忌搜索算法和自適應大鄰域搜索算法來解決具有時間依賴性的軟時間窗和隨機行駛時間的車輛路徑問題，并說明該方法可用于解決其他一些大規模問題。文獻[6]利用人工蜂群激發蜜蜂的覓食行為，運用混合超啟發式算法求解帶軟時間窗的多目標車輛路徑問題。文獻[7]提出了一種使用分布估計算法的方法，通過使用廣義的Mallows分布作為概率模型來描述解空間的分布，以解決帶時間窗的車輛路徑問題。文獻[8]探索了時變多行車輛路徑問題(TDMTVRP)，使用了具有改進行進速度的模型，與容量較大的VRPTW[9]相比，減少了行車時間和行進距離，并通過使用最近鄰啟發式算法獲得初始解和禁忌搜索啟發式算法搜索最優解。文獻[10]提出了一種基于改進的頭腦風暴優化算法(IBSO-ACO)的新型蟻群優化算法，以解決帶有軟時間窗的車輛路徑問題。文獻[11]開發了一種混合遺傳算法的求解方法，對遺傳算法和變量鄰域搜索方法(VNS)進行了雜交，以解決帶有軟時間窗的靜態和動態車輛路徑問題。這些學者對帶有時間窗的車輛路徑問題進行了系統而深入的研究，但他們的研究大多使用改進型的傳統啟發式算法，例如遺傳算法、蟻群算法和禁忌搜索算法等。這些算法在帶時間窗約束VRP的求解上取得了可喜的成果，但也存在不少問題，如禁忌搜索算法對初始解的依賴性較高，遺傳算法存在局部搜索能力不強、易陷入早熟、總體上可行解的質量不是很高等缺點。

蜻蜓算法(dragonfly algorithm，DA)自從2015年被Mirjalili[12]提出就得到了廣泛的研究與應用。該新型算法已被成功用于醫療疾病預測診斷[13]、太陽能熱系統優化[14]、小麥碰撞聲信號檢測與識別[15]等諸多領域。其中，Abdelaziz I. Hammouri等[16]將蜻蜓算法運用到旅行商問題(TSP)的求解之中，驗證了蜻蜓算法在求解類路徑規劃問題的可行性。文獻[17]使用DA來估計隨機部署在指定區域中的節點的位置，通過仿真實驗來表明DA可以為基于范圍的定位產生低誤差。文獻[18]提出了一種用于預測問題的帶有極限學習機(ELM)系統的混合蜻蜓算法，通過利用DA在隱藏層中選擇較少數量的節點，以加快ELM的性能。

然而，在軟時間窗的約束下，針對原蜻蜓算法解決大規模問題時存在收斂速度慢、運算時間長、容易陷入局部最優解等缺陷[19]，該文提出一種改進型的蜻蜓算法應用于車輛路徑問題，從而更好地提高物流運輸車輛的配送效率。

2 問題描述及數學模型

帶時間窗約束的車輛路徑問題可以描述為：一個配送中心，擁有一定數量的同種車輛，車輛容量有限且已知，車輛滿載貨物由配送中心出發，向區域內若干客戶配送同種商品，要求在完成配送任務的總路程最短的基礎上派出的車輛數最少，并考慮在客戶點的駐留成本、未在規定時間內送達的懲罰成本。

該文從實際物流車輛運輸特點和自身實驗條件出發，對構建的帶時間窗約束的車輛路徑問題數學模型進行如下假設：

(1)車輛必須從固定的配送站點出發，運輸途中不經停該站點，在完成一趟運輸過程之后才能回到配送站點；

(2)規定車輛以一種恒定的行駛速度在各站點之間行駛；

(3)各服務點的需求量、服務時間窗、服務時間不會臨時變動；

(4)各服務點之間的路徑都可達，并且不會產生任何突發事件影響車輛的行駛；

(5)一輛車只可以同時服務一個服務點、配送一條路線。

根據以上數學模型假設，對構建的帶時間窗的車輛路徑問題數學模型中的參數和相關的變量進行如下定義：

V={1,2,…,n}表示站點編號集合，n為站點總個數，編號1為起始站點。

Pos表示配送站點和客戶服務站點的位置集合，其中(Posix,Posiy)表示站點i的橫、縱坐標位置。

Dis表示各個站點之間的距離，站點i與站點j之間的距離Disij由式(1)給出。

(1)

Ser_Time為站點的服務時間集合，其中Ser_Timei表示站點i的服務時間。

Demand為站點的服務需求量集合，其中Demandi表示站點i的貨物需求量。

TW表示各站點規定的服務時間窗，其中TWilast表

示站點i服務時間窗的最大非處罰服務時間。

duty記錄車輛已經服務過的站點序列。

v_vel表示車輛行駛的速度。

v_cap表示車輛的最大載重量。

αij判斷車輛是否經過站點i和站點j之間的路線。當αij=1時，表示車輛經過；當αij=0時，表示車輛沒有經過。

βi判斷站點i是否已經服務過。當βi=1時，表示站點i已經服務過；當βi=0時，表示沒有服務過。

γi判斷車輛在到達站點i時時間是否超出該站點的時間窗上限。當γi=1時，表示超過；當γi=0時，表示沒有。

time記錄車輛剛到達某一站點時的當前時間，其計算公式由式(2)給出。

(2)

ctrans、cser和cpun分別表示車輛單位行駛路程、單位服務時間和單位懲罰時間成本。

綜上所述，該文構建的數學模型目標函數由式(3)給出。

Ser_Timei-TWilast)*cpun

(3)

約束條件如下所示。

(4)

(5)

(6)

0≤d_n≤n

(7)

(8)

(9)

3 模型實現

3.1 蜻蜓算法概述

蜻蜓算法是受蜻蜓行為啟發而提出的一種新型群智能算法。與其他的群智能優化算法類似的是，蜻蜓算法也有著較好的局部最優解避免能力和精確近似全局最優解的能力。

蜻蜓算法像大多數群智能算法一樣皆是遵循“求生”的原則，蜻蜓個體有兩個行為：尋找食物和躲避天敵，蜻蜓群體的位置移動由以下五種行為組成：

(1)分離，即蜻蜓與相鄰個體之間避免碰撞。

式中，X是當前個體的位置；Xj是第j個附近個體的位置；N是附近個體的個數。

(2)結隊，即相鄰個體之間傾向于保持相同的速度。

式中，Vj是第j個附近個體的速度。

(3)聚集，即蜻蜓傾向于向相鄰個體中心聚集。

(4)覓食，即蜻蜓對食物的傾向度。

Fi=X+-X

式中，X+是蜻蜓食物的位置。

(5)躲避天敵，即蜻蜓避免被天敵捕食，對其產生排斥。

Ei=X-+X

式中，X-是蜻蜓天敵的位置。

除以上五種行為之外，為了較為準確地模擬出蜻蜓的移動過程，Mirjalili又引入了兩個量：步長向量(dX)和位置向量X。步長向量計算公式如下(這是逐維定義的步長)：

ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔXt

式中，s表示分離權重，a表示結隊權重，c表示聚集權重，f表示食物因子，e表示天敵因子；Si表示第i個體分離之后的位置，Ai表示第i個體結隊之后的位置，Ci表示第i個體聚集之后的位置，Fi表示第i個體蜻蜓食物的位置，Ei表示第i個體蜻蜓天敵的位置；w表示慣性權重；t表示當前迭代次數。

位置更新如下：

(6)附近存在蜻蜓個體，則按照如下方式更新：

Xt+1=Xt+ΔXt+1

(7)附近不存在蜻蜓個體，則執行萊維飛行：

Xt+1=Xt+Levy(d)×Xt

式中，d是求解問題的維數。

3.2 改進型蜻蜓算法

通過研究發現，采用傳統蜻蜓算法求解帶時間窗的車輛路徑問題時，存在收斂精度較低、最優解容易陷入局部收斂等缺陷。因此，為了針對求解帶時間窗的車輛路徑問題，該文根據以上設計的數學模型，將隨機學習優化[20]的思想融入到蜻蜓算法中，重新設計了一種能夠更有效應用于帶時間窗約束的車輛路徑問題研究的改進型蜻蜓算法。

該算法的主要改進點在于將傳統蜻蜓算法結隊、覓食、避敵、避撞、聚集五種行為的實值計算形式，修改為隨機學習目標位置對，即利用隨機學習優化方法完成以上行為的實現：

(1)通過向同期蜻蜓種群中位置最優的蜻蜓隨機學習一組排序，更新位置序列，優化局部最優解，實現結隊行為；

(2)向歷史蜻蜓種群中位置最優的蜻蜓隨機學習一組排序，優化位置序列，趨向于全局最優解，實現覓食行為；

(3)通過遠離同期蜻蜓種群中位置最差的蜻蜓位置，避免陷入局部最優，實現避敵行為；

(4)發生碰撞時，隨機長度隨機打亂一只蜻蜓位置，保證種群多樣性，實現避撞行為。

該算法的具體實現步驟如下：

步驟1：初始化蜻蜓算法和數學模型的相關參數。其中，每一只蜻蜓的位置向量表示一種選路方式，即為除編號1外的n-1個站點編號的隨機排列組合；

步驟2：計算初代各解，即站點間的距離矩陣、每只蜻蜓位置向量所對應的成本值、初代最優解和最優成本值等；

步驟3：開始迭代計數，令迭代標識符iter=1；

步驟4：通過結隊、覓食、避敵、避撞等行為，進行隨機學習優化排序，優化各蜻蜓的位置向量；

步驟5：利用目標函數計算每只蜻蜓位置向量所對應的運輸成本值，并且記錄最優值和最優蜻蜓位置向量，即記錄最佳的成本值和對應的車輛路徑規劃方案；

步驟6：將本代最優值和歷史最優值進行比較，篩選得出最優成本值和最優蜻蜓位置向量；

步驟7：迭代標識符加1；

步驟8：判斷是否達到最大的迭代次數。若是，進入步驟9；若否，返回步驟4；

步驟9：得出實驗結果，生成實驗圖表，結束。

3.3 基于改進蜻蜓算法的模型實現

基于改進型蜻蜓算法的帶時間窗約束的車輛路徑問題模型實現流程如圖1所示。

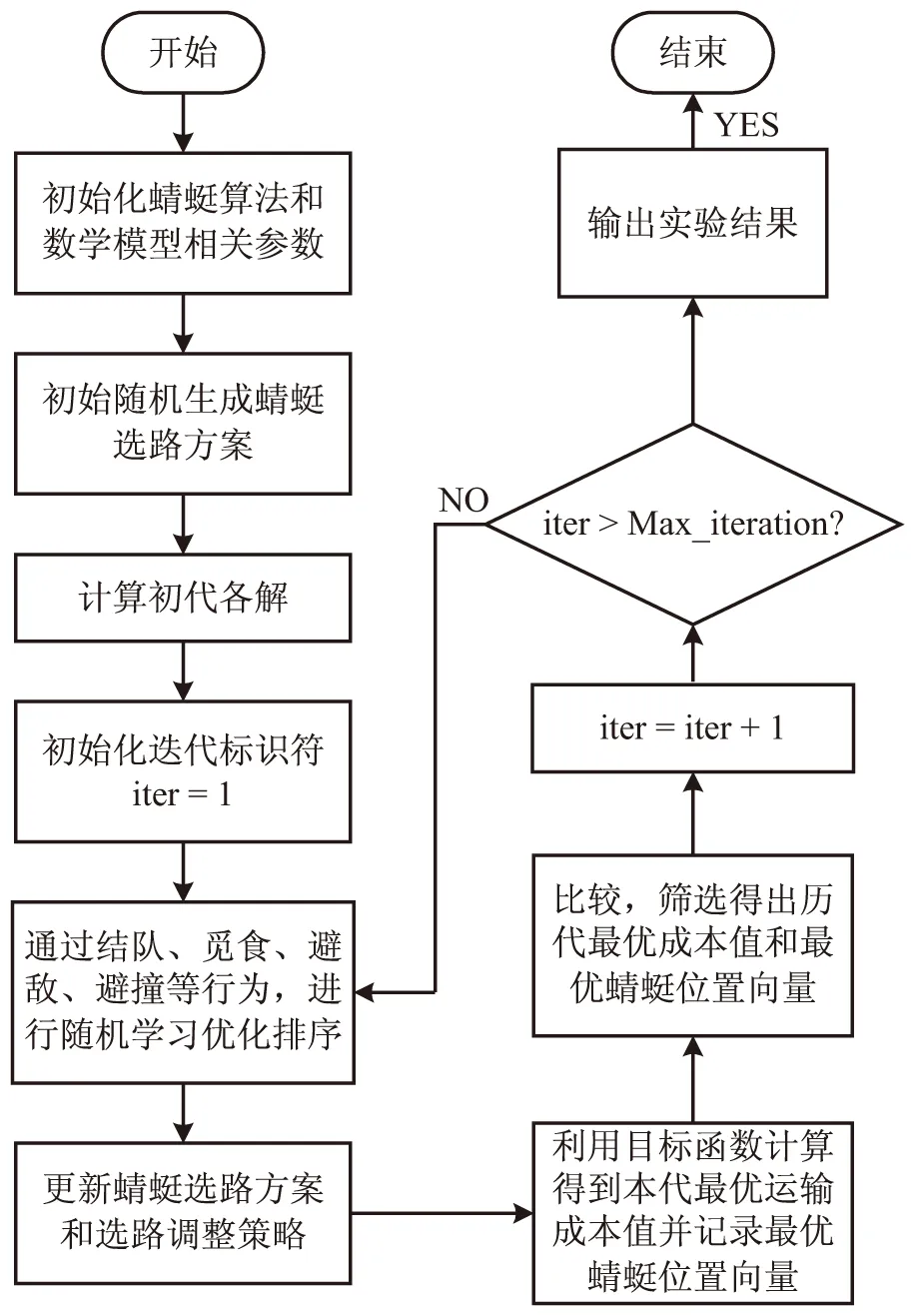
圖1 改進型蜻蜓算法實現流程

4 算例實驗

4.1 實驗參數設置

服務站點初始參數設置如表1所示。

表1 服務站點參數設置

車輛初始參數設置如表2所示。

表2 車輛參數設置

改進蜻蜓算法的初始參數設置如表3所示。

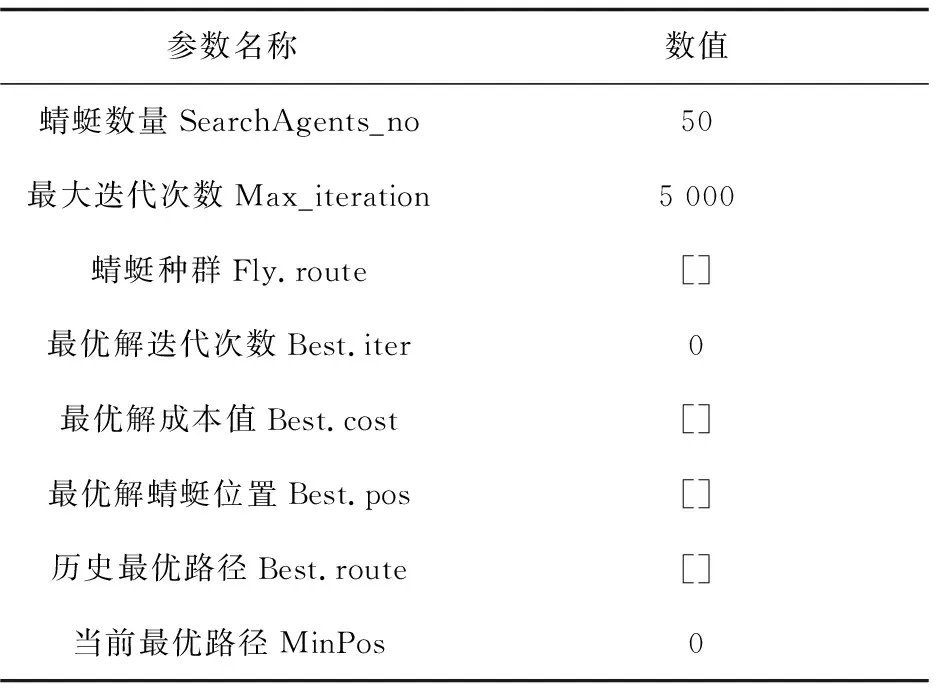
表3 蜻蜓算法參數設置

實驗設計的拓撲網絡環境如圖2所示。

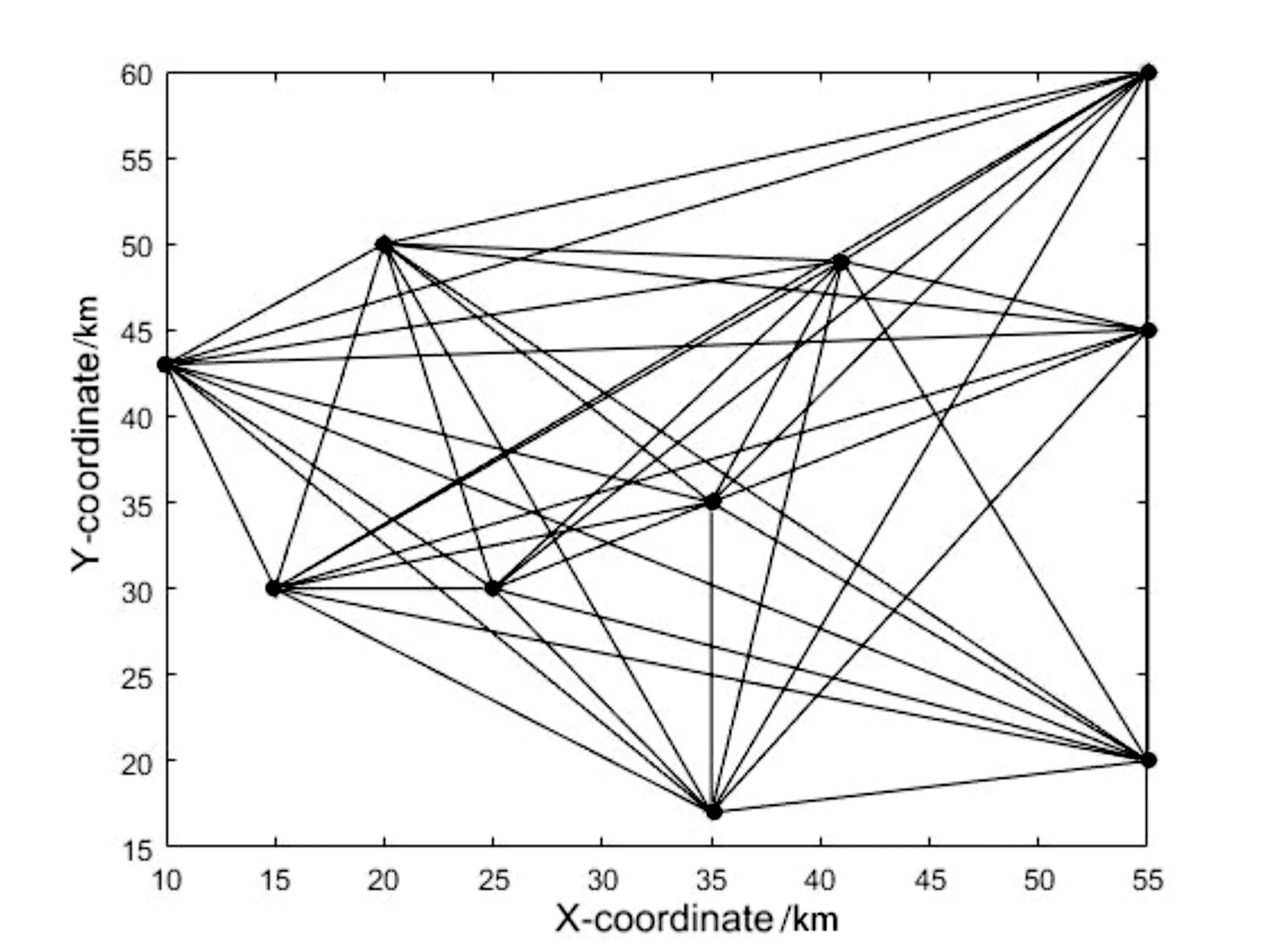
圖2 實驗物流網絡拓撲

根據該文設計的帶時間窗車輛路徑問題數學模型約束條件，該物流拓撲網絡一共擁有3 628 800種車輛路徑規劃方案。

4.2 實驗結果

針對文中的車輛路徑問題所提出的數學模型，將遺傳算法(GA)、禁忌搜索算法(TSA)、傳統蜻蜓算法(DA)和改進后的蜻蜓算法(RDA)一同進行實驗測試并進行比較。為保證實驗的公平性和客觀性，將以上四種算法的迭代次數設為1 000次，采用相同的成本函數進行運算，得到的算法對比結果如圖3所示。

由實驗結果可以看出，無論是在求解精度還是收斂速度上，改進型蜻蜓算法都展現出優越的性能，充分說明改進型蜻蜓算法在求解車輛路徑問題時具有更加穩定的性能。

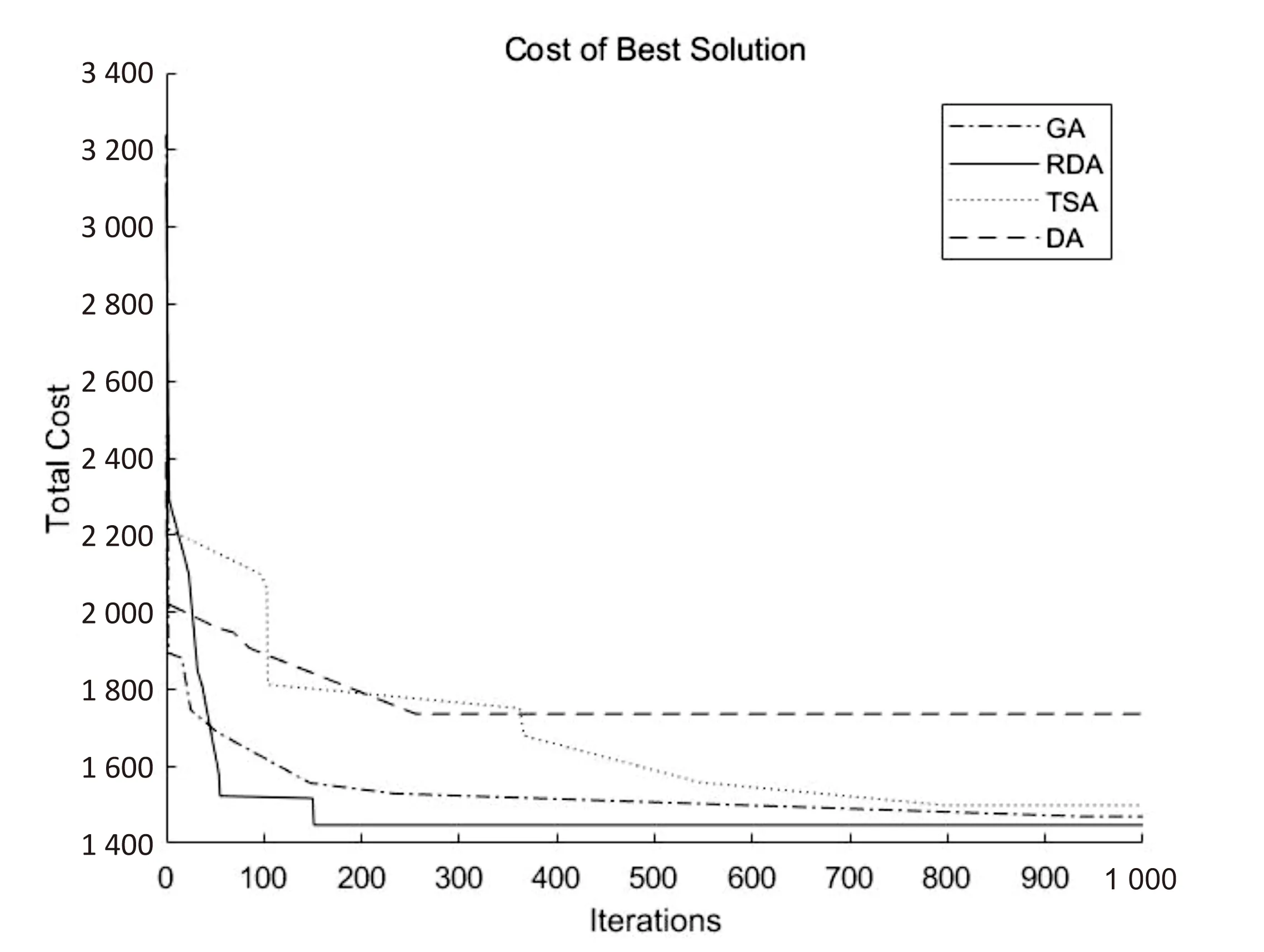
圖3 算法對比

經過實驗得到最優的綜合成本為1 447.23。其對應的車輛路徑規劃方案如圖4所示。

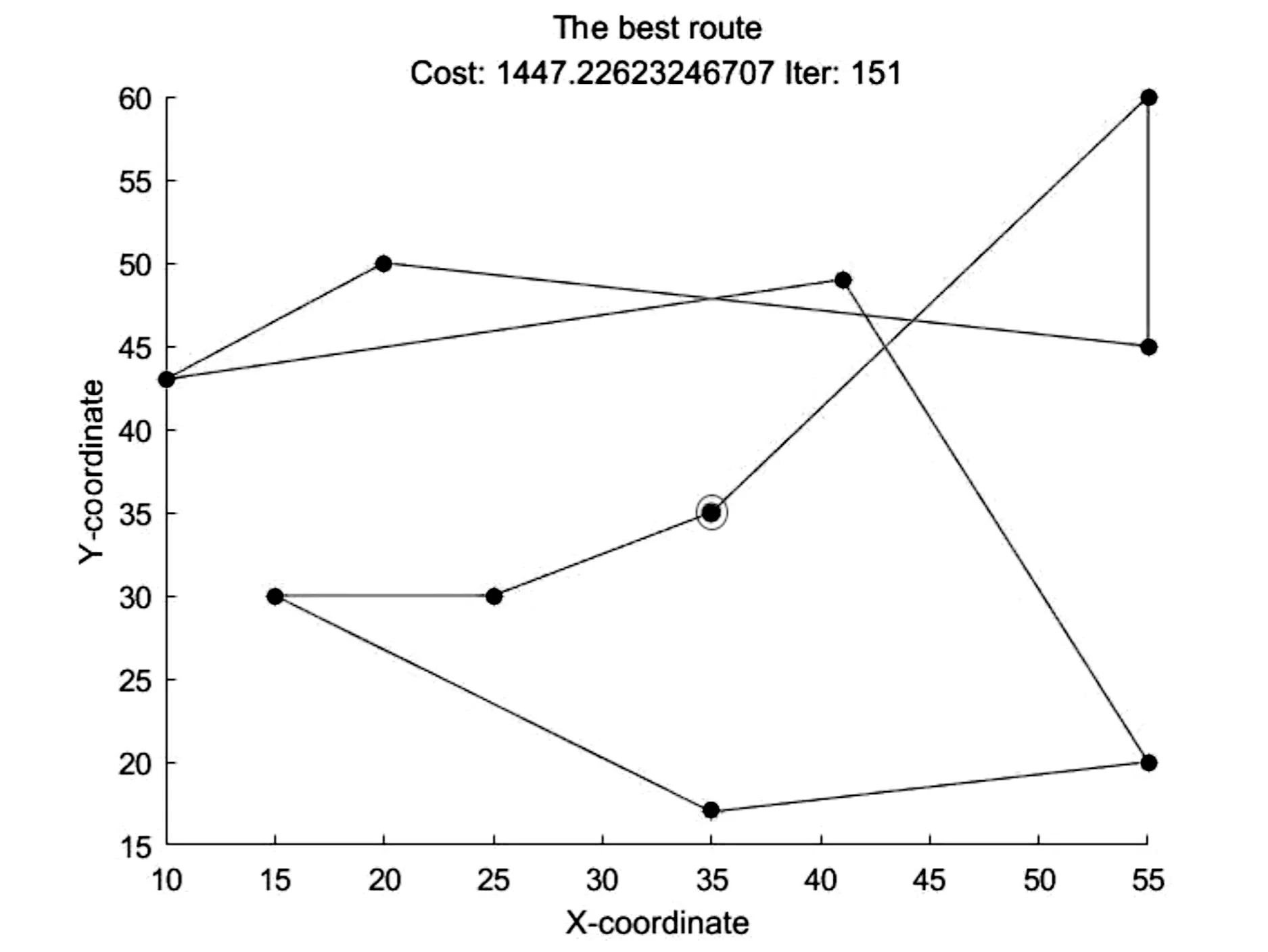
圖4 最優路線規劃

路線規劃方案為1→7→6→3→5→2→9→8→4→10。其中，加圈位置為站點1，即始發站點。

5 結束語

討論了帶軟時間窗約束的車輛路徑問題，構建了一種更符合配送中心與顧客服務目標優化的帶時間窗約束的車輛路徑問題數學模型。通過設將隨機學習優化的思想融入到原先的蜻蜓算法之中，針對車輛路徑問題數學模型的求解，重新設計了一種能夠更有效應用于該問題求解的改進型蜻蜓算法。

該算法的主要改進之處為：將傳統的蜻蜓算法結隊、覓食、避敵、避撞、聚集五種行為原則從原先的實值計算形式修改成為隨機學習目標位置對，即利用隨機學習優化方法完成以上行為的實現，使改進型蜻蜓算法更符合解的特性，從而得到一個更優的結果。

通過Matlab仿真實驗證明了將蜻蜓算法應用到帶軟時間窗約束的車輛路徑問題求解的可行性，并且驗證了改進型蜻蜓算法用于該數學模型實現的有效性。下一步將在該研究的基礎上，提高算法收斂速度和收斂精度，改進蜻蜓隨機學習的優化方式，并將該算法應用于其他領域的優化。