碰摩約束下柔性轉(zhuǎn)子模態(tài)特性及其計算方法

于平超，陳果，王存，楊默晗

1. 南京航空航天大學 民航學院，南京 211106 2. 北京動力機械研究所，北京 100074

由于航空發(fā)動機對氣動效率極高要求，其轉(zhuǎn)靜件間隙不斷減小，同時航空發(fā)動機在全壽命周期內(nèi)遭遇的載荷工況又極為復雜，導致碰摩一直是航空發(fā)動機中的常見現(xiàn)象。轉(zhuǎn)靜件碰摩會引發(fā)轉(zhuǎn)子劇烈振動以及轉(zhuǎn)子軸系內(nèi)部的交變應力，進而導致轉(zhuǎn)子軸系的疲勞斷裂，危及轉(zhuǎn)子乃至整機的安全運行，是影響航空發(fā)動機結(jié)構可靠性的關鍵問題之一。

當碰摩發(fā)生時，會對轉(zhuǎn)子產(chǎn)生沖擊、摩擦以及約束等多種物理效應[1-2]，進而帶來轉(zhuǎn)子復雜的物理現(xiàn)象，為此國內(nèi)外學者開展了廣泛的研究。Muszynska[3]對轉(zhuǎn)靜子局部碰摩問題進行了研究，表明系統(tǒng)存在階次為1/2、1/3、1/4的次諧波振動。Chu和Zhang[4]對碰摩轉(zhuǎn)子的分岔和穩(wěn)定性進行了分析，揭示了轉(zhuǎn)子動力響應從穩(wěn)定周期運動經(jīng)過倍周期分岔、擦邊分岔等變?yōu)閿M周期和混沌響應的過程。Chen等[5]針對航空發(fā)動機整機系統(tǒng)碰摩，建立了梁單元整機模型，分析了碰摩剛度比、不平衡量等參數(shù)對轉(zhuǎn)子振動響應、分岔以及混沌特性的影響。Ma等[6-8]建立了單點、多點以及全周碰摩形式的轉(zhuǎn)子模型，研究了不同碰摩形式對轉(zhuǎn)子系統(tǒng)時頻響應和軸心軌跡的影響。

碰摩除對轉(zhuǎn)子產(chǎn)生非線性激勵作用外，還對轉(zhuǎn)子產(chǎn)生約束效應。約束效應，即轉(zhuǎn)子與靜子一直接觸或者持續(xù)間斷接觸而導致轉(zhuǎn)子系統(tǒng)剛度增加的現(xiàn)象，也稱剛化效應[9]。利用該現(xiàn)象，Chu和Lu[10]建立了碰摩過程中轉(zhuǎn)子系統(tǒng)剛度的參數(shù)識別方法，并將其應用于碰摩轉(zhuǎn)子的故障診斷。Wang等[11]分析了碰摩約束對轉(zhuǎn)子動力學特性的影響，指出附加約束剛度使轉(zhuǎn)子共振區(qū)間擴張，并出現(xiàn)不穩(wěn)定接觸區(qū)域。

由于碰摩約束導致的轉(zhuǎn)子系統(tǒng)剛度變化，會使轉(zhuǎn)子系統(tǒng)模態(tài)頻率/振型改變，然而以往碰摩研究中很少關注碰摩轉(zhuǎn)子這類強非線性系統(tǒng)的模態(tài)特性。Hong等[12]結(jié)合Floquet理論和Hill方法建立了間歇碰摩轉(zhuǎn)子模態(tài)特性的計算方法，分析了碰摩約束剛度時變對轉(zhuǎn)子模態(tài)頻率和穩(wěn)定性的影響，但該方法需事先假設碰摩過程，局限性較大。陳艷華和江俊[13]首次將非線性模態(tài)理論引入到碰摩轉(zhuǎn)子中，通過解析方法推導獲得了碰摩轉(zhuǎn)子的模態(tài)頻率，其分析思路為研究碰摩約束對轉(zhuǎn)子模態(tài)的影響提供了借鑒。在此之上，Hong等[14]通過半解析的諧波平衡法建立了碰摩轉(zhuǎn)子模態(tài)的計算方法，分析了碰摩約束轉(zhuǎn)子的模態(tài)特征和穩(wěn)定性演化過程。然而，目前關于碰摩轉(zhuǎn)子模態(tài)的研究僅局限于單盤Jeffcott轉(zhuǎn)子這類簡化系統(tǒng)，對于以航空發(fā)動機轉(zhuǎn)子為代表的這類工程復雜柔性轉(zhuǎn)子，其不僅具有復雜質(zhì)量/剛度分布、陀螺效應影響，同時工作轉(zhuǎn)速范圍內(nèi)含多階彎曲模態(tài)[15]，碰摩約束對轉(zhuǎn)子模態(tài)特性的影響更加復雜。另一方面，工程中的轉(zhuǎn)子系統(tǒng)往往需要大量自由度進行描述[16]，這使得現(xiàn)有求解碰摩轉(zhuǎn)子非線性模態(tài)的解析或半解析方法無法勝任。

鑒于此，本文在非線性模態(tài)理論框架下，研究具有真實結(jié)構特征的航空發(fā)動機柔性轉(zhuǎn)子在碰摩約束下的模態(tài)特性。首先，針對柔性轉(zhuǎn)子復雜結(jié)構特征，基于梁單元有限元法建立考慮碰摩約束的轉(zhuǎn)子動力學模型；其次，結(jié)合頻域中自由度壓縮、諧波平衡思想以及時頻轉(zhuǎn)換技術等提出一套適用于含大規(guī)模自由度復雜轉(zhuǎn)子非線性模態(tài)的求解方法；最后，詳細分析碰摩約束對實際航空發(fā)動機低壓柔性轉(zhuǎn)子模態(tài)特性的影響規(guī)律。

1 考慮碰摩約束的柔性轉(zhuǎn)子動力學模型

圖1所示為典型高涵道比渦扇發(fā)動機低壓柔性轉(zhuǎn)子示意圖，轉(zhuǎn)子包含風扇、多級增壓級及渦輪葉盤，并采用0-2-1三支點支承方案。由于葉盤、錐殼等結(jié)構使用，轉(zhuǎn)子具有較為復雜的質(zhì)量/剛度分布。同時，此類轉(zhuǎn)子具有細長軸段、懸臂大質(zhì)量/轉(zhuǎn)動慣量、長跨度支承等結(jié)構特點，為典型弱剛度柔性轉(zhuǎn)子，工作轉(zhuǎn)速范圍內(nèi)通常會有多階彎曲模態(tài)被激起。當碰摩發(fā)生時，碰摩產(chǎn)生的約束剛度往往與轉(zhuǎn)子自身的橫向等效剛度相當，這將導致柔性轉(zhuǎn)子多階模態(tài)均可能發(fā)生顯著變化。

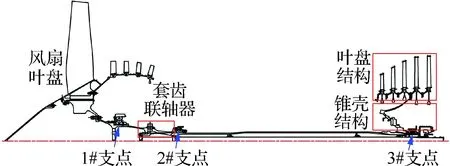
圖1 航空發(fā)動機低壓柔性轉(zhuǎn)子結(jié)構示意圖Fig.1 Schematic diagram of low-pressure flexible rotor structure in aero engines

1.1 柔性轉(zhuǎn)子的有限元建模方法

針對圖1所示的柔性轉(zhuǎn)子，建模的關鍵是準確模擬其質(zhì)量/轉(zhuǎn)動慣量、橫向剛度沿軸向的分布特征，為此采用模化能力較強的有限元法進行動力學建模。

本文基于梁單元建立此類轉(zhuǎn)子的模化方法，基本流程如下：首先基于低壓轉(zhuǎn)子的CAD模型進行結(jié)構簡化，簡化過程如圖2所示，忽略螺栓、篦齒等局部結(jié)構，采用等截面直梁模擬軸段和鼓筒，變截面梁模擬錐殼，彈簧單元模擬支承。對于葉盤結(jié)構，采用質(zhì)量單元模擬，保證質(zhì)量元的質(zhì)量和轉(zhuǎn)動慣量與實際葉盤結(jié)構的質(zhì)量和轉(zhuǎn)動慣量一致；值得說明的是，葉盤結(jié)構也可采用梁單元模擬，通過仔細劃分模擬葉盤結(jié)構的梁單元截面使得該部分梁單元的質(zhì)量和轉(zhuǎn)動慣量與實際葉盤結(jié)構一致即可。本文中，風扇葉盤采用梁單元模擬，其他葉盤結(jié)構采用質(zhì)量元，最終建立的簡化模型如圖3(a)所示。

圖2 轉(zhuǎn)子模型簡化示意圖Fig.2 Simplification process of rotor model

其次，根據(jù)上述簡化模型，在ANSYS中建立其有限元模型，梁單元采用Beam188單元，質(zhì)量單元為Mass21，彈簧單元為Combin14。梁單元截面屬性和質(zhì)量單元實常數(shù)通過上述簡化模型獲得，彈簧單元的實常數(shù)基于發(fā)動機實際支承剛度獲得。所建立的有限元模型如圖3(b)所示，模型包含46個單元和40個節(jié)點，需要說明的是，梁單元實際為一維的中心線模型，圖3(b)是ANSYS中為了視覺效果而設置的截面顯示功能。

為了保證模型的精度，一方面在進行結(jié)構簡化和網(wǎng)格劃分時，需要校核關鍵部件質(zhì)量、轉(zhuǎn)動慣量與真實值的誤差，以及軸段的等效剛度與真實值的誤差，以此為基礎進行適當修正；另一方面，對于建立好的模型，也可以通過模態(tài)分析結(jié)果與試驗模態(tài)結(jié)果或者精細的實體有限元模型模態(tài)分析結(jié)果進行對比，驗證模型的精度。本文所建立模型與所方提供的實體模型模態(tài)計算結(jié)果對比，所關心模態(tài)的誤差均在5%以下，滿足精度要求。

圖3 低壓柔性轉(zhuǎn)子的梁單元有限元模型Fig.3 Beam element model of low-pressure flexible rotors

1.2 轉(zhuǎn)靜件碰摩約束模型

圖4所示為轉(zhuǎn)子系統(tǒng)碰摩約束模型，當轉(zhuǎn)子振幅超過轉(zhuǎn)靜間隙r0時，轉(zhuǎn)子與機匣發(fā)生碰摩，假設機匣剛度為kc，轉(zhuǎn)靜件之間的摩擦系數(shù)為μ，該截面p處轉(zhuǎn)子位移為xp和yp，令zp=xp+iyp，i為復數(shù)，則碰摩對轉(zhuǎn)子產(chǎn)生的附加剛度為

k′=H(|zp|-r0)kc(1+isign(vrel)μ)·

(1-r0/|zp|)

(1)

式中：vrel=ω|zp|+Ω·rp,bd為碰摩點相對速度，ω為進動角速度，Ω為轉(zhuǎn)子旋轉(zhuǎn)角速度；rp,bd為截面p處的葉盤半徑；H(·)為Heaviside函數(shù)；sign(·)為符號函數(shù)，表達式為

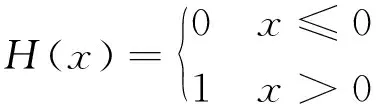
(2)

(3)

將碰摩剛度分解到x和y方向，可以獲得截面p處由碰摩產(chǎn)生的附加剛度矩陣：

(4)

可以看出，碰摩附加剛度矩陣為節(jié)點自由度xp和yp的非線性函數(shù)，且其在非對角線元素上存在非0項，即碰摩約束引起x和y向的交叉耦合。根據(jù)節(jié)點自由度編號將各截面處由碰摩產(chǎn)生的附加剛度矩陣進行組集，便可得到整體的碰摩附加剛度矩陣K′。

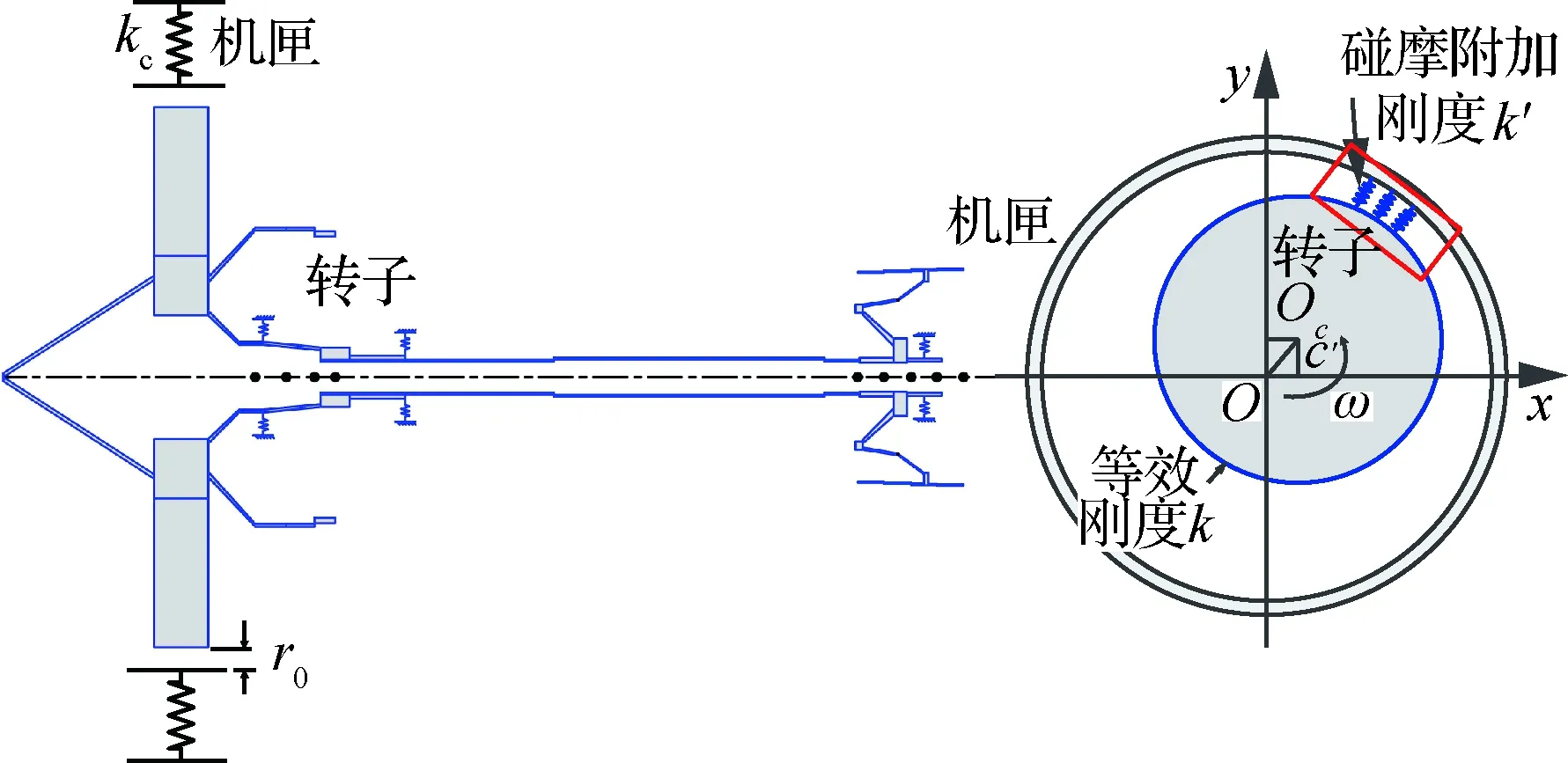
圖4 轉(zhuǎn)子系統(tǒng)的碰摩約束模型Fig.4 Rubbing constraint model of rotor system

1.3 考慮碰摩約束的轉(zhuǎn)子動力學方程

根據(jù)1.1節(jié)柔性轉(zhuǎn)子動力學建模方法，可在ANSYS獲得柔性轉(zhuǎn)子有限元模型，并將其質(zhì)量矩陣、剛度矩陣、阻尼矩陣及陀螺矩陣導出。進一步在對應自由度位置處引入1.2節(jié)的轉(zhuǎn)靜碰摩約束模型，可獲得含碰摩約束的柔性轉(zhuǎn)子動力學方程：

K′(u)u(t)=0

(5)

式中：M、C、G、K、u分別為質(zhì)量、阻尼、陀螺、剛度矩陣和位移向量；K′(u)為附加剛度矩陣，其為轉(zhuǎn)子自由度的非線性函數(shù)矩陣。

2 基于諧波平衡的非線性模態(tài)求解方法

2.1 諧波平衡法原理

非線性模態(tài)由Rosenberg首次提出，將其定義為無阻尼非線性系統(tǒng)的一種同步周期振子[17]，此后為了能夠考慮系統(tǒng)阻尼耗散，Krack[18]、Laxalde[19]等學者將線性系統(tǒng)復模態(tài)概念進一步擴展，提出了復非線性模態(tài)概念。根據(jù)復非線性模態(tài)概念，動力學方程式(5)的特征值為

(6)

式中：ω0為特征頻率；ξ為模態(tài)阻尼比。此處假設模態(tài)阻尼比是與頻率無關的。

根據(jù)非線性模態(tài)定義，非線性模態(tài)具有周期運動特性，故可以展開成傅里葉級數(shù)形式，但由于系統(tǒng)存在阻尼，需引入慢變的衰減項e-kβt，其中，k=1,2，…,l表示諧波階次，l為諧波系數(shù)總數(shù)，t為時間，則非線性模態(tài)運動表示為

(7)

該非線性模態(tài)運動的基頻即為λ=-β+iω，A0為靜力項，Ak、Bk分別為正弦和余弦展開項的系數(shù)向量。若忽略靜力項并僅保留k=1項，上述解便退化為線性阻尼系統(tǒng)的指數(shù)解假設；若系統(tǒng)為保守系統(tǒng)，即不存在阻尼耗散，則慢變衰減項e-kβt=1。

對于碰摩約束項g(u)=K′(u)u(t)，由于K′(u)為位移u(t)的非線性函數(shù)，故該項也可以展開為傅里葉形式，如式(8)所示：

Pksinkωt)

(8)

式中：P0為碰摩載荷的傅里葉展開常數(shù)項；Pk和Qk為碰摩載荷的傅里葉展開正弦和余弦分量。

將式(6)～式(8)代入到式(5)中，并分別令方程的e-kβtsinkωt和e-kβtcoskωt等于0，整理得到代數(shù)方程：

(9)

KA0+P0=0

(10)

其中:D=C+G。將各個階次的平衡方程進行組裝，得到如下的代數(shù)方程組：

(11)

其中：

Λk=

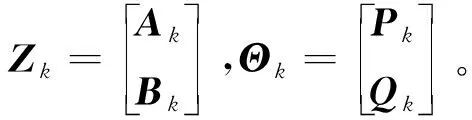
H(Z,ω,β)=Λ(ω,β)Z+b(Z,ω)=0

(12)

其中：

2.2 自由度縮減方法

由于柔性轉(zhuǎn)子系統(tǒng)具有較多的自由度，因此式(12)所示的非線性代數(shù)方程通常具有較高規(guī)模，這將導致代數(shù)方程在求解過程中存在求解效率低、難于收斂問題。為此，給出如下的自由度縮減方法。假設系統(tǒng)非線性自由度個數(shù)為m，線性自由度個數(shù)為s(m+s=N，N為轉(zhuǎn)子系統(tǒng)自由度總數(shù))。對于式(13)所示的非線性代數(shù)方程組，按線性和非線性自由度進行分塊：

(13)

其中：

式(13)進行展開，可得：

ΛqqZq+ΛqpZp+Rq=0

(14)

ΛpqZq+ΛppZp=0

(15)

根據(jù)式(15)，得到Zp的表達式為

(16)

將式(16)代入(14)，得到：

(17)

2.3 數(shù)值求解方法

對前述非線性代數(shù)方程組進行求解，還需解決如下兩方面問題，其一是由于特征值λ=-β+iω的引入，使得非線性代數(shù)方程的待求變量比方程數(shù)量多2，為此，可借鑒線性系統(tǒng)模態(tài)歸一化的思想，引入附加方程，從而使代數(shù)方程組靜定。選取第m個自由度的一次諧波系數(shù)進行歸一化處理，即令：

(18)

第2個問題是如何根據(jù)位移u(t)的傅里葉系數(shù)獲得碰摩項g(u)=K′(u)u(t)的傅里葉系數(shù)，此處通過時頻轉(zhuǎn)換技術予以計算，如式(19)所示，通過位移的各項諧波系數(shù)，可以確定位移的時域表達，根據(jù)時域中碰摩約束項與位移間的顯示關系，確定時域中的碰摩約束項表達，便可以得到碰摩約束項的各項諧波系數(shù)。變換時，傅里葉系數(shù)與其時域間的關系通過離散傅里葉變換與逆變換實現(xiàn)。

(19)

最終，獲得如下的非線性代數(shù)方程：

(20)

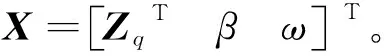
X(k+1)=X(k)-F′(X(k))-1F(X(k))

(21)

計算時，取線性模態(tài)分析結(jié)果作為初值X(0)，F(xiàn)′(X(k))為向量函數(shù)的Jacobi矩陣，通過有限差分法計算得到。

2.4 計算流程

結(jié)合第1節(jié)建模及本節(jié)的計算方法，本文提出求解航空發(fā)動機轉(zhuǎn)子系統(tǒng)非線性模態(tài)的一般流程，如圖5所示。

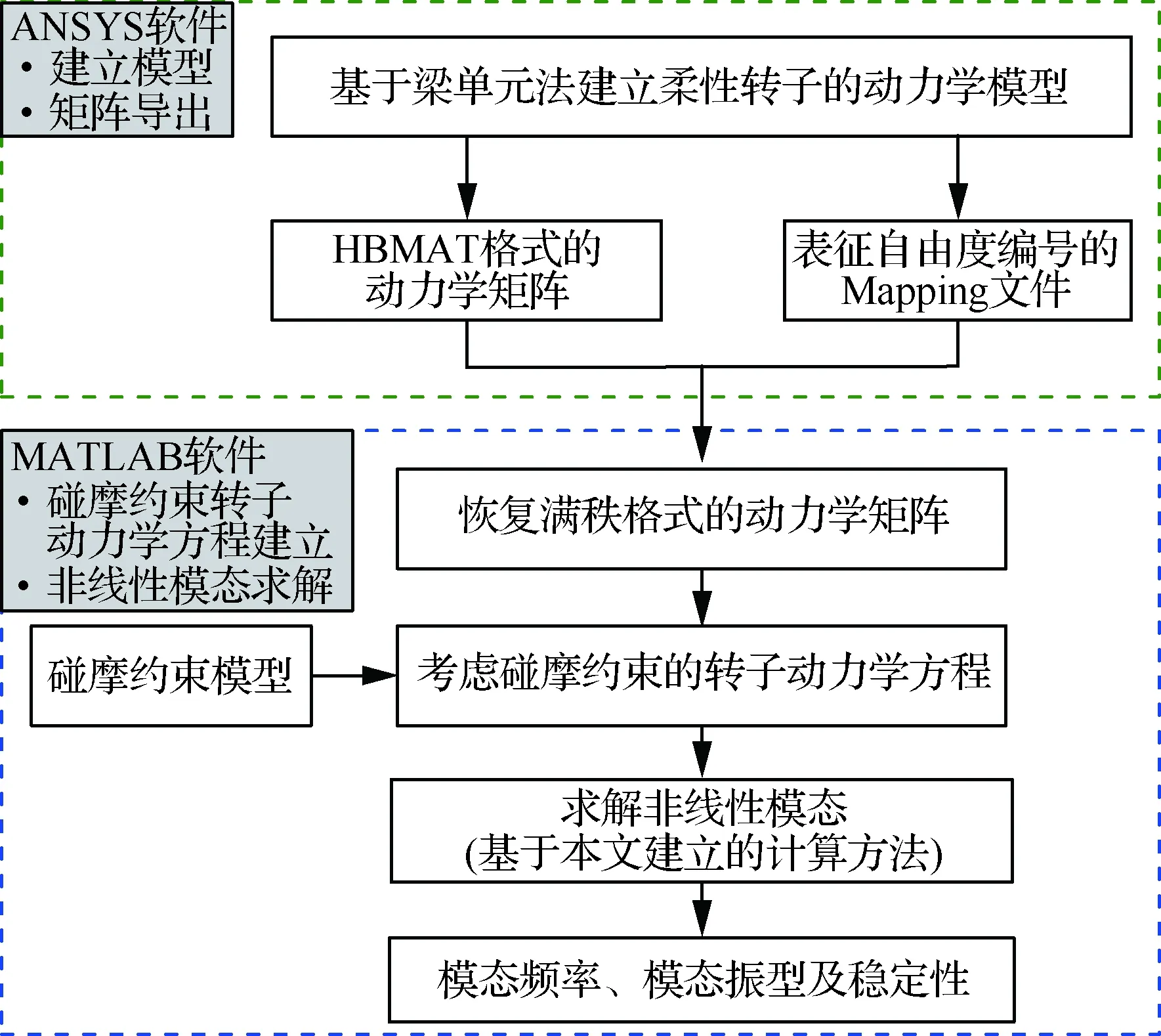
圖5 航空發(fā)動機轉(zhuǎn)子非線性模態(tài)分析流程Fig.5 Modal analysis process for rotor system in aero-engines

首先結(jié)合CAD簡化模型獲得轉(zhuǎn)子截面參數(shù)、質(zhì)量轉(zhuǎn)動慣量參數(shù)等參數(shù)后，基于ANSYS軟件建立其梁單元模型，而后導出HBMAT格式的動力學矩陣(質(zhì)量矩陣、剛度矩陣等)以及Mapping映射文件(含自由度編號信息)；在MATLAB文件中，首先根據(jù)HBMAT格式的動力學矩陣和Mapping文件獲得滿秩格式的動力學矩陣，根據(jù)節(jié)點自由度編號引入碰摩約束項，建立考慮碰摩約束的轉(zhuǎn)子動力學方程，進一步結(jié)合本文建立的轉(zhuǎn)子非線性模態(tài)計算方法，獲得碰摩約束轉(zhuǎn)子的模態(tài)特性。

3 計算結(jié)果與討論

3.1 無碰摩時轉(zhuǎn)子的模態(tài)特性

針對圖3的柔性轉(zhuǎn)子系統(tǒng)，本節(jié)分析其在碰摩約束下的非線性模態(tài)特性。首先了解該轉(zhuǎn)子系統(tǒng)在無碰摩狀態(tài)下的固有特性，根據(jù)第1節(jié)建立的轉(zhuǎn)子模型，基于ANSYS軟件對不同轉(zhuǎn)速下轉(zhuǎn)子進行線性特征值計算，得到各轉(zhuǎn)速下轉(zhuǎn)子線性模態(tài)頻率，圖6和圖7所示分別為相應的坎貝爾圖及兩階正進動臨界轉(zhuǎn)速下的振型，結(jié)果表明：該轉(zhuǎn)子在工作轉(zhuǎn)速范圍內(nèi)存在兩階正/反進動臨界轉(zhuǎn)速，一階正/反進動臨界轉(zhuǎn)速為2 720 r/min和1 480 r/min；二階正/反進動臨界轉(zhuǎn)速為4 660 r/min 和2 210 r/min。對應振型分別為轉(zhuǎn)子一階彎曲和渦輪平動振型。

圖6 無碰摩時柔性轉(zhuǎn)子的坎貝爾圖Fig.6 Campbell diagram of flexible rotor without rub-impact

圖7 兩階臨界轉(zhuǎn)速下轉(zhuǎn)子振型Fig.7 Mode shapes at two order critical speeds

3.2 碰摩影響下轉(zhuǎn)子模態(tài)特性

考慮風扇碰摩對轉(zhuǎn)子模態(tài)特性的影響，給定如下計算參數(shù)：機匣剛度kc=107N/m，摩擦系數(shù)μ=0.2，轉(zhuǎn)靜間隙r0=0.2 mm，葉盤直徑800 mm，轉(zhuǎn)子1#支點存在阻尼，值為10 000 N·s/m，同時假設轉(zhuǎn)子工作于巡航轉(zhuǎn)速3 600 r/min。由于非線性模態(tài)具有能量相關性，需考慮不同振動狀態(tài)下轉(zhuǎn)子模態(tài)，本文通過風扇幅值大小來反映轉(zhuǎn)子振動水平，在2.3節(jié)的模態(tài)歸一化中給定不同的風扇幅值，而后基于2.4節(jié)計算流程獲得不同風扇幅值下轉(zhuǎn)子模態(tài)頻率，結(jié)果如圖8所示。本文在分析中主要考慮工作轉(zhuǎn)速范圍內(nèi)的兩階模態(tài)，圖中結(jié)果可得出如下結(jié)論：

1) 轉(zhuǎn)子振動水平較小時，風扇幅值小于轉(zhuǎn)靜間隙，未發(fā)生碰摩，通過本文非線性模態(tài)求解方法計算得到的模態(tài)頻率與圖6中ANSYS線性特征值計算結(jié)果進行對比，2種方法計算結(jié)果相同，側(cè)面驗證了本文建立的非線性模態(tài)計算方法的有效性。

2) 當風扇幅值超過轉(zhuǎn)靜間隙時，風扇機匣約束使得轉(zhuǎn)子各階正/反進動模態(tài)頻率增加，增加趨勢呈現(xiàn)逐漸變緩趨勢，當風扇振幅達到一定程度，即轉(zhuǎn)子振動能量足夠高時，轉(zhuǎn)子各階模特頻率趨近于定值。總體而言，考慮碰摩約束影響時轉(zhuǎn)子模特頻率具有區(qū)間分布特征，不同振動狀態(tài)下轉(zhuǎn)子模態(tài)頻率均位于該區(qū)間內(nèi)。

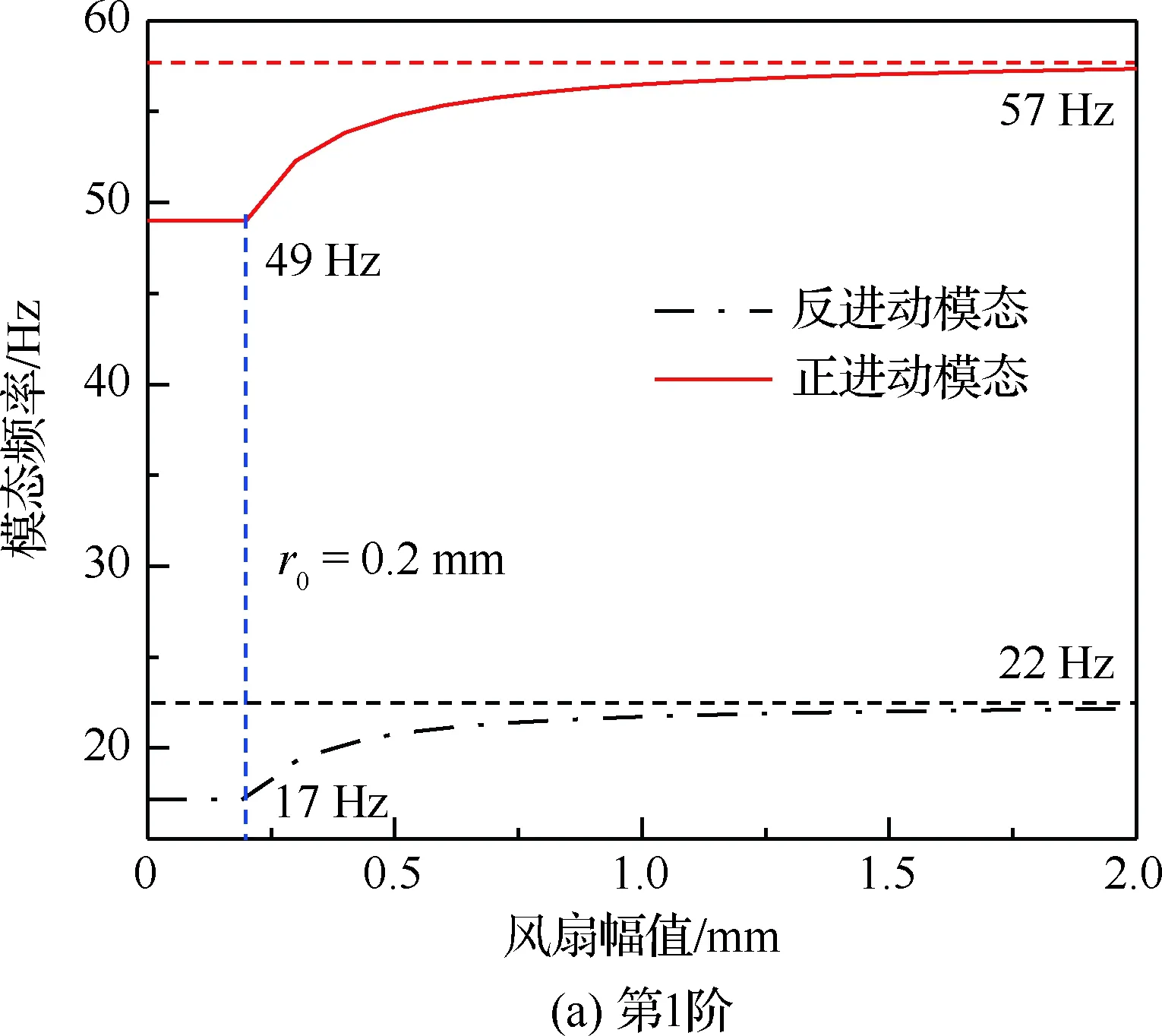
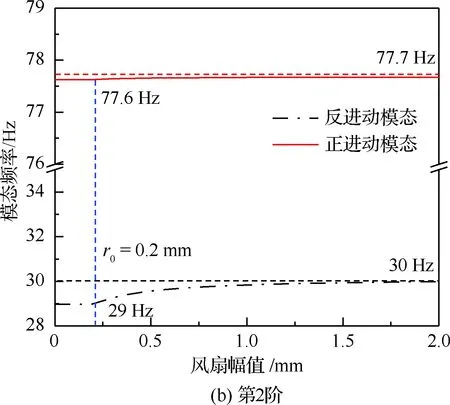
圖8 風扇碰摩對兩階模態(tài)頻率的影響(巡航轉(zhuǎn)速3 600 r/min)Fig.8 Influence of fan rubbing on two order modal frequencies (Operating speed 3 600 r/min)

表1 不同風扇相對幅值下轉(zhuǎn)子模態(tài)頻率的變化率

以上分析了碰摩約束轉(zhuǎn)子在特定轉(zhuǎn)速下的模態(tài)，針對不同轉(zhuǎn)速，分別計算轉(zhuǎn)子模態(tài)頻率隨振幅變化曲線，提取各轉(zhuǎn)速下轉(zhuǎn)子模態(tài)頻率區(qū)間最小值和最大值，如圖9所示，進而可獲得碰摩約束轉(zhuǎn)子的各階臨界轉(zhuǎn)速。結(jié)果表明：風扇碰摩下，轉(zhuǎn)子一階正/反進動臨界轉(zhuǎn)速區(qū)間分別為[2 720,3 460]r/min和[1 480,1 810]r/min；二階正/反進動臨界轉(zhuǎn)速區(qū)間分別為[4 660,4 683]r/min和[2 210,2 260]r/min，風扇振動為主的一階臨界轉(zhuǎn)速受風扇碰摩約束改變較為顯著，使得該階臨界轉(zhuǎn)速相對巡航轉(zhuǎn)速裕度顯著降低。航空發(fā)動機對氣動效率的高要求，葉尖間隙通常接近零間隙設計，工作時碰摩時常發(fā)生，臨界轉(zhuǎn)速分析結(jié)果說明實際工程中考慮碰摩約束帶來的轉(zhuǎn)子臨界轉(zhuǎn)速及其裕度是極其必要的。

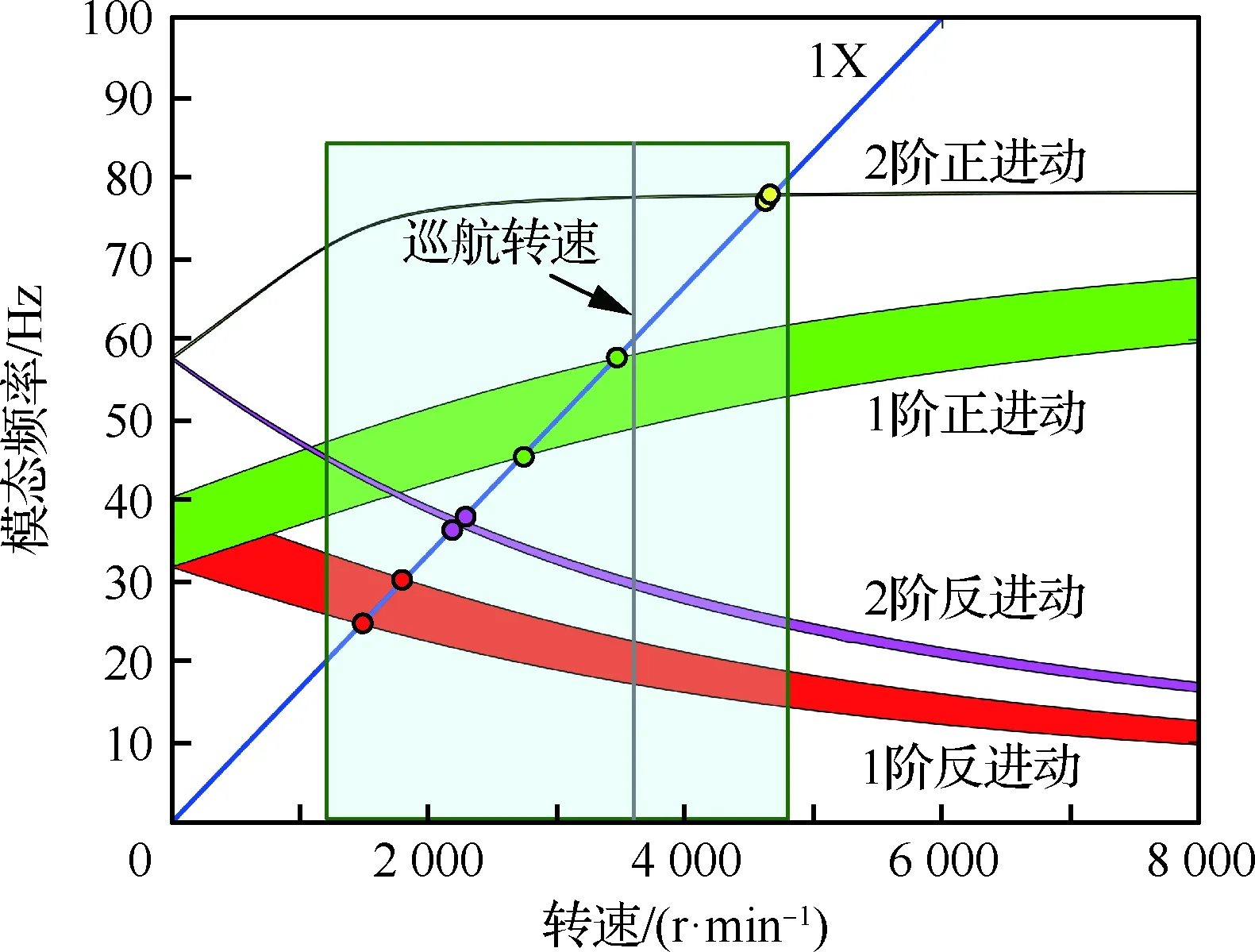
圖9 風扇碰摩約束下轉(zhuǎn)子系統(tǒng)坎貝爾圖Fig.9 Campbell diagram of rotor system with fan rub-impact

圖10所示為碰摩約束對轉(zhuǎn)子振型的影響，圖中碰摩約束下的轉(zhuǎn)子振型均取模態(tài)頻率接近極限值(風扇振幅2 mm)時的結(jié)果，同時為便于對比，將無碰摩時和碰摩時的振型均作振幅歸一化，兩階振型均取遠離風扇碰摩位置的渦輪作為基準進行歸一化。結(jié)果表明：碰摩對轉(zhuǎn)子振型產(chǎn)生一定影響，對于風扇振動為主的一階模態(tài)，風扇碰摩約束可使得風扇位置的相對振動幅值有所降低，即抑制了風扇振動；而對于渦輪振動為主的二階模態(tài)，風扇碰摩約束使得風扇相對振動略有增加，二階振型存在由渦輪振動向低壓轉(zhuǎn)子二階彎曲演化的趨勢，但總體而言風扇碰摩約束對二階振型的影響相對較小。

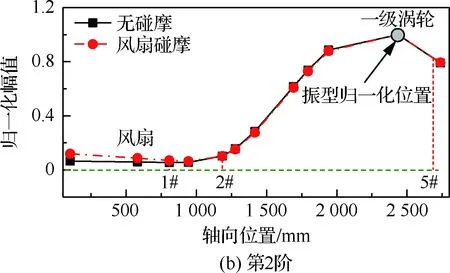
圖10 風扇碰摩約束對轉(zhuǎn)子振型的影響Fig.10 Influence of fan rub-impact on rotor modal shapes

根據(jù)2.1節(jié)，轉(zhuǎn)子模態(tài)阻尼對應著特征值實部，其決定著模態(tài)運動隨時間的衰減速率。對于大多數(shù)線性系統(tǒng)，模態(tài)阻尼通常為正，系統(tǒng)模態(tài)運動隨時間衰減，而對于非線性系統(tǒng)，非線性力的引入可能導致模態(tài)阻尼為負，因而其模態(tài)并不總是穩(wěn)定的。圖11所示為轉(zhuǎn)子各階模態(tài)阻尼比隨轉(zhuǎn)子振動幅值的變化曲線，結(jié)果表明：未碰摩時，轉(zhuǎn)子各階模態(tài)阻尼比為正，其原因是由于1#支點存在阻尼；當風扇振幅超過轉(zhuǎn)靜間隙時，轉(zhuǎn)靜件發(fā)生碰摩，各階模態(tài)阻尼比將發(fā)生變化，對于正進動模態(tài)，其模態(tài)阻尼比隨振幅增加，而反進動模態(tài)阻尼則隨振幅減小，當碰摩足夠劇烈時，轉(zhuǎn)子系統(tǒng)的

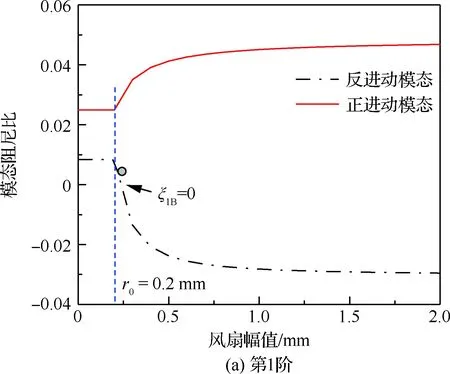
反進動模態(tài)阻尼比為負，此時反進動模態(tài)不穩(wěn)定。正反進動模態(tài)阻尼的變化機理主要與碰摩接觸點處摩擦力做功有關[14]，對于反進動模態(tài)，摩擦力對轉(zhuǎn)子系統(tǒng)的模態(tài)運動做正功，增加轉(zhuǎn)子能量，導致反進動模態(tài)阻尼比下降，當摩擦力輸入能量超過轉(zhuǎn)子支點阻尼耗散能力時，轉(zhuǎn)子等效模態(tài)阻尼比為負，此時模態(tài)失穩(wěn)。需要說明的是，由反進動模態(tài)不穩(wěn)定誘發(fā)的轉(zhuǎn)子振動響應失穩(wěn)現(xiàn)象已在簡單轉(zhuǎn)子試驗器上得到了證實[3]。然而，在實際航空發(fā)動機轉(zhuǎn)子中，反進動模態(tài)不穩(wěn)定導致的轉(zhuǎn)子振動失穩(wěn)卻鮮有出現(xiàn)，主要原因可能在于航空發(fā)動機轉(zhuǎn)子中通常具有擠壓油膜阻尼器，同時轉(zhuǎn)子中大量連接界面的存在等，使得轉(zhuǎn)子系統(tǒng)具有足夠的相對阻尼，因此轉(zhuǎn)子系統(tǒng)的振動能量能夠得到有效的耗散。

3.3 碰摩參數(shù)的影響規(guī)律

實際工程中，航空發(fā)動機風扇機匣可能采用不同材質(zhì)并內(nèi)涂不同材質(zhì)/硬度的涂層[20]，這對機匣自身剛度以及葉片/機匣之間的摩擦系數(shù)有明顯影響。因此，本節(jié)重點分析機匣剛度和摩擦系數(shù)對碰摩轉(zhuǎn)子模態(tài)特性的影響。

3.3.1 機匣剛度

機匣剛度分別取5×106N/m、1×107N/m和2×107N/m，其他參數(shù)與3.1節(jié)相同。計算得到不同機匣剛度下，轉(zhuǎn)子兩階正/反進動模態(tài)頻率隨振幅變化曲線，如圖12所示。可以看出，隨機匣剛度增加，轉(zhuǎn)子兩階正/反進動模態(tài)頻率均增加，其原因是在相同振動狀態(tài)下，機匣剛度越高，其對

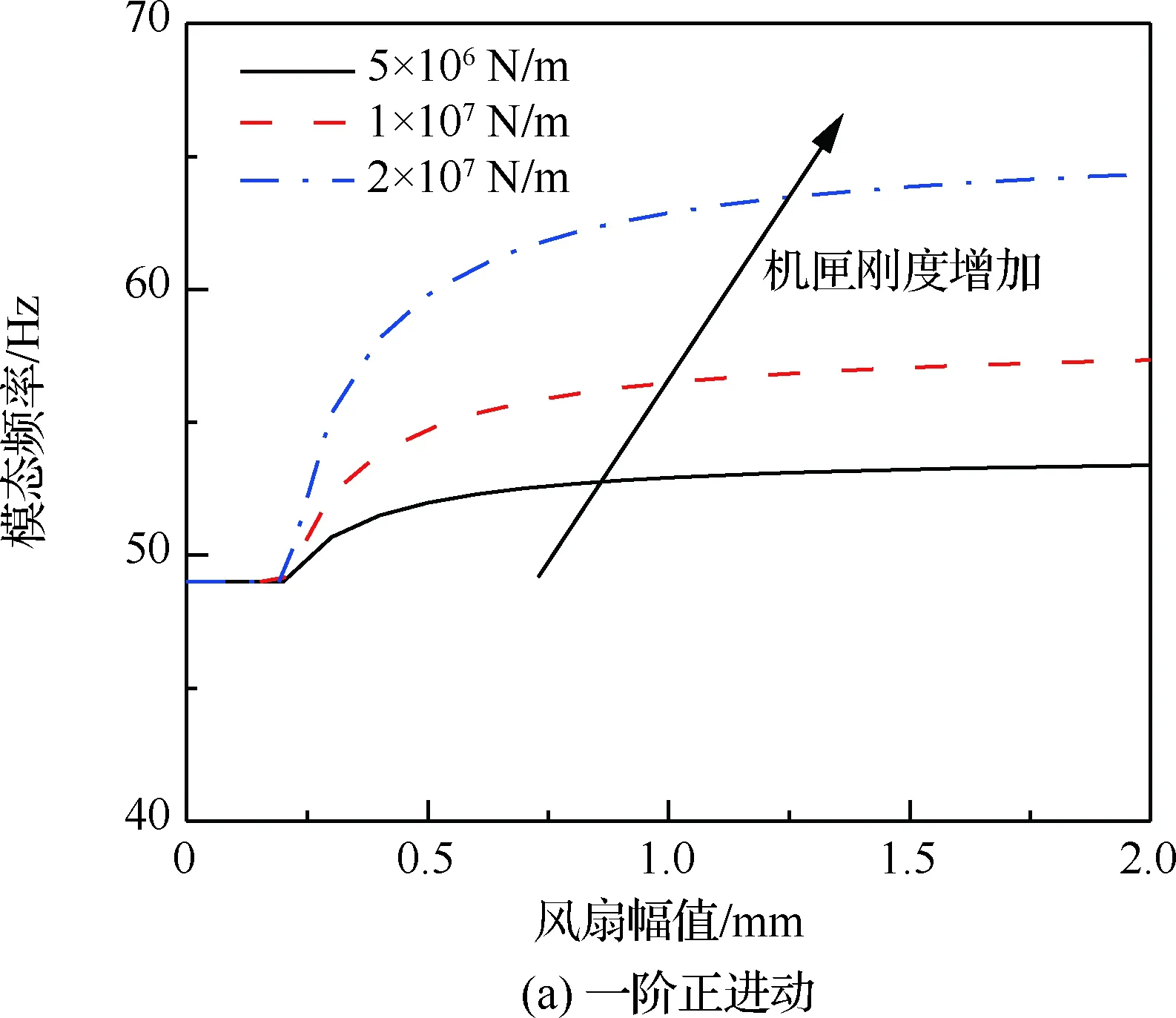
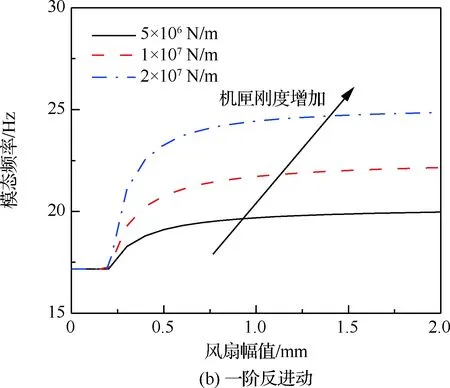
圖12 機匣剛度對模態(tài)頻率的影響Fig.12 Influence of casing stiffness on modal frequency

轉(zhuǎn)子系統(tǒng)的約束作用越強，導致模態(tài)頻率增加的越高。另外，從機匣剛度對兩階模態(tài)頻率影響的相對變化而言，如表2所示，一階模態(tài)頻率對碰摩剛度變化更為敏感，而二階模態(tài)頻率對碰摩剛度變化則極不敏感，以兩階正進動模態(tài)頻率為例，當碰摩剛度由5×106N/m增加至2×107N/m，一階正進動

表2 不同碰摩剛度下柔性轉(zhuǎn)子系統(tǒng)模態(tài)頻率變化率(風扇幅值2 mm)

模態(tài)頻率變化率可由8.94%增加至31.49%；而二階正進動模態(tài)頻率變化率由0.06%增加至0.19%。

由于反進動模態(tài)存在失穩(wěn)的可能，因此分析機匣剛度對反進動模態(tài)阻尼的影響，如圖13所示，可以看出：隨機匣剛度增加，反進動模態(tài)阻尼比等于0的臨界振幅逐漸減小，表明機匣剛度越高，碰摩時反進動模態(tài)越容易失穩(wěn)。

圖14所示為不同機匣剛度下低壓轉(zhuǎn)子的振型，不同機匣剛度下轉(zhuǎn)子振型均相對渦輪進行了振幅歸一化處理。結(jié)果表明：① 對于風扇振動為主的一階彎曲振型，隨著機匣剛度增加，風扇位置的相對振幅逐漸增加，表明機匣剛度越高，對風扇振動的抑制作用愈發(fā)明顯；② 對于渦輪振動為主的二階振型，隨著機匣剛度增加，風扇相對振幅有增加的趨勢，低壓轉(zhuǎn)子向二階彎曲振型演化的趨勢愈發(fā)顯著。

圖14 機匣剛度對模態(tài)振型的影響Fig.14 Influence of casing stiffness on modal shapes

3.3.2 摩擦系數(shù)

本節(jié)分析摩擦系數(shù)對轉(zhuǎn)子模態(tài)特性的影響，如前所述，風扇碰摩對轉(zhuǎn)子一階模態(tài)頻率的影響顯著高于二階模態(tài)，故此處僅一階反進動模態(tài)為例，給出計算結(jié)果。圖15所示為摩擦系數(shù)取0.1、 0.2和0.4時，一階反進動模態(tài)頻率和阻尼變化曲線。結(jié)果表明，摩擦系數(shù)對轉(zhuǎn)子模態(tài)頻率的影響極小，表明轉(zhuǎn)子模態(tài)頻率主要取決于接觸點處法向約束，而對切向的摩擦作用極不敏感；而對于反進動模態(tài)阻尼，隨摩擦系數(shù)增加，轉(zhuǎn)子反進動模態(tài)阻尼比顯著下降，同時模態(tài)阻尼比等于0的臨界振幅逐漸減小，表明摩擦系數(shù)越高，反進動模態(tài)越容易失穩(wěn)。

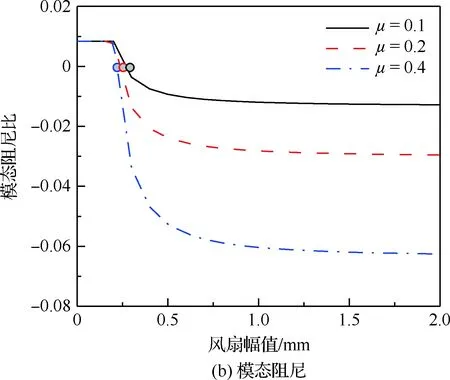
圖15 摩擦系數(shù)對轉(zhuǎn)子一階反進動模態(tài)的影響Fig.15 Influence of friction coefficient on first order backward whirl mode

4 結(jié) 論

1) 本文針對航空發(fā)動機中具有復雜結(jié)構和質(zhì)量/剛度分布的柔性轉(zhuǎn)子系統(tǒng)，結(jié)合梁單元法提出了可考慮碰摩約束的復雜轉(zhuǎn)子系統(tǒng)動力學建模方法；將諧波平衡思想與頻域的自由度縮減技術結(jié)合，建立了適用于復雜非線性轉(zhuǎn)子系統(tǒng)非線性模態(tài)特性的求解方法；基于ANSYS和MATLAB平臺，將建模方法與求解方法融合，提出了可適用于工程中含大規(guī)模自由度的非線性轉(zhuǎn)子系統(tǒng)模態(tài)特性的計算分析流程。建模及求解方法的適用性在某航空發(fā)動機柔性轉(zhuǎn)子系統(tǒng)的非線性模態(tài)分析中得到了驗證。

2) 碰摩約束使轉(zhuǎn)子系統(tǒng)模態(tài)頻率/臨界轉(zhuǎn)速顯著增加，且轉(zhuǎn)子振幅越高，機匣對轉(zhuǎn)子約束作用越強，模態(tài)頻率也越高，針對文中所分析的發(fā)動機柔性轉(zhuǎn)子對象及參數(shù)，風扇碰摩可使一階彎曲型的正/反進動模態(tài)頻率最高增加約16%和29%。但需要注意的是，碰摩約束轉(zhuǎn)子的模態(tài)頻率始終位于特定區(qū)間范圍內(nèi)。此外，風扇碰摩同時對轉(zhuǎn)子一階彎曲型的模態(tài)振型產(chǎn)生一定抑制作用。陀螺效應、轉(zhuǎn)子振型以及機匣剛度對碰摩約束帶來的轉(zhuǎn)子模態(tài)頻率變化有較為顯著的影響，但摩擦系數(shù)的影響可以忽略。

3) 由于碰摩點處切向摩擦力做功影響，碰摩對轉(zhuǎn)子系統(tǒng)模態(tài)阻尼亦會產(chǎn)生顯著影響，轉(zhuǎn)子各階正進動模態(tài)阻尼始終大于0，而反進動模態(tài)阻尼在碰摩較為劇烈時可能小于0，表明碰摩轉(zhuǎn)子的正進動模態(tài)始終穩(wěn)定，而反進動模態(tài)存在失穩(wěn)的可能。結(jié)合模態(tài)阻尼變化機理及關鍵參數(shù)影響規(guī)律，實際中通過擠壓油膜阻尼器提升轉(zhuǎn)子系統(tǒng)的阻尼耗散能力、抑制碰摩程度等方式均可降低反進動模態(tài)失穩(wěn)的可能性。

與線性模態(tài)類似，非線性模態(tài)為非線性轉(zhuǎn)子系統(tǒng)的一種固有特性，必然在理解轉(zhuǎn)子非線性振動響應方面能發(fā)揮重要作用。本文揭示了碰摩約束對航空發(fā)動機低壓轉(zhuǎn)子非線性模態(tài)的影響，進一步，碰摩轉(zhuǎn)子的非線性模態(tài)與其振動響應之間的影響關系如何，例如非線性模態(tài)在何種運動狀態(tài)下被激起,不同階次的非線性模態(tài)對碰摩轉(zhuǎn)子動力學行為的演化有何貢獻,這些理論問題將在未來予以重點關注。