基于改進粒子群算法辨識Volterra級數的目標機動軌跡預測
奚之飛,徐安,寇英信,李戰武,楊愛武
空軍工程大學 航空工程學院,西安 710038
軌跡預測是根據目標的歷史運動軌跡,學習和推理其包含的內在信息,進而對目標未來的運動趨勢作出合理推測的過程。在空空對抗作戰過程中,對敵方目標的機動軌跡作出合理的預測具有重要意義。基于包伊德循環(Observe、Orientation、Decide and Act,OODA)理論可知,空戰取勝的關鍵是先敵形成OODA環,從而對敵實現“先敵發現”“先敵調整”“先敵決策”以及“先敵攻擊”,達到先發制人的目的[1],實現這一系列行為的基礎是對目標機動軌跡實現精確預測,故研究目標機動軌跡預測具有重要意義。
近幾年,對于目標機動軌跡預測方法的研究方向主要分為兩大類。一類是側重于卡爾曼濾波算法的傳統預測方法。卡爾曼濾波算法能夠對目標的運動狀態進行最優估計并且能夠實現實時狀態估計和預測,適用于有限維度的線性和非線性的目標時空運動軌跡。例如文獻[2]針對目標運動模式變化多以及機動幅度較大的情況,提出一種基于多項式卡爾曼濾波的運動軌跡預測算法;文獻[3]針對歷史位置信息存在缺失的情況,提出一種具有系統噪聲估計的改進卡爾曼濾波算法對目標機動軌跡進行預測;文獻[4]針對傳統軌跡預測算法已無法滿足高精度和實時性預測要求,提出一種基于卡爾曼濾波的動態軌跡預測算法;文獻[5]針對精確高階目標運動模型存在的高度非線性,數據處理難度大以及預測精度低等問題,提出一種改進的交互多模型軌跡預測算法。上述預測算法都只適用于目標運動特性相對簡單的軌跡預測問題,但是在空戰過程中,目標的運動往往是高度復雜的時序過程,傳統的軌跡預測算法不能準確地學習目標的機動特性,同時也存在建模復雜度高和算法的適應性差的問題,且卡爾曼濾波算法的狀態和測量方程的推導很困難,算法的預測精度也不能滿足空戰對抗需求。
另一類研究方向主要以神經網絡算法為主的人工智能算法,結合大數據建立目標機動軌跡預測模型。例如文獻[6]利用廣義回歸神經網絡(Generalized Regression Neural Network,GRNN)良好的非線性映射能力以及高度的容錯性和魯棒性,提出一種基于GRNN的高超聲速飛行器軌跡預測算法;針對前饋(Back Propagation,BP)神經網絡存在對初值敏感且全局搜索能力較差的問題,文獻[7-8]分別提出一種基于遺傳算法和粒子群算法優化BP神經網絡的預測模型。但是,文獻[9]提出目標機動軌跡預測問題本質上是動態數據的時間序列預測,具有高度的非線性和時變特性,而傳統的BP神經網絡是一種靜態的單層前饋神經網絡,對于不斷變化的非線性目標機動軌跡時間序列的預測效果相對較差,同時BP神經網絡還存在易陷入極值和過擬合的問題,因而將神經網絡應用于目標機動軌跡預測的效果較差。此外,基于神經網絡的預測方法需要預先建立時間序列的主觀預測模型,確定模型的輸入輸出以及隱含層結構,然后根據建立的主觀預測模型進行計算及預測。隨著混沌理論的發展,可不必預先建立主觀預測模型,而是基于樣本數據時間序列本身所蘊含的客觀規律進行預測,這樣完全可以避免人為主觀性對預測結果造成的影響,從而提高了預測精度和可信度。根據混沌理論,對于某一混沌系統來說,可采用混沌預測模型來進行預測,并且能夠獲得較高的預測精度。因此,本文引入混沌理論的方法來對目標機動軌跡進行建模和預測。基于上述預測思想,首要需要確定目標機動軌跡時間序列是否具有混沌特性。
近些年,混沌時間序列建模及預測已經成為混沌研究領域中的熱點研究方向。目前,基于混沌理論對風功率的研究較多,但是針對基于混沌時間序列建模進行目標機動軌跡預測的研究尚未出現。由混沌理論可知,混沌信號經過相空間重構之后,會得到一個嵌入空間的低維流形,利用其可對重構的時間序列進行預測[10]。此外,Volterra級數預測模型是近些年發展起來的一種預測模型[11],理論和實踐表明,Volterra級數模型可以很好地表征非線性系統,可以對任何非線性函數進行逼近,并且能夠對混沌吸引子的軌跡進行跟蹤,可實現對未來變化趨勢的精確預測。為了更好地處理目標機動軌跡存在的非線性和時變特性,將Volterra級數模型引入到目標機動軌跡時間序列預測中,從而實現對目標未來機動軌跡的精確預測。利用Volterra泛函級數模型進行目標機動軌跡預測的關鍵在于辨識其核函數,然而,Volterra級數核函數辨識存在一個難點,即核參數的數量隨著Volterra級數核階數呈指數增長,計算困難。目前Volterra泛函級數參數辨識的方法主要有最小二乘算法[12-13]、最小均方(Least Mean Square,LMS)算法、遞歸最小二乘法(Recursive Least Square,RLS)以及智能啟發式優化算法[14-18],但是,最小二乘法在辨識參數時要求目標函數連續可導,且采用梯度信息進行搜索時容易陷入局部極值;基于LMS和RLS的全耦合和部分耦合確定Volterra級數核參數的算法收斂性、穩定性以及辨識有效性都不是很好。上述這些傳統算法都存在計算復雜、辨識精度低以及算法收斂速度慢等不足。為了克服傳統算法存在的不足,本文采用仿生智能算法辨識Volterra級數核參數。
粒子群算法是一種模擬生物行為的群智能優化算法[19-20],具有結構簡單且易于實現、容易收斂且魯棒性較強的優點[21]。粒子群算法為求解復雜系統優化問題提供了一種通用框架,該算法不依賴于問題的具體領域,對問題的種類適應性很強,而Volterra級數核函數辨識實質上是一個高維度參數優化問題,因此,本文將粒子群算法引入到Volterra泛函級數模型的核函數參數辨識中,該算法不僅可以避免傳統算法要求待優化函數必須滿足連續可導的缺點,還可以得到很好的優化效果和魯棒性。
文獻[22]通過研究發現,基于基本的粒子群算法對Volterra級數核函數進行辨識時,在算法搜索后期,粒子容易聚集,導致算法容易陷入最優解;同時,對于Volterra級數核函數進行辨識是一個高維度優化問題,粒子群算法在優化高維度問題時,容易出現早熟現象,導致算法陷入局部最優而無法跳出,同時還存在收斂精度不高的問題[23]。基于上述分析,為了同時提高算法的優化性能和避免陷入局部極值點,本文引入一種基于混沌變異和自適應策略優化的粒子群算法,并將改進的粒子群算法(Modified Particle Swarm Optimization algorithm,MPSO)用于Volterra泛函模型參數辨識,構建一種基于改進粒子群算法辨識的Volterra級數目標機動軌跡預測模型。通過仿真實驗,該模型的預測性能優于基于標準粒子群算法、遺傳算法、蟻群算法辨識的Volterra級數預測模型,同時也驗證了該預測算法的有效性和魯棒性。
1 混沌特性分析及相空間重構
1.1 混沌特性分析
檢驗時間序列是否具有混沌特性的算法主要有最大Lyapunov指數法、G-P(Grassberger-Procaccia)算法以及0-1檢測法等。最大Lyapunov指數法在確定時間序列是否具有混沌特性時,需要預先計算時間序列的平均最大周期、嵌入維數和延遲時間,目前確定每一個參數的算法有很多種,但是不同的方法得到的參數并不一致,由于缺乏相應的客觀評判依據,對于參數選擇難度較大,同時算法的計算復雜度高,實時性差;G-P算法通過估算出數據的關聯維數來判定時間序列的混沌特性,該算法容易受到時間序列長度和數據噪聲的影響,隨機噪聲也會對其造成一定的影響,故判讀結果可信程度不高。0-1檢測法不需要確定相空間重構參數,直接輸入離散時間序列即可,不需要預先確定其他參數,最后通過算法返回的數值趨近于0和1來判定輸入時間序列是否具有混沌特性,同時,0-1檢測法適用于含有噪聲時間序列,且計算量小,所需時間短,可以實現快速判斷時間序列的混沌性。
本文主要借鑒0-1檢測法[24-25]對目標機動軌跡時間序列x(n)∈{x(1),x(2), …,x(N)}進行混沌特性判定,此算法不需要對時間序列進行相空間重構預處理,可以直接對時間序列進行混沌特性檢測,算法具體流程如下:
1) 計算平移變量pc(n)和qc(n),即
(1)
(2)
式中:n=1, 2, …,N;c∈(0,π)。
2) 計算變量pc(n)和qc(n)的均方位移Mc(n),即
[qc(i+n)-qc(i)]2}
(3)
3) 根據均方位移計算漸進增長率Kc,即
(4)
4) 重復步驟1)~3),循環計算時間序列的均值K。
時間序列混沌特性判定的準則是:當均值滿足K≈1時,則說明該時間序列具有混沌特性;當均值滿足K≈0,則說明該時間序列不具有混沌特性。本文通過仿真計算得到目標機動軌跡的三維坐標時間序列的均值K分別為KX=0.998 1,KY=0.986 7,KZ=0.963 4。基于判定準則可知,目標機動軌跡的三維坐標時間序列均具有混沌特性。
1.2 相空間重構
相空間重構是分析混沌時間序列的關鍵環節,能夠挖掘出時間序列中所蘊含的信息,根據Takens嵌入延遲定理[26],選擇合適的時間延遲τ和相空間重構嵌入維數m可以獲得與原系統具有相同的動態特性的新系統。對一維時間序列x(n)進行相空間重構,得到的多維時間序列為
(5)
則相空間重構之后多維空間的相點數Np為
Np=N-(m-1)τ
(6)
1.3 基于改進C-C法確定相空間重構參數
在對混沌時間序列進行分析時,時間延遲和嵌入維數的確定,直接關系到能否充分反映原始時間序列的特性變化[27]。針對傳統C-C法在求解時間延遲和嵌入維度存在的不足,本文采用改進的C-C法[28]來確定相空間重構相關參數,使得計算結果更加準確。
定義關聯積分為
(7)
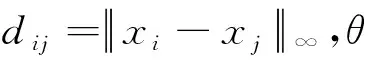
定義檢驗統計量為
S1(m,N,r,τ)=C(m,N,r,τ)-Cm(1,N,r,τ)
(8)
在計算檢驗統計量時,采用劃分子時間序列的計算方法,即
S2(m,N,r,τ)=
(9)
定義差量為:
ΔS(m,N,r,τ)=
max{S(m,N,r,τ)}-min{S(m,N,r,τ)}
(10)

(11)
(12)
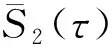
m=τw/τ+1
(13)
2 Volterra級數模型
對于輸入為x(k)和輸出為y(k)的離散時間非線性動態系統,通過Volterra級數模型可將其描述為[29]
(14)
(15)
式中:e(k)為Volterra級數截斷誤差;hn(m1,m2,…,mn)為非線性系統的n階Volterra級數核函數,核函數具有對稱性且對稱性是唯一的[29]。在確定Volterra級數核函數的過程中,充分利用其對稱性可以大大減小Volterra級數模型的計算量。
利用截斷的Volerra級數可以精確近似描述很多非線性系統,在對非線性進行描述時,一般采取前三階的截斷形式,故通常是對Volterra級數模型的前三階核函數進行辨識[29]。根據Volterra級數核函數所具備的對稱特性以及Volterra級數表達形式,可將系統的輸出表達為
h2(m1,m2)x(k-m1)x(k-m2)+
x(k-m1)x(k-m2)x(k-m3)+e(k)
(16)
式中:Mi為模型的記憶長度,當Mi取合適的值時,截斷誤差e(k)可以充分小,在誤差允許的范圍內,e(k)可以忽略不計;s1(m1)、s2(m1、m2)、s3(m1、m2、m3)由式(17)~式(19)確定:
s1(m1)=1
(17)
(18)
s3(m1,m2,m3)=
(19)
假設Volterra級數模型截斷的最高階數為NT,假設系統的輸入矩陣為
P=[X(k),X(k+1), …,X(k+L-1)]T
(20)
式中:L為輸入數據的長度。則k時刻的截斷Volterra級數系統輸入向量可表示為
X(k)=[x(k),x(k-1),…,x(k-M1+1),
x2(k),x(k)x(k-1), …,
xN(k-MNT+1) ]T
(21)
此時,截斷Volterra級數系統輸出向量以及核函數可表示為
Y=[y(k),y(k+1),…,y(k+L-1)]T
(22)
H=[h1(0),h1(1),…,h1(M1-1),h2(0,0),
h2(0,1), …,hN(MN-1, …,MN-1)]T
(23)
式中:X(k)為輸入向量;Y為輸出向量;H為Volterra級數的核函數。基于上述表達可將系統表述為
Y=PH+e
(24)
式中:e為誤差。由式(24)可知,基于截斷Volterra級數模型的非線性系統辨識,就是在確定的系統輸入和輸出的基礎上確定Volterra級數的核函數向量H。Volterra級數系統辨識實際上是一個最優化參數估計問題,本文采取一種基于混沌變異和自適應策略優化的粒子群算法來解算Volterra級數核函數向量。
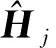
(25)
式中:L為數據長度,j=1, 2, …,n。對于粒子群中第j個粒子的速度和位置進化規則為
vj(t+1)=ωj(t)vj(t)+
(26)
(27)

改進的粒子群算法在尋優的過程中,通過不斷搜索尋找使得式(27)所示的目標函數值最小的全局最優位置,即Volterra級數核矢量的最佳辨識結果。
3 基于改進粒子群算法辨識的Volterra級數預測模型
3.1 改進的粒子群算法
通過對文獻中粒子群算法研究發現,目前大多數的文獻未能充分發揮粒子群算法的優良性能,也未能充分考慮粒子群算法的性能與算法進程之間的關系,從而在一定程度影響了算法的收斂速度和尋優效率;同時,在算法的尋優過程中由于粒子群存在容易聚集的特點,種群的多樣性難免會降低,因而可能會導致算法存在容易陷入局部極值、早熟的不足。
針對目前粒子群算法存在的不足,本文主要從3個方面來改進基本的粒子群算法:
1) 利用混沌具有的良好的隨機性、便利性以及規律性等特點,對粒子群進行初始化操作。
2) 依據粒子群的進化進程的不同,采取不同的算法來改進粒子群算法,在進化的過程中將粒子群劃分為精英子種群和普通子種群,同時對各個子種群采取不同的參數自適應調整策略,從而達到增加種群多樣性、實現全局和局部搜索能力相平衡的效果。
3) 為了更好地發揮粒子群算法的尋優性能,實時判斷算法是否陷入局部最優解,當算法陷入局部最優解時對粒子進行混沌變異操作。
3.1.1 基于混沌映射初始化粒子群
在不改變粒子群算法隨機初始化時所具有的良好性能前提下,采用混沌映射對粒子群進行初始化,混沌映射可以有效地提高粒子種群的多樣性。文獻[30-32]通過對比分析得出Tent映射模型比Logisitic映射模型具有更高的搜索效率的結論,同時也驗證了Tent映射可以更好地改善粒子群的多樣性以及算法的尋優能力。本文采用Skew-Tent映射模型對粒子群進行初始化操作,具體的Skew-Tent混沌映射模型為
xk+1=g(xk)
(28)
(29)
式中,當參數φ在[0,1]取值,并且x∈[0,1]時,式(25)和式(26)所描述的系統處于混沌轉態。利用Skew-Tent混沌映射對粒子群進行初始化的具體流程如算法1所示。

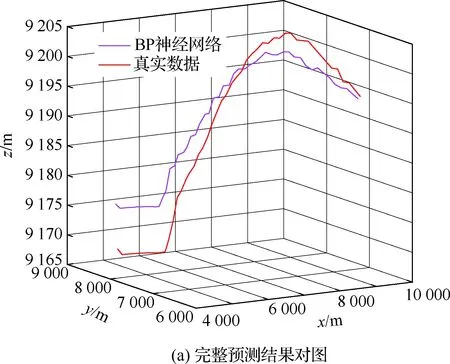
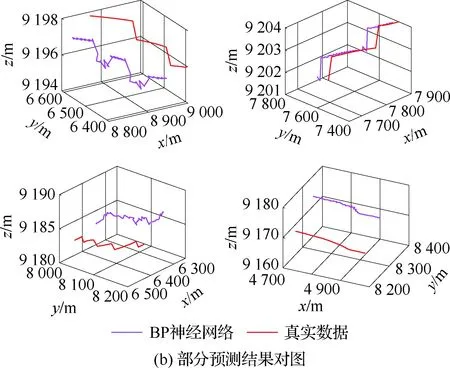
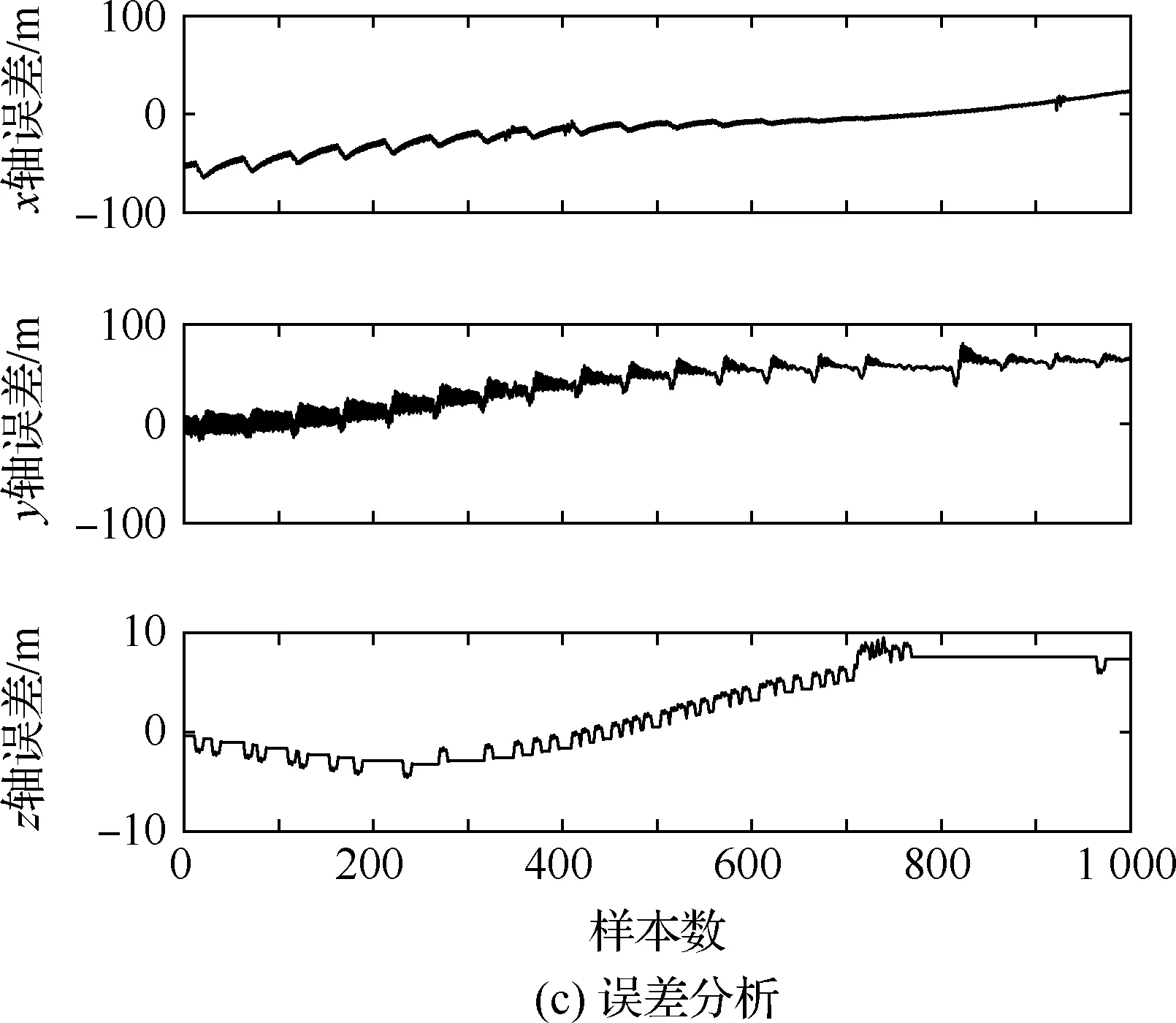
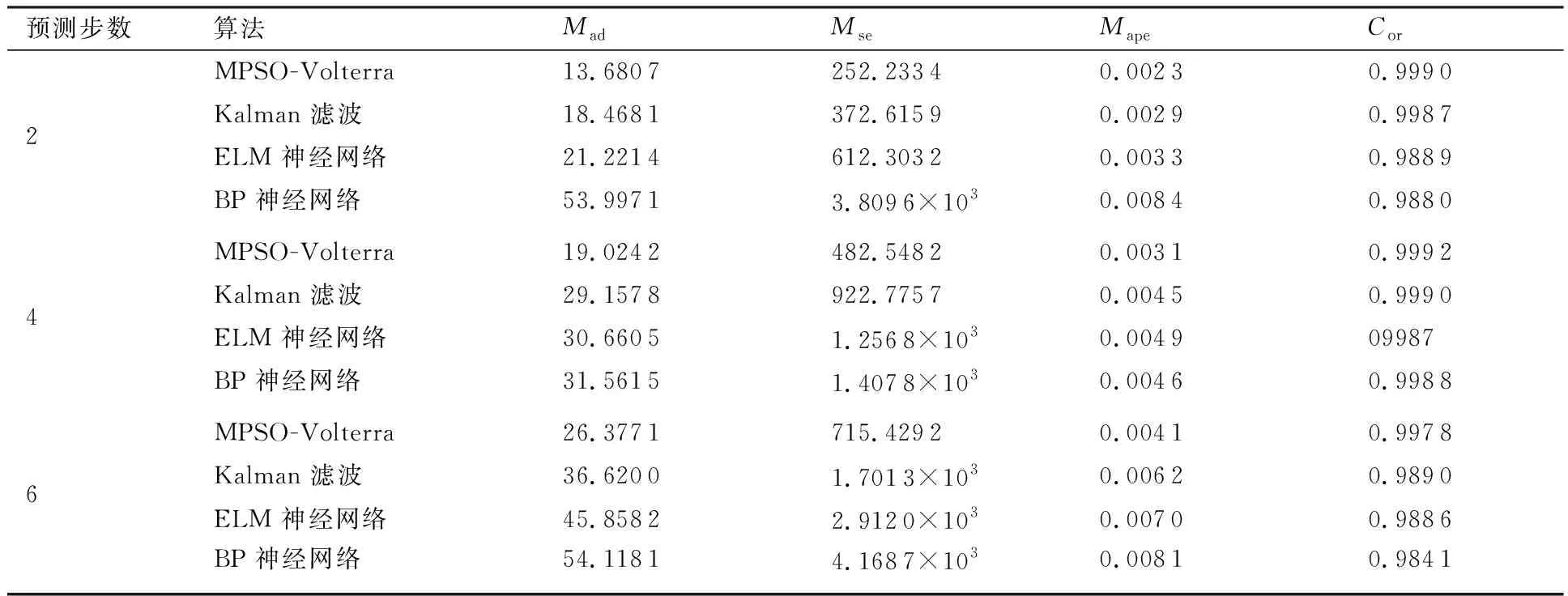
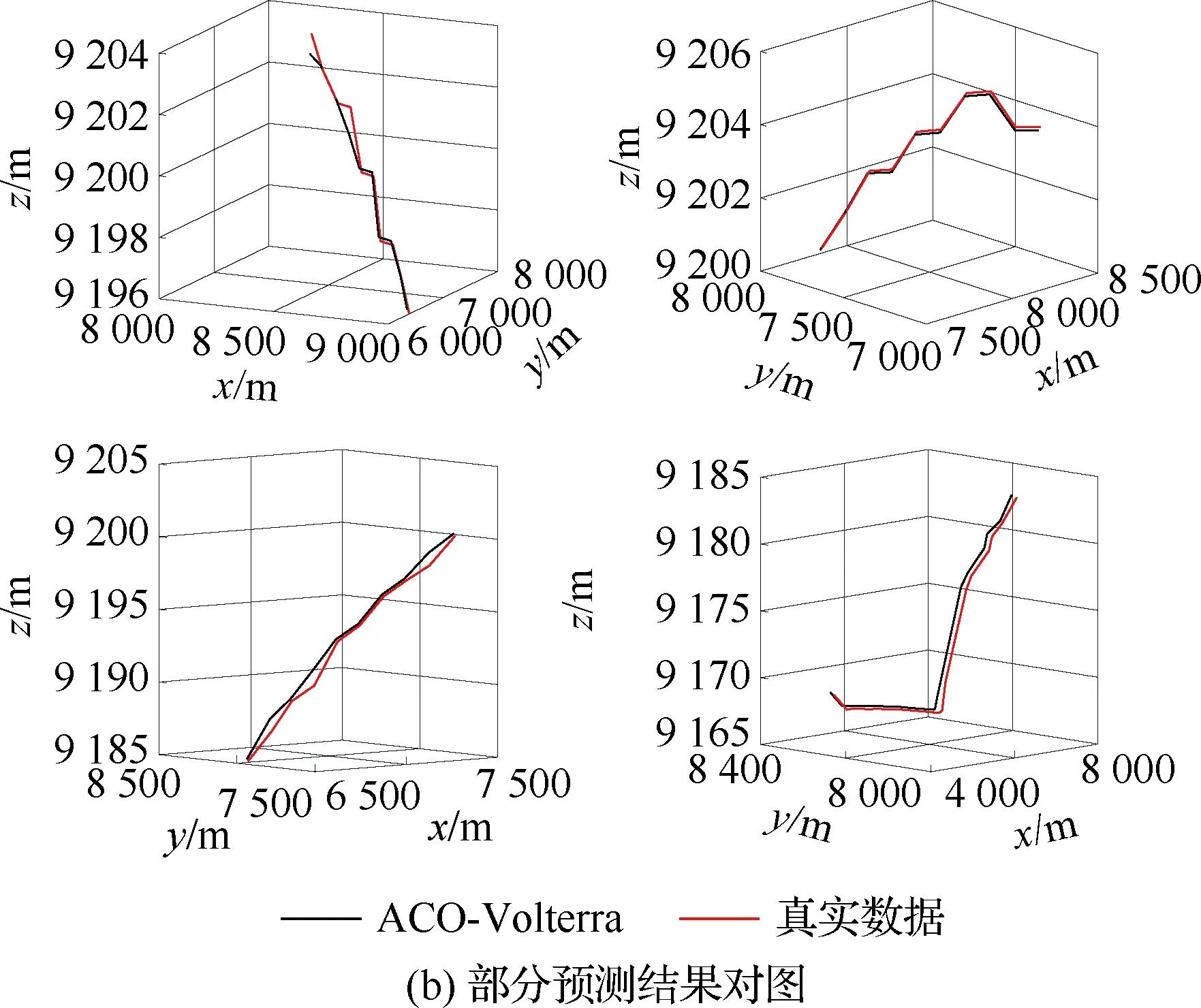
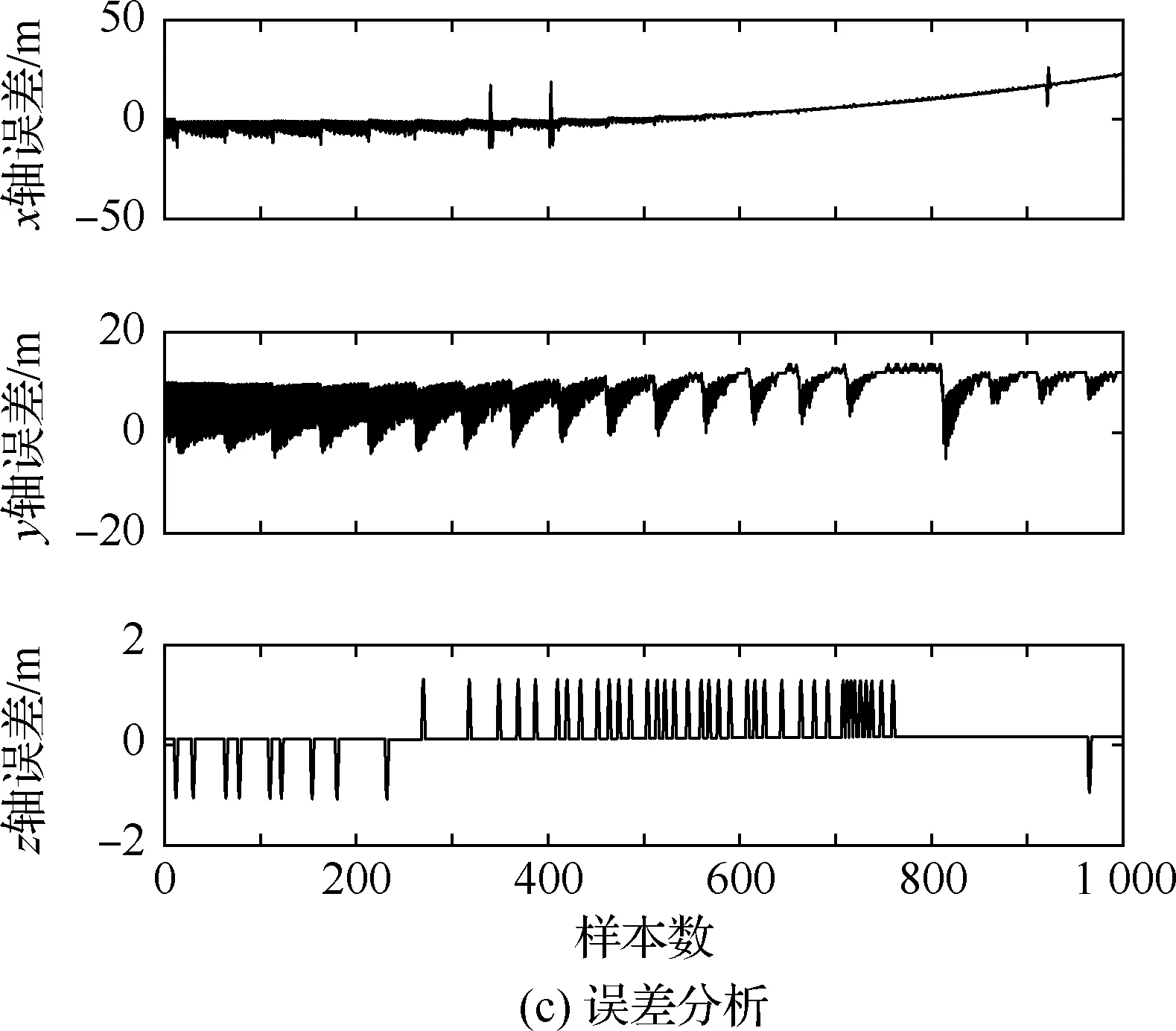
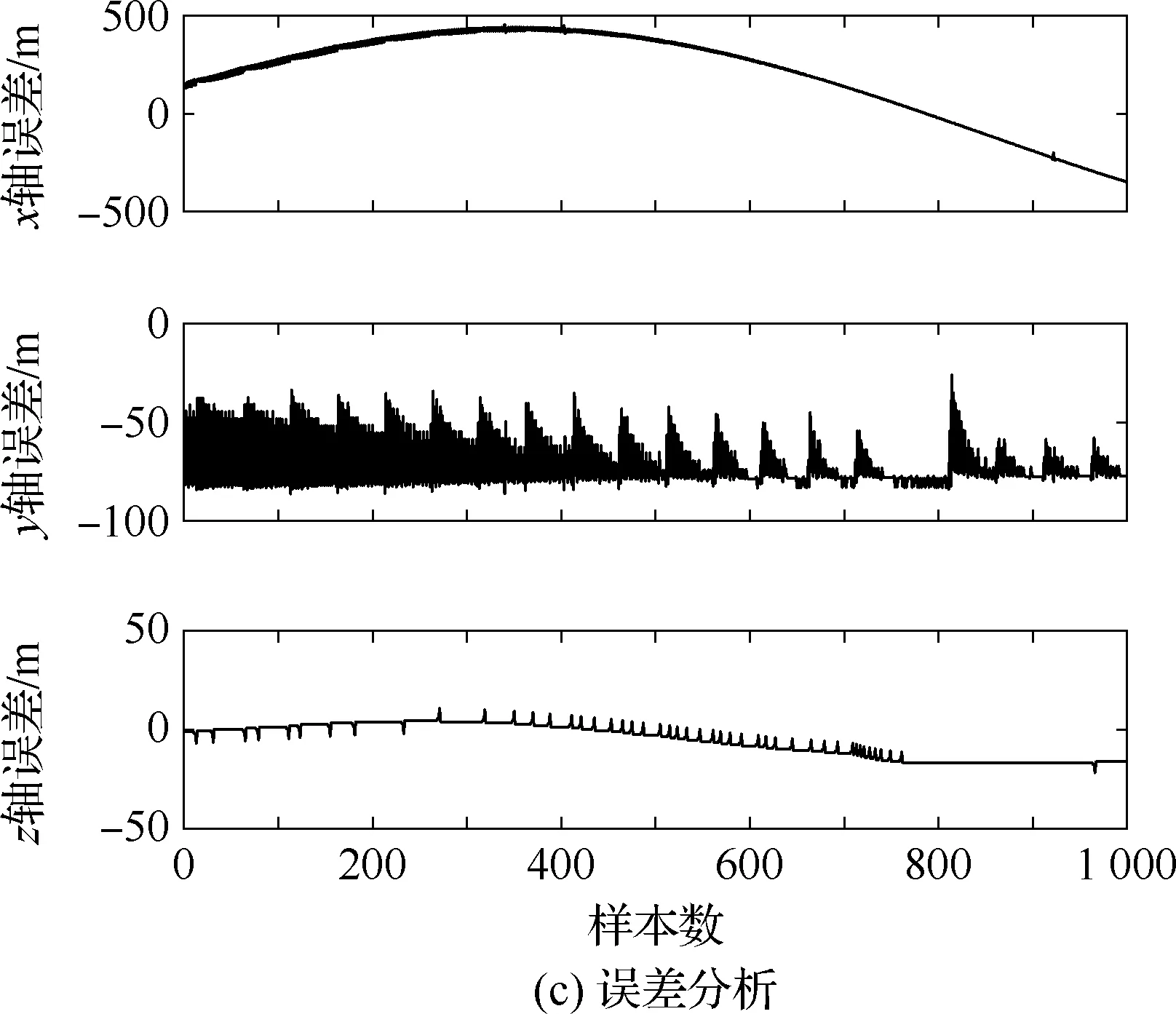
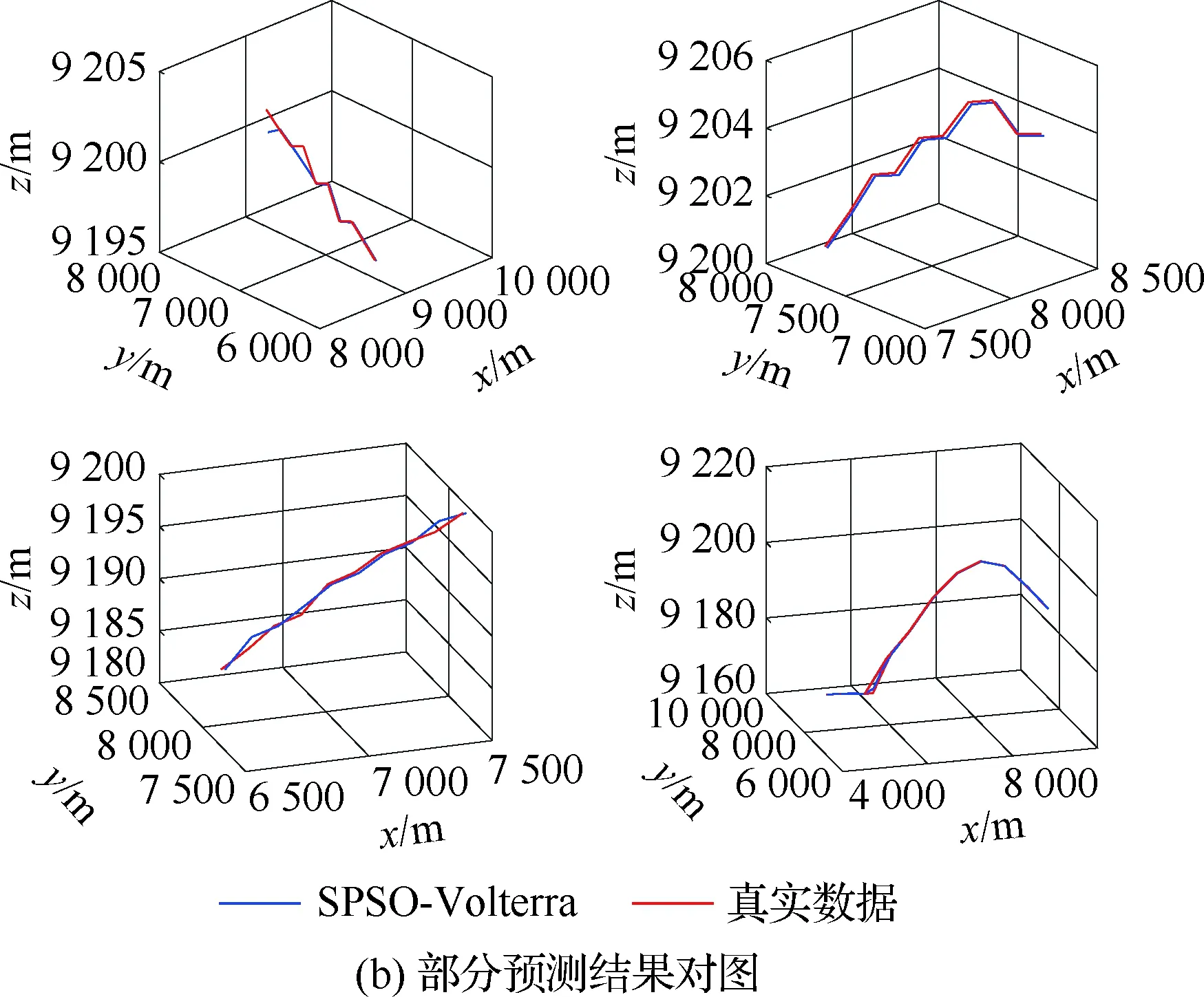
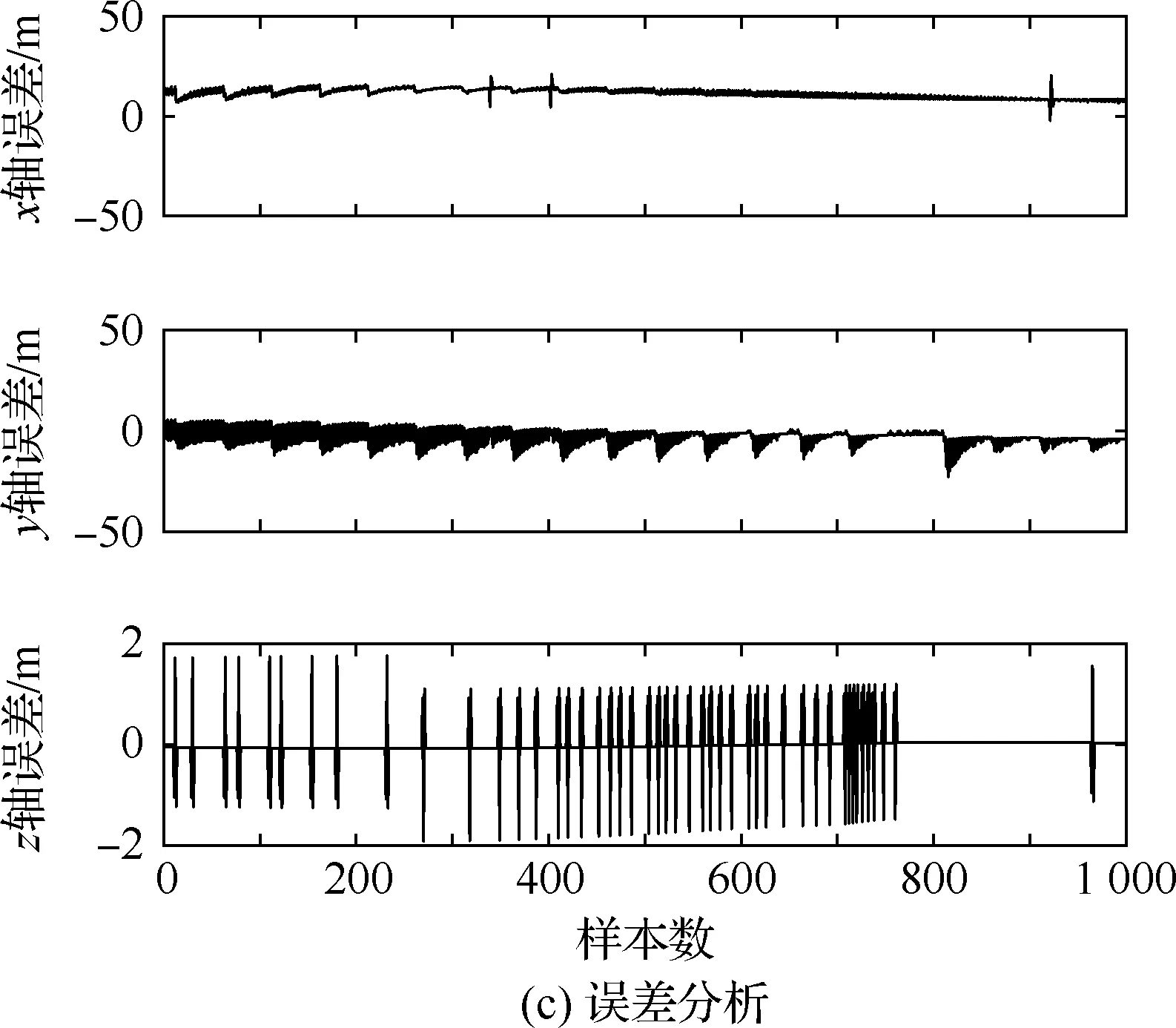
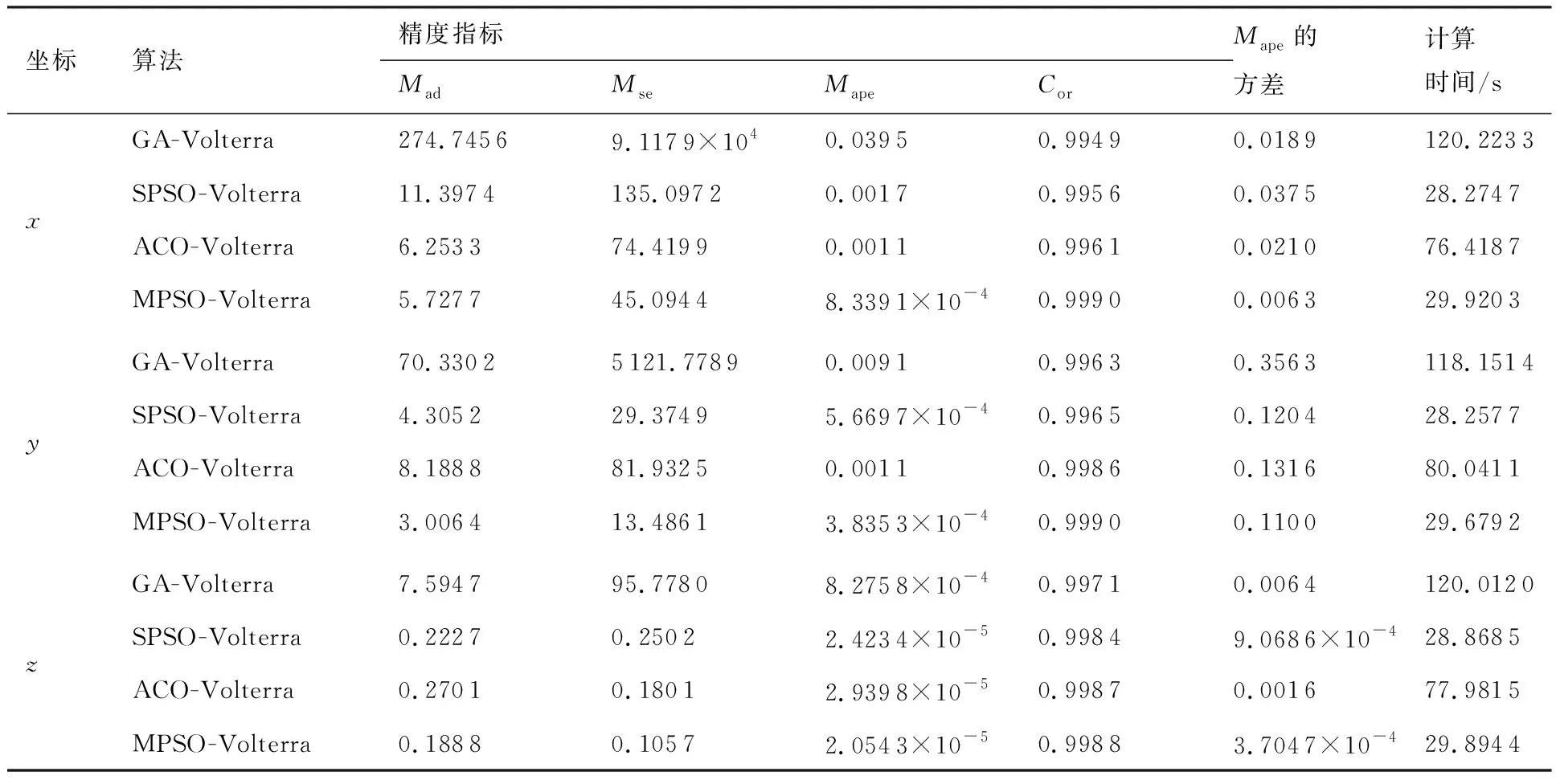
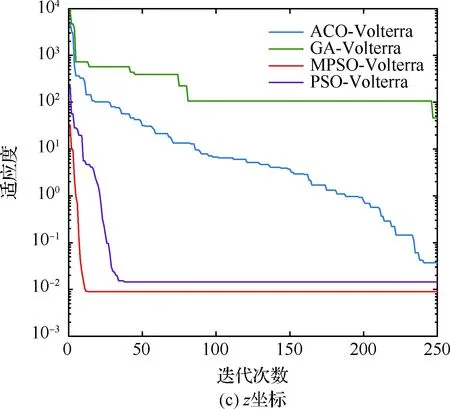
算法1:基于Skew-Tent映射初始化粒子種群設置粒子種群規模為n以及最大混沌迭代步數Kmax1.for i=1 to n do2.for j=1 to D do3.隨機生成一個隨機數φ0,j∈(0,1)4.for k=1 to Kmaxdo5.if 0 3.1.2 子種群劃分 假設X(t)={X1(t),X2(t),…,Xn(t)}為算法第t次迭代時的粒子群,f(Xj(t))為第j個粒子的適應度值,適應度函數值越小則表明粒子的位置越優,根據粒子的適應度值定義一些概念: (30) fbest(X(t))=min{f(Xj(t))|j=1, 2, …,n} (31) Xgood(t)={Xj(t)|f(Xj(t)) j=1, 2, …,q; 1 (32) (33) 式中:favg(X(t))為粒子群平均適應度;fbest(X(t))為粒子群最優適應度;Xgood(t)為粒子群的優秀子種群;favg(Xgood(t))為粒子群優秀子種群的平均適應度。基于式(30)~式(33)定義的新概念,可以構建粒子群的精英子種群和普通子種群 Xelite(t)={Xj(t)|f(Xj(t)) j=1, 2, …,s; 1 (34) Xcommon(t)={Xj(t)|f(Xj(t))>favg(Xgood(t)); j=1, 2, …,p;p=n-s} } (35) 式中:Xelite(t)為精英子種群;Xcommon(t)為普通子種群;s為精英子種群規模;p為普通子種群規模。 3.1.3 自適應慣性權重調整策略 1) 精英子種群自適應慣性權重調整策略 假設ωj(t)為第j個粒子在第t次迭代時的慣性權重。為了說明改進粒子群算法中精英粒子群的ωj(t)調整策略,定義: fworst(Xelite(t))=max{f(Xj(t))| j=1, 2, …,s} (36) Perforj= (37) 式中:fworst(Xelite(t))為精英粒子群最差適應度;Perforj為精英粒子種群的性能指標,其取值范圍為[0,1],精英粒子的適應度越好則性能指標Perforj越大,反之則越小;參數α的取值依據具體問題來確定。 將精英粒子種群性能指標Perforj作為第j個精英粒子在第t次迭代時的慣性權重自適應調整因子,則根據性能指標Perforj確定的自適應慣性權重為 ωj(t)=ωmin+(ω′-ωmin)×(1-Perforj(t)) ωmin<ω′<ωmax (38) 式(38)說明,性能指標Perforj越大的精英粒子,在其附近搜索到全局最優解的概率越大,然而較小的慣性權重可以增強算法的局部搜索能力,因此此時的慣性權重ωj(t)應該取較小值,從而保證算法的局部搜索能力;反之,性能指標Perforj越小,在其附近搜索到全局最優解的概率越小,較大的慣性權重可以增強算法的全局搜索能力,因此此時的慣性權重ωj(t)的取值應該較大,從而保證算法的全局搜索能力。 2) 普通子種群自適應慣性權重調整策略 在改進的粒子群算法中,普通子種群調整為 (39) 式中:t為算法的迭代次數;Tmax為最大的迭代次數。 3.1.4 混沌變異策略 1) 算法的收斂測度 為了更好地反映粒子群所處的狀態,避免因為盲目變異而帶來的大量運算以及對算法收斂速度的影響,本文提出利用粒子群的進化深度系數來定量描述粒子群狀態,從而達到合理進行變異操作以擴大算法搜索空間的目的。 (40) (41) 2) 混沌變異策略 根據算法收斂測度判斷算法是否陷入局部最優解,當算法陷入局部最優值時,采取混沌變異使得其跳出局部極值。混沌變異策略的步驟如下: 步驟1采用Skew-Tent混沌映射模型,基于式(26)生成混沌變量XT。 步驟2基于混沌變量生成粒子的混沌擾動量Xnew,即 (42) 3) 利用混沌變量對粒子進行混沌擾動: (43) 利用改進的粒子群算法對Volterra級數參數進行辨識,在此基礎上,利用辨識之后的Volterra級數模型對目標機動軌跡進行預測,具體流程如圖1所示。 圖1 基于MPSO的Volterra模型辨識算法流程圖Fig.1 Flow chart of identification algorithm of Volterra kernel based on MPSO 通過仿真檢驗本文算法的性能,同時與標準粒子群優化(SPSO)算法、遺傳算法(GA)以及蟻群優化(ACO)算法進行對比。考慮三階Volterra模型: y(k)=1.56x(k)-x(k-1)+0.68x(k-2)+ 0.85x2(k)-2.17x2(k-1)+ 1.39x2(k-2)+1.18x(k-1)x(k-2)+ 1.26x3(k)-0.83x(k)x2(k-1)+ 1.69x(k-1)x2(k-2)+1.41x3(k-2) (44) 式(44)Volterra級數模型中的一~三階核的記憶長度均為3,核系數向量為 H=[1.56, -1.00, 0.68, 0.85, 0, 0, -2.17, 1.39, 1.26, 0, 0, -0.83, 1.69, 0.00, 0, 0, 0, 1.41]T 本文中所使用的仿真軟件為MATLAB 2017a,仿真環境:CPU為Intel Core i7 2.60 GHz,內存為16 GB,操作系統為Microsoft Windows 10。本文所采用算法的初始參數設置如表1所示。為了保證算法性能比較的客觀性,所有仿生智能算法均采用:種群規模N=50;空間維數D為19,即為Volterra級數核系數個數;最大迭代次數Tmax=250。表2為4種算法對Volterra級數模型進行辨識的結果,Rou為信息表的揮發因子。 表1 智能算法參數設置Table 1 Parameter setting of intelligent algorithm 表2 Volterra級數模型辨識結果Table 2 Estimation results of Volterra model 通過表2可以看出,4種辨識Volterra級數模型的算法均可以得到近似于真實值的核系數,說明這4種算法均能夠用于Volterra級數模型的參數辨識,其中本文改進的粒子群算法得到的估計值與真實值更加接近,辨識精度更高。 本文主要對比MPSO-Volterra模型與其他預測模型在預測精度、算法實時性和穩定性方面的性能差異。預測精度采用平均絕對誤差(Mean Absolute Deviation,Mad)、均方誤差(Mean Square Error,Mse)、平均絕對百分比誤差(Mean Absolute Percentage,Mape)和相關系數(Correlation Coefficient,Cor)4個指標來衡量,性能指標定義為 (45) (46) (47) (48) 對于不同的預測算法的運行效率,可以采用在相同的仿真環境下,計算相同的問題所需要的時間來評價;對于模型的穩定性,可以采用在相同的仿真環境下重復性實驗結果的方差來評定。 在三維慣性坐標系中,飛機坐標用三維坐標x、y、z進行表示。傳統的目標機動軌跡預測方法時間目標的三維坐標作為一個整體來預測模型的輸入和輸出,而本文基于對相空間重構理論分析可知,目標的軌跡三維坐標時間序列所呈現出的數據特征不盡相同,故需要將其進行獨立預測。 本文從空戰訓練測量儀(Air Combat Maneuvering Instrument,ACMI)中選取一段時間連續的4 000組數據,將其中前3 000組數據作為預測模型的訓練數據,后1 000組數據作為預測模型的測試數據。為了提高目標機動軌跡三維坐標的預測精度,首先基于相空間重構理論對目標機動軌跡時間序列進行相空間重構。根據C-C法確定目標機動軌跡x方向嵌入維數mx=7和時間延遲τx=9;y方向的時間延遲τy=5,嵌入維數my=8;z方向的嵌入維數mz=8,嵌入維數τz=2。采用單步預測方式,設置預測步數η=1。模型輸入為[T(k),T(k-τ),…,T(k-(m-1)τ) ],且T=X,Y,Z預測模型輸出為T(k+1) 。 4.3.1 目標機動軌跡單步預測效果對比分析 鑒于目前關于目標機動軌跡研究存在兩類方法,即基于卡爾曼濾波算法以及以神經網絡為主的機器學習智能算法,為了對比分析本文所提出的MPSO-Volterra級數預測模型與上述兩種算法的優劣,分別采用本文預測算法與BP神經網絡、ELM神經網絡以及Kalman濾波算法對目標機動軌跡進行預測,通過性能指標來分析基于不同預測機理的預測算法之間存在的差異。 采用4種機理的不同預測算法對目標機動軌跡的三維坐標進行預測,預測結果如圖2~圖5所示,同時為了更加清晰地反映不同機理預測方法的性能差異,故將不同的算法的性能指標記錄在表3中。由于本文采取的是中遠距對抗數據樣本,導致數據量級較大,同時本文預測算法誤差較小,與真實數據之間的量級差異導致在預測結果對比圖中,不能清晰看出預測值與真實值之間的差異,故各選取了4段區域預測情況進行局部預測效果呈現。 圖2 MPSO-Volterra模型預測結果對比Fig.2 Comparison of prediction results of MPSO-Volterra model 首先,通過觀察圖2~圖5中基于不同機理的預測算法對目標機動軌跡三維坐標進行預測的結果,可以看出,無論是基于卡爾曼濾波算法,還是基于神經網絡,抑或是基于仿生智能算法辨識的Volterra級數預測算法,在對目標機動軌跡三維坐標進行預測時,其誤差都是比較小的,這就說明基于3種機理的預測算法適用于目標機動軌跡預測問題。其次,通過表3中預測性能指標可以看出,基于仿生算法辨識的Volterra級數預測模型的性能更佳,而基于卡爾曼濾波算法和ELM神經網絡的預測算法的性能較MPSO-Volterra級數預測模型差一點,說明MPSO-Volterra級數預測模型在目標機動軌跡預測方面更具有優勢。 圖3 Kalman濾波模型預測結果對比Fig.3 Comparison of prediction results of Kalman fillter model 圖4 ELM神經網絡模型預測結果對比Fig.4 Comparison of prediction results of ELM neural network model 圖5 BP神經網絡模型預測結果對比Fig.5 Comparison of prediction results of BP neural network model 從機理上分析可知,MPSO-Volterra級數預測模型本質上是利用目標機動軌跡時間序列的混沌特性,通過擬合訓練混沌吸引子軌道來預測非線性系統,通過線性三階Volterra級數的乘積耦合方式來實現,因此可同時避免因級數階數較大而導致核函數求解困難和大量存在非線性耦合對Volterra級數核系數不收斂或不穩定的影響,提高了預測精度。另一方面,Volterra級數利用線性自適應算法調整模型參數,這種動態性可以提高其利用新數據預測的適應性和準確性。但是也存在一定的不足,采取仿生算法辨識Volterra級數預測模型計算時間較長,這是因為,算法的復雜度高于其他預測算法,自然預測模型的運行時間多余其他預測算法,根據NFL(No Free Lunch)理論可知,任何一個算法不可能全面優于其他算法,但是存在的這一點不足也是后續著重研究的算法,盡可能提高算法的實時性。 4.3.2 目標機動軌跡多步預測結果對比分析 表4 4種目標x方向坐標多步預測模型性能比較Table 4 Performance comparison of target x-coordinate multi-step prediction of four different prediction methods 表5 4種目標y方向坐標多步預測模型性能比較Table 5 Performance comparison of target y-coordinate multi-step prediction of four different prediction methods 表6 4種目標z方向坐標多步預測模型性能比較Table 6 Performance comparison of target z-coordinate multi-step prediction of four different prediction methods 通過表4~表6中在不同預測步數下各個預測算法的性能指標數值可以看出,本文提出的MPSO-Volterra級數預測模型的性能更佳,Kalman濾波算法、ELM神經網絡以及BP神經網絡的預測性能在不同方向坐標預測中表現出不同的性能差異較大,這些都說明本文所提出的MPSO-Volterra級數預測模型更加適用于目標軌跡預測問題。從機理上分析各種算法表現出不同的預測性能的原因: 1) BP神經網絡是一種單隱含層前饋神經網絡,其可以通過樣本數據不斷地訓練學習擬合任何輸入、輸出之間的各種復雜的非線性關系,具有一定的魯棒性和泛化能力,但是BP神經網絡算法自身也存在一定的“缺陷”,由于BP神經網絡算法在學習的過程中采用標準梯度下降算法,在采用樣本對其進行訓練時,易陷入局部極值,導致樣本學習失敗;同時,BP神經網絡算法也存在學習“過擬合”的現象,一般情況下,BP神經網絡的預測能力與樣本訓練能力呈正相關,但是實際上隨著樣本訓練能力的提高,BP神經網絡預測能力會達到一個極限值,隨后會出現預測能力下降的現象,故BP神經網絡在預測過程中存在一些自身無法克服的不足,因而預測性能也會有所影響。 2) ELM神經網絡與傳統的神經網絡算法相比,ELM神經網絡具有相對明顯的優勢,但同時也存在一定的固有缺陷:一方面,網絡的輸入層與隱含層之間的權值、閾值進行隨機確定,因而具有一定的盲目性,從而導致ELM網絡的穩定性變差;另一方面,如果訓練數據中存在噪聲或離群點,容易導致網絡的隱含層輸出矩陣呈現出病態的問題,使ELM神經網絡的魯棒性變差、泛化性能降低。在復雜的電磁環境下,基于機載傳感器獲取的目標機動軌跡,很容易出現一些離群點,從而導致ELM神經網絡預測性能下降。 3) Kalman濾波算法采用不斷“預測-修正”的遞推方式進行,先進行預測,再根據觀測值得到的新息和卡爾曼增益對預測值進行修正。卡爾曼濾波通過迭代來消除估計誤差,但誤差具有傳遞性,隨著迭代次數的增加,目標運動狀態估計的精度也會隨之下降。同時,新息反映了預測值偏離觀測值的程度,當目標的運動狀態發生突變或者目標運動模型不夠準確時,目標下一時刻的運動狀態預測精度降低,空戰中目標的運動模式是不斷變化的,很容易導致算法預測精度下降;由于卡爾曼濾波預測算法需要實時更新新息來修正預測誤差,在進行多步預測時,目標的實時新息得不到更新,算法的預測精度也會隨之下降,在空戰中目標的信息獲取并不是可以實時準確獲得的,因Kalman濾波算法在空戰中進行多步預測存在不足。 4) Volterra自適應濾波器預測模型在預測過程中僅需很少的數據樣本就可對混沌時間序列進行預測,而且可自動追蹤混沌運動軌跡,該預測模型的預測精度較高。 4.4.1 機動軌跡時間序列預測效果對比 本節將本文提出的基于改進粒子群優化的Volterra級數預測模型與GA算法優化的Volterra級數預測模型、ACO算法優化的Volterra級數預測模型以及SPSO算法優化的Volterra級數預測模型對目標機動軌跡時間序列單步預測結果進行對比,預測結果對比如圖2、圖6~圖8所示。 圖2、圖6~圖8代表了4種智能算法辨識的Volterra級數預測模型對目標機動軌跡預測的結果對比曲線和誤差曲線。從圖中可以看出,在采用4種智能算法辨識的Volterra級數預測模型對目標機動軌跡的三維坐標進行預測時,各個點的誤差均在零點附近較小范圍內波動,說明4種智能算法對Volterra級數辨識的有效性,說明群智能優化算法能夠有效解決Volterra級數核函數求解困難的問題,同時也說明了Volterra級數具有優良的非線性擬合和預測能力;同時也存在一些將來需要解決的問題,如何選擇優化算法以及怎樣改進優化算法的問題,本文僅僅初步探索,利用群智能優化算法辨識Volterra級數,并將辨識之后的Volterra級數模型用于預測問題。 圖6 ACO-Volterra模型預測結果對比Fig.6 Comparison of prediction results of ACO-Volterra model 圖7 GA-Volterra模型預測結果對比Fig.7 Comparison of prediction results of GA-Volterra model 圖8 SPSO-Volterra模型預測結果對比Fig.8 Comparison of prediction results of SPSO-Volterra model 為了對比分析不同優化算法辨識的Volterra級數預測模型在預測精度、速度和穩定性上的不同,在相同的仿真條件下,分別采用SPSO-Volterra、GA-Volterra和ACO-Volterra模型對目標機動軌跡時間序列進行單步預測。每一種預測模型獨立重復運行50次,統計得到模型預測結果的平均絕對誤差、均方誤差、平均絕對百分比誤差、線性相關度以及算法的平均運行時間。其中,平均絕對百分比誤差是反映預測值和真實值之間偏離程度的重要指標,預測模型的穩定性采用Mape的方差來評價。表7給出了不同的預測模型對目標機動軌跡時間序列進行預測時所呈現的性能。 從表7可以看出,與其他優化算法辨識之后的Volterra級數預測模型相比較,在預測精度方面,MPSO-Volterra預測模型的Mad,Mse以及Mape的值均是最小,Cor最高,這些可以說明MPSO-Volterra預測模型在目標機動軌跡時間序列的預測精度上具有明顯的優勢。在預測穩定性方面,MPSO-Volterra預測模型的平均絕對百分比誤差Mape的方差最小,這說明MPSO-Volterra預測模型的穩定性最好。在算法的運行速度方面,MPSO-Volterra預測模型和SPSO-Volterra預測模型所需要的計算時間遠少于ACO-Volterra預測模型和GA-Volterra預測模型,由于MPSO-Volterra預測模型中執行了自適應參數調整機制和混沌變異機制,導致其運行時間略多于SPSO-Volterra預測模型。綜合來看,在目標機動軌跡時間序列預測中,MPSO-Volterra預測模型相較于其他預測模型,在預測精度、速度以及穩定性方面均具有模型優勢。 4.4.2 不同算法優化性能對比 對目標機動軌跡的三維坐標分別進行建模與預測時,PSO-Volterra算法、GA-Volterra算法和ACO-Volterra算法以及本文所提MSPO-Volterra算法的收斂曲線對比結果見圖9。橫坐標為算法迭代次數,縱坐標為算法的適應度函數的適應值。 在圖9(a)中,x坐標下ACO-Volterra、GA-Volterra、PSO-Volterra和MSPO-Volterra算法的適應度函數值達到穩定時的迭代次數分別是217、170、81、139;在圖9(b)中,y坐標下4種算法的適應度函數值達到穩定時的迭代次數分別是241、81、15、91;在圖9(c)中,z坐標下4種算法的適應度函數值達到穩定時的迭代次數分別是226、80、22,48。因為是將Volterra級數的預測誤差設定為智能優化算法的適應度函數,適應度函數值越大,則Volterra級數預測誤差越大,通過上述分析可見,對比與現有的智能算法辨識Volterra級數模型,本文所提出的MPSO-Volterra級數算法模型不僅具有較高的收斂精度,同時還具有較快的收斂速度。 表7 各種算法對目標三維坐標的預測性能指標Table 7 Prediction performance indexes of various algorithms for target 3D coordinates 圖9 適應度函數值比較Fig.9 Comparison of fitness function values 從機理上分析可知,粒子群算法是一種基于種群模擬的群體仿生智能優化算法,具有運行時間短、容易收斂以及魯棒性強的優點,然而非線性系統Volterra級數核函數辨識實際上是一個高維度優化問題,PSO算法在面對優化高維度問題時,容易出現早熟現象,導致算法陷入局部最優而無法跳出,同時還存在收斂精度不高的問題。GA算法在用于參數辨識時,存在一些自身無法克服的問題,即優化時間長且容易陷入局部最優。由于ACO算法中的多個個體的運動是隨機的,隨著蟻群種群的增大,尋找到一條較優的路徑需要更多的時間,此外,ACO算法中融入了正反饋機制,如果正反饋過于強,容易使得算法陷入局部最優,反饋過弱,則使得算法收斂速度減慢。針對上述機理分析,GA、PSO以及ACO算法在參數辨識問題或者高維度優化問題上都存在一定的不足,本文所采取自適應策略和混沌變異策略可以有效提高基本粒子群算法在高維度問題優化方面所呈現出的不足。 本文對目標機動軌跡時間序列進行了相空間重構,同時對其進行了混沌特性的判定識別。引入基于改進粒子群算法辨識的Volterra泛函級數模型,建立一種基于Volterra級數的目標機動軌跡預測模型。 1) 本文采用0-1檢測法對目標機動軌跡時間序列進行了混沌判定。結果表明:實際記錄的目標機動軌跡存在混沌現象,實際記錄的目標機動軌跡時間序列為混沌時間序列。0-1檢測法可以較準確地判斷時間序列中是否含有混沌特性,從而為時間序列的分析與預測提供前提。 2) 由于已確定目標機動軌跡存在混沌現象,本文引入非線性Volterra模型,結合智能優化算法,建立了基于改進粒子群算法辨識的Volterra自適應預測模型。該預測模型綜合利用線性和非線性因素,充分利用了目標機動軌跡的混沌特性,更符合混沌序列的非線性本質。實驗結果表明,三階Volterra自適應預測模型能夠很好地對目標機動軌跡做出預測,且預測精度較高。 3) 本文將改進的粒子群算法與非線性Volterra泛函級數模型相結合,同時在仿真中,將該預測方法與Kalman濾波算法以及機器學習算法的預測性能進行了對比分析。實驗結果表明,本文提出的算法在單步和多步預測方面的性能都較好,可以適用于目標機動軌跡預測問題。 4) 本文將改進的粒子群算法與非線性Volterra泛函級數模型相結合,同時在仿真中,將該預測算法與SPSO-Volterra模型、ACO-Volterra模型和GA-Volterra模型的預測性能進行了對比分析。實驗結果表明,本文提出的算法預測精度高,且算法的收斂速度快。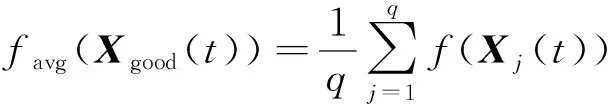
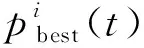
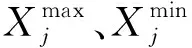

3.2 Volterra級數目標機動軌跡預測流程

4 仿真驗證
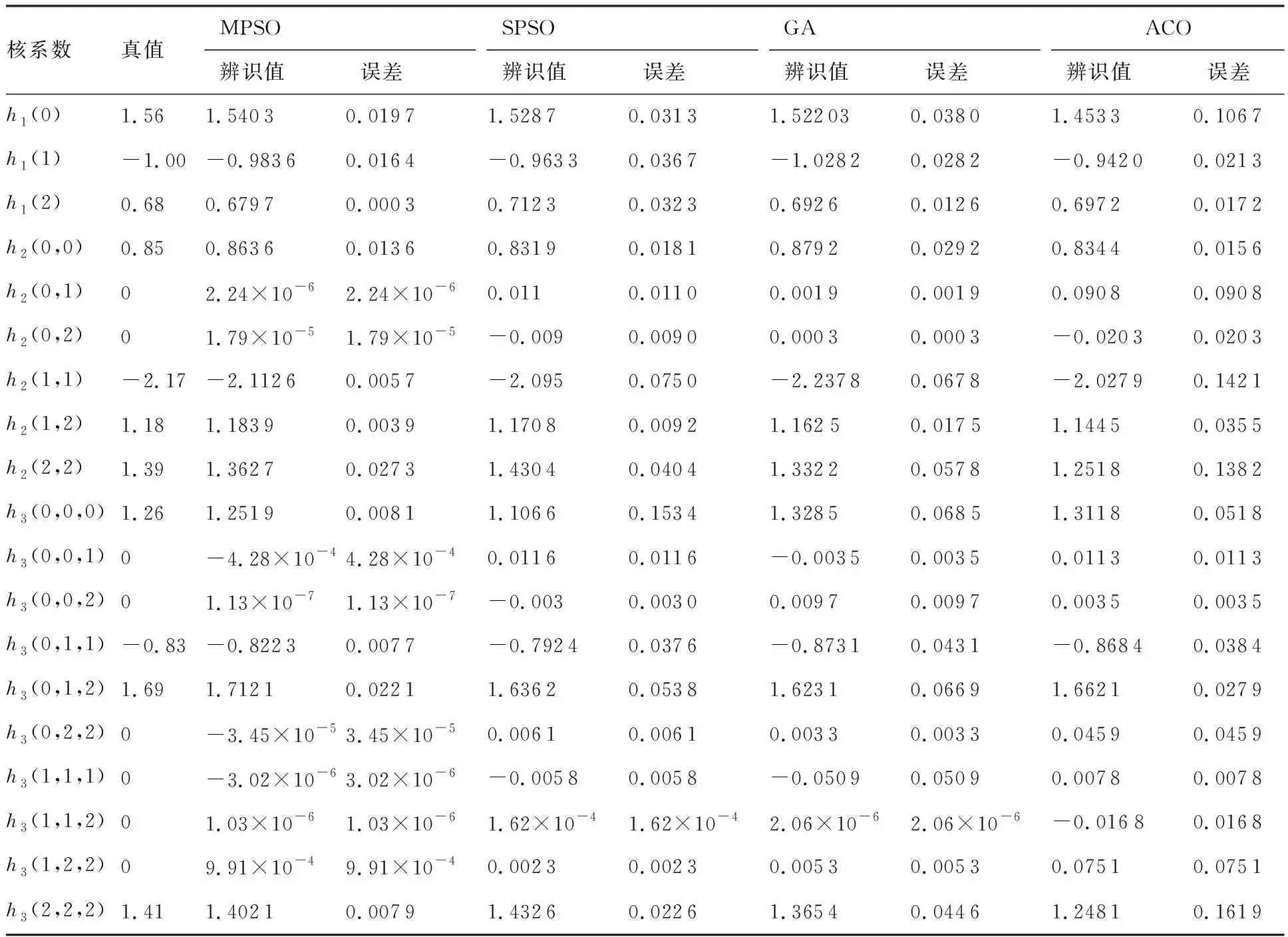
4.1 Volterra級數模型辨識測試

4.2 預測算法性能評價
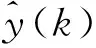
4.3 不同模型單步及多步預測性能對比與分析
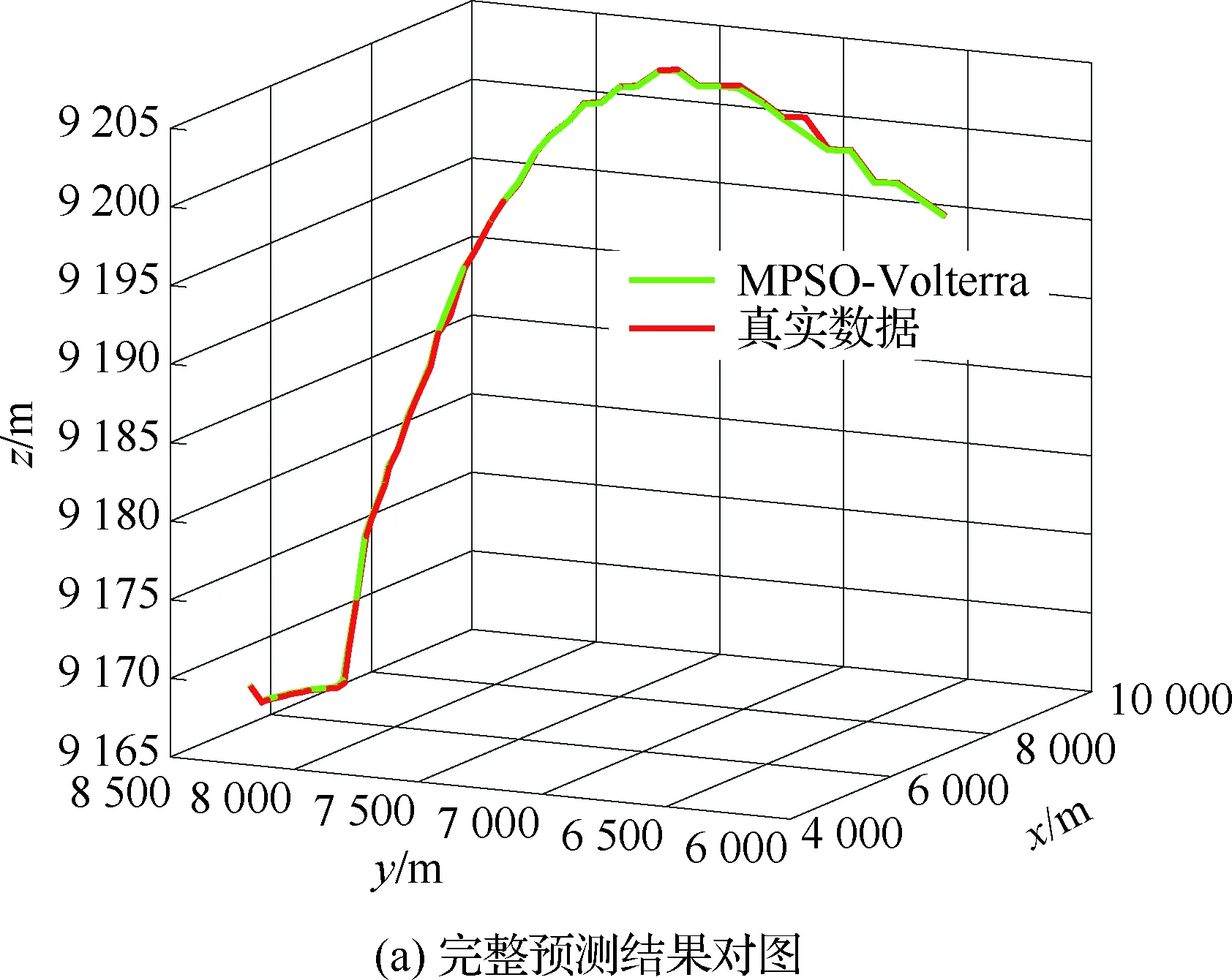
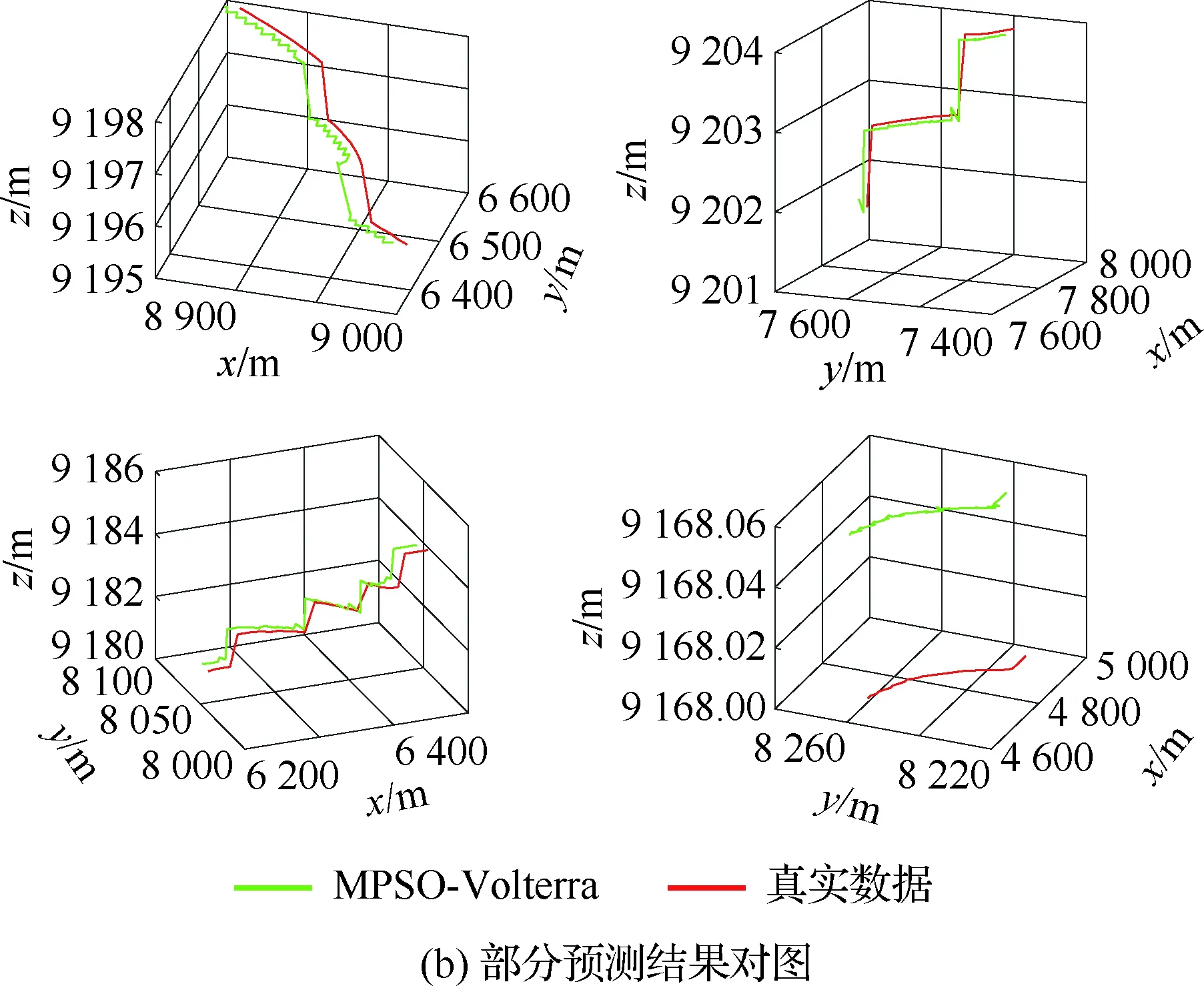
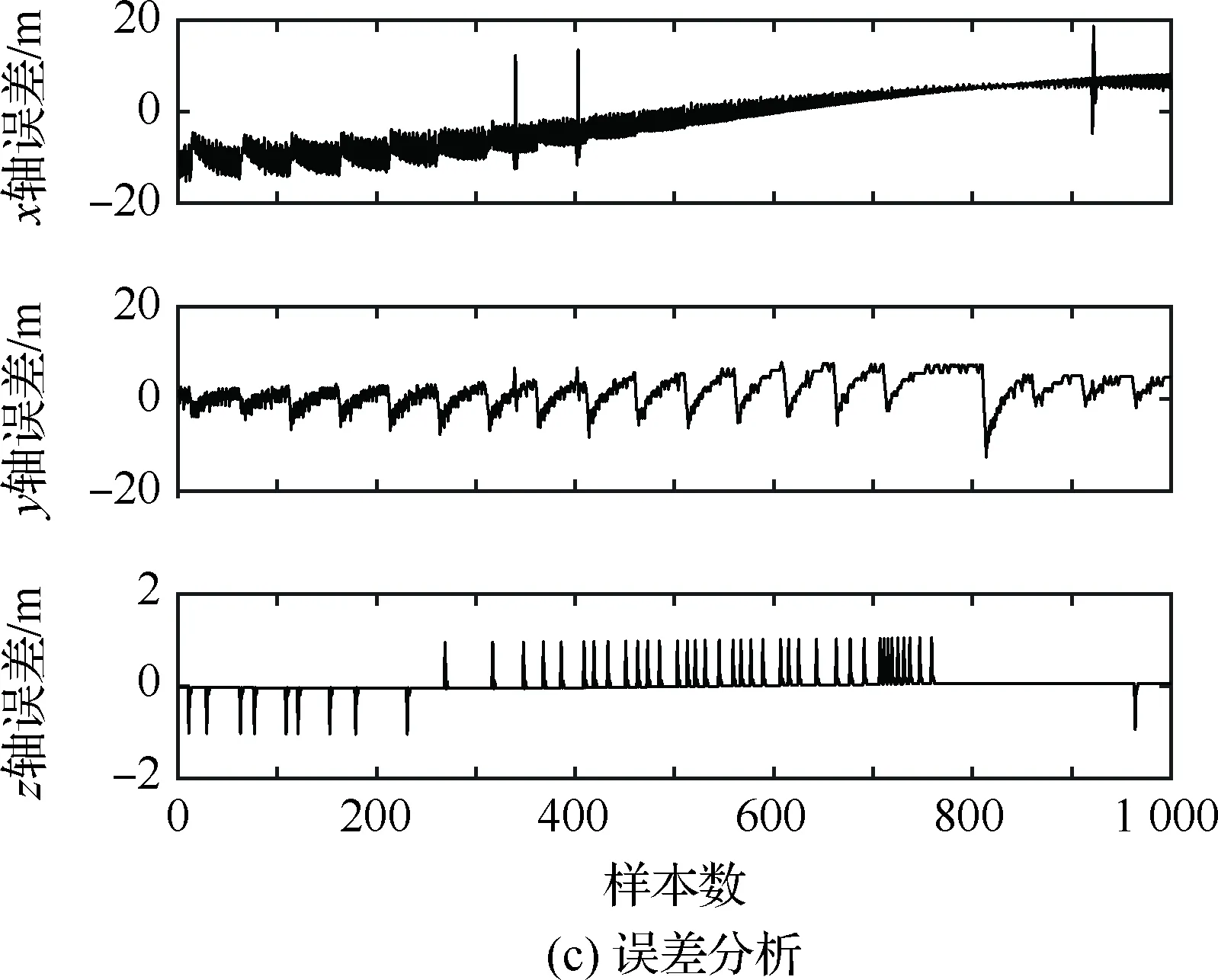
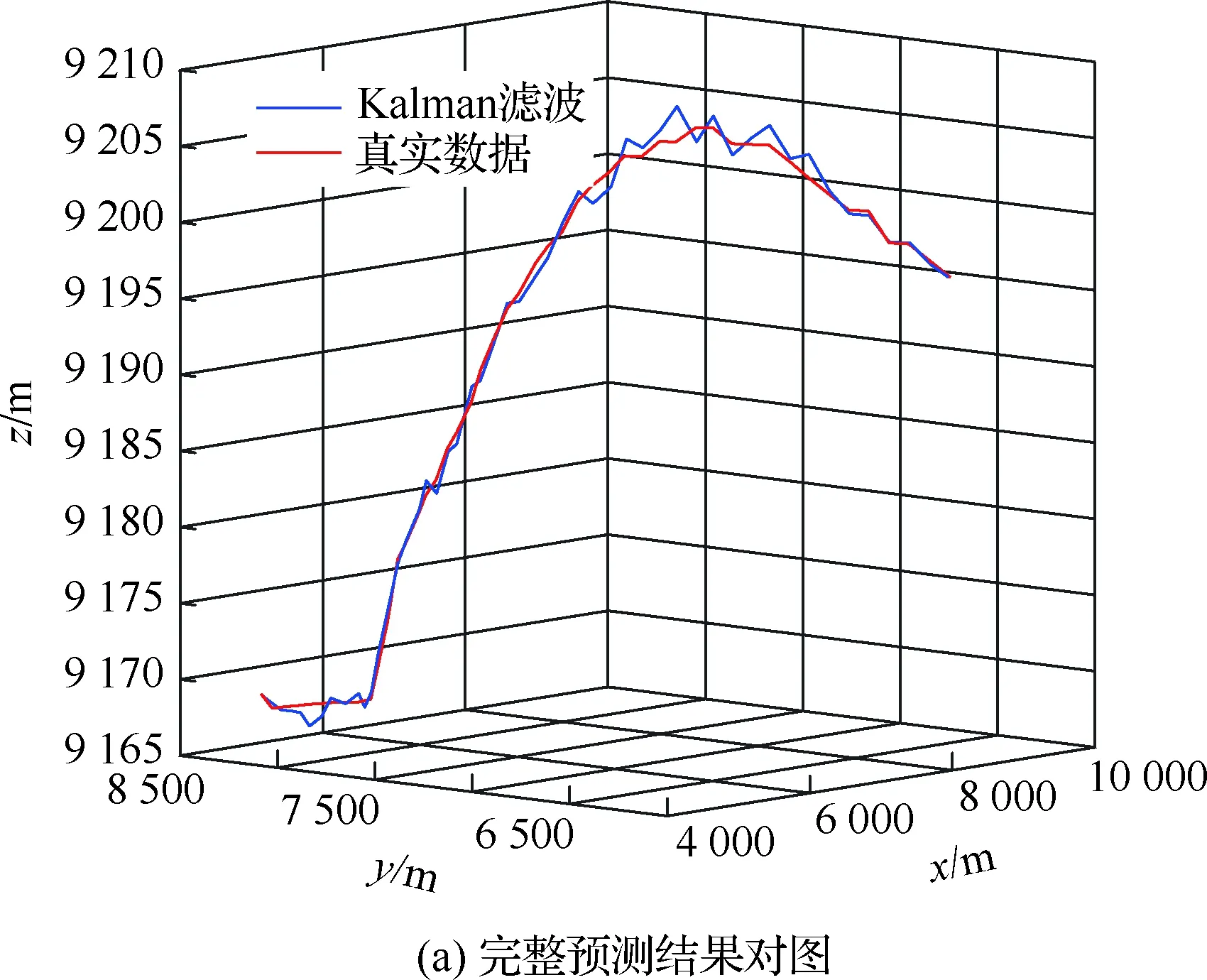
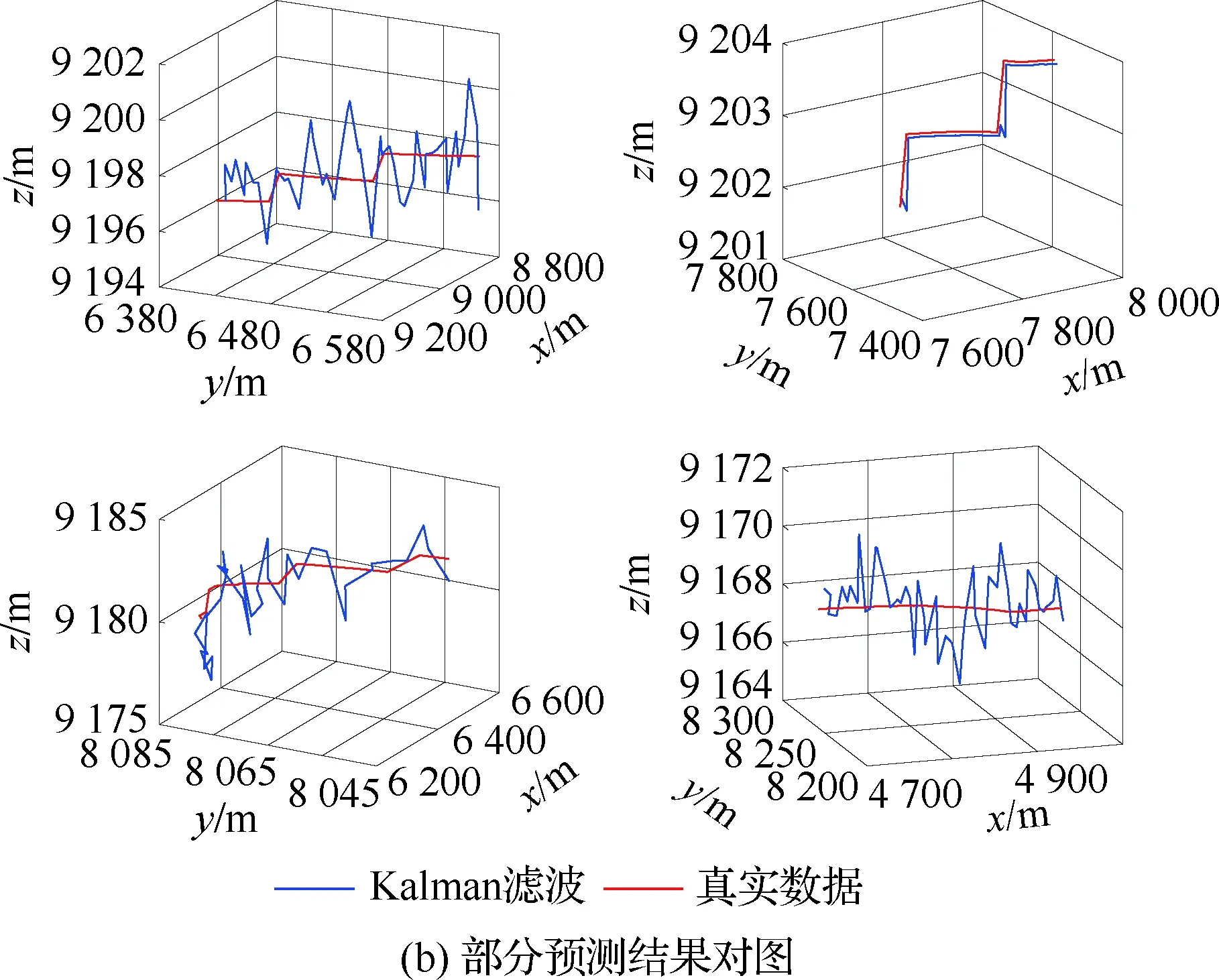
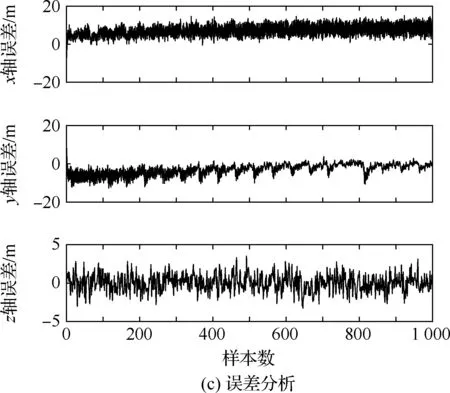
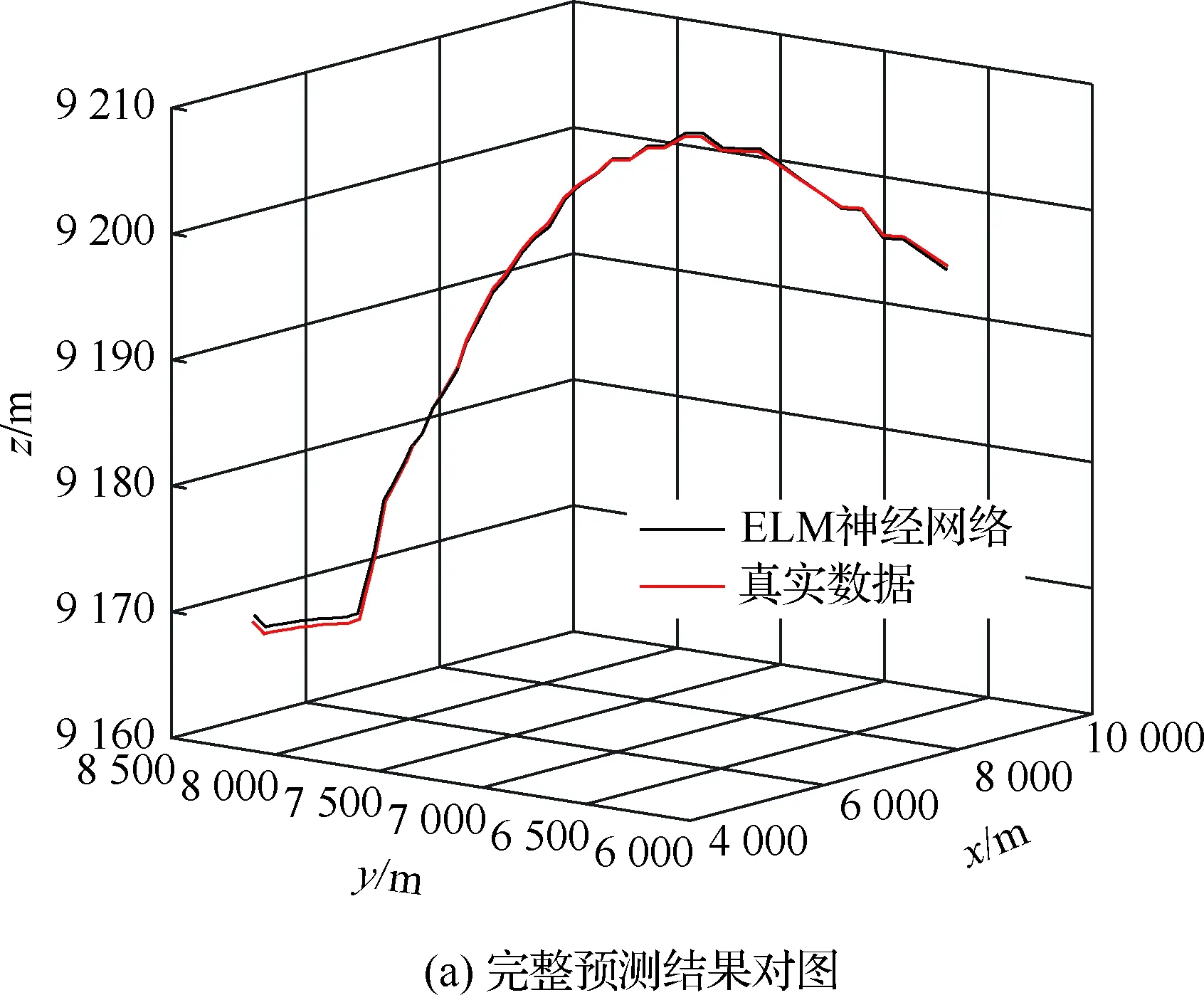
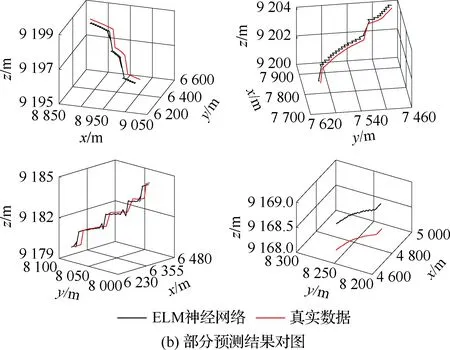


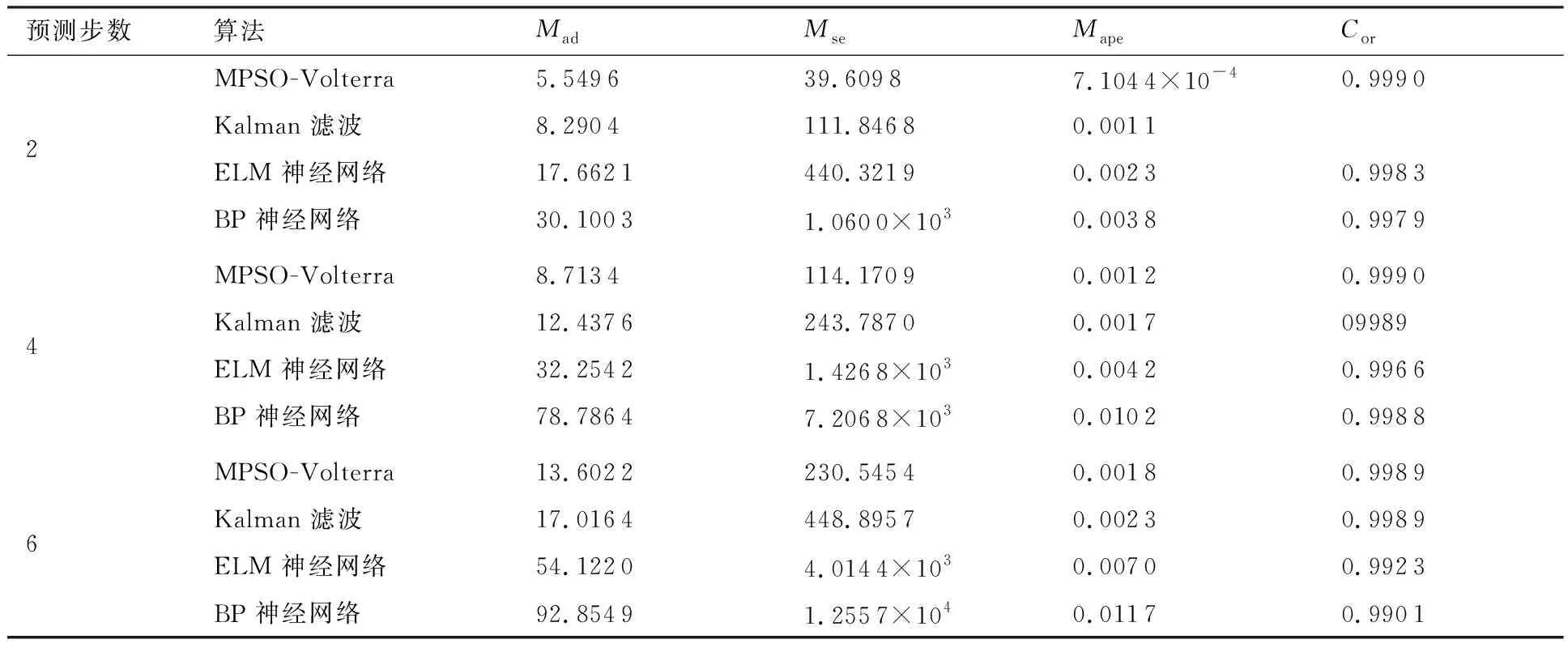
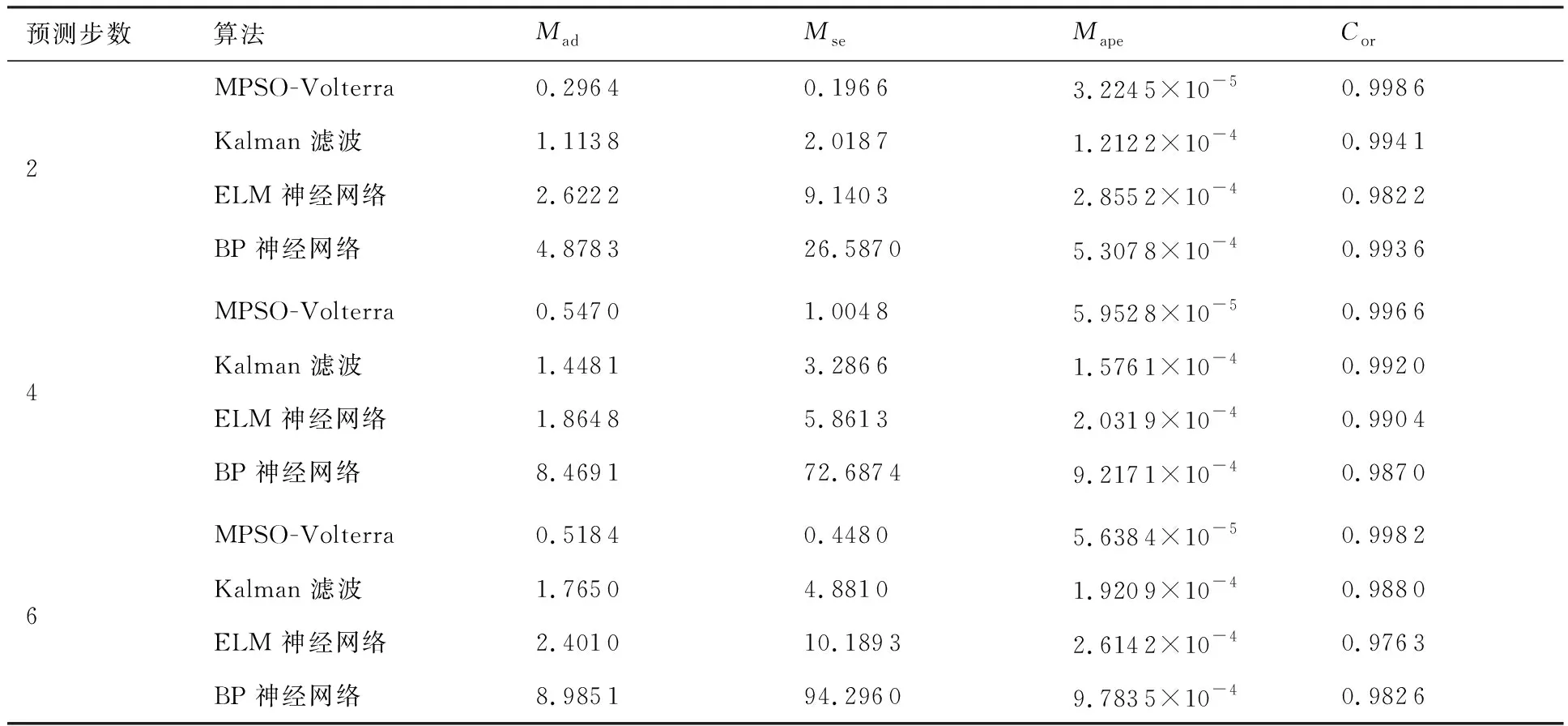
4.4 不同優化算法性能對比




5 結 論

