資源受限下的網絡安全動態博弈模型
鄂小松, 石峻松
(1.樹蛙信息科技(南京)有限公司,江蘇 南京 210033)(2.南京信奧弢電子科技有限公司,江蘇 南京 210039)
一般情況下,網絡中攻防雙方的對抗過程符合博弈論各項特征,因而可將博弈論引入解決攻防雙方策略抉擇問題。在實際對抗中,由于攻防雙方知之甚少,因此在網絡攻防沖突時會產生不完全信息問題。為有效解決不完全信息下的博弈問題,國內外學者進行了大量研究。Harsanyi[1]提出用貝葉斯納什均衡解來解決靜態博弈論中不完全信息問題。針對動態博弈論領域,通常的解決方法包括完美貝葉斯均衡[2]和序貫均衡[3]兩種方法。對于有限動態不完全博弈過程,序貫均衡總能得到混合策略,然而對于完美貝葉斯均衡方法,其計算過程較為復雜。Nayyar等[4]在假設動態隨機非零和博弈狀態和觀測方程是線性的且初始隨機變量為高斯隨機變量的前提下,利用求解線性方程組序列,提出了公共信息馬爾科夫完美均衡計算方法。該方法的關鍵是將初始不完全信息下的博弈過程轉化為一個完全信息下的虛擬博弈過程以及眾多不同的或者更大的狀態/動作空間。然而該方法無法對攻擊者的策略集和效用函數進行差異性分析,且建模過程復雜。此外,為提高隨機博弈過程狀態觀測及動作策略選取效率,Cole等[5]將具有懲罰函數的第三方觀察者引入系統,且為每一個對抗參與者賦予私有信息觀測狀態。模型中每個參與者狀態置信度僅依賴于當前狀態而不依賴其策略,這種假設使得每個參與者當前策略選取受過去私有觀測狀態影響,嚴重時,策略選取將會產生較大偏差。
國內也有不少學者將博弈論引入網絡信息安全領域。劉榮等[6]將信息安全中攻防沖突雙方的收益進行量化,建立了對抗雙方的博弈矩陣,同時將演化博弈理論引入沖突模型,求解攻防雙方對抗過程中網絡動態微分方程。在MATLAB中對網絡攻防雙方對抗過程進行了策略穩定性分析,通過5組均衡解驗證了模型的準確性與有效性,然而在建模過程中假設攻防雙方處于理想化背景,導致在計算對抗雙方博弈沖突過程時,缺乏一定的現實基礎。朱建明等[7]結合網絡對抗攻防雙方效能函數,基于系統動力學方程建立了不完全信息下具有自主學習機制的網絡對抗演化博弈模型,并對模型進行了仿真,驗證了引入第三方動態懲罰策略的非合作演化博弈過程納什均衡的存在性與唯一性,然而建立模型過程中沒有考慮計算資源受限情況。
綜上,為了解決獲取信息不完全以及計算資源受限情況下的網絡安全問題,本文通過量化信息獲取機制及資源受限條件,建立了網絡安全中攻防雙方動態博弈過程方程,并給出了納什均衡及代價函數的計算過程。
1 博弈模型分析與建立
(1)
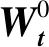
(2)
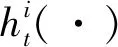
1.1 信息及策略選取模型
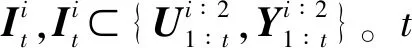
控制器的控制策略可表示為gi,定義為:
(3)

1.2 控制器資源限制模型
在博弈過程中,每一個控制器的可利用資源數量都具有一定限制,控制器i在t時執行的動作及策略選擇不僅依賴于其他控制器的觀測和響應動作,還需考慮自身資源消耗情況。
令控制器集合為J,t時公共信息的增量為Zt,有Zt=Ct/Ct-1。其中,Zt為增量集合, 則Zt={Z1,…,ZT}。因此,控制器i的資源限制條件可表達如下:
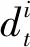
1.3 代價函數及納什均衡
假定每一個控制器都存在一個代價函數,策略固定情況下,所有控制器的總代價函數可表達為:
(4)
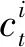

2 博弈模型計算過程
2.1 基本假設
為簡化計算過程,對模型部分條件作如下假設:
假設1:假定系統中各個控制器獲取的公共及私有信息隨時間演化過程如下。
1)獲取的公共信息Ct隨著時間不斷增加,即?t∈T,Ct?Ct+1。令Zt+1=Ct+1/Ct為t到(t+1)時刻公共信息的增量,則Ct+1={Ct,Zt+1}。因此有:
(5)

2)私有信息的演化過程可表達為:
(6)
式(5)表明,t到(t+1)時刻,增加的新公共信息一部分為t時刻選取的動作以及(t+1)時刻的觀測集,另一部分為t時刻部分私有信息。式(6)表明控制器1和2私有信息的演化過程受到不同觀察者及動作的影響。
在公共信息條件已知的條件下,任意時間t,控制器狀態及私有信息的置信度的條件概率模型為:
(7)

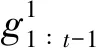
(8)
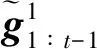
2.2 模型求解
根據假設2可知,Πt僅依賴于公共信息Ct,且由于任意參與者都能得到公共信息,因此對于所有參與者而言,Πt為已知的。因此Πt的演化可視為一個馬爾科夫過程,記為
(9)
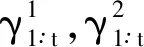
系統尋求納什均衡問題最終簡化為尋找Πt的馬爾科夫完美均衡問題。下面將介紹貝葉斯博弈條件下一種改進的尋找馬爾科夫完美均衡算法。
步驟1:初始T時刻,?π∈Πt,狀態xt的概率分布、動作集及其代價函數如下:

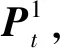

(10)
式中:Ui為控制器i(i=1,2)的動作集合;Zt+1為公共信息的增量;Mi為控制器的資源限制數量;j≠i,i,j=1,2。
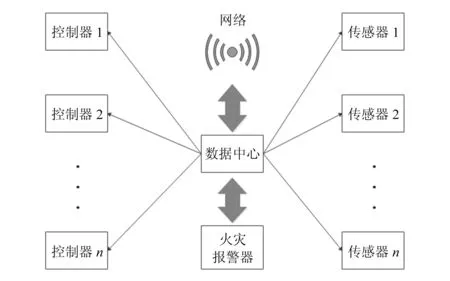
步驟2:當t 圖1所示為一個簡化的火警網絡控制模型,數據中心通過網絡接收傳感器搜集的環境信息,如空氣濕度、煙霧濃度、溫度、光照強度等。如果發現火災,將產生警報信息并發送給控制器執行各類指令,如打開應急燈、關閉電梯、開啟消防噴頭等。 圖1 簡化的火警網絡控制模型 (11) 此外,控制器1能夠完全觀測信息,控制器2觀測誤差率為1/3,則有 (12) 令各控制器資源上限Mi=1,且在一個時間步長后分享觀測與動作集。在t時刻,公共信息與私有信息計算式如下: (13) (14) 式中:π(X2=1)為當X2=1時在分布下π的概率。 同理,當t=1時,δ1(x)=1-x,δ2(y)=1-y為博弈過程的貝葉斯納什均衡。代價為: (15) 案例結果可為不完全信息、資源受限條件下博弈雙方策略的選取提供借鑒。 進一步,令各控制器資源受限閾值Mi=25,系統噪聲服從標準正態分布,各狀態轉移(信息演化)過程服從Sigmod函數,即: (16) 隨著控制器增多,本文方法與Markov方法下的博弈過程中納什均衡策略的最大執行策略數如圖2所示。可以看出,隨著系統控制器增多,兩種方法下各控制器可獲取資源不斷增加,這種情況符合實際規律。本文方法由于考慮了資源受限情況,系統執行均滿足資源受限要求,然而Markov方法存在控制器在博弈時超過可獲取的資源數量限制Mi=25。 圖2 不同算法下控制器數量與控制器最大執行策略數關系 本文研究了網絡安全中攻防沖突雙方信息獲取不完整以及資源受限條件下的動態博弈問題,并提出了一種改進的尋找馬爾科夫完美均衡算法。案例結果為不完全信息、資源受限條件下博弈雙方策略選取提供了一定借鑒。但是,目前的研究工作僅考慮了資源受限情況,未考慮觀測過程中干擾、時延等帶來的誤差問題,故要真正在實踐中體現其價值,還需要進行后續研究。
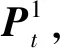

3 案例與分析
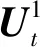

4 結束語

