基于隨機游走的改進標簽傳播算法

鄭文萍，岳香豆，楊 貴

（1.山西大學計算機與信息技術學院，太原 030006；2.計算智能與中文信息處理教育部重點實驗室（山西大學），太原 030006）

（?通信作者電子郵箱wpzheng@sxu.edu.cn）

0 引言

在現實生活中，網絡無處不在。例如，在社會學中網絡表示人與人之間的關系［1］；在生物學中網絡可以用于研究生物體內的代謝過程［2-3］；除此之外，網絡還在物理學［4］、醫學［5］、信息科學等方面都有很廣泛的應用。網絡可以被建模為圖，圖中的節點表示系統中的各個實體，而邊表示為實體間的關系。真實世界網絡通常由一系列功能模塊組成，具有很復雜的連接模式，其具有的一個非常重要的潛在特征是社區結構（community structure）。通常情況下，網絡中的社區內部的節點間連接較為緊密，而社區間節點的連接相對稀疏［6］。社區發現算法可以對網絡中的社區進行識別，將網絡分成不同的功能單元，以便于更好地揭示網絡的隱藏結構。它可以廣泛地應用于公眾情緒分析、用戶流失率預測、商品推薦等。

最近幾年，社區發現算法被廣泛地提出，引起了研究者們廣泛的興趣。研究者利用了生物學、物理學、社會科學、應用數學和計算機科學等不同學科的知識開發了很多社區檢測的算法［7］。根據求解策略的不同，可以將這些社區發現算法分為兩類：基于優化的算法和基于啟發式的算法［8］。其中，基于優化的算法是設置一個或多個目標函數，然后不斷地對這些目標函數進行優化，直到得到最優解，其代表性的方法是譜聚類方法［9］和模塊最大化方法。譜聚類的方法是將社區檢測問題轉化為優化二項式的問題，通過拉普拉斯矩陣的特征值和特征向量來對網絡進行表示并對網絡進行近似最優劃分。基于模塊性最大化方法是將模塊性設為目標函數，并不斷地對模塊性進行優化，直到模塊性達到最大值的方法，如Girvan-Newman（GN）算法［10］、快速Newman（Fast Newman，FN）算法［11］以及BGLL（Blondel VD，Guillaume JL，Lambiotte R and Lefebvre E）算法［12］等。

基于啟發式的方法是設置一個啟發式規則并利用這個規則來尋找社區的最優分。Palla 等［13］在2005 年提出的派系過濾算法是啟發式方法中的一種代表性方法。2007 年，Raghavan 等［14］提出的標簽傳播算法（Label Propagation Algorithm，LPA）是社區發現算法中最快的算法之一。該算法受到流行病傳播的啟發，通過節點標簽的迭代傳播直到收斂來檢測社區。由于該算法具有線性的時間復雜度并且過程比較簡單，因此可以用于大型網絡的社區發現。LPA 首先給網絡中的每個節點賦予唯一的初始標簽，然后按照隨機產生的節點序列對節點進行遍歷，將鄰域中出現頻率最高的標簽作為當前節點的社區標簽，此過程迭代進行，直到所有節點的標簽達到穩定。由于LPA 在社區劃分中存在隨機過程，使得劃分結果有很大的不穩定性，現有很多方法對其進行了改進。為了找到重疊社區，提出了重疊社區傳播檢測算法（Community Overlap PRopagation Algorithm，COPRA）［15］和基于信息通信的LPA（Speaker-listener LPA，SLPA）算法［16］。除此之外，Barber 等［17］提出了一種基于模塊度優化的LPA（modularity-specialized LPA，LPAm）來避免LPA 在運行過程中形成一個大的社區。LPAm 在LPA 中加入約束條件，通過設定目標函數來約束迭代傳播的過程，然后將社區模塊性值作為另一個目標函數，將社區檢測問題最終轉化為目標函數的優化問題，但是在算法過程中，最終的結果可能會陷入局部極大值的情況。針對此問題，Liu 等［18］提出了LPAm+對LPAm進行改進，在LPAm 的基礎上加入了合并不同社區并使得模塊最大化的過程，使得算法可以重新達到一個最大局部極值。Li 等［19］提出了一種兩階段的標簽傳播算法LPA-S（Stepping community detection Algorithm based on Label Propagation）：在算法的第一階段對節點對之間的相似性進行計算，標簽在該節點鄰域內相似性較大的節點間進行傳播，得到初始的社區劃分；在第二階段將初始劃分后的社區看為節點，并進行社區間相似性的計算，合并相似社區，最終所得社區具有最大的目標函數。鄭文萍等［20］在2018 年提出了一種基于標簽傳播的兩階段社區發現算法（Two-Stage community detection Algorithm based on Label Propagation，LPA-TS）：該方法定義了節點的參與系數，確定節點的更新順序，并在標簽傳播中根據節點的相似性來更新節點標簽，得到初始劃分；在第二階段按照參與系數來進行社區的合并，得到最終的社區劃分效果。宋琛等［21］在2016 年提出一種基于隨機游走相似度矩陣的改進標簽傳播算法，通過隨機游走得到節點的相似度矩陣，并在節點標簽更新時，按照相似度矩陣中概率來對節點的鄰居節點的標簽進行選擇和更新。在這些改進算法中，可以看出大部分算法都是只對標簽傳播算法的標簽更新規則進行改進，沒有考慮節點初始標簽和更新順序的隨機性對算法結果穩定性的影響。本文將綜合考慮節點標簽的初始化和節點更新順序對標簽傳播算法的影響。

針對節點初始標簽和更新順序隨機性導致社區發現結果不穩定的問題，本文提出了一種基于隨機游走的改進標簽傳播算法（improved Label Propagation Algorithm based on Random Walk，LPARW），減少了由于標簽更新順序的隨機性和在算法初始階段給每個節點都賦予標簽而導致的算法的不穩定性。通過將LPARW 與經典的社區發現算法在真實網絡數據集上進行實驗比較，發現LPARW 在標準互信息（Normalized Mutual Information，NMI）、調整蘭德系數（Adjusted Rand Index，ARI）、模塊性等方面都表現得比較好。

基于改進LPA的準確性與穩定性，本文的主要工作如下：

1）通過計算隨機游走的位置概率分布來對節點重要性進行一個初始的度量。

2）引入了節點相似性的計算，在隨機游走的基礎上，確定了種子節點。

3）只給種子節點賦予標簽，通過特定的傳播規律來對種子節點的標簽在網絡中進行擴散，使得標簽傳播算法得到的社區劃分結果更加穩定。

1 背景知識

用G=(V，E)來表示一個網絡圖，其中，V={v1，v2，…，vn}表示網絡中所有節點的集合，每個節點由vi表示，n表示網絡中的節點數；E={e1，e2，…，em}表示邊的集合，即為節點與節點之間的聯系。在集合E中的每條邊都在集合V中有一對節點與之對應。根據網絡中的邊是有向的還是無向的以及邊上是否有權重，可以將網絡分為加權有向圖、加權無向圖、無權有向圖以及無權無向圖。本文主要對無權無向圖進行研究。通常，使用鄰接矩陣An×n來對圖進行表示，其中：

無權無向圖的鄰接矩陣是對稱矩陣，即aij=aji。節點的度是復雜網絡中節點屬性的最重要的概念。一個節點的度即為與這個節點直接相連的節點的數量，而與這個節點直接相連的節點即為該節點的鄰域，即NG(vi)={vj|(vi，vj)∈E}。節點的相似性度量有很多種度量方法，可以大致地分為基于局部信息的節點相似性指標和基于全局的節點相似性指標。其中，在基于局部信息的節點相似性指標中最常用的是基于節點之間的公共鄰居來對節點的相似性進行度量，如公共鄰居（Common Neighbors，CN）指標、Salton 指標［22］和Jaccard 指標［23］等。基于節點之間公共鄰居相似性指標認為，任意兩個節點之間的相似性取決于其公共鄰居數，二者的公共鄰居越多，則它們就越相似，從而這兩個節點間有連邊的可能性也越大。

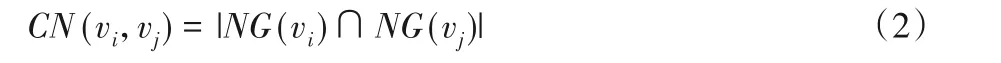
Jaccard 相似性是利用兩個節點之間的交集和并集的比例來定義的，比值越高，則證明這兩個節點有更高的相似性，由式（3）表示：

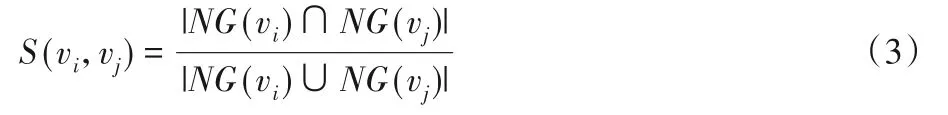
2 基于隨機游走的改進標簽傳播算法

基于標簽傳播算法的不穩定性，本文提出了一種基于隨機游走的改進標簽傳播算法（LPARW），通過隨機游走得到的每個節點的到達概率即為節點的重要性，對重要性進行降序排序從而確定節點的標簽更新順序。根據節點標簽更新順序對節點進行遍歷，使用相似性公式對節點之間相似性進行計算，選擇出最終的種子節點，對每個種子節點賦予初始的標簽。最后，將剩余的節點進行標簽傳播得到最終的社區劃分結果。LPARW 通過確定節點的更新順序，減少了傳統的標簽傳播算法由于節點標簽更新順序的隨機性而導致的最終劃分結果的不確定性。傳統LPA在初始化階段對每個節點都賦予唯一的社區標簽，在標簽傳播過程中，一些重要節點的社區標簽可能會被覆蓋，進而導致社區發現結果不穩定。為了改進此情況，本文算法LPARW 只對選擇出的種子節點賦予社區標簽，并在網絡中進行標簽傳播。由于種子節點對應網絡中的重要節點，其性能比較穩定，因而也提高了社區發現結果的穩定性。

2.1 種子節點的確定

在LPARW 中，考慮到LPA 選擇標簽時的隨機性，將每個節點賦予初始標簽進行傳播時會增強算法最后劃分的社區結果的隨機性，而且原始的LPA 中節點的標簽更新的次序是隨機的，會很大程度上影響社區劃分的最終結果。因此，在標簽初始化的過程中只為選擇的種子節點賦予標簽可以減少初始標簽的個數，也可以避免由于標簽更新順序不同而造成的社區劃分結果的不穩定性，進而擴大有用標簽的影響力，提高社區發現的準確率。

馬爾可夫聚類（Markov CLustering，MCL）算法［24］是對隨機游走進行仿真。MCL 在復雜網絡中是一個動態的過程，游走者以一定的概率不斷從一個節點移動到另一個節點。根據隨機游走方法，如果一個節點作為隨機游走結束時到達的節點的概率越高，則意味著這個節點的影響力越大。LPARW 使用隨機游走最終的可能位置分布來衡量網絡中節點的重要性。在隨機游走的過程中，布朗粒子到達其鄰居節點的概率由式（4）來表示：

利用式（4）可得到節點的一步游走的概率分布矩陣。對每個節點多步隨機游走的可能概率分布進行疊加可得到網絡最終的隨機游走概率矩陣。若節點的概率分布越高，則證明該節點與更多的節點相似，而一個節點與越多的節點相似，則證明這個節點的重要性越大。每一步的位置分布概率可以由指示向量I和矩陣P的乘積表示。t步之后，游走者位置分布概率可由式（5）表示：

其中，I0為單位向量。將It進行降序排序，可得到更新序列。序列中越靠前的節點作為種子節點的可能性越大；相反，序列中越靠后的節點影響力越小，其作為種子節點的概率也越小。

將所有節點按照影響力大小進行排序，得到節點的更新序列。按照節點的更新序列對節點的標簽進行更新，可以減少原始LPA中由于更新序列的隨機性而導致的社區發現結果的不穩定性。

基于種子節點的社區發現算法的缺點是需要提前確定種子的個數，而社區發現算法中，社區的個數往往都是未知的，因此種子節點的確定是非常困難的。LPARW 不需要提前確定種子的數量，該算法通過使用相似性度量來對節點的相似性進行度量從而確定最終的種子節點。在本文中使用節點的公共鄰居來對兩個節點的相似性進行度量：兩個節點的公共鄰居數越多，則這兩個節點結構越相似，屬于同一個社區的可能性越大，這樣得到的劃分結果更符合原來的社區分布，而眾所周知，節點的度是刻畫單個節點屬性的最簡單而又最重要的概念之一［25］。無向網絡中節點的度被定義為與節點直接有邊連接的其他節點的數目。本文給出了節點之間計算相似性的計算公式，由式（6）表示。

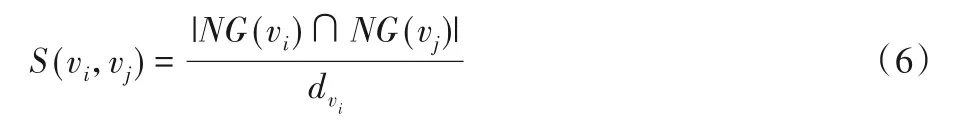
其中：NG(vi)為節點vi的一階鄰居節點的集合；NG(vj)為節點vj的鄰居節點的集合；dvi為節點vi的度。

LPARW 中，遍歷節點更新序列，將當前節點與更新序列在其之前的節點進行相似性的計算：若當前節點與更新序列在其之前的某個節點是相鄰節點，且相似性指標小于閾值，如果該節點的標簽為空值，則將序列在其之前的節點選擇為種子節點；否則不選為種子節點。在Karate網絡中LPARW 選擇出的種子節點如圖1所示。

圖1 Karate網絡上得到的種子節點Fig.1 Seed nodes obtained on Karate network

2.2 標簽的更新策略

傳統的LPA在標簽更新過程根據其鄰域中標簽數量最多的標簽來更新自己的標簽。當鄰域中最大數量的標簽數有多個的時候，則隨機選擇一個標簽作為自己的標簽。這樣會使得標簽產生震蕩，導致社區發現結果的不穩定性和隨機性，并且在原始的標簽傳播算法的初始階段每個節點都有標簽，在傳播過程中會導致不重要的標簽有可能會影響標簽傳播算法的最終的社區劃分的結果。

LPARW 將種子節點的節點標號作為種子節點的標簽，其余節點的標簽設為空值。在第一次的標簽傳播的過程中，根據當前節點的標簽和種子節點的鄰居節點的公共鄰域的個數以及該節點本身的度數來決定該節點是否接受種子節點的標簽，而不是像傳統的LPA將節點標簽的重要性考慮為相同的，由此可以減少標簽的隨機選擇而導致的最終劃分結果的不穩定性。當節點鄰域內滿足條件的種子節點只有一個時，則節點選擇該種子節點的標簽作為節點的標簽，若滿足條件的種子節點有多個時，則選擇出現次數最多的標簽作為節點的標簽。在對所有種子節點的一階鄰域標簽傳播完成后，剩余的標簽為空的節點根據公式進行標簽的更新。

2.3 算法描述

首先，將網絡中所有節點的標簽都賦為空值；然后，根據隨機游走生成的隨機序列對這個隨機序列進行降序排序，將該序列作為標簽傳播過程中節點標簽的更新序列。根據節點的更新序列來對節點進行遍歷。在遍歷過程中，將當前節點和在更新序列中位于當前節點前面的所有節點的公共鄰域的數量以及其本身的度進行相似性的比較，若有節點vi-1與當前節點vi是相鄰的節點且相似性大于選定的閾值，節點vi-1的標簽為空值時，則將節點vi-1選為種子節點并將其節點標號作為節點vi的標簽，依次循環，選出所有的種子節點并完成種子節點直接鄰域的標簽傳播過程。在第一次標簽更新完成后，對剩余標簽為空的節點按照原始的標簽傳播算法的更新標簽過程進行更新。以上標簽更新過程迭代進行，直到標簽達到穩定。下面給出LPARW的社區發現過程。

算法1 基于隨機游走的改進標簽傳播算法。

輸入 網絡G=(V，E)，閾值λ；

輸出 網絡的劃分結果。

步驟1 根據馬爾可夫隨機游走，生成可能作為游走終止節點的概率分布矩陣，按照式（5）形成節點集合的降序序列B={i1，i2，…，in}。

步驟2 對1 ≤j≤n，令L(ij)={}；令t=1，seed={}。

步驟3t=t+1，j=1；如果t>n，轉步驟5。

步驟4j=j+1，如果j≥t，轉步驟3。

步驟4.1 若邊(it，ij)?E，則轉步驟4；

步驟4.2 根據式（6）計算節點it與節點ij的相似性，如果s(it，ij)<λ，則轉步驟4；

步驟4.3 如果ij∈seed，則令L(it) ∪{j}；

步驟4.4 如果ij∈seed且L(ij)={}，則令seed=seed∪{ij}，L(ij)={j}，L(it)=L(it) ∪{j}；

步驟4.5 如果ij∈seed且L(ij) ≠{}，則令L(it)=L(it)∪L(ij)；

步驟4.6 轉步驟4。

步驟5 若網絡中存在節點v有多個標簽，選擇其鄰域內出現次數最多的標簽作為v的標簽。

步驟6 若網絡中存在標簽為空的節點v，按照式（6）計算v與種子集seed中相鄰節點相似性。若s(v，w) ≥λ，則令L(v)=L(v)∪L(w)。若有多個種子節點滿足條件，則選擇標簽出現次數最多的作為自己的標簽。如果對節點v不存在滿足條件的相鄰種子節點，則保持v的標簽為空。

步驟7 設當前網絡中標簽為空的節點集為-V。

步驟8 對-V中節點v，選擇其鄰居節點中出現次數最多的標簽作為v的標簽。重復此步驟，直到-V中節點的標簽不再變化，得到最終的社區劃分結果。

3 實驗與結果分析

實驗平臺是Intel Xeon CPU（3.10 GHz），32 GB 內存，Windows 10 系統，所有算法均采用Python 實驗。為了驗證LPARW 的準確性和穩定性，將LPARW 在Karate、Dolphin、Football、Polbooks、blogs、Router、rt_ksa、Router_views、PGP 等網絡上進行實驗，并與LPA、LPAm、LPAm+和LPA-S 等標簽傳播的經典算法和改進算法進行比較。

3.1 評價指標

此處采用標準互信息（NMI）與調整蘭德系數（ARI）對有標簽的各算法在有標簽網絡上的社區發現結果進行評價。NMI被廣泛地用于檢測社區劃分結果的好壞。如果算法社區劃分的結果與真實社區結果非常接近，則它的值接近于1，否則NMI 的值接近于0。ARI 是基于兩個方法在相同的社區劃分下，節點相同的概率。對于一個有n個節點的集合V，B={B1，B2，…，Bk'}表示一個網絡劃分結果，A={A1，A2，…，Ak}表示網絡原始劃分。NMI和ARI的定義如式（7）和式（8）所示。

對于無標簽數據集，本文采用模塊性進行度量。模塊度是一種衡量社區劃分質量的標準，其基本想法是將隨機網絡作為零模型，比較所發現社區的模塊度與零模型網絡模塊度的差異，差異越大則社區發現質量越好。模塊度Q的定義如式（9）所示。

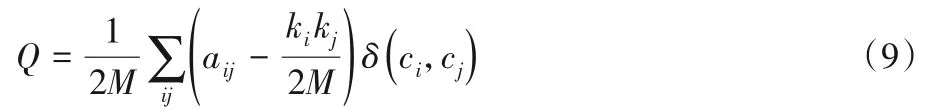
其中：aij表示鄰接矩陣中的元素，若節點i和節點j之間有連邊，則aij等于1，否則等于表示隨機網絡中節點i和節點j的連邊數的期望值。

3.2 結果分析

為了驗證LPARW 的性能，在空手道俱樂部（Zachary’s Karate Club）、海豚社交網絡（Dolphins Social Network）［26-27］、大學生足球網絡（American College Football Network）［28］和Polbooks 這4 個帶標簽的真實網絡和blogs、Router、rt_ksa、Router_views、PGP這5個無標簽的真實網絡上，與基于LPA改進的算法LPAm、LPAm+、LPA-S 和LPA-TS 等比較。數據集基本情況如表1所示。

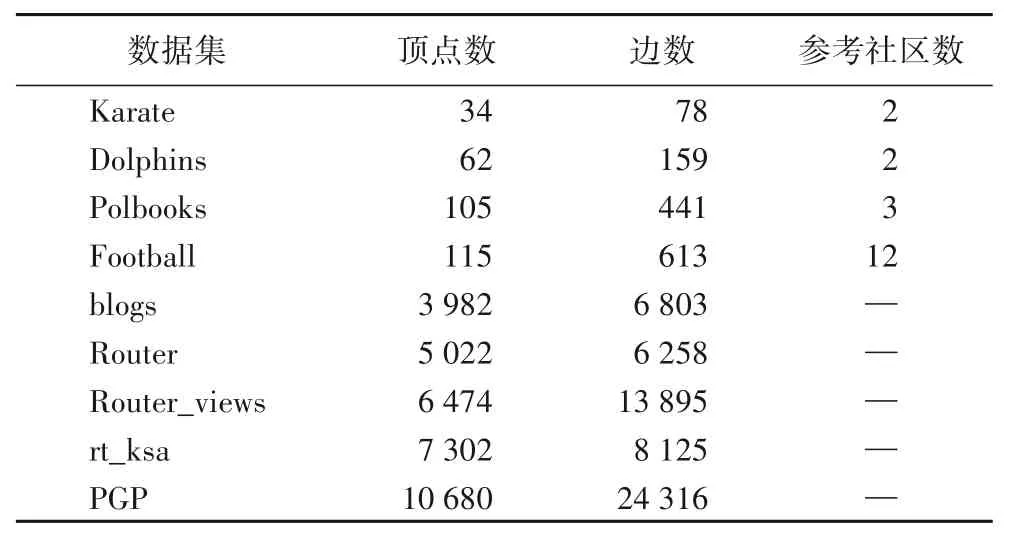
表1 真實網絡數據集基本信息Tab.1 Basic information of real network datasets

由于標簽傳播算法社區發現結果不穩定，因此將本文算法及對比算法在每個網絡上分別運行30 次，計算最終所得社區的NMI、ARI 和模塊度Q等評價指標的平均值作為最終算法性能，比較結果如表2 所示，其中K表示算法最終發現的社區個數。由于對比算法LPA、LPAm、LPAm+、LPA-S和LPA-TS等各次運行結果所得的社區個數相差較大，無法用具體值描述，表2中用“—”表示。

表2 給出了各個算法在有標簽的網絡數據集中的實驗對比結果。由表2 可以看出，在Karate 和Dolphins 網絡中，LPARW 的NMI 和ARI 值達到了1，即算法的社區發現結果與原始的劃分完全一致。同時，在其余兩個網絡中，LPARW 的NMI 和ARI 值也達到了最高，并且該算法發現的社區個數是非常穩定的。因此可以看出，本文算法在有標簽的網絡數據集中表現良好。

表2 帶標簽真實網絡實驗結果對比Tab.2 Comparison of experiment results in labeled real networks

圖2 給出了本文算法在Karate 網絡上的劃分結果。由圖2可以看出，LPARW 將Karate網絡穩定地劃分為兩個社區，這與原始的網絡劃分是一致的。該網絡是由34 個節點組成的，網絡中的節點表示俱樂部的所有成員，邊表示這些成員之間的關系。可以看出，LPARW 的劃分結果與原始社區的標簽完全一致。

圖2 LPARW在Karate網絡上的劃分結果Fig.2 Division result of Karate network by LPARW

圖3 給出了本文算法LPARW 在Dolphins 網絡上的劃分結果。Dolphins是人們通過對新西蘭神奇灣的62只海豚進行長期的觀察而得到的網絡。其中，節點表示海豚，邊表示海豚之間的相互聯系。經過長期觀察，海豚的活動群體分成兩個群體，并且每個群體在不同的活動范圍內活動，所以Dolphins網絡有兩個社區，LPARW 可以穩定地劃分出兩個社區。由圖3 可以看出，LPARW 算法的劃分結果與原始網絡的社區劃分結果是完全一致的。

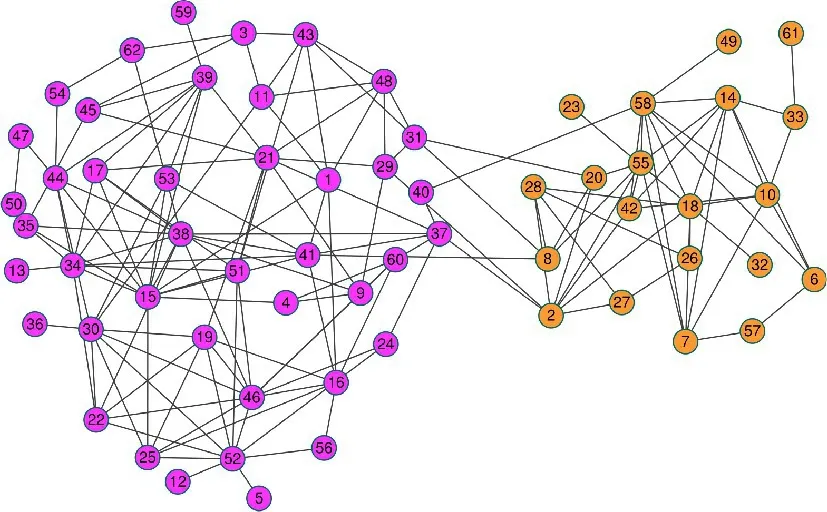
圖3 LPARW在Dolphins網絡上的劃分結果Fig.3 Division result of Dolphins network by LPARW

圖4 給出了Polbooks 網絡的原始劃分，圖5 給出了本文算法在Polbooks 網絡上的劃分結果。Polbooks 網絡節點表示在Amazon 在線書店上銷售的與美國政治相關的圖書，邊表示兩本圖書是否被同一用戶購買過。這些圖書被分為3 類：“自由派”“保守派”和“中間派”。

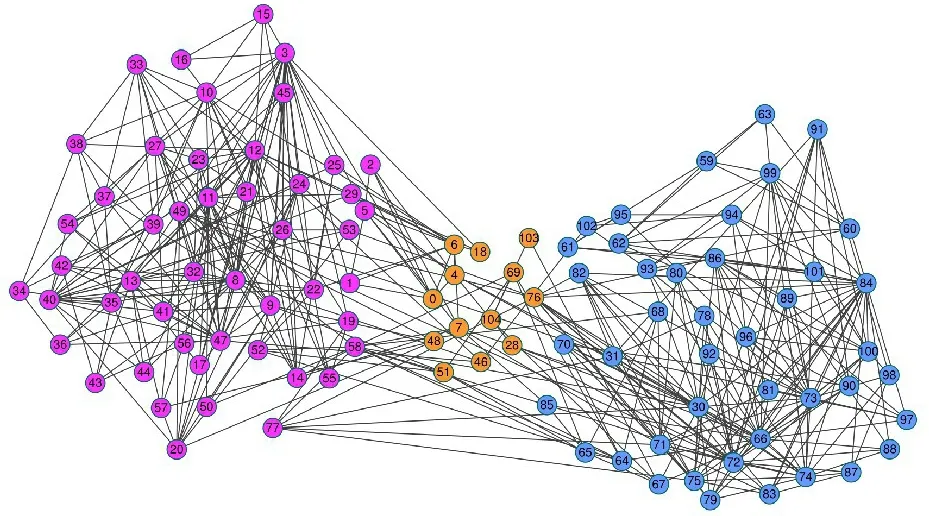
圖4 Polbooks網絡原始的劃分結果Fig.4 Original division results of Polbooks network

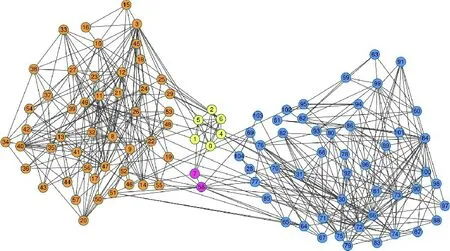
圖5 LPARW在Polbooks網絡上的劃分結果Fig.5 Division result of Polbooks network by LPARW

圖6 給出了原始的Football 網絡的劃分結果。Football 網絡是美國高校代表隊參加2000 年的賽季比賽的比賽情況。其中，節點表示高校的橄欖球代表隊，若兩支球隊之間至少有過一次比賽的話，則這兩個球隊之間有一條邊。由于每個球隊屬于不同的聯盟，共有12 個聯盟，所以，Football 網絡會被劃分為12個不同的社區。

圖7 給出了LPARW 在Football 網絡上的社區劃分結果。由表2 可以看出，LPARW 相較其他的算法有更高的NMI 和ARI 值，該算法可以將網絡的社區穩定地劃分為13 個不同的社區。LPARW 相較其他算法的劃分結果是最接近原始的劃分結果的。

表3 給出了LPARW 在5 個真實的沒有標簽的網絡上與其余5種LPA、LPAm、LPAm+、LPA-S、LPA-TS經典算法在Q值上的對比。可以從表3 中很明顯地看出，在大部分的數據集上，LPARW的Q值最高，且社區個數穩定，算法性能最好。

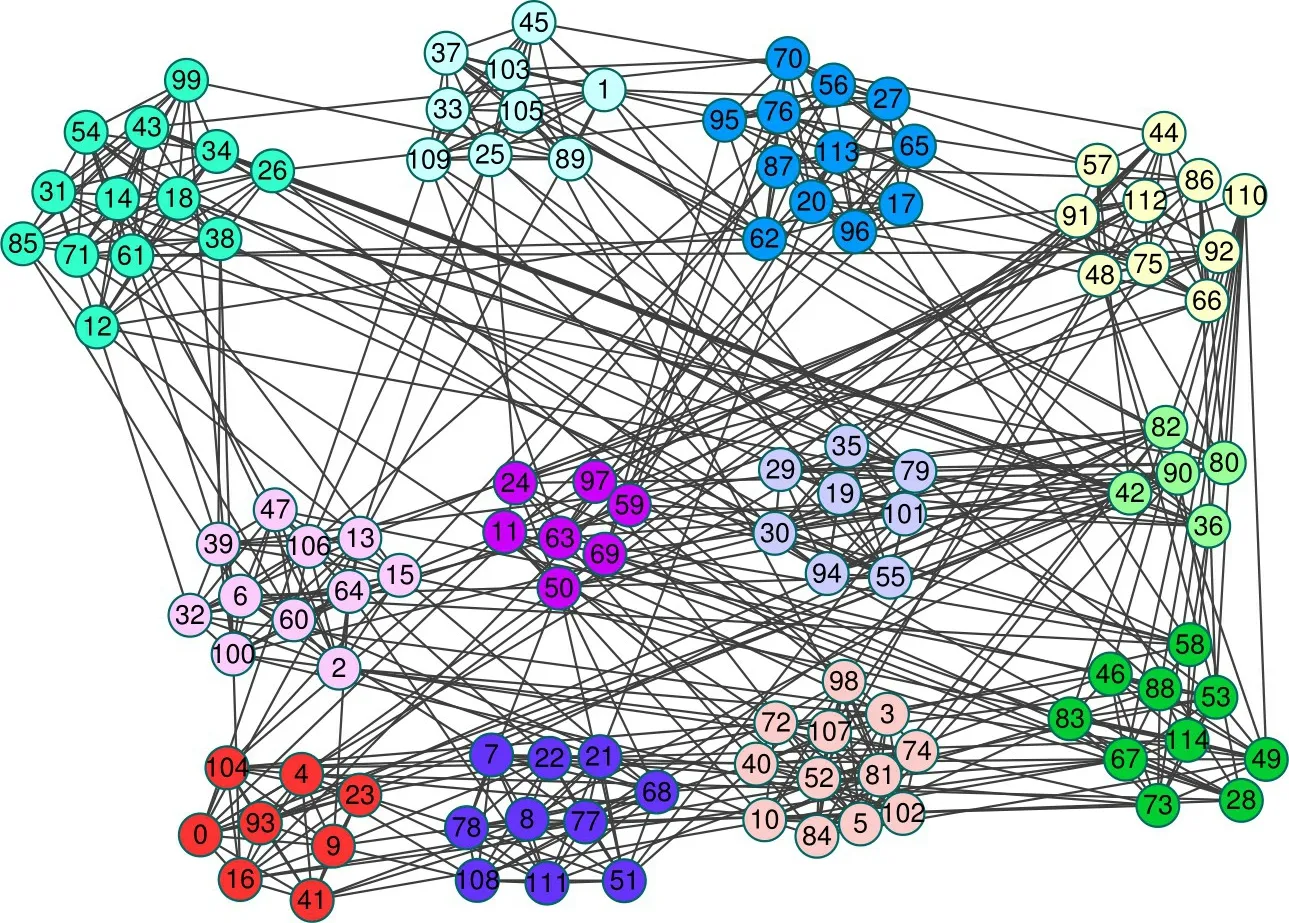
圖6 Football網絡原始的劃分結果Fig.6 Original division results of Football network

圖7 LPARW在Football網絡上的劃分結果Fig.7 Division result of Football network by LPARW

表3 無標簽真實網絡Q值對比Tab.3 Comparison of Q value in unlabeled real networks

4 結語

本文提出了一種基于隨機游走的改進標簽傳播算法，由于考慮到在原始的標簽傳播中若給每個節點都分配標簽，會增加其余標簽對最終社區劃分結果的影響，增加算法的不穩定性，所以LPARW 在標簽傳播過程的賦予初始標簽階段只給影響力大節點賦予標簽，然后對其余節點進行標簽的傳播，這樣會增加算法的穩定性，優化算法的最終社區劃分的結果。在確定影響力大的節點時，LPARW 使用了隨機游走和相似性指標。在生成更新序列時，LPARW 采用隨機游走，并對每個節點的可能概率分布進行疊加后生成更新序列，固定了節點標簽的更新順序。在對節點更新序列進行遍歷階段，確定了種子節點及種子節點直接鄰域的節點的標簽。將剩余的沒有標簽的節點進行遍歷并按照選擇鄰域節點的標簽的最大值來確定標簽。通過以上步驟，得到了最終的社區劃分結果。通過與經典的社區發現算法LPA、LPAm、LPAm+、LPA-S和LPATS 等在4 個有標簽的真實網絡數據集以及5 個無標簽的真實網絡數據集上進行分析比較，實驗結果表明，本文算法在NMI、ARI和模塊度Q等方面的指標均優于其余的經典的標簽傳播社區發現算法，表明該算法有很好的社區劃分效果。在今后的工作中，對于該算法如何應用于重疊社區將進行進一步的研究。