基于三維時空地圖和運動分解的多機器人路徑規劃算法
屈立成,呂 嬌,趙 明,王海飛,屈藝華
(長安大學信息工程學院,西安 710064)
(?通信作者郵箱qlc@chd.edu.cn)
0 引言
利用機器人完成重復繁重的搬運任務是一個高效快捷的物品搬運方法,如自動物流分揀系統、智能倉儲系統、智能泊車系統等。在一個機器人系統中,多個移動機器人同時協同完成給定的任務集可以有效減少系統的總耗時,但不同的機器人的運動路徑可能存在沖突、死鎖等問題,如果不能有效地解決上述問題,多機器人系統的穩定性無法得到保障,不能充分發揮多機器人系統的并行運行特點,即系統在同一時刻以最低代價使得盡可能多的機器人可以同時互不影響地獨立運行,可以說多機器人路徑規劃已經成為當前機器人熱門研究方向之一。
多機器人路徑規劃是指每個機器人在已知地形圖中根據給定的目標終點及當前出發節點規劃出一條無碰撞的最優路徑,并且要求系統總代價最小。多機器人路徑規劃是一個NP-Hard(Non-deterministic Polynomial-Hard)問題[1-2],當前并無很好的解決方案。近些年來不少學者將人工勢場[3-6]、蟻群算法[7-9]、A*算法[10-11]、遺傳算法[12-14]、神經網絡[14-15]等理論運用于多機器人路徑規劃系統中。然而,這些算法大多得到的是次優解而不是最優解,整個多機器人系統的運行效率較低。
早期對多機器人的研究多采用集中式路徑規劃策略,其中:王佳溶等[16]提出了基于改進的兩階段控制理論的AGV(Automated Guided Vehicle)控制調度策略,利用遺傳算法生成離線路徑庫,采用速度調節對其進行在線動態路徑規劃,若生成的路徑不滿足條件,則使用帶約束多目標遺傳算法在線計算路徑,增加了AGV 調度系統的靈活性。Luna等[17]提出了一種高效完整的集中式多機器人路徑規劃方法,采用了“推”和“交換”兩種原語,不僅提高了解的質量,同時也減少了多機器人系統的計算時間。不同于離線路徑生成階段和在線路徑規劃的規劃策略,夏清松等[18]提出了基于路徑規劃層和碰撞避免層的多機器人路徑規劃策略:在第一層只考慮單一機器人的路徑規劃,忽略其他機器人的影響,其規劃的路徑可能會與其他機器人產生嚴重碰撞;在第二層采用碰撞避免規則解決多機器人的局部碰撞,其避碰規則復雜,且需要人為提前制定,無法根據多機器人系統當前特點改變。
一些研究者另辟蹊徑,采用分布式路徑規劃模型,將路徑規劃的計算任務放到機器人自身的處理器上,機器人之間共享地圖信息,解決了傳統多機器人系統路徑計算嚴重依賴中央路徑規劃模塊的問題。這一類模型必須要解決的主要問題為機器人必須實時接收和發送地圖數據,這些數據量一般較大。為解決上述問題,Matoui 等[19]提出了一種基于鄰域人工勢場的多機器人分布式路徑規劃方法,利用分布式體系結構規劃移動機器人軌跡,采用改進的人工市場方法使多機器人系統獲得良好的軌跡規劃,提高了多機器人系統的魯棒性;結合分布式路徑規劃和集中式協調思想,曹其新等[20]提出了基于保留分區的分布式多機器人路徑規劃策略,采用分布式規劃架構,機器人與中央模塊通過保留分區協調路徑碰撞可能情況,每個機器人都向中央模塊發送分區請求,中央模塊通過計算后將保留分區下發至每個機器人,機器人按照接收的保留分區信息運動,這種策略沒有有效考慮多機器人系統可能產生的不確定因素,系統只能在每個機器人都按照接收的保留分區運動后,才能繼續下一步計算。由于自動物流分揀系統以及智能倉儲系統中,任務的產生是隨機且連續的,多機器人系統必須能夠持續完成任務,而對于集中式規劃算法側重的是對任務集的一次全局規劃,不能靈活地處理隨機連續產生的任務。多機器人系統采用分布式路徑規劃策略后,單個機器人作為計算的最小單元,系統可以高效地完成給定任務集合,持續完成產生的任務,因此本文采用分布式多機器人路徑規劃策略。
本文提出了基于三維時空地圖和運動分解的多機器人路徑規劃算法。路徑搜索空間在z軸方向只能單向遞增,因為z軸代表時間軸,時間只能向前,無法倒退,不同于一般意義的三維空間,故這里的三維時空地圖實際為帶約束三維時空。所提算法首先使用柵格法構建地圖環境模型,在其垂直坐標軸上拓展為時間軸,構成帶約束三維時空地圖,其中可以存儲所有機器人在當前時刻至最大時間刻度范圍內的已規劃路徑、機器人在無任務時的駐車位置信息,以及地圖中存在的障礙物位置信息。機器人根據其接收的任務,采用帶條件深度優先搜索(Depth First Search,DFS)算法優先遍歷最有可能是最優路徑的路徑集合,可以有效解決隨機持續倉儲任務的問題。仿真實驗結果表明,本文算法規劃的路徑為最優路徑,且具有無碰撞、魯棒性高、可同時運動機器人數量多等優點。
1 問題描述
多機器人路徑規劃是指在一個地圖環境已知條件下根據機器人集合Robots={r1,r2,…,ri,…,rn}和任務集合Tasks={t1,t2,…,tj,…,tm}規劃出系統最優無碰撞運行路徑集,任務集合中任務產生的時間并無規律。其中:ri表示第i個機器人,tj表示第j個運動任務,tj={start,end}包括任務的起點start和終點end,n表示機器人數量,m表示任務數量。
為了更加直觀地表示二維柵格地圖中各個空間位置的連通關系,將可用的空間位置抽象為節點,并用連線表示節點間的有效路徑,既便于地圖的直觀展示,又便于采用數學方法對其進行分析。在傳統的二維柵格地圖中,機器人只能在二維坐標空間上進行區分,無法表現其在時間維度上的發展變化。如圖1(a)中所示,兩個機器人的運動路徑在左側有重疊部分,無法在二維坐標空間內觀察這兩個機器人運動路徑的沖突情況。因此,在二維柵格地圖垂直平面上另行增加時間維度,即z軸,將二維平面提升至三維空間,形成了包含所有時刻機器人運動路徑及位置信息的三維時空柵格地圖,統一了機器人位置、障礙物和運動路徑等不同概念的表達方式,其維度提升示意圖如圖1(b)所示。
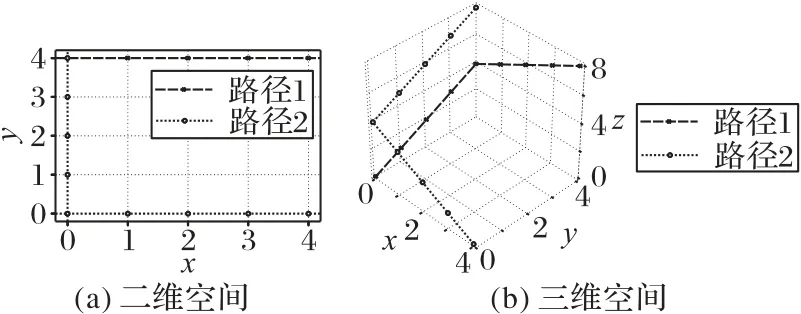
圖1 空間維度提升示意圖Fig.1 Schematic diagram of space dimension increasement
圖1(b)中,不同標記標注的線段表示不同的機器人將要執行的路徑,三維時空地圖中可以存儲所有機器人在當前時刻至最大時間刻度范圍內的已規劃的路徑、機器人在無任務時的駐車位置信息,以及地圖中存在的障礙物位置信息。
在平面z=0中,路徑與平面的交點表示當前時刻各機器人所處的二維位置,而在平面z=t中,路徑與平面的交點表示后續t時刻各機器人所處的位置。可以看到,三維時空地圖可以清晰地表示不同機器人的運動路徑,并且可以在時間維度上對在二維平面中的不同路徑加以區分。
本文采用分布式和集中式相結合的混合式的多機器人路徑規劃策略,將集中式里的中央控制模塊的大量路徑計算工作分散于每個機器人自身的處理器上,中央模塊僅負責相對簡單的地圖更新和任務分配工作。路徑規劃模型由n個機器人模塊、1 個中央通信模塊以及它們之間的通信鏈路組成,其應用概念如圖2所示。
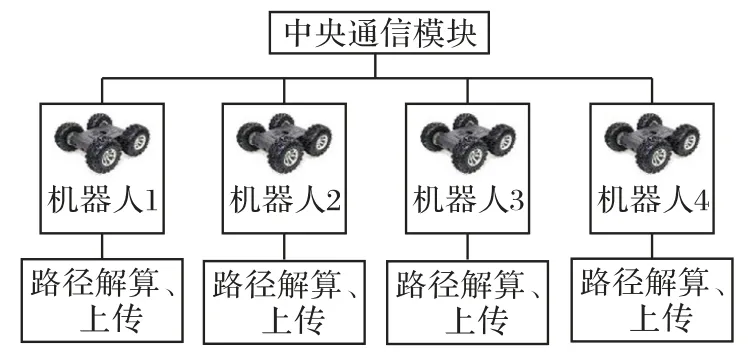
圖2 應用概念圖Fig.2 Application concept map
2 多機器人路徑規劃模型
可以考慮將單個機器人執行任務的總耗時分解為路徑運動時間、原地停留時間和轉向時間,從而可以將這些不同時間按照一定的規律組合,形成路徑集,而多機器人路徑規劃問題則轉化為在這些集合中尋找最優路徑問題。則機器人ri根據給定的路徑從起點運動至終點的時間表達式如下:
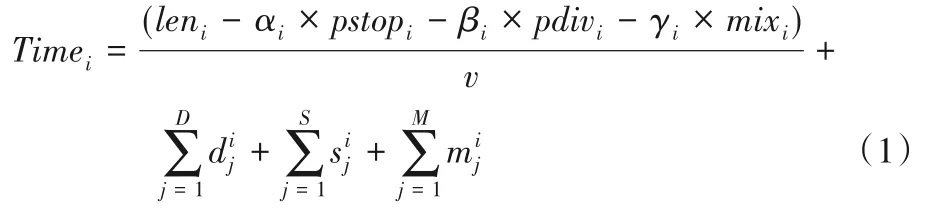
其中:leni是機器人ri從起點至終點所行駛的路徑長度;αi是機器人ri完成一次原地停留所需的單位長度;pstopi是機器人ri行駛過程中只包含原地停留的次數;βi是機器人ri完成一次轉向所需的單位長度;pdivi是機器人ri行駛過程中只包含轉向的次數;γi是機器人ri完成一次既是原地停留也是轉向(以下簡稱混合動作)所需的單位長度;mixi是機器人ri行駛過程中混合動作的次數;v是機器人ri穩定運動速度;D是機器人ri的轉向總次數;是機器人ri第j次轉向所耗費的時間;S是機器人ri的原地停止總次數;是機器人ri第j次原地停止所耗費的時間;M是機器人ri的混合動作總次數是機器人ri第j次混合動作所耗費的時間。
機器人ri從接受任務tj到完成任務tj所耗費的時間Totali如式(2)所示。
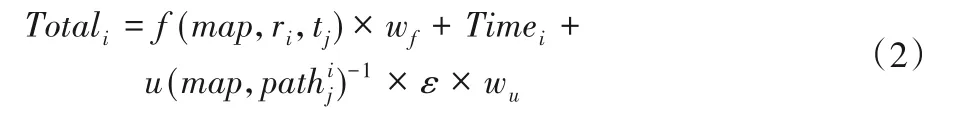
其中:map是二維柵格地圖垂直加上時間軸形成的三維時空圖;f(map,ri,tj)是機器人ri從輸入任務至其計算單元計算出路徑機器人ri本身所消耗的時間。由于多機器路徑規劃問題本身就是NP-Hard 問題,無法在多項式時間內計算出最終結果,只能在多項式時間內驗證一個解的正確性,這也就決定了路徑規劃的計算時間是不精確的,無法準確計算出其具體值。
這里f(map,ri,tj)是與在map中ri,tj所形成的矩形框拓展至三維空間內的空間復雜度正相關的函數,并不是真正的計算時間,而是對計算時間的估計;wf∈(0,1)是對計算時間估計的信任權重。u(map,)表示不確定時間,ε是對不確定時間的調節因子,wu∈(0,1)是不確定時間的信任權重。不確定時間表達式如式(3)所示:
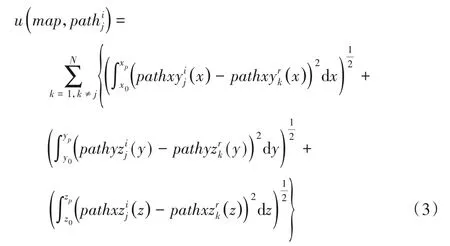
其中:P表示所有路徑的全集;sch表示一個多機器人系統的路徑規劃方案;? 表示所有規劃方案的全集。在自動分揀系統、智能倉儲系統以及其他多機器人應用場景下,任務的產生具有隨機性和持續性等特點,單次批量的集中式規劃算法并不適合這種場景下的多機器人路徑規劃,無法滿足系統對持續性任務的高靈活動態規劃要求。本文采用柵格法,并使用混合式多機器人路徑規劃方法,以達到每個任務的總耗費時間Totalj最小,由于任務的連續性、隨機性和不可預測性,只需要滿足單個任務的耗時最小,整個系統的耗時必然也是在可預測范圍內最小的。
3 分布式多機器人路徑規劃算法
結合三維空間地圖和式(2)以及帶條件DFS遍歷算法,本文提出了針對多機器人路徑規劃算法,該算法包括三維空間更新、最優路徑選擇、帶條件DFS 遍歷。在實際地圖環境下,機器人數量和任務數量沒有絕對的對應關系,一個任務的執行機器人是不確定的。在同一時刻系統不會產生多于一個任務,任務tj產生后,調度系統根據每個機器人當前時刻所處位置指派Robots集合中最符合此次任務的機器人ri完成該任務,構造一個臨時任務ttemp,其起點和終點分別是機器人ri的當前位置以及任務tj的起點,選擇最符合的機器人ri可由式(5)得出。
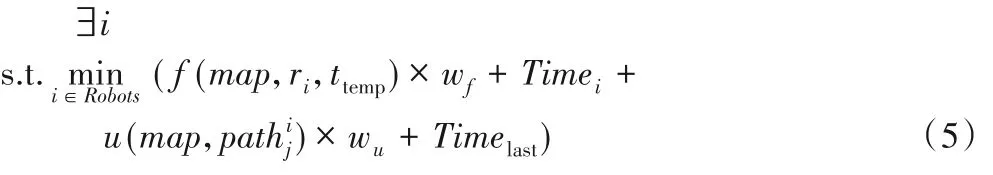
其中:Timelast表示機器人完成當前任務的剩余時間。中央控制器指派機器人ri完成任務,機器人ri必須在中央控制器更新地圖周期之內完成路徑計算,并將路徑信息發送至中央控制器,中央控制器匯總所有機器人的實時位置及機器人ri的路徑信息,并將更新后的地圖下發至每個機器人。
3.1 三維空間更新
考慮多機器人路徑規劃系統規模為a×b,時間軸z軸最大值為C,則三維時空地圖的存儲空間為a×b×C,實時三維地圖坐標系統為(x,y,z)。中央控制器按照一定的周期T更新實時地圖,該周期即是機器人移動單位長度所消耗的時間,調度系統為機器人ri指派任務tj后,必須在T時間內計算出自己的運動三維時空路徑,并將其規劃的路徑發送至中央控制模塊,如果未能在規定時間內計算完成,則需將該機器人所執行的任務插入到任務集合的尾部,等待其他任務處理完畢,再對該任務進行處理。
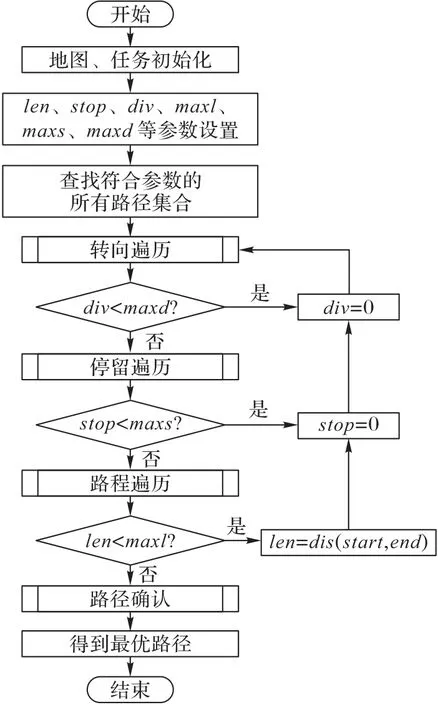
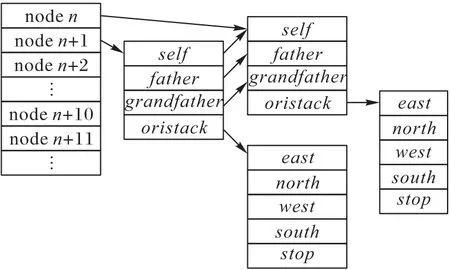
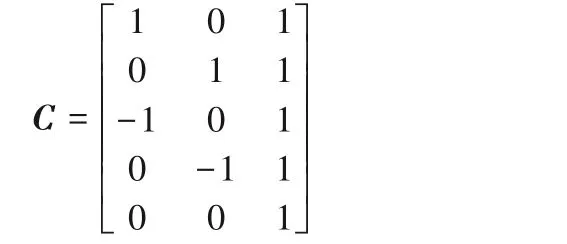
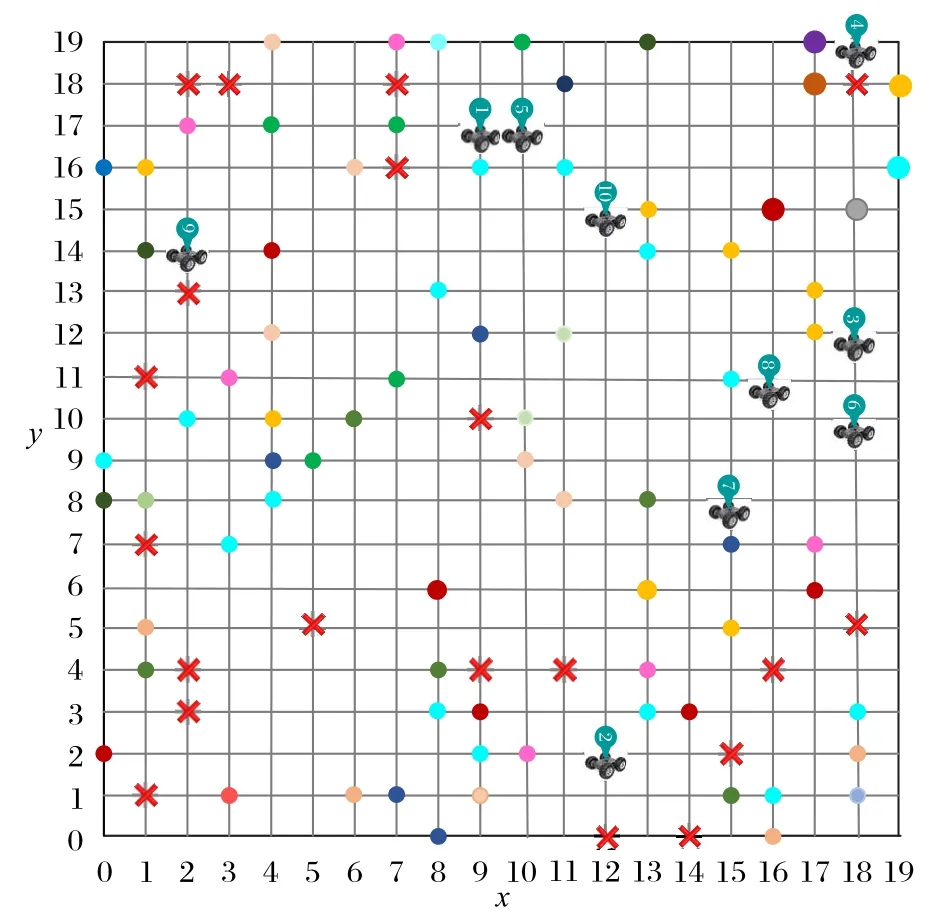
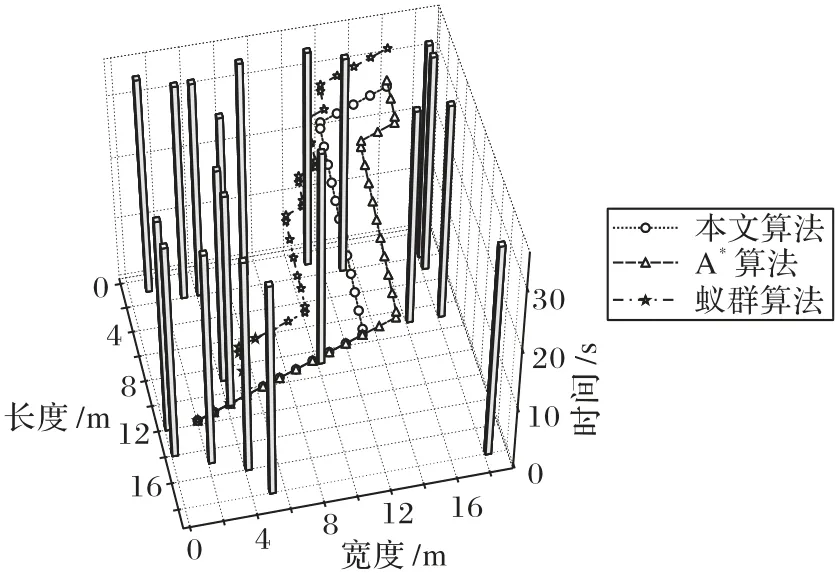
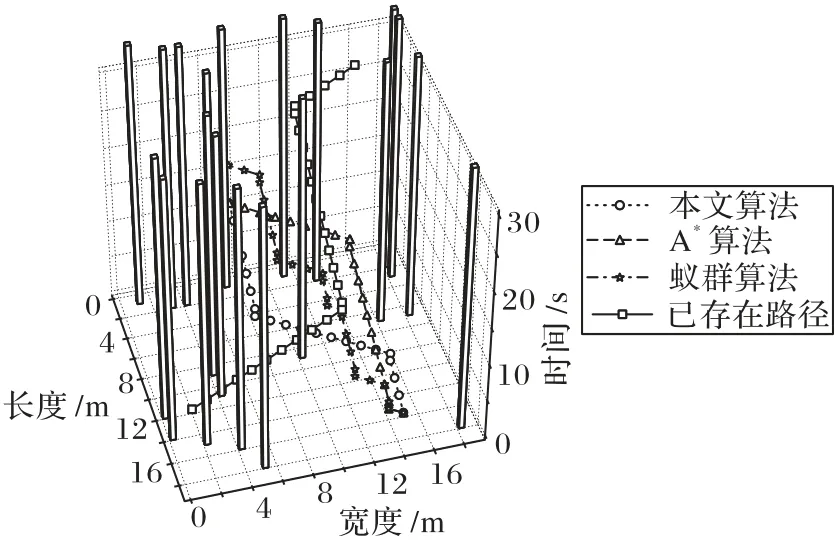
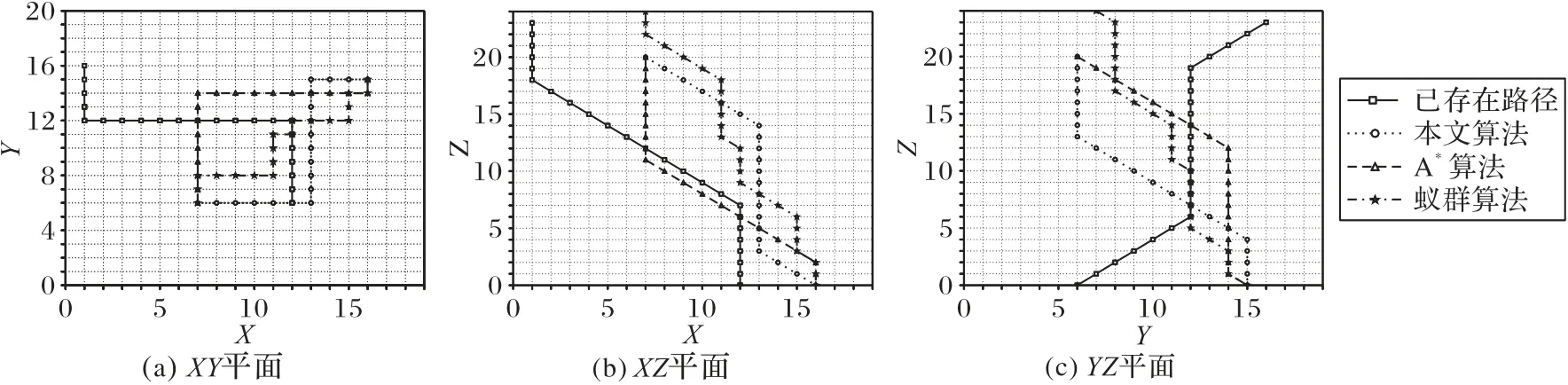
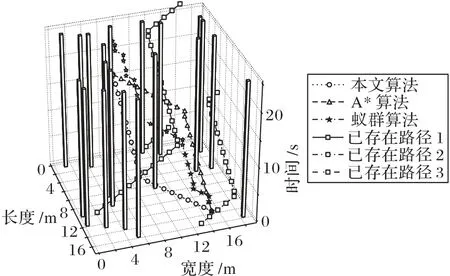
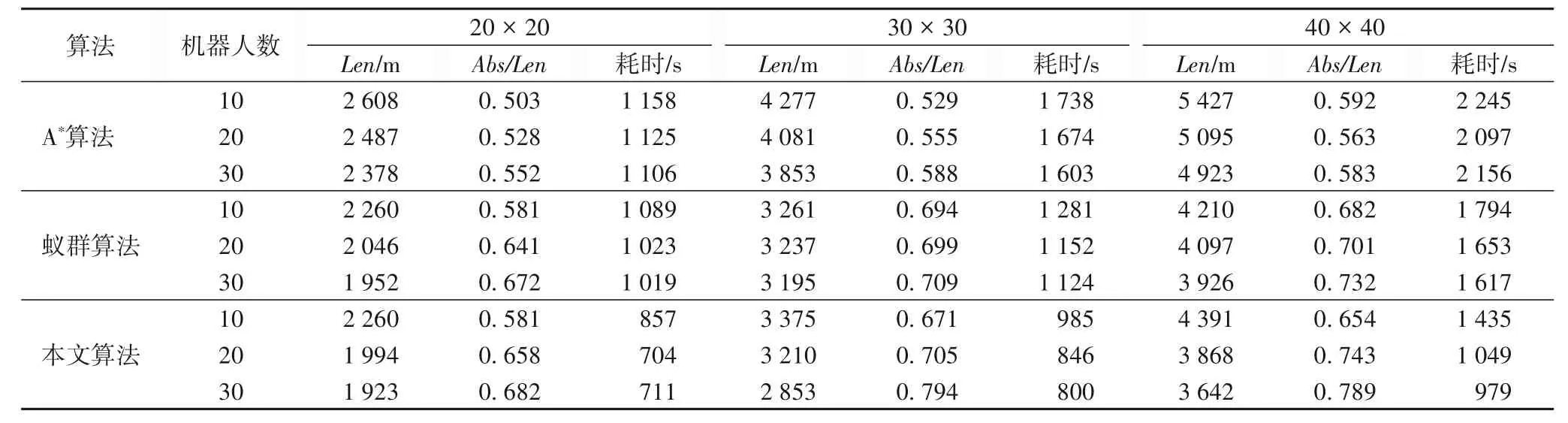
中央控制模塊更新之前需要接收n個機器人發送的實時位置信息,若實際接收到的位置信息數量n′ 不同于傳統二維柵格地圖,只是簡單地將障礙物所處位置值設置為1,三維時空地圖中除了可以表示障礙物之外,還可記錄所有機器人未來將要執行的路徑信息,消除了障礙物和路徑之間的物理性質差異,并將其統一于三維時空地圖中,降低了路徑搜索過程中算法的復雜度。三維時空地圖中某一點的值可取{0,1,…,maxR},其中,障礙物點值為maxR,無障礙物的空白處為0,而其他值的點i?{1,2,…,maxR-1}則表示機器人ri當前或者將來某一時刻所處的三維空間位置坐標,機器人ri規劃的路徑上所有節點值均為i,一次地圖更新示意圖如圖3所示。 圖3 地圖更新示意圖Fig.3 Schematic diagram of map updating 圖3中z軸表示以當前時刻為始的時間軸,圖3(a)和3(b)分別表示在宏觀時間為t和t+1的不同三維時空地圖。圖3中宏觀時間為t時刻的平面(x,z)可使用式(6)表示: 其矩陣形式可用式(7)表示: 則三維地圖更新操作可表示為: 每一次地圖更新i按{0,1,…,b-1}順序執行式(8),則機器人路徑地圖更新完畢。考慮障礙物靜態特點,三維時空地圖中的障礙物需要覆蓋整個時間軸,由于以上操作會導致三維地圖中planexyc-1=0,planexyc-1表示三維地圖中z=c-1時的(x,y)平面,即障礙物空缺問題,需要做以下處理: 其中,map(x,y,z)表示三維時空地圖中位置為(x,y)的值,x、y需要滿足如下條件:x?{0,1,…,a-1},y?{0,1,…,b-1},z=c-2,同時需滿足map(x,y,c-2)?Obstacles,Obstacles表示障礙物集合。 考慮機器人本身動態特點,機器人可以看作動態障礙物,在路徑規劃后應該在任務的終點設置臨時障礙物,即機器人本身。對于機器人ri,其步驟如下: 1)判斷機器人ri未完成的路徑長度; 2)若大于1,需要消除未完成路徑首部的動態障礙物,即map(x,y,z)=0,其中(x,y,z)滿足式(10): Research and Application of Jacket Multi-pile Structure Foundation Installation for Offshore Wind Power Engineering ZHANG Qinghai,LI Shanfeng,WANG Shuwen(126) 3)在未完成的路徑尾部設置動態障礙物,即(x,y,z)=i,其中(x,y,z)滿足式(11): 其中.start表示機器人ri執行任務tj的路徑首部;.end表示機器人ri執行任務tj的路徑尾部。 最優路徑選擇算法用于在盡可能短的時間內優先從最有可能是最優路徑的路徑集合中找出機器人執行任務的最優路徑,由于多機器人路徑規劃是NP-Hard 問題,無法在多項式時間內得到最優解,這里的盡可能短時間是指優先遍歷最有可能是最優解的路徑所需要的時間,優先遍歷的路徑可以在多項式時間內驗證該路徑是否是最優解,優先遍歷最有可能的路徑是指在給定條件下如路徑長度、轉向次數、停止次數,采用帶條件DFS 尋找解路徑,這些條件隨著遍歷路徑的數量增加而線性遞增。 初始化條件時路徑長度可由a、b兩點之間的曼哈頓距離求出,如式(12): 在給定路徑長度len、停止次數stop、轉向次數div條件下,驗證機器人ri的一條路徑是否為最優解可以通過將該路徑所需要的真實時間和完成任務tj需要的最短時間進行比較,根據式(1)只需輸入leni、pstopi、pdivi、mixi等參數,即可計算完成任務tj的最短時間。其中,混合動作mixi包含于全部原地停留次數stopi中或者全部轉向次數divi中,考慮實際多機器人系統,應該盡量減少原地停留時間,從而提高系統的運行效率。因為原地停留次數與轉向次數相比較少,故可以作mixi=(1-p)×stopi,p表示單一只是原地停止點的數量占所有停止點的數量的比例,p值較大這將減少機器人在運動過程中的混合動作,減少不必要的時間消耗。將式(1)改寫為式(13),即可將式(1)中的4個參數減少到3個。 其中:stopi是所有的原地停留次數;divi是所有的轉向次數;Td表示每次轉向所消耗的平均時間;Ts表示每次原地停止的平均時間間隔。 機器人ri按照自身計算出的路徑運動,其真實消耗時間可由路徑終點所處的z值減去起點所處的z值表示: 單個機器人路徑規劃流程如圖4 所示。通過路徑選擇算法,按照轉向參數、停止參數、路程參數依次遞增的規律,構造路徑集,在這些路徑集中可以找到一個最優路徑。該算法中各子算法步驟如下。 圖4 路徑選擇算法Fig.4 Path selection algorithm 算法1 轉向遍歷算法。 1)循環遍歷符合參數的路徑集。 2)如果路徑為空,更新div++,條件使能,終止循環。 3)如果驗證合法路徑是否是最優解計算超時,更新stop++,條件使能,終止循環。 4)如果路徑合法,結合式(2)驗證該路徑是否為最優解。 5)如果是最優解,找到最優解程序退出。 6)如果不是最優解: a)如果是首次得到路徑,設置首次路徑標志。 b)如果執行路徑耗時減a、b兩點最短耗時小于maxd,maxd=執行路徑耗時減a、b兩點最短耗時;否則,maxs=執行路徑耗時減a、b兩點最短耗時。 c)以上條件都不滿足,設置最大時間標志,保存已遍歷路徑中的最優路徑,更新div++。 3.2.2 停留遍歷 算法2 停留遍歷算法。 1)保存已遍歷路徑中的最優路徑,更新stop++。 2)如果未設置最大時間標志: a)如果轉向遍歷步驟得到的最優路徑時間小于首次路徑標志時間,最優路徑為轉向遍歷步驟得到的最優路徑,程序退出。 b)否則,最優路徑為轉向遍歷步驟中設置的首次路徑,程序退出。 3.2.3 路程遍歷 算法3 路程遍歷算法。 1)保存已遍歷路徑中的最優路徑,更新len++。 2)如果未設置最大時間標志: a)如果停留遍歷步驟得到的最優路徑時間小于首次路徑標志時間,最優路徑為停留遍歷步驟得到的最優路徑,程序退出。 b)否則,最優路徑為停留遍歷步驟中設置的首次路徑,程序退出。 3.2.4 路徑確認 算法4 路徑確認算法。 1)如果轉向遍歷步驟得到的最優路徑時間小于首次路徑標志時間,最優路徑為路程遍歷步驟得到的最優路徑,程序退出。 2)否則,最優路徑為轉向遍歷步驟得到的最優路徑,程序退出。 給定len、stop、div參數后使用DFS 搜索路徑,本文DFS 算法優先遍歷路徑集中參數符合len、stop、div的路徑情況,在地圖更新周期內找到一條路徑,則將該路徑耗時與3.2 節中的最短耗時比較,確認是否為最優路徑。 算法采用嵌套堆棧結構保存搜索內容,其結構如圖5所示。 圖5 堆棧存儲結構Fig.5 Stack storage structure 使用node 堆棧保存已遍歷過的節點,每一個節點都包含一個指針堆棧,其中存儲當前節點的自身節點self、父節點father、祖節點grandfather,可以用于判斷當前節點相對于前兩個地圖更新周期路徑是否產生了轉向或者原地停留動作,oristack表示當前節點下一步的遍歷節點堆棧,可根據實際情況設置各遍歷方向不同的入堆棧順序,規定east=4,north=3,west=2,south=1,stop=0。根據當前節點和方向堆棧棧頂元素可以計算出下一步應當遍歷的節點位置,定義矩陣: 定義函數g(i) ∈{0,1,2,3,4}表示取矩陣C的i行元素,則當前節點(x,y,z)的下一點(x′,y′,z′)可表示為: 其中i為方向堆棧上棧頂元素。 算法5 帶條件的DFS算法。 1)初始化參數。 2)將起點壓入node堆棧。 3)根據當前方向堆棧棧頂元素計算node 堆棧頂節點的下一節點。 4)計算下一節點相對于前兩個地圖更新周期的轉向數量、原地停止數量、距終點距離,如果不符合輸入參數len、stop、div,則將方向堆棧出棧,重新執行第3)步,如果方向堆棧為空,node堆棧出棧,跳轉至第3)步。 5)如果下一點是終點,找到路徑,程序退出。 6)如果下一點是障礙物,當前方向出棧,跳轉至第3)步。 7)如果下一點位置已經超出地圖范圍,當前方向出棧,跳轉至第3)步。 8)如果node 堆棧為空,表示未找到滿足當前參數條件的路徑。 通過上述帶條件DFS 算法,實現了按照路徑選擇算法中給定的參數求解相應的路徑功能,達到了符合當前參數的最短路徑要求,由于三維時空地圖中路徑搜索方向是沿著時間軸單向遞增的,最大遍歷節點為存儲空間的一半,則帶條件DFS算法的時間復雜度為(a×b×C)/2。 本文采用的實驗配置為i5-9300H CPU,8 GB 運行內存,在Windows 10 中使用Visual Studio 2019 編程進行仿真實驗,設置障礙物比例為5%。設定機器人移動單個柵格的路徑長度需要的時間為1 s。在同一地圖場景下,針對不同的障礙物比例以及不同的機器人數量,隨機產生100 個任務,其中任何一個任務可能多次出現,不同任務的起點及終點可能相同。機器人的初始位置為隨機放置,完成一次任務,調度系統將排序機器人集合中包括正在執行任務以及已經完成任務的機器人移動至任務起點的時間序列,選擇消耗時間最短的機器人為執行該任務的機器人。機器人完成當前任務后,方可執行其他任務,即從當前位置運動至新任務起點,然后開始執行新任務。 在20×20 的地圖中按其規模的5%隨機產生障礙物,如圖6 中叉點,圓點代表任務的起點和終點,其中共有50 個任務,剩下的任務重復之前的50 個任務。隨機放置10 個機器人,分布如圖6 所示。為了保證實驗的合理性以及任務多樣性,其中不同任務的起點及終點可能位于相同坐標。 圖6 實驗環境Fig.6 Experimental environment 為驗證基于三維時空地圖和運動分解的多機器人路徑規劃算法在路徑規劃方面的性能,將本文算法與A*算法[7]以及蟻群算法[10]進行對比。A*算法和蟻群算法屬于采用集中式兩層沖突消解的多機器人路徑規劃算法,其中:第一層為路徑規劃層,先為機器人分配任務,然后在忽略其他機器人影響的情況下為每個機器人規劃自己的最優路徑;第二層為沖突消解層,主要目的是消除第一層各機器人路徑之間的沖突。依據圖6 的實驗環境設置,本文算法參數設置為αi=1,βi=1,wf=0.8,wu=0.2,T=1,p=0.8。A*算法中選用曼哈頓距離表示節點距離起始節點的代價。蟻群算法參數設置為:螞蟻數量20,迭代次數200,信息素傳遞參數0.5,總的信息素1 000.0。在規劃任務t1∶start=(12,2)、end=(1,16)時,系統選擇機器人集合中完成當前任務及完成臨時任務耗時最小的機器人,由于系統初始時,機器人的當前任務皆為空,只需考慮距離第一個任務起點最近的機器人r2,路徑規劃如圖7所示。 由于機器人r10所形成的動態障礙物,本文算法規劃的路徑不能直接通過機器人r10所處位置,提前在(12,2)轉向,第二次轉向在(1,12)處,一共有兩次轉向。而A*算法首先忽略其他機器人的影響,各自規劃其路徑,其規劃的路徑會經過機器人r10、r5、r1所處位置,然后根據沖突消解算法調整路徑,最終路徑共需3次轉向。而使用蟻群算法規劃的路徑共需10次轉向。本文算法規劃的路徑真實耗時為27 s,A*算法真實耗時28 s,蟻群算法耗時為33 s。 在機器人r2,從起點運動至下一節點的時間內,系統開始規劃任務t2∶start=(16,15),end=(7,6),通過計算發現機器人r8運動至任務t2的起點耗時最短,系統將任務t2分配給機器人r8,機器人r8接收到任務后開始計算運動至任務t2起點的臨時路徑,得到計算結果后,將其計算結果上傳至中央處理模塊。當下一個地圖更新周期開始后,機器人r8將按照已規劃的路徑運動,該臨時任務的耗時為4 s,在其運動的過程中,機器人r2則獨自運動至(12,6)處。機器人r3運動至任務t2的起點后,r3將根據當前的地圖環境計算最優路徑,其規劃的路如圖8所示。 圖7 任務1不同算法路徑規劃對比Fig.7 Task 1 path planning comparison of different algorithms 其中,本文算法規劃及A*算法的路徑共有兩次轉向,完成任務2的耗時都是20 s,蟻群算法耗時為24 s。 A*算法規劃的路徑與機器人r2的運動路徑在三維空間上距離較短,即不確定性時間較長。對于計算完成任務t2的路徑在各平面的投影如圖9所示。 而蟻群算法規劃的路徑轉向次數過多,增加了機器人運動時間。 可以通過計算當前路徑與其他路徑的距離計算出不確定時間,即圖8 中三種算法規劃的路徑與已存在的路徑之間的面積。對于A*算法規劃的路徑,計算出其u(map,path32)為171,蟻群算法不確定值為234,而本文規劃的路徑不確定值為229,這意味著A*算法有更大的概率產生碰撞,從而耗費更多的時間。 圖8 任務2不同算法路徑規劃對比Fig.8 Task 2 path planning comparison of different algorithms 在計算任務t52∶start=(16,15)、end=(7,6)時,當前地圖環境中仍有正在運動的機器人,在規劃任務t52時,必須考慮到其他機器人的運動影響,通過計算發現機器人r10運動至任務t52耗時最短,系統將該任務分配給機器人r10,分別使用本文算法、A*算法以及蟻群算法計算任務t52的路徑如圖10所示。 圖9 不同算法路徑投影Fig.9 Path projections of different algorithms 圖10 任務52不同算法路徑規劃對比Fig.10 Task 52 path planning comparison of different algorithms 可以看到,A*算法規劃的路徑在(6,14)將會與機器人r3碰撞,而蟻群算法雖然不會與其他機器人發生碰撞,但是由于轉向次數過多,機器人完成任務消耗的時間也相應增多。本文算法將機器人路徑拓展至三維時空地圖后,可以在計算路徑時提前發現碰撞點,選擇其他路徑后可以避免碰撞。 地圖規模為20×20、30×30、40×40 時,任務集的總路程分別為1 312 m、2 264 m 和2 872 m,實驗對比結果如表1所示。 表1 中:Len表示機器人實際運動的路程總長度;Abs表示全部任務的起點與終點的曼哈頓距離之和;Abs/Len表示任務總長度與機器人實際運動總長度之比,其值越接近1 表示多機器人系統越高效,即機器人的空載率低,而其值越接近0 表示系統中存在過多的空載情況,效率低下。機器人實際運動路徑長度包括執行任務的路徑長度以及機器人從自身位置移動至任務起點的路徑長度。根據表1 可以看出,在障礙物比例及地圖規模相同的情況下,完成同一任務集機器人數量越多,真實路徑長度越小,總的時間消耗也是減少的。在地圖規模較小的情況下,對于完成同一任務集的機器人數量,其增加趨勢與總耗時時間的下降趨勢關系不明顯,但隨著地圖規模的增大,這種關系會更加明顯起來,即在增加相同數量的機器人情況下,地圖規模越大,系統的總耗時越少。隨著地圖規模的增大,隨機任務之間的路徑長度也會增大,這將導致系統的運行時間和真實路徑與最短路徑之比逐漸增大。 在地圖規模為20×20、30×30、40×40時,分別使用10、20、30個機器人完成100個連續任務,最終得出了本文算法與A*算法和蟻群算法相比時的總路程減少率Lper以及總耗時減少率Tper,實驗結果如表2所示。 表1 不同地圖規模下的路徑搜索代價Tab.1 Path search cost under different map scales 表2 不同地圖規模下本文算法相較于兩種對比算法的路程和時間減少率Tab.2 Distance and time reduction rate of proposed algorithm compared with two comparison algorithms under different map scales 由此可見,本文算法規劃的路徑集總長度更小,完成同一批任務耗時更短,與A*算法相比,總路程平均減少比例及總時間平均減少比例分別為21.1%、42.5%,而與蟻群算法相比,相應的總路程和總時間平均減少比例分別為2.49%、28.5%,且在地圖規模較大的場景時,這種優勢更加明顯。 本文分析了單個機器人完成特定原子任務的運動時間組成因素,將其拆分為計算機解算時間、路徑運動時間、不確定時間,并在二維柵格地圖的垂直方向拓展成時間軸,將二維地圖拓展為三維時空圖,有效地將路徑規劃中碰撞避免放在了第一層,減少了路徑沖突問題。通過具體分析路徑運動時間,將其拆分為轉向時間、原地停止時間、路徑運行時間參數,然后使用帶條件DFS 路徑搜索中優先使用低代價的參數,DFS可以在盡可能短的時間內找到一條最優路徑。本文算法與傳統算法相比系統耗時更少,并且不存在沖突情況,可以保證找到一條最優路徑,在應對突發隨機任務時更具靈活性。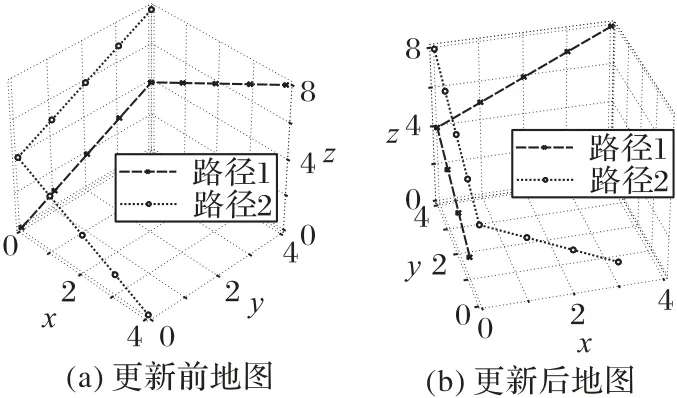
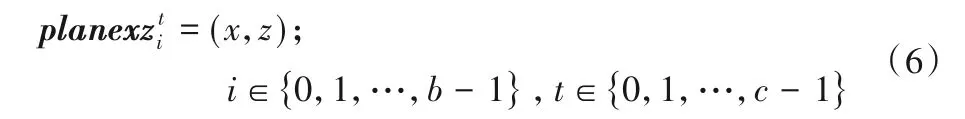

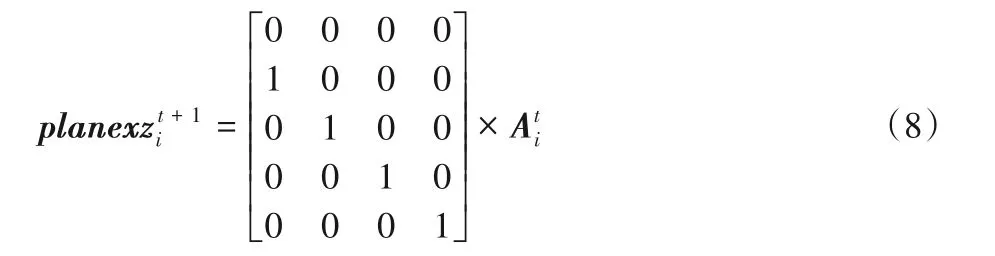
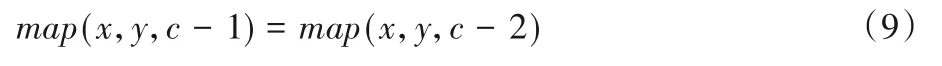

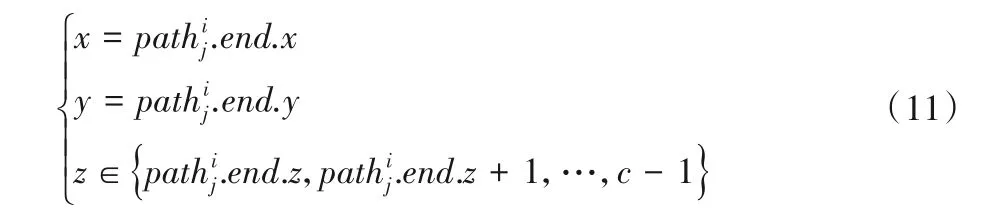
3.2 最優路徑選擇
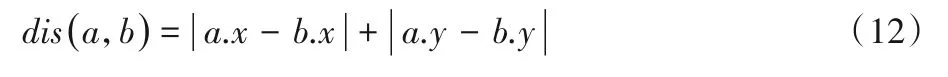
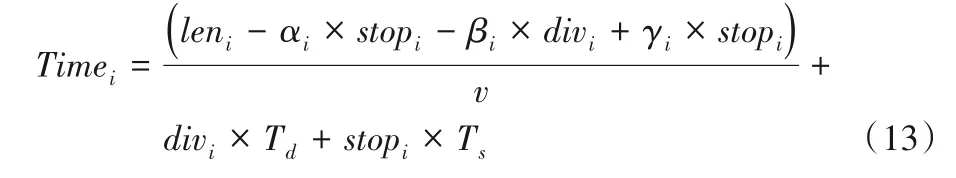
3.3 帶條件DFS遍歷

4 實驗與結果分析
4.1 實驗環境
4.2 實驗場景搭建
4.3 結果分析

5 結語

