融合標簽預處理與節點影響力的重疊社區發現算法

吳清壽，陳榮旺，余文森*，劉耿耿

（1.武夷學院數學與計算機學院，福建武夷山 354300；2.認知計算與智能信息處理福建省高校重點實驗室（武夷學院），福建武夷山 354300；3.福州大學數學與計算機科學學院，福州 350116）

（?通信作者電子郵箱45509111@qq.com）

0 引言

自然界和社會生活中廣泛存在各種網絡，如社交網絡、生物網絡、科學家合作網絡和語言學網絡等，通常將其統稱為復雜網絡。復雜網絡中，節點會依據內在規律形成緊密或稀疏的關系，進而形成社區［1］。大量研究表明，處于同一社區中的節點之間的關系比不同社區節點之間的關系更加緊密，即社區內節點的連邊稠密，而社區之間的連邊稀疏。社區發現算法研究是復雜網絡中其他研究的重要基礎工作之一，并已在社會學、物理學、流行病學、文獻計量學等領域中得到了廣泛應用［2-3］。

早期研究認為每個節點歸屬于一個社區，但真實世界網絡中，部分節點可能歸屬于多個社區，如一位科學家的研究內容可能歸屬于多個領域，這就構成了社區重疊。Palla 等［4］于2005 年提出社區重疊概念，并給出了識別重疊社區的CPM（Clique Percolation Method），其基本思想是社區內部可能存在完全圖，而社區之間的邊不會構成完全子圖。CPM 適用于稠密網絡，而大部分社交網絡是稀疏的。Zhang等［5］針對CPM的問題提出了表征弱派系相似度的方法weak-CPM，其時間復雜度降低為O（dm），d為節點平均度數，m為邊數。另外一類常用的方法是非負矩陣分解方法，Zarei等［6］提出的貝葉斯非負矩陣分解算法依賴于節點的中心性矩陣和社區度矩陣，并將社區度作為切割標準，可用于識別重疊社區和異常點。Cao等［7］提出了一種依賴于貝葉斯優化過程的混合優化算法。Zhang等［8］提出了一種基于偏好的概率非負矩陣分解（Probability Nonnegative Matrix Factorization，PNMF）模型，最大化每個節點成對偏好順序的可能性，采用隨機梯度下降引導采樣解決優化問題。胡麗瑩等［9］提出一種新的對稱非負矩陣分解算法，并用文獻［7］的方法進行重疊社區劃分。最新的研究中，Shahmoradi等［10］提出多層次重疊社區的發現方法，通過建立模型，采用遺傳算法得到初步解，再進行優化選擇以得到社區。

與本文研究相關的方法有兩類：一類是基于種子擴展的方法。Lancichinetti 等［11］提出的LFM（Local Fitness Method）以隨機節點作為種子節點，以最大化自適應函數值為目標進行局部擴展優化，可檢測層次和重疊社區，但其時間復雜度達到O（n2），且種子節點的選擇未考慮節點的重要性，算法的穩定性和適應性較差。杜航原等［12］通過搜索局部密度中心作為社區中心，提升了社區中心的發現效率。另一類方法是基于標簽傳播算法（Label Propagation Algorithm，LPA）［13］思想改進的重疊社區發現方法，代表性的算法有Coscia 等［14］提出的

DEMON（Democratic Estimate of the Modular Organization of a Network），Gregory［15］提出的COPRA（Community Overlap PRopagation Algorithm），以及Xie 等［16］提出的SLPA（Speaker listener Label Propagation Algorithm）等。DEMON 算法提取每個節點的自我網絡（ego），并在這個結構上應用LPA，再將這些局部社區進行合并，可在全局級別揭示網絡的模塊化組織，但該算法存在穩定性差的問題。COPRA 通過引入歸屬系數，將標簽傳播方法應用到重疊社區發現，其在各類網絡上具有較好的適應性，但COPRA 中標簽選擇過程隨機性較大，當社區間混合度較大時容易把整個網絡識別為一個社區。馬健等［17］對COPRA 中的節點標簽更新順序和傳播門限進行了改進，提出了COPRAPC（Community Overlap PRopagation Algorithm based on PageRank and Clustering coefficient），選擇影響力小的節點優先進行標簽傳播，并用節點聚類系數控制節點歸屬的最大社區數。SLPA 根據動態交互規則進行標簽交換，該算法在高混合度網絡中發現社區的能力較弱。

結合種子擴展和標簽傳播的思想，本文提出了一種融合標簽預處理與節點影響力（Fusing Label Preprocessing and Node Influence，FLPNI）的重疊社區發現算法，通過發現中心節點，進行標簽預處理，使得具有緊密關系的節點間具有相同的標簽，在預處理后的節點上進行標簽傳播，并以節點影響力輔助標簽選擇，降低標簽選擇的隨機性，提高算法社區發現的穩定性和準確性。

本文的主要工作如下：

1）提出了一種基于節點影響力的中心節點識別方法，利用中心節點進行標簽預處理，并能初步發現重疊節點。

2）用節點影響力輔助標簽傳播過程的標簽選擇，降低算法的隨機性。

3）引入弱社區判斷條件，以自適應函數為優化目標，對不滿足條件的社區進行合并，提升社區的內聚度。

1 相關定義

一個無權無向的復雜網絡用G=（V，E）表示，V=｛v1，v2，…，vn｝是網絡中節點的集合，E=｛e1，e2，…，en｝表示網絡中邊的集合，em=｛（vi，vj）|vi≠vj?vi，vj∈V｝。

定義1基本概念。節點vi的鄰域定義為Γi=｛vj|（vi，vj）∈E｝，vj稱為vi的鄰居節點。節點vi的度記為ki=|Γi|。

定義2內度與外度。假設C=｛c1，c2，…，cl｝是G的一次社區劃分結果，cl稱為一個社區。節點vi∈cl的內度表示vi與社區cl內部節點的連邊數量，記為(cl)。外度表示vi與社區cl外部節點的連邊數量，記為(cl)。

定義3節點影響力。用節點排名算法PageRank［18］計算節點的pr值，節點vi對應的pr值表示節點在網絡中的影響力，記為pri，其第t輪迭代的值計算公式如式（1）：

其中：Mi表示指向vi的節點集合，本文討論無向網絡，所以Mi=Γi；Lj表示vj的出度，即Li=|Γj|；N為網絡中節點數量；1-α在原算法中表示隨機跳轉到其他網頁的概率，在無向連通圖中一般不存在出鏈循環的問題，為保持與原算法的一致性，此處保留參數α，并設為0.85。

定義4中心節點。在當前節點集合中，選擇pr值最大的節點作為當前中心節點，記為cent，其形式化描述如式（2）：

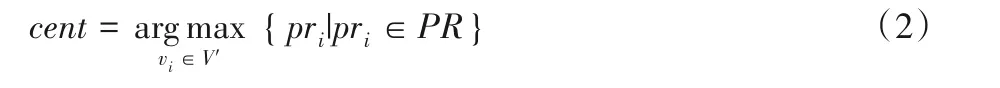
其中：V'表示當前節點集合；PR表示節點的pr值集合。

Tang 等［19］認為網絡拓撲包含兩階結構，其中二階結構考慮了節點的共同鄰居節點間的關系，若共同鄰居節點越多，則兩個節點的相似度越高。通常用公共鄰居數（Common Neighbors，CN）度量指標CN(x，y)=|Γx∩Γy|表示節點的結構相似度。本文從社區發現的角度對相似度重新定義，只對中心節點與其鄰居節點計算相似度。

定義5節點相似度。對于vj∈Γcent，節點vj與cent的相似度記為Sim（cent，vj），定義如式（3）：

當節點vj與中心節點cent無其他的共同鄰居節點時，|Γcent∩Γj|的值為0。為避免鄰居節點相似度為0 的情況，在式（3）中，對分子式加1。vj可能與多個中心節點相鄰，設分母為|Γj|，可衡量vj與不同中心節點的相似度，有利于發現重疊節點。

定義6同質節點與異質節點。當Sim（cent，vj）>δ時，稱節點vj與中心節點cent同質，否則稱節點vj與cent異質。

若vj與中心節點同質，則其擁有中心節點的標簽，與多個中心節點同質，就可同時擁有多個標簽。

定義7標簽預處理規則。對于已按pr值非升序排列的節點列表V'，逐個選擇中心節點cent，將cent的標簽賦予同質的節點。若滿足Rj≥1/γ，則vj保留在V'中；否則將vj從V'中刪除。其中，Rj=Rj-Sim（cent，vj），Rj的初值為1。循環這個過程，直到V'=?。

各類標簽傳播算法中，一般情況下，同步標簽傳播的穩定性和收斂性高于異步標簽傳播，本文也采用相同方法。同步標簽傳播中，t時刻vi的標簽由t-1時刻節點vi鄰居節點的標簽分布決定。

定義8標簽隸屬系數。標簽隸屬系數記為bct（l，i），表示t時刻節點vi的標簽為l的概率。bct（l，i）定義為：

定義9標簽傳播規則。對于l∈LBK：若bct（l，i）≥1/γ，將l加入vi的標簽集合lbi中，lbi=lbi∪l；否則，設置lbi=lbmaxl，maxl定義如式（5）：

其中：γ是節點可能歸屬的最大社區數；表示節點i的鄰居節點中標簽為l的節點集合；LBK表示Γi中所有節點的標簽集合。標簽傳播中的第一步根據標簽隸屬系數可以找到節點可能擁有的多個標簽，第二步融合節點影響力的標簽傳播可以提高算法的穩定性。

當網絡社區之間的混合度較小時，經標簽傳播后的社區一般無需合并。混合度較大時，可能會形成部分不符合弱社區定義［20］的社區，此時需要將這類社區與其相鄰社區進行合并。本文采用自適應函數［11］作為合并目標社區的判斷依據。

定義10弱社區。當社區內所有節點內度之和大于其外度之和，稱該社區為弱社區。即弱社區c應滿足式（6）：

系數θ的默認值取1，對于混合度較大的網絡，隨著μ值增大而適當調整θ的取值將會得到更為合理的社區劃分。

定義11自適應函數。自適應函數記為f（c），定義如式（7）：

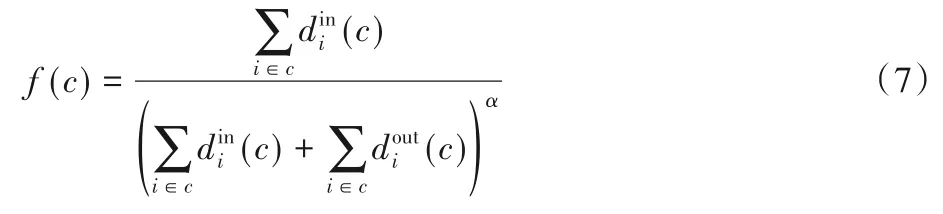
其中，α是社區規模控制參數，其取值一般為0.8～1.2。同一社區內的節點內度之和越大，則f（c）值越大，社區的內聚度越高。

2 FLPNI算法

FLPNI 算法包含標簽預處理、重疊社區發現和優化處理三個步驟，其流程如圖1所示。

1）節點標簽預處理階段。社交網絡中，同一社區中相鄰的兩個節點之間，節點的影響力值越大，則其向另一節點傳播標簽的概率越大［21］。首先計算全部節點的pr值，選取pr值最大的節點作為中心節點，并用中心節點的標簽對同質節點進行標簽預處理。當中心節點對同質節點的標簽傳播完成后，將不可能歸屬于多個社區的節點從待處理節點集合中刪除。之后，從待處理節點集合中再次選pr值最大的節點作為下一個中心節點，用同樣的方法進行鄰居節點標簽預處理。重復上述過程，直到待處理節點集合為空。經過標簽預處理，初始標簽數量將大量減少，有利于后續的標簽傳播。

圖1 FLPNI算法流程Fig.1 Flow chart of FLPNI algorithm

2）重疊社區發現階段。采用標簽傳播的方式進行節點標簽選擇，計算節點的標簽隸屬系數，識別出重疊節點。對于非重疊節點，根據節點的影響力進行標簽選擇。此措施可提高標簽選擇的穩定性和準確性。

3）優化處理階段。對于社區間混合度較高的網絡，標簽傳播結束后會產生一些不符合弱社區條件的社區，需要將其與其他社區合并。用自適應函數增量最大化選擇合并的目的社區，可以提高社區內聚度。

2.1 算法偽碼

由算法模型及相關定義，FLPNI 算法的偽代碼如算法1～算法3所示。

算法1 中引入節點與中心節點的剩余相似度Ri，其初值為1，該值用于控制節點vi可歸屬于哪些社區以及何時從待處理節點列表中刪除。

經過標簽預處理，相似度高的節點間具有相同的標簽，標簽總體數量大幅度減少，降低了后續標簽傳播的隨機性，且在此過程中將發現部分重疊節點。

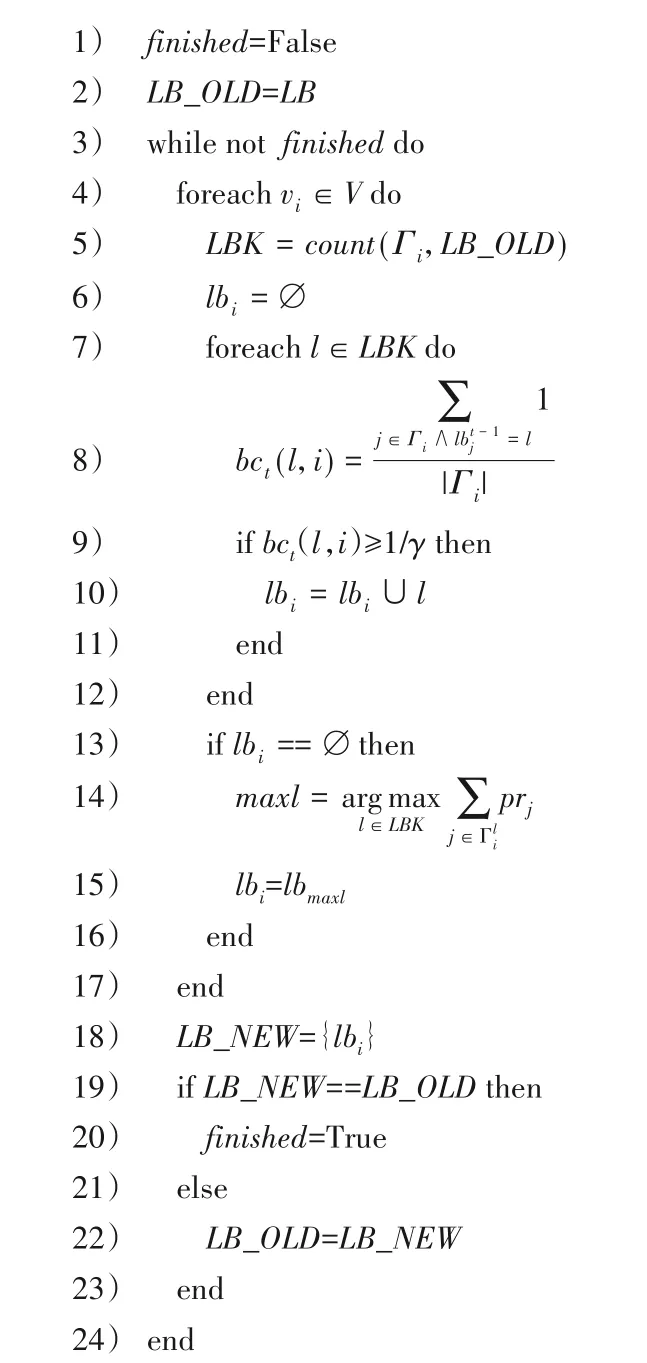
算法2根據定義9進行處理，其中選擇節點pr值之和最大的標簽作為當前節點標簽的措施，減少了選擇標簽的不確定性，并提高算法的精確度。

算法3 對社區進行合并，合并后的社區具有更大的內聚度，社區結構更加健壯。其中Update()方法用于社區更新和重疊節點標簽的處理。

以圖2 為例，對FLPNI 算法的操作過程進行描述，具體步驟如下：

步驟一 圖2（a）是網絡的初始狀態。根據Pagerank 算法，計算圖2（a）中各節點的pr值。為了說明問題，此處按pr值降序將對應節點排名，得到節點序列V'={5，11，7，13，12，0，1，2，6，4，14，10，15，3，8，9}。從V'中選擇pr值最大的節點v5為第一個中心節點。對于v5的鄰居節點，若Sim（v5，vj）≥δ，即節點與v5屬于同質節點，則用v5的標簽預處理鄰居節點的標簽。其中，節點｛4，6，7，8，9｝與v5都是同質節點，經標簽預處理，形成候選社區c1=｛4，5，6，7，8，9｝。

此時有兩種情況：

1）用于非重疊社區檢測時，直接將以上節點從V'中刪除，得到V'={11，13，12，0，1，2，14，10，15，3}。

2）對于重疊社區，需要進一步計算。若與中心節點的相似度滿足Rj≥1/γ，說明vj還可能歸屬于其他社區，則節點vj不能刪除。所以，對c1中的節點，從V'中刪除除v7外的其他節點，得到V'={11，7，13，12，0，1，2，14，10，15，3}。

不管是上述哪種情況，此時從V'中選擇第一個節點v11（pr值最大）作為下一個中心節點。重復步驟一，直到V'=?。

最終形成4 個中心節點及其預處理后的鄰居節點標簽，可看成候選社區：c1=｛5，4，6，7，8，9｝，c2=｛11，7，10，12，13，15｝，c3=｛0，1，2，3｝，c4=｛14｝，候選社區中的第一個節點為當前社區的中心節點。經過預處理，節點v7已同時擁有兩個標簽v7：｛lb5，lb11｝。結果如圖2（b），此時網絡節點的標簽數量大量減少。

步驟二 在圖2（b）的基礎上，計算節點的標簽隸屬系數，對于隸屬度大于等于1/γ的標簽直接保留，此時可進一步識別出重疊節點。如節點v4，設γ=3，其標簽隸屬系數為bc(lb0，4)=1/3，bc（lb11，4）=1/6和bc（lb5，4）=1/2，可保留兩個標簽v4：｛lb0，lb5｝，而當γ=2 時，則只保留標簽v4：｛lb5｝。對于v7，當γ≥2時保留兩個標簽，而當γ=1時，其鄰居節點中標簽l5對應的節點為v4和v5，標簽l11對應的節點為v11和v15，計算標簽對應節點的pr值之和，pr4+pr5>pr11+pr15，所以選擇v7的標簽為lb5。經過迭代傳播，直到節點標簽不再發生變化。結果如圖2（c）。

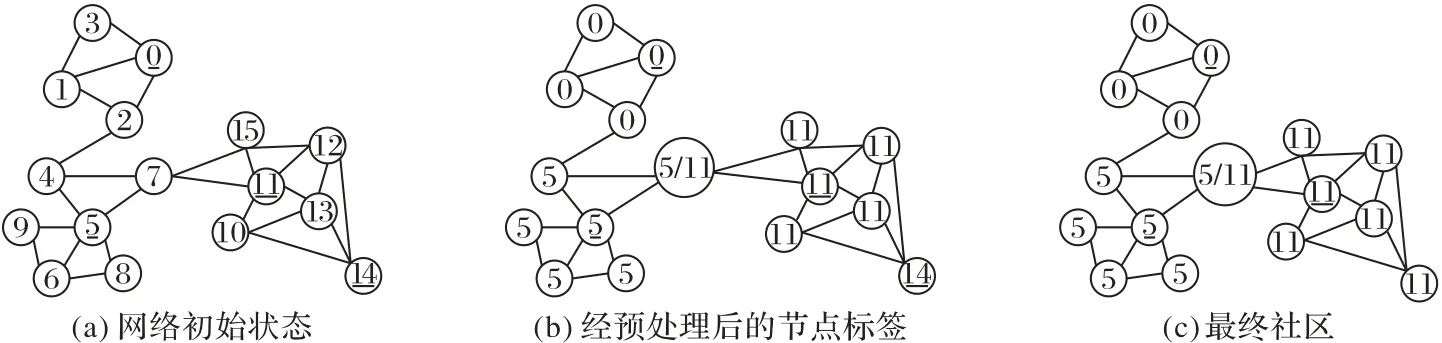
圖2 FLPNI算法模型Fig.2 FLPNI algorithm model

步驟三 對于步驟二得到的社區，進行弱社區判斷，對不滿足弱社區定義的，選擇合并后自適應函數增量最大的社區進行合并。圖2（c）中的社區都滿足弱社區，無需合并，算法結束。

2.2 算法時間復雜度分析

約定網絡節點的數量為n，邊的數量為m，節點的平均度為k=2m/n，重疊節點數量on，節點歸屬的最大社區數為γ。

1）標簽預處理。用PageRank 算法計算節點pr值的時間復雜度為O（n+m）［22］，將節點按pr值排序的時間復雜度為O(nlogn)。求中心節點與單個鄰居節點相似度的時間復雜度為O（k）。因為大部分節點都只與一個中心節點相連，共需要對n+on個節點計算相似度，計算全部節點與候選核心節點相似度的時間復雜度為O（k（n+on）），on值一般較小，可以忽略，則可簡化為O（kn）。從V'中刪除已進行標簽預處理的節點的時間復雜度為O（n）。所以，標簽預處理函數的時間復雜度為O(n+m+nlogn+kn+n)，又因為k=2m/n，標簽預處理階段的時間復雜度可表示為O(m+nlogn)。

2）重疊社區發現。進行標簽傳播的過程與COPRA 相似，對于一個稀疏網絡，每次迭代的時間復雜度為O(γ3n+γnlogγ)，通常情況下γ是一個很小的值，所以每次迭代的時間復雜度接近線性。實驗中，迭代次數一般小于10。此過程中增加了節點pr值輔助判斷標簽歸屬，不會增加算法的時間復雜度。

3）優化處理。首先計算社區是否滿足弱社區條件，需要對每個節點的鄰居節點查詢其歸屬社區，其時間開銷為O(kn)。計算f（c）同樣需要查詢節點及鄰居節點的社區分布，且只在不滿足弱社區條件的情況下執行，所以其時間開銷不超過O（kn）。

綜上，FLPNI 算法的三個步驟都具有接近線性的時間復雜度，算法總體時間復雜度為O(m+nlogn)。

3 實驗與結果分析

本文實驗包含了7 個對比算法，并分別在真實社交網絡和LFR（Lancichinetti-Fortunato-Radicchi）人工基準網絡進行實驗。對于有真實社區劃分的網絡，采用標準化互信息（Normalized Mutual Information，NMI）指標［23］進行對比評價。對于真實網絡，大部分情況下無法獲取其社區劃分，目前主流的方法是采用擴展模塊度（Extended modularity，EQ）函數［24］進行評價。實驗環境為：Intel Core i7-8650U CPU 4.10 GHz，16 GB內存，Windows 10操作系統，算法采用Python3.7實現。

對比算法包括COPRA、DBLINK（Density-Based LINK）［25］、CPM、LFM、DEMON、SLPA 和COPRAPC［17］。對比算法的參數設置如下：DBLINK 中，設置參數u=2～4，ε=0.1～0.4，步長設置為0.02。CPM 中，設置參數k=3～10。LFM 中，設置參數α=0.8～1.2。DEMON 中，設置參數ε=0.1～1。在SLPA 中，迭代次數設置為15，參數r=0.1～0.5。COPRA 中，參數v=2～9。各算法在參數范圍內評價指標均達到最大值。考慮到算法隨機性對結果的影響，FLPNI、COPRA、DEMON、LFM、COPRAPC和SLPA各運行15次，并取各次最大值的平均值。

3.1 實驗數據集

3.1.1 真實網絡數據集

實驗涉及的真實網絡數據集包含PGP（Pretty Good Privacy）［26］、Football、Karate、Polblog、Jazz 和Dolphins。其中，后面五個數據集來自于網站http：//www-personal.umich.edu/～mejn/netdata/。各個網絡的節點數和邊數情況如表1所示。

表1 真實網絡信息Tab.1 Information of real networks

3.1.2 LFR人工基準網絡

LFR 人工基準網絡［27］的各參數意義如下：N是生成網絡的總節點數；minc和maxc規定一個社區中節點的最小和最大數量；k和maxk表示節點的平均度和最大度；μ是混合度參數，用于表示社區的清晰度，其值越大，各社區間的連接邊數越多，結構越不清晰，社區發現的難度越大。μ是衡量算法穩定性的一個重要指標。重疊社區中，on表示網絡中具有重疊社區的節點數量，om表示節點最大可歸屬的社區數。本文實驗數據集的各參數值設定如表2 所示。其中，全部網絡的節點度冪率分布指數τ1=2，社區規模冪率分布指數τ2=1。

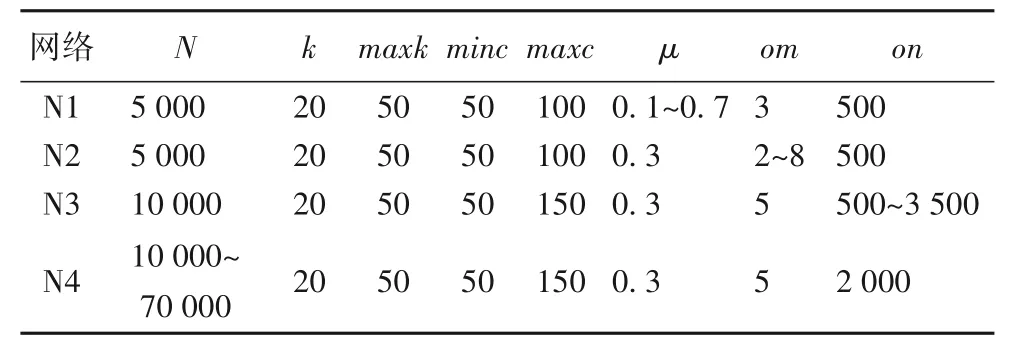
表2 LFR基準網絡信息Tab.2 Information of LFR benchmark networks

3.2 評價指標

用于實驗的評價指標包括EQ和NMI。

3.2.1 重疊模塊度

本文研究的對象為重疊社區，所以對于無真實社區劃分的網絡，算法運行結果采用EQ指標作為重疊社區結構劃分質量的評價指標。與Girvan 等［1］提出的模塊度指標不同的是，EQ中增加了節點歸屬社區數因子，定義如下：

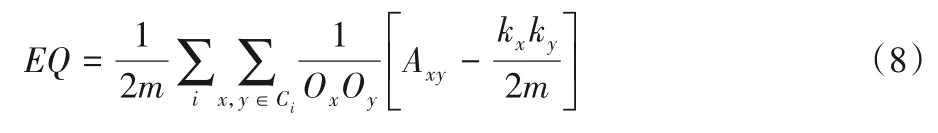
其中：Ci表示算法劃分得到的第i個社區；Ox表示節點x歸屬的社區數；A是鄰接矩陣，節點x和y是鄰居節點時Axy=1，否則Axy=0；kx是節點x的度；m是網絡邊數。

3.2.2 標準化互信息

對于具有真實社區劃分的網絡，可采用NMI指標對算法運行結果予以評價。NMI用于比較基準網絡社區結構與算法所獲取社區結構的相似程度，其定義如下：

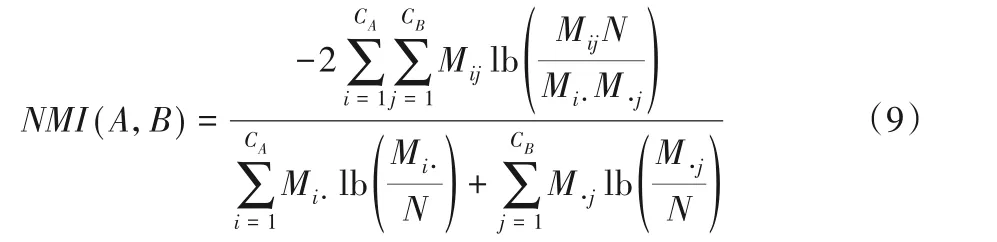
其中：A是真實社區結構；B是算法劃分結果；N是節點數；M是混淆矩陣；CA是真實社區數量；CB是經算法劃分得到的社區數量；Mi·是A中第i個社區的節點數，即矩陣M中第i行元素之和；相應地，M·j表示B中第j個社區的節點數，即矩陣M中第j列元素之和；Mij表示A中第i個社區的節點屬于B中第j個社區的節點數。NMI的值域為［0，1］，值越大則表示算法的效果越好，當NMI（A，B）=1時，表示A和B的結構完全相同。

3.3 參數的取值實驗

FLPNI 算法中涉及三個參數α、δ和γ。自適應函數fitness中的參數α建議取值范圍為0.8～1.2，本文設置α=1。參數δ和γ的取值討論如下。

3.3.1δ的取值實驗

在標簽預處理階段，需要判斷中心節點與鄰居節點是否同質，參數δ的取值與μ的關系較大，因此，本實驗在具有不同μ值的N1數據集上進行，實驗結果如圖3所示。

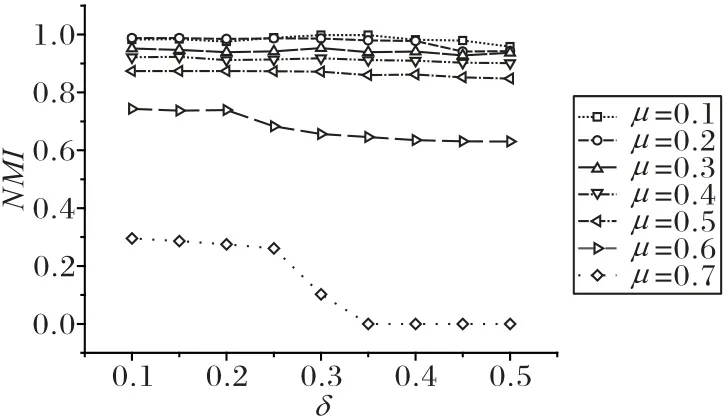
圖3 參數δ實驗結果Fig.3 Experimental results of parameter δ

對于μ≤0.5 的網絡，δ的變化對結果影響較小。其中，各個數據集在δ=0.3 時會取得較優的結果。對于μ=0.6 的數據集，當δ>0.2，NMI的下降比較明顯，且NMI值隨著δ值的增大而呈下降趨勢。在μ=0.7 的數據集上，當δ>0.3 時，FLPNI 算法得到的NMI值為0，即把整個網絡劃分為一個社區。可見，在μ較小的網絡中，同一社區的節點間關系較為密切，δ的取值變化對結果影響小。在μ較大的網絡中，節點間的相似度較小，當δ值較大時，無法識別同質節點，沒有達到標簽預處理的目的，導致在μ=0.7的數據集上，將整個網絡識別為一個社區，其結果與COPRA 相同。所以，建議在μ≤0.4 時，設δ=0.3；μ=0.5時，δ設為0.2～0.25；μ≥0.6時，δ設為0.1～0.15。

3.3.2γ的取值實驗

γ用于控制節點在多大概率上可以接受鄰居節點的標簽傳播，其值越大，節點可能歸屬的社區數就越多。而一個節點歸屬的社區情況通常是未知的，并不是歸屬的社區數越多越好。圖4是在N1上γ的取值實驗結果。

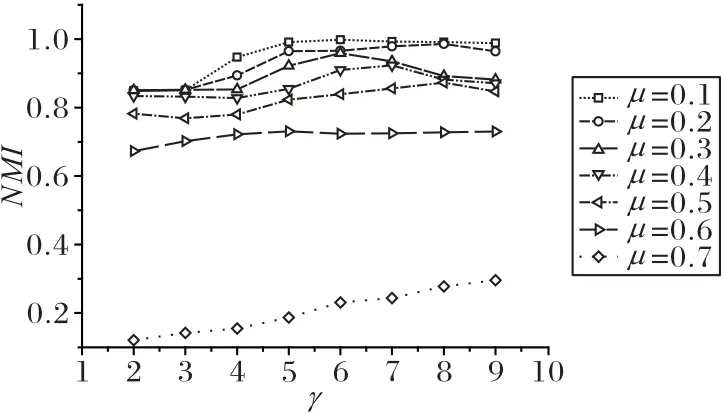
圖4 參數γ實驗結果Fig.4 Experimental results of parameter γ

對于μ≤0.4的網絡，γ=6～7時FLPNI算法得到的NMI值最大。對于μ≥0.5 的網絡，算法得到的NMI值呈現隨γ值增加而增大的趨勢。這是因為μ值越大，歸屬于其他社區的鄰居節點就越多，節點的標簽隸屬度變小。當γ值較小的時候，節點歸屬的社區數就少，易將重疊節點誤判為只歸屬于一個社區，算法得到的社區劃分結果與實際情況差別較大，造成NMI下降。

3.4 在真實網絡上的實驗結果分析

FLPNI 算法與其他7 個對比算法在Karate 等6 個真實網絡上的實驗結果如圖5 所示。在Polbooks、Dolphins 和PGP 三個網絡上，FLPNI 算法的社區劃分結果EQ值最大。在Football網絡上的實驗結果中，SLPA 具有最大的EQ值，FLPNI與LFM 的結果相同，高于其他算法。在Karate 網絡上，FLPNI算法得到的EQ值小于LFM 算法，但其得到的結果與真實社區劃分一致。除Jazz 網絡之外，FLPNI 算法在其他網絡上得到的社區劃分結果其EQ值都優于COPRA，表明融合標簽預處理和節點重要性的方法對提高標簽傳播的準確性是有效的。

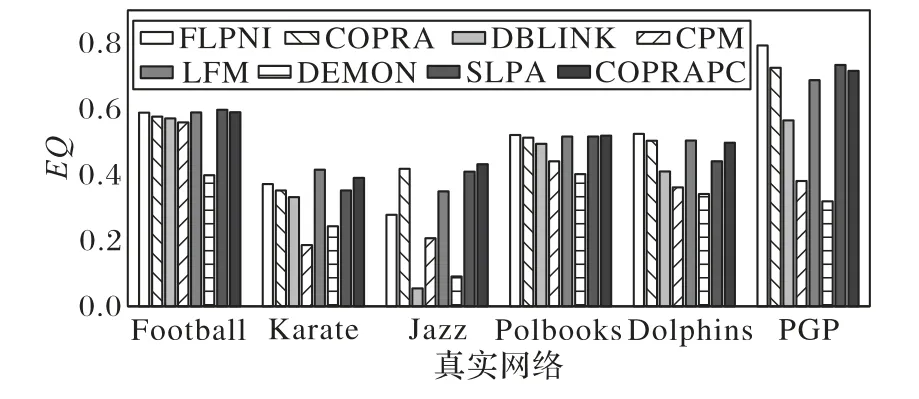
圖5 真實網絡上不同算法的實驗結果（EQ值）Fig.5 Experimental results of different algorithms on real networks（EQ value）

3.5 在LFR基準網絡上的實驗結果分析

將本文算法和對比算法在LFR 基準網絡（表2）上進行實驗，分別檢測算法對于混合度參數、節點歸屬社區數和網絡中重疊節點數量變化的適應性。

3.5.1 在不同μ值網絡上的精度實驗

對于表2 中的N1 數據集，各算法劃分出的社區的NMI值如圖6所示。

隨著μ值增加，各算法得到的NMI值都呈下降趨勢。其中，FLPNI 算法在7 個網絡上的NMI值都高于對比算法。FLPNI 算法在第一步進行了標簽預處理，形成了初步的社區，有效解決了高混合度網絡中標簽傳播隨機性大的缺陷，其在μ=0.7 的網絡中仍可以把部分節點劃分到正確的社區中；而其他對比算法得到的NMI值等于0 或接近0，且由表3 可知，COPRA 和COPRAPC 得到的社區數為1，已無法識別社區，這是μ值過大、標簽過度傳播引起的結果。

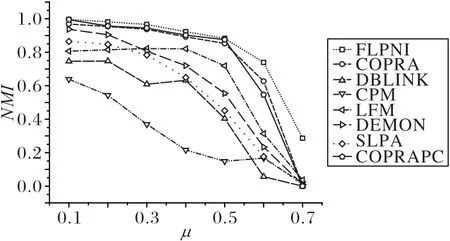
圖6 不同μ值網絡上的精度實驗結果Fig.6 Experimental results of accuracy on networks with differentμ

3.5.2 在不同om值網絡上的精度實驗

在不同om值網絡（N2網絡）上的實驗結果如圖7所示。

圖7結果表明，對于不同的om值，FLPNI算法都具有較強的適應性，其得到的NMI值均高于對比算法。FLPNI 算法在網絡優化處理階段對部分不滿足弱社區定義的待合并社區進行了優化處理，基于自適應函數的處理方法增強了社區的內聚度，提高了社區發現的質量。

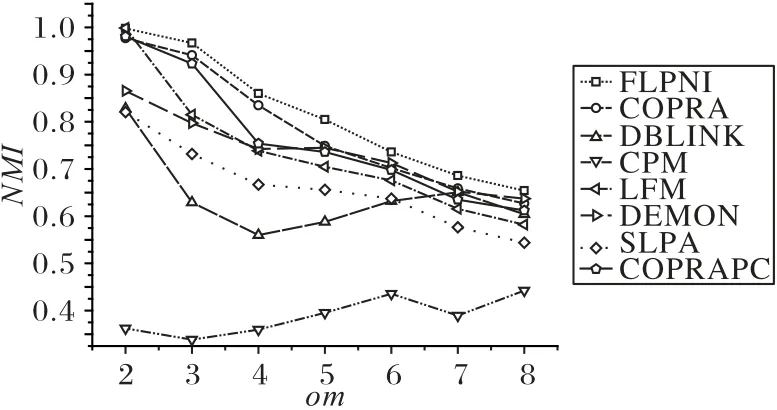
圖7 不同om值網絡上的精度實驗結果Fig.7 Experimental results of accuracy on networks with different om

3.5.3 在不同on值網絡上的精度實驗

在不同on值網絡（N3 網絡）上的精度實驗結果如圖8所示。

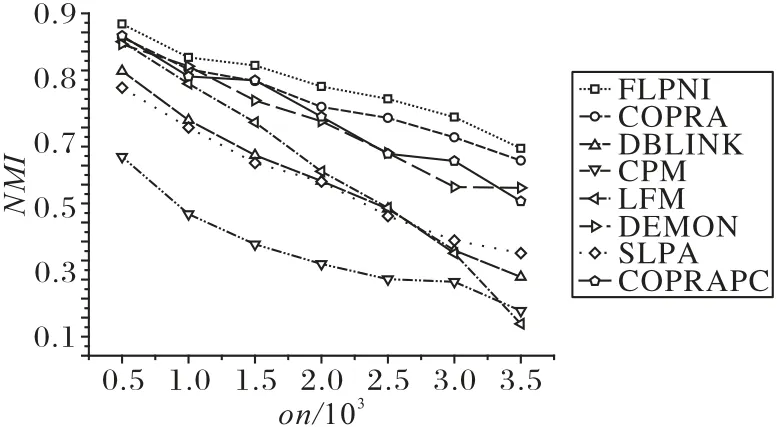
圖8 不同on值網絡上的精度實驗結果Fig.8 Experimental results of accuracy on networks with different on

隨著網絡中重疊節點數量增加，社區發現難度逐漸變大。當on=3 000 時，LFM、CPM 和DBLINK 算法得到的NMI值小于0.3，發現的社區質量較差；當on=3 500 時，LFM 和CPM 的NMI值接近0，已無法識別社區。FLPNI、COPRA、COPRAPC和DEMON 算法具有較好的適應性。在8 個算法中，FLPNI 算法仍然具有最大的NMI值。

3.5.4 在不同規模網絡上的時間性能實驗

在不同規模網絡（N4 網絡）上的時間性能實驗如圖9所示。

圖9 在不同規模網絡上的時間性能實驗結果Fig.9 Experimental results of time performance on networks with different scales

其中，SLPA具有最快的運行速度，DBLINK的運行時間比SLPA 略長。FLPNI、COPRA 和COPRAPC 的時間性能較為接近，FLPNI 運行時間略長于COPRA，主要原因是FLPNI 中，經標簽預處理后，標簽傳播的迭代次數減少，但前期預處理的時間復雜度為O(m+nlogn)，當網絡規模增大時，其運行時間會比COPRA 有所增加。FLPNI 算法的時間性能明顯優于LFM、CPM 和DEMON 等三個算法。實驗結果表明，FLPNI 算法具有接近線性的時間復雜度。

3.5.5 算法得到的社區數量

算法得到的社區數量與真實社區數量的接近程度，可以作為輔助衡量算法社區發現能力的一個指標。對各類算法在N1數據集上發現的社區數量進行比較，實驗結果如表3所示，其中NCREAL表示網絡的真實社區數。在μ≤0.5 的網絡上，FLPNI 算法得到的社區數與真實社區數一致。COPRA 得到的結果也比較接近真實社區數量，但其和DBLINK 算法在μ=0.7 的網絡上無法檢測社區，將整個網絡識別為一個社區。CPM 和LFM 識別出的社區數與真實情況差別較大，其對應的NMI值也趨于0。實驗結果表明，本文算法劃分的社區數更接近真實社區數量。

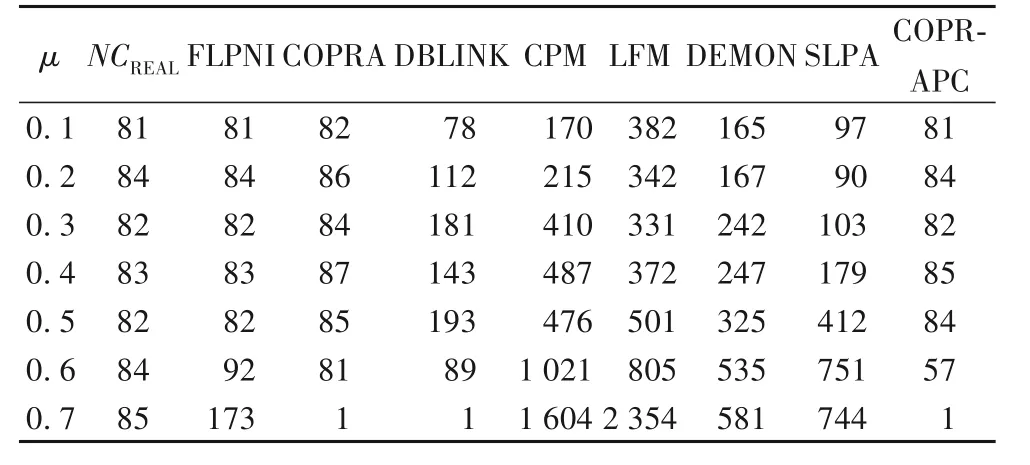
表3 不同算法劃分的社區數Tab.3 Number of communities detected by different algorithms

4 結語

本文提出了一種融合標簽預處理和節點影響力的重疊社區發現算法。該算法針對初始階段節點標簽傳播隨機性較大的問題，利用節點重要性排名，提出了一種中心節點識別方法，并利用中心節點對鄰居節點進行標簽預處理，同時根據剩余相似度識別出與多個中心節點有緊密聯系的重疊節點。經過預處理，相似度較高的節點具有相同的標簽，標簽數量大幅度減少，降低了后續標簽傳播的隨機性和迭代次數。在重疊社區發現過程，對于非重疊節點，在需要隨機選擇標簽的情況下，對鄰居節點按標簽分組計算對應節點的影響力作為選擇標準，減少了標簽震蕩現象，提高了算法的穩定性和社區劃分的精確度。最后，通過計算社區內節點的內度與外度分布，以優化內聚度為目標，將內度較小的社區與相鄰社區合并，提高了社區質量，且使得算法得到的社區數量與真實社區數量較為接近。通過與其他算法在真實網絡和人工網絡上的實驗結果對比，驗證了所提出算法的有效性。

下一步的研究中，一個改進的方向是在動態網絡中快速識別中心節點，使得算法可以擴展應用于動態網絡的重疊社區識別。針對大規模網絡，還需要考慮將關鍵步驟并行化，進一步提高算法效率，以適應規模日益增長的社交網絡應用。