運用分球入盒模型巧解隨機取數問題

高珊

運用分球入盒模型巧解隨機取數問題

高珊

（阜陽師范大學 數學與統計學院，安徽 阜陽 236037）

分球入盒和隨機取數是概率論中2個重要的古典概型，隨機取數模型往往可以轉化為分球入盒模型．通過舉例說明分球入盒模型在隨機取數問題中的妙用之處．該方法形象直觀，便于學生理解，有利于提高教學效果，激發學生學習興趣．

分球入盒；隨機取數；概率問題

分球入盒模型和隨機取數模型[1-6]是概率論古典概型中2種常見的模型．教師在概率統計的教學中要不斷地融入數學建模的思想[7]．到目前為止，許多專家學者從不同角度對分球入盒模型和隨機取數模型進行了大量的研究[8-10]．很多場合下，隨機取數問題都可以轉化為分球入盒模型進行求解，如果能夠巧妙地將隨機取數問題轉化為分球入盒問題，那么復雜難求的隨機取數問題就會迎刃而解．在教學過程中，如果教師可以引導學生巧妙利用轉化和類比的思想，不僅可以加深對原問題的理解，而且可以發散學生思維，激發學生興趣．本文結合具體實例展開關于妙用分球入盒模型，巧解隨機取數問題的探析．

1 隨機取數模型及其轉化的分球入盒模型

表1 隨機取數模型

對于分球入盒模型可得到表2．

表2　分球入盒模型

為分析問題的需要，給出關于分球入盒的古典概率問題相關結論．

2 妙用分球入盒巧解隨機取數問題舉例

例1 從1，2，3，4這4個數字中有放回隨機逐個取數：

例１可以不用轉化為分球入盒問題，但相對分析較復雜[2]40．

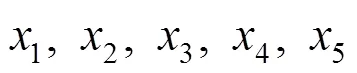
例2通過將事件“總和為20”的樣本點個數轉化為分球入盒問題而得到巧妙解決，顯示出轉化思想的重要性．文獻[2]利用母函數的方法給出求解．對于大學生或中學生來講，本題解法更加巧妙．

3　結束語

本文介紹了古典概型中的2大常用模型——隨機取數模型和分球入盒模型．通過把隨機取數模型轉化為分球入盒模型，使得較為復雜的有關隨機取數問題得到了巧妙的解決．本方法在概率統計教學中非常值得推薦，利用歸類和類比的方法把看似不同的問題轉化為同一問題，能夠讓學生體會概率論學科的美妙之處，并能激發學生的學習興趣，增強其學習滿足感．

[1] 茆詩松，程依明，濮曉龍．概率論與數理統計教程[M]．北京：高等教育出版社，2011

[2] 孫榮恒．趣味隨機問題[M]．北京：科學出版社，2015

[3] 威廉費勒．概率論及其應用[M]．胡迪鶴，譯．北京：人民郵電出版社，2006

[4] 曹振華，趙平，胡躍清．概率論與數理統計[M]．南京：東南大學出版社，2002

[5] 魏宗舒．概率論與數理統計教程[M]．北京：高等教育出版社，2010

[6] 盛驟，謝式錢，潘承毅．概率論與數理統計[M]．北京：高等教育出版社，2018

[7] 李曉毅，徐兆棣．概率統計教學與數學建模思想的融入[J]．沈陽師范大學學報：自然科學版，2008，26（2）：245-247

[8] 馬永梅．一道摸球問題的猜想證明及延伸[J]．廊坊師范學院學報，2012，12（3）： 5-7，14

[9] 周國平．一種“分球”概率的計算方法[J]．杭州師范學院學報，2003，2（4）：23-25

[10] 李永紅．古典概率中的一個問題[J]．云南民族學院學報，2002，11（1）：536，539

Skillfully solving the problem of random sampling numbers by using the model of placing balls into cells

GAO Shan

（School of Mathematics and Statistics，Fuyang Normal University，Fuyang 236037，China）

The models of placing balls into cells and random sampling numbers are two important classical models in probability theory，the model of random sampling numbers can be changed into the model of placing balls into cells．The magic effect of placing balls into cells in solving the problems of random sampling numbers was explained by giving some examples．This method is visual，easy for students to understand，conducive to improve the teaching effect and stimulate students′ interest in learning.

placing balls into cells；random sampling number；probability problem

O211.1∶G642.0

A

10.3969/j.issn.1007-9831.2020.11.019

1007-9831（2020）11-0098-03

2020-03-11

安徽省高等學校省級質量工程項目（2018kfk067）——精品線下開放課程：概率論與數理統計；阜陽師范大學品牌專業建設項目（2019PPZY01）；阜陽師范大學基礎教育研究成果培育項目（2017JCJY13）

高珊（1975-），女，山東汶上人，教授，博士，從事排隊論及可靠性研究．E-mail：sgao_09@yeah.net