基于通用變鄰域搜索的多AGV分揀調度優化

郭超 陳香玲 郭鵬 王強

摘 要：為了解決物流倉儲分揀中心多臺AGV處理大量包裹調度優化困難的問題，在考慮分揀作業時間窗和充電需求的基礎上，研究了大規模AGV調度問題。以最小化分揀作業周期為目標，提出了一種通用變鄰域搜索（general variable neighborhood search，GVNS）算法，為各臺AGV指定轉運任務和作業排序，采用遍歷插入啟發式策略生成滿足時間窗約束的初始解，設計了10種鄰域算子對初始解迭代尋優，并對比不同規模算例的算法性能，分析AGV充電速率和數量配置對分揀效率的影響。結果表明，GVNS算法具有計算時間和求解性能方面的優勢，能在較短時間內求得近似最優解，平均計算時間僅為532.78 s，明顯優于混合整數規劃模型和約束規劃模型;當包裹數為100時，最合適的AGV配置為14輛。因此，GVNS可以有效解決分揀中心考慮充電需求和硬時間窗的大規模多AGV調度問題，提高物流分揀效率，幫助企業找到科學、合理的AGV配置方案。

關鍵詞：物流系統管理;分揀作業;自動導引小車;調度;充電需求;變鄰域搜索

中圖分類號：F252.1;TP301?? 文獻標識碼：A

doi：10.7535/hbkd.2021yx05011

收稿日期：2021-08-20;修回日期：2021-09-19;責任編輯：張士瑩

基金項目：國家重點研發計劃項目（2020YFB1712200）;宜賓職業技術學院科研平臺建設計劃資助項目（YBZY21KYPT-03）;軌道交通運維技術與裝備四川省重點實驗室開放課題（2020YW004）

第一作者簡介：郭 超（1984—），男，四川宜賓人，講師，主要從事智能制造方面的研究。

通訊作者：郭 鵬副教授。E-mail：pengguo318@swjtu.edu.cn

General variable neighborhood search for the multi-AGV scheduling problem with sorting operations

GUO Chao1，2，CHEN Xiangling3，GUO Peng1，3，WANG Qiang2

（1.Technology and Equipment of Rail Transit Operation and Maintenance Key Laboratory of Sichuan Province，Chengdu，Sichuan 610031，China;2.School of Intelligent Manufacturing，Yibin Vocational and Technical College，Yibin，Sichuan 644003，China;3.School of Mechanical Engineering，Southwest Jiaotong University，Chengdu，Sichuan 610031，China）

Abstract：To solve the intractable multiple automatic guided vehicles （AGVs） scheduling problem encountered in the sorting processes of the logistics sorting centers，a large-scale AGV scheduling problem was studied on the basis of considering the sorting time windows and charging requirements.A general variable neighborhood search （GVNS） algorithm was proposed to minimize the makespan of the sorting operations，in which the assignment of transferring packages to AGVs and the sequence of sorting tasks for each AGV were determined.The traversal insertion heuristic was developed to generate the initial solution of the developed algorithm to ensure the constraint of time windows.Ten neighborhood operators were designed to optimize the initial solution for the iteration of the algorithm.Different sized test instances were compared，and the impacts of AGV charging rate and quantity configuration on sorting efficiency were analyzed.The results show that the GVNS algorithm is superior in computing time and solution performance.It can obtain the approximate optimal solution in a short time.The average computing time of GVNS is only 532.78 s，which is obviously better than the mixed integer and constraint programming models;when the number of packages is 100，the most suitable number of AGVs is 14.Therefore，GVNS can effectively solve the large-scale and multi-AGV scheduling problem with charging demand and hard time window，improve the efficiency of logistics sorting，and help enterprises find the scientific and reasonable AGV configuration scheme.

Keywords：

logistics system management;sorting operation;automatic guided vehicle;scheduling;charging demand;vari-able neighborhood search

隨著電子商務產業的不斷發展壯大，中國快遞包裹經歷了連續十多年的爆炸式增長，從2010年的不足24億件迅速攀升到2020年的833.6億件，目前快遞總量已超過美國、日本及歐洲發達國家的快遞量總和，成為名副其實的“快遞大國”。逐年增長的快遞業務量對高效配送提出了更高要求。快遞包裹從賣家手中到達買家手中需要經歷一系列步驟，包括訂單確認，快遞攬件、轉運、分揀、運輸，再分揀、轉運與送達等。在完整的快遞配送流程中，至少要經歷2次分揀，且每次分揀均會耗費大量時間。因此，提高物流中心的分揀效率，可以在一定程度上縮短快遞整體配送時間，讓買家在更短時間內收到包裹。為了應對暴增的業務量，原有的人工分揀或傳送帶式倉儲物流相繼被自動導引車（automatic guided vehicle，AGV）或自主移動機器人（autonomous mobile robot，AMR）揀選作業系統替代。各大快遞公司（包括菜鳥、申通、順豐等）相繼引入了類似于亞馬遜Kiva機器人（見圖1）的作業系統[1-2]。采用上述分揀系統能夠實現無人化、自動化與智能化，但面臨的管理決策也更加復雜。因此，對多臺機器人開展調度優化成為物流機器人領域研究的熱點問題之一。早期AGV在單個項目或者場景中應用尚可，但其依賴于磁條等固定導航方式，只能在作業區域內按照固定的路徑循環運行，應用相對簡單，且不需要系統具備較高的調度能力。類Kiva機器人的出現，使得對多AMR集群調度的需求越來越大[3]。多AMR調度除了要為每個AMR合理分配任務從而達到預期目標，還要考慮到任務時間窗、優先級、充電需求等各種限制因素。在倉儲物流中，AMR或者AGV調度主要依賴于最短隊列或最短走行距離等啟發式規則進行決策[4]。為了實現對AGV集群調度的優化，人們提出了多種元啟發式算法，包括粒子群-遺傳混合算法[5]、差分進化算法[6]、Memetic算法[7]、大規模鄰域搜索[8]、自適應大規模鄰域搜索[9]等。但這些研究對于實際場景中的柵格地圖和充電約束等考慮尚不充分，缺乏有效的求解手段。為了分析AGV調度規則，仿真手段也被用于調度分析和對比中[10]。

變鄰域搜索（variable neighborhood search，VNS）算法具有良好的通用性和尋優能力，已在調度、設施布局、設施選址、車輛路徑等問題中取得了良好效果[11-17]。然而目前還鮮有文獻報道使用VNS解決考慮充電需求和時間窗的多AGV調度問題。為實現對大規模問題實例的求解，筆者基于文獻[18]的研究工作，在多AGV調度優化建模基礎上提出采用通用變鄰域搜索（general variable neighborhood search，GVNS）算法，針對多AGV作業場景下的分揀調度優化問題，設計了一種啟發式規則，為通用變鄰域搜索算法提供初始解，采用10個不同的鄰域結構用于局部搜索和擾動階段，分析AGV充電速率和數量配置對優化目標的影響，通過算例測試，驗證了算法的求解性能。

1 物流分揀流程

圍繞分揀作業流程，物流分揀中心分為入庫區、出庫區和分揀區3部分。分揀區由分揀臺、投放口和設備充電/停放區組成，如圖2所示，其中a和b分別代表柵格的行數和列數。在分揀區內，來自不同地區的包裹入庫后隨著傳送帶到達各個分揀臺，AGV接收到搬運任務后前往包裹所在分揀臺。AGV到達分揀臺后需要根據包裹上的運單信息，將包裹運送至相應的投放口，每個投放口代表不同的城市或地區。在投放口的下方是漏斗和傳送帶，它們會收集包裹并將其運送至出庫區，在出庫區會有車輛進行下一階段的配送。

基于以上應用場景，給定任務集合J={1，2，…，n}，其中J為包含所有任務的集合，n為任務總數。給定AGV集合K={1，2，…，m}，其中K為所有AGV集合，m為其數量（m=|K|）。AGV不工作時均停靠在充電區，當接收到分揀作業指令時，其從充電區出發執行分揀任務。每個包裹i（i∈J）都有相應的最早到達時間ei、搬運時間ti和最晚完工時間di，最晚完工時間用于保證包裹分揀出庫后的準時派送。

AGV在運送包裹時需經歷3個階段：1）從當前位置前往包裹所在的分揀臺;2）若AGV在ei之前到達分揀臺，則需等待，否則直接裝載包裹;3）AGV運送包裹到對應的投放口。每運送完一個包裹，AGV會檢查當前電量是否低于安全電量g。當電量充足時，AGV直接前往下一包裹所在分揀臺;當電量不足時，其需前往充電區充電，充電完成后再去到下一個包裹所在分揀臺。如此反復，直至所有運輸任務執行完畢，最后返回充電區。具體描述與數學規劃模型詳見文獻[18]。

2 GVNS算法的主要步驟及鄰域結構

變鄰域搜索算法在應用過程中衍生處理諸多拓展算法，包括變鄰域深度搜索算法、變鄰域分解搜索算法和偏態變鄰域搜索算法等[19-20]。本文所提出的通用變鄰域搜索（GVNS）是在局部搜索階段采用VND的變鄰域搜索算法，相比其他的VNS拓展算法擁有非常優秀的求解性能，目前已被用于求解單分配集線器定位[21]、帶時間窗約束的多目標車輛路徑與裝載[22]和取送貨一體的旅行商[23]等復雜組合優化問題。GVNS算法的基本思想是在搜索過程中通過變換不同的操作算子盡可能多地探索解空間，尋找局部最優解，然后通過擾動跳出局部最優，經過多次迭代，不斷更新最優解直至達到終止條件。

2.1 編碼方式

采用由整數構成的編碼列表來表示每輛AGV待執行的任務序列，其中每個整數表示AGV需要搬運的包裹編號。每個AGV必須從充電區出發，在執行完所有的任務后返回充電區。

因此每個AGV的編碼列表首尾位置都設置為0，分別表示虛擬開始任務和虛擬結束任務。所有AGV的編碼列表即為問題的一個解。如圖3所示，以10個包裹3輛AGV為例，其中包裹[1，3，10]由第1輛AGV負責搬運，包裹[5，2，8，4]由第2輛AGV搬運，同理，包裹[6，9，7]由第3輛AGV負責搬運，共計3條路徑列表構成了一個完整的解。

由圖3可以看出，在編碼階段并沒有將充電任務加入到任務列表中，這是為了便于后續的鄰域操作。對于是否需要執行充電任務，會在遍歷AGV的每條路徑時加以判斷，進而獲得目標函數值。

2.2 初始解

初始解的質量會影響整個算法的求解效率。為了找到較好的初始可行解，設計了一種啟發式方法，其偽代碼算法如表1所示。

首先生成m個僅包含虛擬開始任務和虛擬結束任務的空路徑[0，0];然后遍歷所有任務，計算每個任務在每條路徑的每個位置的適應度值，同時記錄下每個任務的適應度值和對應的插入位置;找到擁有最小適應度值的任務后，將該任務插入此位置，然后從任務列表中刪除該任務;遍歷完所有的任務并全部插入到路徑列表后，輸出初始解。表1中步驟8的適應度值計算公式為

f=α×Cmax+（1-α）（s′i-si），i∈N。

式中：Cmax為分揀完成時間;點i為路徑中插入點后面的點;si為點i在插入前的路徑中的開始時間;s0為點i在插入后路徑中的開始時間。對權重α進行取值，使初始可行解盡可能地實現最小化分揀完成時間和時間窗更緊湊，得到不錯的初始解。

2.3 鄰域結構

GVNS算法涉及10個不同的操作算子。為了便于后續操作，為每個操作算子進行標號處理。需要特別說明的是，每種操作算子在選擇任務節點時都不會選擇位于路徑首尾位置的虛擬開始任務點和虛擬結束任務點。常用的操作算子包括Cross，2-opt，Relocate，Exchang和ICross，各自操作方式如下。

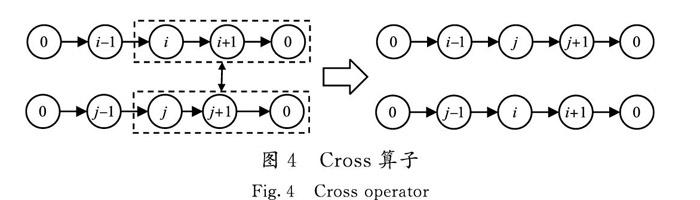
1）Cross算子（N1） 選擇任意2條路徑，分別從2條路徑任選1個點作為路徑的斷點，然后交換2條路徑的后半段，形成2條新的路徑，操作示例見圖4。

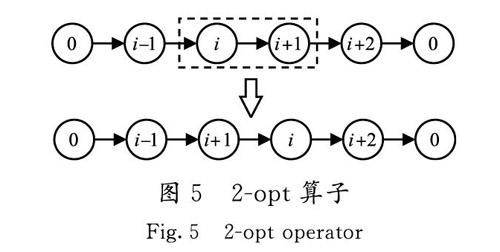
2）2-opt算子（N2） 選擇任意1條路徑，在該路徑中選擇2個不同的點作為斷點，使得路徑形成3個片段，然后對中間片段進行逆序操作，形成1條新的路徑，操作示例見圖5。

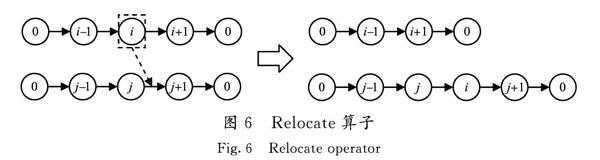
3）Relocate算子（N3） 重新定位結構，是指任意選擇2條路徑，從1條路徑中任意選擇1個點插入到另1條路徑的任意位置，形成2條新的路徑，操作示例見圖6。

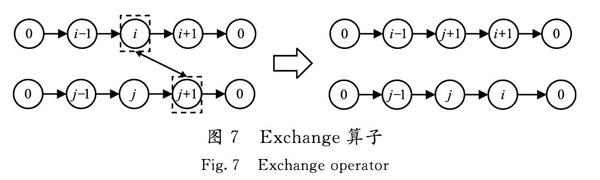
4）Exchange算子（N4） 選擇任意2條路徑，分別從2條路徑中選擇1個點進行交換，操作示例見圖7。

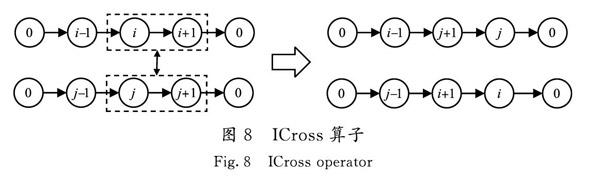
5）ICross算子（N5） 選擇任意2條路徑，分別取2條路徑任意長度的中間片段，將2條路徑的中間片段進行逆序操作然后交換，形成2條新的路徑，操作示例見圖8。

此外，為了擴大鄰域解的解空間，還使用了Or-opt算子、GENI算子、λ-Interchange算子3種擴展鄰域結構[24]，通過多次迭代保證對最優解的搜索能力。

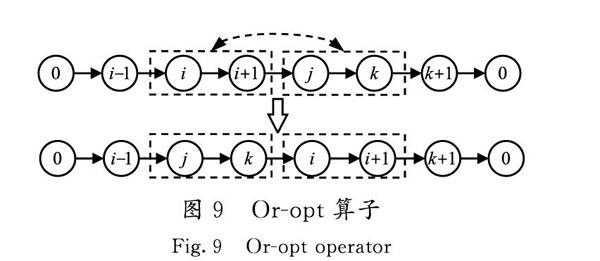
Or-opt算子（N6， N7，N8）：從任意1條路徑中隨機選擇1個點i，然后選擇1個距離i點給定長度x的點j（j=i+x），再從路徑中隨機選擇1個點k。路徑被i，j，k 3個點截成4個片段，如果k<i或k>j，則交換路徑的2個中間片段的位置，從而形成1條新路徑。通過為該算子設置3個不同長度參數x（x=1，2，3），形成了3個不同的鄰域結構。當x=2且k>j時，操作過程如圖9所示。

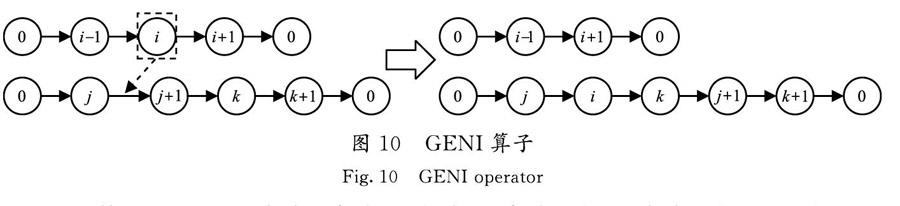
GENI算子（N9）：選擇任意2條路徑，從第1條路徑中選擇1個點i插入第2條路徑中的任一位置，然后從第2條路徑中選擇1個點k插入i點后面，形成2條新路徑，操作示例見圖10。

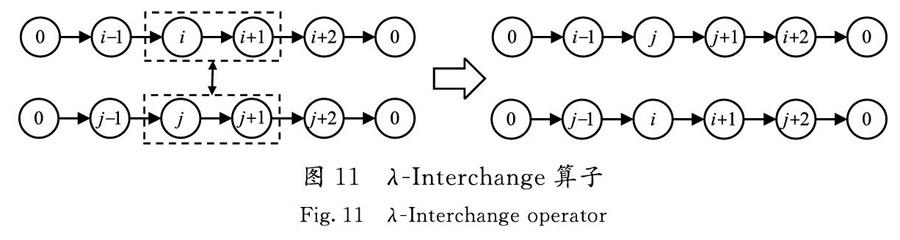
λ-Interchange算子（N10）：選擇任意2條路徑，分別從2條路徑中選擇任意一點隨機長度為λ1和λ2的片段進行交換，形成2條新的路徑。若路徑1的長度為l1，選定點的位置為a，路徑2的長度為l2，選定點的位置為b，則λ1和λ2分別從整數均勻分布[1，l1-a-1]和[1，l2-b-1]中隨機選擇。當λ1=λ2=2時，操作示例如圖11所示。

2.4 局部搜索階段

令Nl（l=1，2，…，lmax）為一組用于局部搜索階段的鄰域結構集合，令Nl（s）為當前解s在第l個鄰域結構中的解集合。采用上述10個鄰域結構（lmax=10）構成VND獲得鄰域解集。基于文獻[19]的算法機制，局部搜索階段從鄰域N1開始，到鄰域N10結束。將當前解s傳入一個鄰域結構后會產生一組鄰域解Nl（s），其中必然存在一個局部最優解s′。若該局部最優解s′優于當前解s，則將s替換為s′，并且返回到第一個鄰域結構進行搜索;否則，進入下一個鄰域結構進行搜索，直到搜索完最后一個鄰域，若仍未能找到更優解，則結束局部搜索階段。VND算法流程偽代碼如表2所示。

2.5 擾動階段

局部搜索階段容易使算法陷入局部最優。當多次迭代仍然無法對解進行改善時，通常可對當前解進行適當的擾動操作，生成下一次進入局部搜索階段的起始解。若當前解在經過連續η次迭代后仍未能找到更優，則說明算法陷入了局部最優，沒有必要繼續進行局部搜索，需要對當前解進行擾動操作。令Nk（k=1，2，…，kmax）為一組用于擾動階段的鄰域結構集合，令Nk（s）為當前解s在第k個鄰域結構中的解集合，該階段同樣是上述的10個鄰域結構（kmax=10）。為了使解空間得到有效擴展，選擇隨機生成10個鄰域結構的搜索順序。每次擾動操作時，只需選擇一個操作算子，與局部搜索階段不同的是，操作算子隨機選擇路徑和節點進行操作，而不是遍歷，當找到一個可行解時即可結束擾動階段。

2.6 算法框架

GVNS算法流程如表3所示，GVNS在定義了鄰域結構Nk和Nl后（第1行），利用啟發式規則生成初始解s0，并將其傳遞給當前解s（第2行），然后進行初始化操作（第3行）。隨后開始迭代搜索，在擾動階段找到一個可行解s′后（第5行），帶著該可行解s′進入局部搜索階段（第6行）。在局部搜索階段，通過目標函數值的大小評價解的質量。目標函數值越小，表示解的質量越好。如果找到的局部最優解s″優于可行解s′，則將s′替換為s″。結束局部搜索階段后，需要判斷找到的局部最優解s′是否優于當前解s （第7行）。如果是，則將s替換為s′，并且依然使用擾動階段定義的第一個鄰域結構進行擾動操作（第8行），否則進一步判斷是否繼續進行迭代搜索。如果達到算法終止條件，則返回當前最優解s （第10—17行）。算法的終止條件為當前解連續Inip次迭代仍未能得到改善（第11行），若滿足該條件，則立即終止算法并輸出當前最優解。在GVNS算法中，設置Inip=10。需要特別說明的是，達到最大未優化迭代次數Inip是指連續擾動了Inip次，且每次擾動后都會經歷局部搜索階段，但當前解都未得到改善。

3 算例分析

通過一系列的算例數值實驗驗證所提出的GVNS算法的性能，算法由Python語言實現，在配置為AMD Ryzen 5-4600U with Radeon Graphics CPU @ 2.10 GHz，16.0 GB的個人電腦上運行。為了對比所提出GVNS算法的性能，文獻[11]中提到的混合整數規劃（mixed integer programming，MIP）模型和約束規劃（constraint programming，CP）模型也被用于求解算例。在算例分析中，MIP采用Gurobi求解器求解，CP采用CPLEX Optimization Studio 12.10.0中的CP Optimizer求解。引入相對百分比偏差（relative percentage difference，RPD）分析算法的性能，RPD計算公式如下：

RPD=Ccurrent-CbestCbest×100%。（2）

式中：Ccurrent表示當前方法求得的目標值，Cbest為該算例在所有方法中取得的最優目標值。RPD值越小，表示該方法求解效果越好。

3.1 算例設計

算例生成采用文獻[11]所述方法，分為小規模算例和大規模算例。針對小規模算例，設置包裹數n={8，10，14};針對大規模算例，設置包裹數n={50，100，200}。表4為算例中包裹數與AGV數的關系，可以得到18組不同規模的算例，每組隨機生成4個算例，共計72個。

3.2 參數調試

參數設置會直接影響算法效果，不同權重α取值的Rinit均值圖見圖12。在本文所提的GVNS算法中，權重α作為唯一變量需要進行參數調試。在此，考慮不同的取值水平：0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1。選擇包裹數n=50，AGV數m取值{5，6，7，8，9，10，11，12，13，14，15}的11個大規模算例來調試權重α的取值。

權重α只會影響初始解，因此需觀察初始解目標函數值的大小。為了簡化數據量，取所有算例在某一α值下初始解目標函數值的平均值Rinit，Rinit值越小，表示初始解的質量越好。由圖12可知，每個α的取值點均對應參數測試算例集的平均值;從圖12中還可以看出，當α為0.9時，Rinit值最小，因此設置權重α值為0.9。

3.3 計算結果與分析

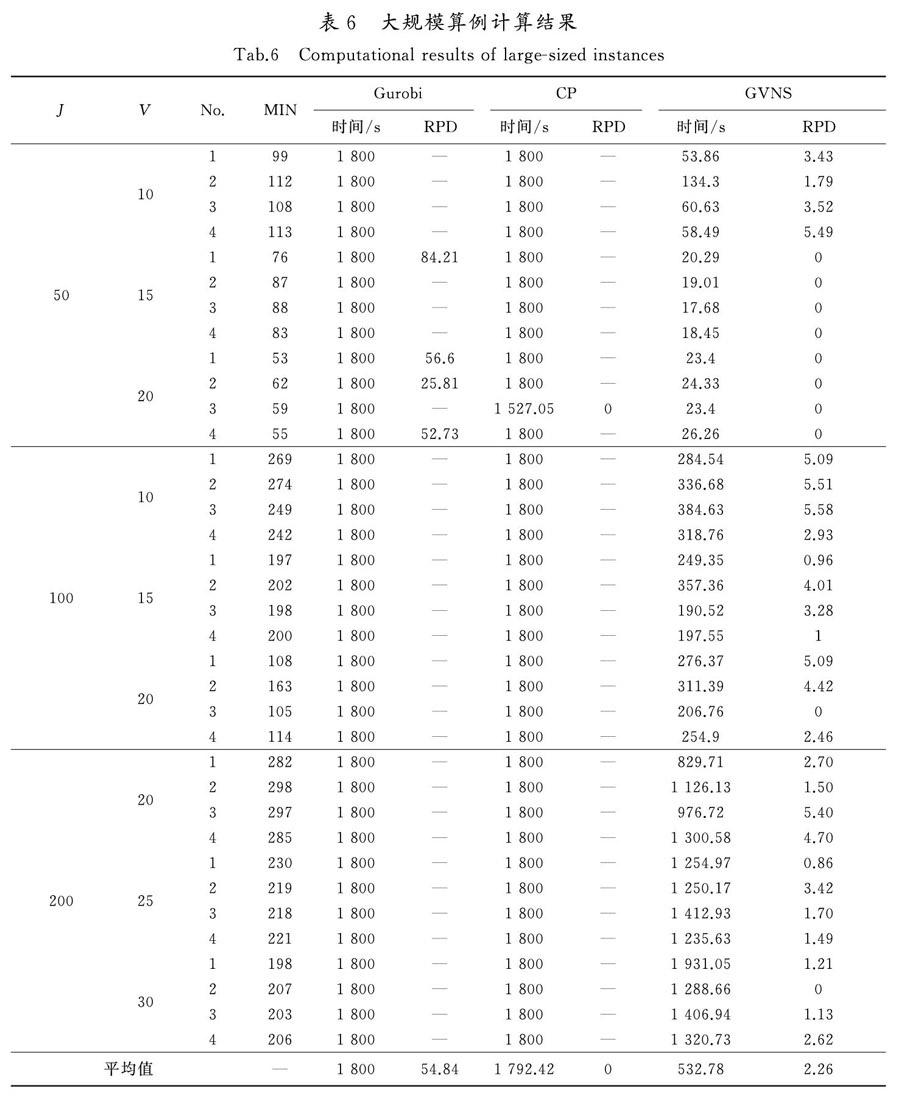
將Gurobi和CP Optimizer的最大求解時間設置為1 800 s，若在給定時間內未找到最優解，則停止計算并返回當前的最好可行解。GVNS算法的求解性能用RPD值進行評價，此外，計算時間也作為求解性能評價指標。為了消除啟發式算法可能存在的隨機性影響，GVNS算法對每個算例計算10次，然后取平均計算時間和平均RPD值。表5給出了小規模算例的計算結果，大規模算例的計算結果如表6所示，其中“J”表示包裹數量，“V”表示AGV數量，“No.”表示該組算例序號，“MIN”表示該算例求得的最小目標函數值，“—”表示未在規定時間內找到可行解。每個方法均列出了計算時間和RPD，對比小規模算例和大規模算例分別在MIP模型、CP模型和GVNS算法中的計算結果。

從表5可以看出，與啟發式方法相比，精確算法仍存在明顯的差距。MIP模型有8個算例未能找到最優解，CP模型有9個算例未能找到最優解，而GVNS僅有1個算例未能找到最優解。從計算時間上來看，GVNS平均計算時間僅為0.42 s，遠小于MIP和CP的計算時間。從求解質量上來看，GVNS的平均RPD值僅為0.09，也遠小于另外2個模型的RPD值。由小規模算例計算結果可知，GVNS在計算時間和求解質量上都具有明顯優勢。

由表6可知，由于本問題的NP-hard特性，當包裹數為50時，MIP模型和CP模型還有部分算例能找到最優解或近似解，但當包裹數達到100及以上時，MIP模型和CP模型在所有算例中均無法在1 800 s內找到可行解，可見優化求解器無法求解大規模問題。而GVNS在所有大規模算例中均能在較短時間內求得近似最優解，平均計算時間僅為532.78 s，明顯優于MIP模型和CP模型。由此可知，GVNS可以有效解決分揀中心考慮充電需求和硬時間窗的大規模多AGV調度問題。

3.4 AGV配置分析

不同配置的AGV會有不同的充電速率，配置越高充電率越大，即充電速度越快。不同的AGV充電率會導致AGV充電所需時間不同，從而影響分揀完成時間。此外，在一定分揀作業量下，不同AGV數量配置同樣會影響分揀完成時間。對于企業而言，AGV的配置越高，采購成本就越高，但如果AGV的配置過低，又會導致分揀任務無法按時完成或分揀效率過低。因此，找到合適的AGV充電率配置和數量配置對于物流中心來說是非常有必要的。本文以包裹數n=100，AGV數m=10的算例來分析不同的AGV充電率對分揀完成時間的影響。以包裹數n=100，AGV數m={10，12，14，16，18，20}的算例來分析AGV數量對分揀完成時間的影響。由于算例規模較大，因此使用GVNS算法進行求解。為了簡化數據量，同時消除算法隨機性帶來的影響，每個算例都要計算10次，然后取分揀完成時間的平均值。

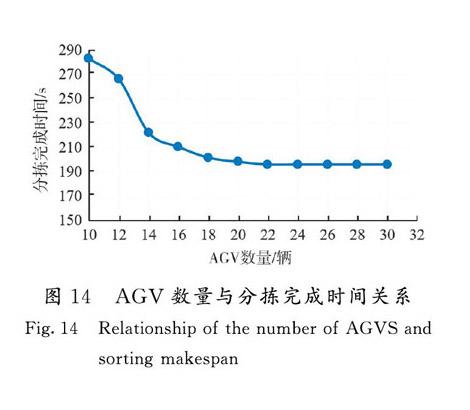
圖13為不同的AGV充電率與分揀完成時間關系折線圖。從圖13可以看出，當充電率大于1.6時，分揀完成時間不再明顯減少，因此當包裹數為100，AGV數為10時，最合適的AGV充電率為1.6。圖14是不同AGV數量配置與分揀完成時間關系折線圖。由圖14可知，當AGV數量大于22時，分揀完成時間不再發生變化。因此，當包裹數為100時，最多只需配置22輛AGV。當AGV數量大于14時，分揀完成時間不再明顯減少，因此，當包裹數為100時，最合適的AGV數量配置為14輛。

4 結 語

1）為了提高物流分揀中心的作業效率，在考慮充電需求和時間窗約束的基礎上，研究了大規模作業場景下的多AGV調度優化問題。

2）基于所研究問題的復雜性，提出利用GVNS實現對大規模算例的有效求解。在GVNS算法的基本框架下，結合問題特性，設計了滿足時間窗約束的啟發式方法生成初始解，并為算法設計了10個鄰域操作算子，生成局部最優解。

3）使用不同規模的算例進行數值實驗，并與混合整數規劃模型和約束規劃模型進行對比，計算結果驗證了所提出的GVNS算法求解大規模問題的可行性和高效性。考慮到不同的AGV充電率和數量配置會影響多AGV的調度方案，采用控制變量法分別分析了不同的AGV充電率和數量配置下的分揀完成時間，并給出了合理的配置方案。

本文僅考慮分揀中心有一個充電區的情況，在實際應用場景中，當分揀場地很大且AGV數量很多時，AGV需要頻繁地返回充電區充電，合理的充電區布局方案是一個值得深入研究的問題。實際AGV分揀過程中還有很多問題需要考慮，例如AGV充電和放電的規律、AGV速度變化和AGV故障停機等。目前有關此方面的研究數據尚未見公開報道，筆者也在嘗試通過實驗獲得真實的運行數據，以使所討論的算法更具實際應用價值。此外，在未來的研究中，還可通過仿真分析探討更多的不確定情況，譬如單個AGV的意外故障或包裹的緊急分揀作業等;同時還需對諸如遺傳算法、自適應大規模鄰域搜索等算法之間的性能進行對比分析的相關工作。

參考文獻/References：

[1] WEIDINGER F，BOYSEN N，BRISKORN D.Storage assignment with rack-moving mobile robots in KIVA warehouses[J].Transportation Science，2018，52（6）：1297-1588.

[2] 沈博聞，于寧波，劉景泰.倉儲物流機器人集群的智能調度和路徑規劃[J].智能系統學報，2014，9（6）：659-664.

SHEN Bowen，YU Ningbo，LIU Jingtai.Intelligent scheduling and path planning of warehouse mobile robots[J].CAAI Transactions on Intelligent Systems，2014，9（6）：659-664.

[3] FRAGAPANE G，de KOSTER R，SGARBOSSA F，et al.Planning and control of autonomous mobile robots for intralogistics：Literature review and research agenda[J].European Journal of Operational Research，2021，294（2）：405-426.

[4] da COSTABARROS? R，NASCIMENTO T P.Robotic mobile fulfillment systems：A survey on recent developments and research opportunities[J].Robotics and Autonomous Systems，2021，137：103729.

[5] 岳笑含，許曉健，王溪波.面向FMS基于改進的混合PSO-GA的多AGV調度算法研究[J].計算機科學，2018，45（Z2）：167-171.

YUE Xiaohan，XU Xiaojian，WANG Xibo.Research on muti-AGV sechduling algorithm based on improved hybrid PSO-GA for FMS[J].Computer Science，2018，45（Z2）：167-171.

[6] 余娜娜，李鐵克，王柏琳，等.自動化分揀倉庫中多AGV調度與路徑規劃算法[J].計算機集成制造系統，2020，26（1）：171-180.

YU Nana，LI Tieke，WANG Bailin，et al.Multi-AGVs scheduling and path planning algorithm in automated sorting warehouse[J].Com-puter Integrated Manufacturing Systems，2020，26（1）：171-180.

[7] JUN S，LEE S，YIH Y.Pickup and delivery problem with recharging for material handling systems utilising autonomous mobile robots[J].European Journal of Operational Research，2021，289（3）：1153-1168.

[8] POLTEN L，EMDE S.Scheduling automated guided vehicles in very narrow aisle warehouses[J].Omega，2021，99：102204.

[9] ULJ I，SALEWSKI H，GOEKE D，et al.Order batching and batch sequencing in an AMR-assisted picker-to-parts system[J].European Journal of Operational Research，2021.doi：10.1016/j.ejor.2021.05.033.

[10]陳敏，黎展滔，陳慶新，等.考慮有限物流運輸能力的智能車間AGV調度算法研究[J].工業工程，2019，22（4）：49-57.

CHEN Min，LI Zhantao，CHEN Qingxin，et al.AGV scheduling algorithm of intelligent workshop considering limited logistics transportation capacity[J].Industrial Engineering Journal，2019，22（4）：49-57.

[11]陳香玲，郭鵬，溫昆，等.考慮充電需求和時間窗的多AGV調度優化建模[J].河北科技大學學報，2021，42（2）：91-100.

CHEN Xiangling，GUO Peng，WEN Kun，et al.Optimized mathematical models for multi-AGV scheduling problem with charging requirements and time windows[J].Journal of Hebei University of Science and Technology，2021，42（2）：91-100.

[12]范厚明，劉鵬程，吳嘉鑫，等.集貨需求隨機的同時配集貨VRP及混合變鄰域搜索算法[J].系統工程理論與實踐，2019，39（10）：2646-2659.

FAN Houming，LIU Pengcheng，WU Jiaxin，et al.Hybrid genetic algorithm with variable neighborhood descent for the vehicle routing problem with simultaneous stochastic pickup and deterministic delivery[J].Systems Engineering：Theory & Practice，2019，39（10）：2646-2659.

[13]WU X Q，CHE A.Energy-efficient no-wait permutation flow shop scheduling by adaptive multi-objective variable neighborhood search[J].Omega，2020，94：102117.

[14]徐立云，程贊，宓宏，等.基于改進變鄰域搜索算法的成型機分批重調度優化[J].同濟大學學報（自然科學版），2020，48（10）：1460-1469.

XU Liyun，CHENG Zan，MI Hong，et al.Molding machines batch rescheduling optimization based on improved variable neighborhood search[J].Journal of Tongji University（Natural Science），2020，48（10）：1460-1469.

[15]CUI L Q，LIU X B，LU S J，et al.A variable neighborhood search approach for the resource-constrained multi-project collaborative scheduling problem[J].Applied Soft Computing，2021，107：107480.

[16]HERRN A，MANUEL C J，DUARTE A.An efficient variable neighborhood search for the space-free multi-row facility layout problem[J].European Journal of Operational Research，2021，295（3）：893-907.

[17]HOOGERVORST R，DOLLEVOET T，MARTI G，et al.A variable neighborhood search heuristic for rolling stock rescheduling[J].EURO Journal on Transportation and Logistics，2021，10：100032.

[18]SADATI M E H，ATAY B.A hybrid variable neighborhood search approach for the multi-depot green vehicle routing problem[J].Transportation Research Part E：Logistics and Transportation Review，2021，149：102293.

[19]MLADENOVI N，HANSEN P.Variable neighborhood search[J].Computers & Operations Research，1997，24（11）：1097-1100.

[20]董紅宇，黃敏，王興偉，等.變鄰域搜索算法綜述[J].控制工程，2009，16（sup2）：1-5.

DONG Hongyu，HUANG Min，WANG Xingwei，et al.Review of variable neighborhood search algorithm[J].Control Engineering of China，2009，16（sup2）：1-5.

[21]MIKI M，TODOSIJEVI R，UROEVI D.Less is more：General variable neighborhood search for the capacitated modular hub location problem[J].Computers & Operations Research，2019，110：101-115.

[22]SONG X，JONES D，ASGARI N，et al.Multi-objective vehicle routing and loading with time window constraints： A real-life application[J].Annals of Operations Research，2020，291（1）：799-825.

[23]MLADENOVI N，UROEVI D，HANAFI S，et al.A general variable neighborhood search for the one-commodity pickup-and-delivery travelling salesman problem[J].European Journal of Operational Research，2012，220（1）：270-285.

[24]de ARMAS J，MELIN-BATISTA B，MORENO-PREZ J A，et al.GVNS for a real-world rich vehicle routing problem with time windows[J].Engineering Applications of Artificial Intelligence，2015，42：45-56.